6.6: Орбітальний кутовий момент і P-орбіталі
- Page ID
- 27350
- Пов'язати класичний орбітальний момент моменту для частинки з квантовим еквівалентом
- Охарактеризувати мангітуду та орієнтацію орбітального моменту для електрона через квантові числа
Класичний орбітальний кутовий момент
Фізична величина, відома як момент імпульсу, відіграє домінуючу роль у розумінні електронної структури атомів. Щоб отримати фізичну картину і відчути кутовий момент, необхідно розглянути модельну систему з класичної точки зору. Найпростішою класичною моделлю атома водню є така, в якій електрон рухається по круговій орбіті з постійною швидкістю або кутовою швидкістю (Рисунок Template:index). Подібно до того, як лінійний імпульс\(m\vec{v}\) відіграє домінуючу роль при аналізі лінійного руху, так і кутовий імпульс (\(L\)) відіграє центральну роль в аналізі системи з круговим рухом, як це знайдено в моделі атома водню.
На малюнку Template:index,\(m\) це маса електрона,\(\vec{v}\) лінійна швидкість (швидкість, якою володів електрон, якби він продовжував рухатися по дотичній до орбіти) і\(r\) радіус орбіти. Лінійна швидкість\(\vec{v}\) є вектором, оскільки вона має в будь-який момент як величину, так і напрямок у просторі. Очевидно, що при обертанні електрона на орбіті напрямок постійно\(\vec{v}\) змінюється, і, таким чином, лінійний імпульс не\(m\vec{v}\) є постійним для кругового руху. Це так навіть при тому, що швидкість електрона (тобто величина\(\vec{v}\) якого позначається\(|\vec{v}|\)) залишається незмінною. Згідно з другим законом Ньютона, сила повинна діяти на електрон, якщо його імпульс змінюється з часом. Це сила, яка заважає електрону літати по дотичній до його орбіти. В атомі сила притягання, яка містить електрон, - це електростатична сила тяжіння між ядром і електроном, спрямована вздовж радіуса r під прямим кутом до напрямку руху електрона.
Кутовий момент, як і лінійний імпульс, є вектором і визначається наступним чином:
\[|\vec{L}| = m \nu r \nonumber \]
Кутовий момент імпульсу вектора або\(\vec{L}\) спрямований уздовж осі обертання. З визначення видно, що вектор кутового моменту залишатиметься постійним до тих пір, поки швидкість електрона на орбіті буде постійною t (\(|\vec{v}|\)пере магістраль незмінною), а площина і радіус орбіти залишаються незмінними. Таким чином, для даної орбіти кутовий момент є постійним до тих пір, поки кутова швидкість частинки на орбіті постійна. В атомі єдина сила на електроні на орбіті спрямована вздовж g\(r\); вона не має складової в напрямку руху. Сила діє таким чином, щоб змінити тільки лінійний імпульс. Тому, хоча імпульс вух лінії не є постійним під час кругового руху, кутовий імпульс є. Сила, що діє на частинку у напрямку вектора,\(\vec{v}\) змінила б кутову швидкість і кутовий імпульс. Коли застосовується сила, яка робить cha nge\(\vec{L}\), крутний момент, як кажуть, діє на систему. Таким чином, кутовий імпульс і крутний момент пов'язані так само, як і лінійний імпульс і сила.
Квантовий кутовий імпульс
Важливим моментом вищевикладеного обговорення є те, що і кутовий імпульс, і енергія атома залишаються постійними, якщо атом залишається непорушеним. Будь-яка фізична величина, яка є постійною в класичній системі, як зберігається, так і квантується в квантово-механічній системі. Таким чином, і енергія, і момент імпульсу квантуються для атома.
Будь-яка фізична величина, яка є постійною в класичній системі, як зберігається, так і квантується в квантово-механічній системі.
Існує квантове число, що позначається\(l\), яке регулює величину моменту моменту, точно так само, як квантове число\(n\) визначає енергію. Величина моменту моменту може припускати тільки ті значення, які задаються:
\[ |L| = \sqrt{l(l+1)} \hbar \label{4} \]
с\(l = 0, 1, 2, 3, ... n-1\).
Крім того, значення n обмежує максимальне значення моменту моменту моменту, оскільки значення l не може бути більшим за n - 1. Для стану n = 1, розглянутого вище,\(l\) може мати значення тільки нуль. Коли n = 2, l може дорівнювати 0 або 1, а для n = 3, l = 0 або 1 або 2 і т.д. коли l = 0, з Рівняння видно,\(\ref{4}\) що кутовий момент електрона дорівнює нулю. Атомні орбіталі, які описують ці стани нульового моменту моменту, називаються орбіталями. S орбіталі відрізняються один від одного шляхом постановки значення n, основного квантового числа. Вони називаються атомними орбіталями 1 s, 2 s, 3 s тощо.
Попереднє обговорення стосувалося 1-ї орбіти, оскільки для основного стану атома водню\(n = 1\) і\(l = 0\). Ця орбітальна і всі орбіталі в цілому прогнозують сферичні розподіли щільності для електрона, як обговорювалося раніше.
Загальноприйнято називати електрон «в» орбіталі, хоча орбітальна є, але математична функція без фізичної реальності. Сказати, що електрон знаходиться в певній орбіталі, означає, що електрон знаходиться в квантовому стані, який описується цією орбіталлю. Наприклад, коли електрон знаходиться в орбіталі 2 с, атом водню знаходиться в стані, для якого\(n = 2\) і\(l = 0\).
Порівнюючи ці результати з результатами для 1 s орбіталі на рисунку Template:index, ми бачимо, що\(n\) при збільшенні середнього значення\(r\) збільшень. Це погоджується з тим, що енергія електрона також\(n\) збільшується зі збільшенням. Підвищена енергія призводить до того, що електрон в середньому відтягується далі від привабливої сили ядра. Як і в простому прикладі електрона, що рухається по прямій, в розподілах ймовірностей з'являються вузли (значення\(r\) для яких електронна щільність дорівнює нулю). Кількість вузлів збільшується зі збільшенням енергії і дорівнює\(n - 1\).
Коли електрон має кутовий імпульс, розподіли щільності більше не сферичні. Фактично для кожного значення\(l\) розподіл електронної густини приймає характерні форми на рисунку Template:index.
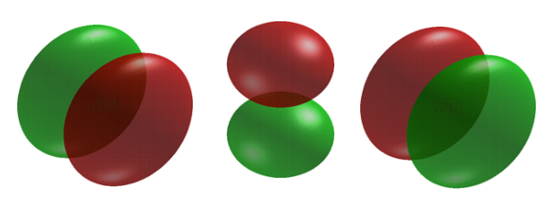
Коли\(l = 1\), орбіталі називаються p орбіталями. При цьому орбіта і її електронна щільність концентруються уздовж лінії (осі) в просторі. Орбітальна або хвильова функція 2 р позитивна за значенням з одного боку і негативна за значенням на іншій стороні площини, яка перпендикулярна осі орбіти і проходить через ядро. Орбіталь має вузол в цій площині, і, отже, електрон в орбіталі 2 р не розміщує жодної електронної щільності заряду в ядрі. Електронна щільність орбіти 1 с, з іншого боку, є максимумом в ядрі. Така ж діаграма для розподілу щільності 2 р отримана для будь-якої площини, яка містить цю вісь. Таким чином, у трьох вимірах електронна щільність, здається, зосереджена у двох частках, по одній на кожній стороні ядра, причому кожна частка має кругову форму в поперечному перерізі Рисунок Template:index.
Електрон володіє орбітальним моментом, має розподіли щільності більше не сферичні.
\(m_l\)Квантове число та магнітні поля
Магнітне квантове число, позначене літерою\(m_l\), є третім квантовим числом, які описують унікальний квантовий стан електрона. Магнітне квантове число відрізняє орбіталі, наявні в підоболонці, і використовується для обчислення азимутальної складової орієнтації орбіти в просторі. Як і при нашому обговоренні жорстких роторів, квантове число\(m_l\) відноситься до проекції кутового моменту в цьому довільно обраному напрямку, умовно званому\(z\) напрямком або віссю квантування. \(L_z\), Величина моменту моменту в напрямку z, задається за формулою
\[ L_z = m_l \hbar \nonumber \]
Квантове число\(m_l\) відноситься, нещільно, до напрямку вектора моменту моменту. Магнітне квантове число впливає\(m_l\) лише на енергію електрона, якщо він знаходиться в магнітному полі, оскільки за відсутності одного всі сферичні гармоніки, відповідні різним довільним значенням,\(m_l\) еквівалентні. Магнітне квантове число визначає зсув енергії атомної орбіти за рахунок зовнішнього магнітного поля (це називається ефектом Зеемана) - звідси і назва магнітного квантового числа. Однак фактичний магнітний дипольний момент електрона в атомній орбіталі надходить не тільки від електронного кутового імпульсу, але і від електронного спіна, вираженого в спінового квантового числа, яке є четвертим квантовим числом. \(m_s\)і обговорюється в наступному розділі.
Відповідь складна; хоча\(m_l=0\) відповідає\(p_z\), орбіталі для\(m_l=+1\) і\(m_l=−1\) лежать в xy-площині (див. Сферичні гармоніки), але не на осях. Причиною такого результату є те, що хвильові функції зазвичай формулюються у сферичних координатах, щоб полегшити математику, але графіки в декартових координатах мають більш інтуїтивний сенс для людини. \(p_y\)Орбіталі\(p_x\) і будуються за допомогою лінійного комбінованого підходу з радіальних і кутових хвильових функцій і перетворюються в\(xy\) (про це йшлося раніше). Таким чином, неможливо безпосередньо співвіднести значення з\(m_l=±1\) конкретними орбіталями. Поняття про те, що ми можемо це зробити, іноді представлено на вступних курсах, щоб зробити складну математичну модель трохи простішою та інтуїтивнішою, але вона невірна.
Три хвильові функції для\(n=2\) і\(l=1\) такі.
\[ \begin{align} |\psi_{2,1,0} \rangle &=r \cos θR(r) \\[4pt] |\psi_{2,1,+1} \rangle &=−\dfrac{r}{2} \sinθ e^{iϕ} R(r) \\[4pt] |\psi_{2,1,-1} \rangle &=+\dfrac{r}{2} \sinθ e^{-iϕ} R(r) \end{align} \nonumber \]
Позначення\(R(r)\) є\(|\psi_{n,l,m_l} \rangle\) з - радіальна складова цієї хвильової фукції,\(θ\) є кутом по відношенню до осі z і\(ϕ\) є кутом по відношенню до\(xz\) -площині.
\[R(r)=\sqrt{\dfrac{Z^5}{32\pi a_0^5}}\mathrm{e}^{-Zr/2a_0} \nonumber \]
в якому\(Z\) знаходиться атомний номер (або, можливо, краще ядерний заряд) і\(a_0\) є радіусом Бора.
При переході від сферичних до декартових координат ми робимо підстановку\(z=r \cosθ\), так:
\[|\psi_{2,1,0} \rangle =z R(r) \nonumber \]
Це пов'язано\(\psi_{2p_z}\) з тим,\(\psi \) що значення залежить від\(z\): when\(z=0\);\(\psi =0\), що очікується, оскільки\(z=0\) описує\(xy\) -plane.
Інші дві хвильові функції вироджуються в\(xy\) -площині. Еквівалентне твердження полягає в тому, що ці дві орбіталі не лежать на осях x і y, а скоріше бісекціонують їх. Таким чином, типово приймати лінійні комбінації з них, щоб рівняння виглядало красивіше. Якщо будь-який набір хвильових функцій є розв'язком рівняння Шредінгера, то будь-який набір лінійних комбінацій цих хвильових функцій також повинен бути розв'язком (Розділ 2.4). Ми можемо зробити це через лінійність рівняння Шредінгера.
У рівняннях нижче, ми збираємося використовувати деякі тригонометрії, зокрема формулу Ейлера:
\[ \begin{align} \mathrm{e}^{\mathrm{i}\phi} &=\cos{\phi}+\mathrm{i}\sin{\phi}\\[4pt] \sin{\phi} &= \dfrac{\mathrm{e}^{\mathrm{i}\phi}-\mathrm{e}^{-\mathrm{i}\phi}}{2\mathrm{i}}\\[4pt] \cos{\phi} &= \dfrac{\mathrm{e}^{\mathrm{i}\phi}+\mathrm{e}^{-\mathrm{i}\phi}}{2} \end{align} \nonumber \]
Ми також збираємося використовувати\(x=\sin θ\cos ϕ\) і\(y=\sin θ \sinϕ \).
\ почати {вирівнювати*}\ psi_ {2p_x} &=\ dfrac {1} {\ sqrt {2}}\ ліворуч (\ psi_ {2,1, +1} -\ psi_ {2,1, -1}\ праворуч)\\ [4pt] &=\ dfrac {1} {2}\ ліворуч (\ mathrm {e} ^ {\ mathrm {i}\ phi} +\ матхрм {е} ^ {-\ матрм {i}\ фі}\ фі}\ право) r\ sin {\ тета} f (r)\\ [4pt] &= r\ sin {\ тета}\ cos {\ Phi} f (r) = xf (r)\\ [4pt]\ psi_ {2p_y} &=\ dfrac {\ mathr m {i}} {\ sqrt {2}}\ ліворуч (\ psi_ {2,1, +1} +\ psi_ {2,1, -1}\ праворуч)\\ [4pt] &=\ dfrac {1} {2\ mathrm {i}}\ лівий (\ mathrm {e} ^ {i}\ mathrm {i}\ phi} -\ mathrm {i}\ phi}) r\ sin {\ тета} f (r)\\ [4pt] &=r\ sin {\ тета}\ sin {\ phi} f (r) = yf (r)\\\ end {align*}
Отже, в той час як\(m_l=0\) відповідає\(|p_z \rangle\),\(m_l=+1\) і\(m_l=−1\) не може бути безпосередньо призначений ні для\(|p_x \rangle\) одного або\(|p_y \rangle\), а скоріше поєднання\(|p_x \rangle\) і\(|p_y \rangle\). Альтернативним описом є те, що\(m_l=+1\) може відповідати\((|p_x \rangle\ + |p_y \rangle )\) і\(m_l=−1\) може відповідати\((|p_x \rangle\ - |p_y \rangle)\).
D-орбіталі (ще вищі хвильові функції кутових моментів)
Коли орбіталі називаються d орбіталями\(l = 2\), а Figure Template:index показує контури в площині для 3 d орбіталі та її розподіл щільності. Зверніть увагу, що щільність знову дорівнює нулю в ядрі і що зараз є два вузли в орбіталі та в її розподілі щільності. Зі збільшенням моменту імпульсу електрона розподіл щільності стає все більш концентрованим вздовж осі або в площині в просторі. Тільки електрони на\(s\) орбіталах з нульовим моментом дають сферичні розподіли щільності і додатково розміщують щільність заряду в положенні ядра.
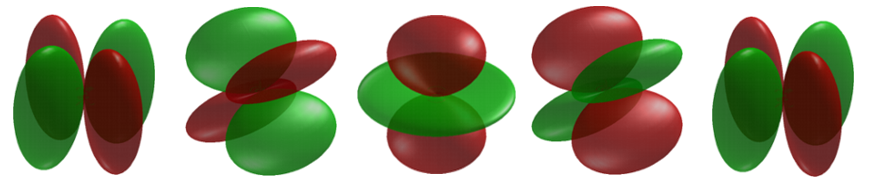
Як і у випадку з p-орбіталями, єдиною d-орбіталлю, яку\(m_l\) можна приписувати специфічним, є\(d_{z^2}\) орбіталі с\(m_l=0\). Решта - лінійні комбінації хвильових функцій атома водню зі складними сферичними гармонійними кутовими компонентами.
Здається, немає ні рими, ні причини для іменування станів, відповідних різним значенням\(\ell\) (s, p, d, f для l = 0, 1, 2, 3). Цей набір етикеток мав свій початок на ранніх роботах експериментальної атомної спектроскопії. Буква s позначала гострий, p для основного, d для дифузного і f для фундаментального в характеристиці спектральних ліній. Від літери f і далі іменування орбіталів є алфавітним \(l = 4,5,6 \rightarrow g,h,i, ....\).
Ми ще не врахували повного виродження орбіталей атома водню, які ми заявляли раніше\(n^2\) для кожного значення\(n\). Наприклад, коли\(n = 2\), існує чотири різних атомних орбіталі. Решта виродження знову визначається кутовим моментом системи. Оскільки кутовий імпульс, як лінійний імпульс, є векторною величиною, ми можемо звернутися до компонента вектора кутового імпульсу, який лежить уздовж певної обраної осі. З причин, які ми будемо досліджувати, кількість значень, які конкретний компонент може прийняти для заданого значення\(l\) is (\(2l + 1\)). Таким чином\(l = 0\), коли, немає моменту імпульсу і є лише одна орбітальна, і s орбітальна. Коли\(l = 1\) існує три можливі значення для компонента (\(2 \times 1 + 1\)) загального моменту моменту, які фізично відрізняються один від одного. Отже, існує три p орбіталі. Аналогічно існує п'ять орбіталів d, (\(2 \times 2+1\)), сім орбіталів f, (\(2 \times 3 +1\)) тощо Усі орбіталі з однаковим значенням\(n\) і\(l\), наприклад, три орбіталі 2p схожі, але відрізняються за своєю просторовою орієнтацією.
Щоб краще зрозуміти цей кінцевий елемент виродження, ми повинні більш детально розглянути, що прогнозує квантова механіка щодо кутового моменту електрона в атомі.
Дописувачі та атрибуція
- Template:ContribZielinski
- Template:ContribBader
- Stack Exchange (Ben Norris and Loong)