10.4: Ентропія електрохімічних клітин

Last updated
Save as PDF

Page ID: 21093

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Функція Гіббса пов'язана з ентропією через її температурну залежність

\[ \left( \dfrac{\partial \Delta G}{\partial T} \right)_p = - \Delta S\]

Аналогічну залежність можна вивести і для температурної дисперсії\(E^o\).

\[ nF \left( \dfrac{\partial E^o}{\partial T} \right)_p = \Delta S \label{eq2}\]

Розглянемо наступні дані для клітини Даніеля (Buckbeei, Surdzial, & Metz, 1969), що визначається наступною реакцією

\[Zn(s) + Cu^{2+}(aq) \rightleftharpoons Zn^{2+}(aq) + Cu(s)\]

Т (°C)	0	10	20	25	30	40
Ео (V)	1.1028	1.0971	1.0929	1.0913	1.0901	1.0887

Від прилягання даних до квадратичної функції, температурна залежність

\[\left( \dfrac{\partial E^o}{\partial T} \right)_p \]

легко встановлюється.

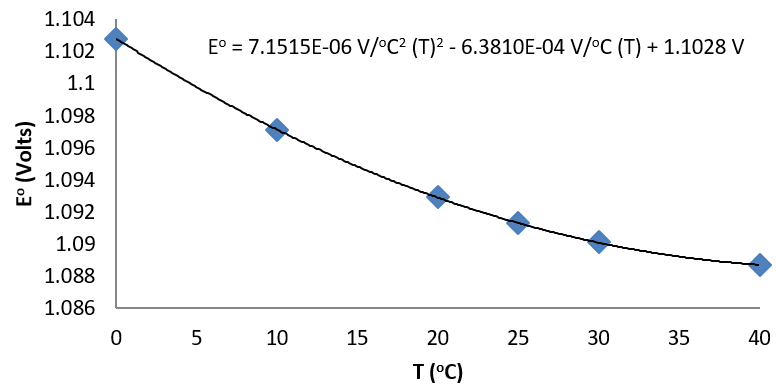
Малюнок\(\PageIndex{1}\): Температурна залежність потенціалу клітини для клітини Даніеля.

Квадратичне прилягання до даних призводить до

\[\left( \dfrac{\partial E^o}{\partial T} \right)_p = 3.8576 \times 10^{-6} \dfrac{V}{°C^2}(T) - 6.3810 \times 10^{-4} \dfrac{V}{°C}\]

Так, при 25° С

\[\left( \dfrac{\partial E^o}{\partial T} \right)_p = -54166 \times 10^{-4} V/K\]

зазначивши, що\(K\) можна замінити,\(°C\) так як в різниці вони мають однакову величину. Отже, зміна ентропії обчислюється (Equation\ ref {eq2})

\[ \Delta S = nF \left( \dfrac{\partial E^o}{\partial T} \right)_p = (2\,mol)(95484\,C/mol) (-5.4166 \times 10^{-4} V/K)\]

Тому що

\[ 1\,C \times 1\,V = 1\,J\]

Стандартна зміна ентропії для клітинної реакції Даніеля при 25° C становить

\[ \Delta S = -104.5\, J/(mol\,K).\]

Саме негативна зміна ентропії призводить до збільшення стандартного потенціалу клітин при більш низьких температурах. Для такої реакції, як

\[Pb(s) + 2 H^+(aq) \rightarrow Pb^{2+}(aq) + H_2(g)\]

що має велике збільшення ентропії (за рахунок вироблення газофазного продукту), стандартний потенціал осередку зменшується зі зниженням температури. Оскільки це реакція, яка використовується в більшості автомобільних акумуляторів, це пояснює, чому може бути важко запустити автомобіль дуже холодним зимовим ранком. Тема температурної залежності декількох стандартних потенціалів комірок повідомляється і обговорюється Bratsch (Bratsch, 1989).