2.7: Реальні гази
- Page ID
- 21055
Хоча ідеального закону газу достатньо для прогнозування великої кількості властивостей та поведінки газів, є кілька разів, що відхилення від ідеальності надзвичайно важливі.
Рівняння ван дер Ваальса
Запропоновано декілька рівнянь стану для обліку відхилень від ідеальності. Одним з простих, але корисних виразів є те, що запропонував Йоганнес Дідерік ван дер Ваальс (1837 — 1923) (Йоганнес Дідерік ван дер Ваальс - Біографічний, 2014)

Рівняння ван дер Ваальса ввів поправки до тиску та об'єму закону ідеального газу з метою обліку міжмолекулярних взаємодій та розміру молекул відповідно.
\[ \left ( p + \dfrac{a}{V_m^2} \right) (V_m - b) = RT \label{vdw}\]
або
\[ p =\dfrac{RT}{V_m-b} - \dfrac{a}{V_m^2} \label{vdw2}\]
У цьому виразі\(a\) і\(b\) є змінними даної речовини, які можуть бути виміряні і табличні. Взагалі, молекули з великими міжмолекулярними силами матимуть великі значення\(a\), а великі молекули матимуть великі значення b\(\PageIndex{1}\).
| Газова частота зіткнень | а (атм Л 2 моль-2) | b (л/моль) |
|---|---|---|
| Він | 0.0341 | 0.0238 |
| N 2 | 1.352 | 0.0387 |
| СО 2 | 3.610 | 0.0429 |
| С 2 Ч 4 | 4.552 | 0.0305 |
Модель Ван дер Уоллс корисна тим, що дозволяє так просто інтерпретувати параметри з точки зору молекулярних розмірів і міжмолекулярних сил. Але він також має обмеження (як у випадку з кожною науковою моделлю!) Деякі інші корисні двопараметричні та трипараметричні (або більше) рівняння стану включають моделі Редліха-Квонга, Дітеріка та Клаузіуса (Таблиця\(\PageIndex{2}\)). Вони мають ту перевагу, що дозволяють залежати від температури від деяких параметрів, що, як буде видно пізніше, необхідно для моделювання певної поведінки реальних газів.
| Модель | Рівняння стану |
|---|---|
| Ідеальний | \(p = \dfrac{RT}{V_m}\) |
| ван дер Ваальс (ван дер Ваальс Дж., 1967) | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{V_m^2}\) |
| Редліх-Квонг (Редліх і Квонг, 1949) | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{\sqrt{T} V_m (V_m +b)}\) |
| Дієтичні (Дієтичні, 1899) | \( p =\dfrac{RT}{V_m-b} \exp \left( \dfrac{-a}{V_mRT} \right)\) |
| Клаузіус | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{T (V_m + c)^2}\) |
| Віріальні рівняння | \( p =\dfrac{RT}{V_m} \left(1+ \dfrac{B(T)}{V_m} +\dfrac{C(T)}{V_m} \dots \right) \) |
Віріальне рівняння
Дуже зручним виразом, що дозволяє відхилення від ідеальної поведінки, є Віріальне рівняння стану. Це просте розширення силового ряду, в якому терміни вищого порядку містять всі відхилення від ідеального закону газу.
\[ p =\dfrac{RT}{V_m} \left(1+ \dfrac{B(T)}{V_m} +\dfrac{C(T)}{V_m} \dots \right ) \label{viral}\]
У межі, що B (T) (Другий віріальний коефіцієнт) і C (T) дорівнюють нулю, рівняння стає ідеальним газовим законом. Також молярний обсяг газів невеликий, зменшуються за величиною внески з третього, четвертого і т.д., дозволяючи обрізати ряд в зручній точці. Другий віріальний коефіцієнт можна передбачити з теоретичної міжмолекулярної потенційної функції за допомогою
\[B(T) = N_a \int _{r=0}^{\infty} \left[ 1- \exp \left(\dfrac{U(r)}{k_BT} \right) \right] 2\pi r^2 \,dr\]
Якість міжмолекулярного потенціалу може бути визначено (частково) здатністю потенціалу прогнозувати значення другого віріального коефіцієнта,\(B(T)\).
Потенціал Леонарда-Джонса
Функція міжмолекулярного потенціалу використовується для опису взаємодій між молекулами. Ці взаємодії повинні включати привабливі сили, які будуть зводити молекули разом, і сили відштовхування, які розштовхують їх. Якщо молекули являють собою тверді сфери, позбавлені будь-яких привабливих взаємодій, потенційна функція досить проста.
\[ U(r) ={\begin{cases} \infty &{\text{for }}r\leq \sigma\\0&{\text{for }}r>\sigma.\end{cases}}\]
У цій функції\(\sigma\) визначається розмір молекул. Якщо дві молекули потрапляють на відстані одна\(r\) від одної, вони стикаються, відскакуючи при ідеально пружному зіткненні. Реальні молекули, однак, мають діапазон міжмолекулярних поділів, завдяки яким вони будуть відчувати сили привабливості (так звана «м'яка стінка» потенційної поверхні.) І тоді при дуже малих поділах будуть домінувати сили відштовхування, розсуваючи молекули в сторони (так звана «тверда стінка» потенційної поверхні.)
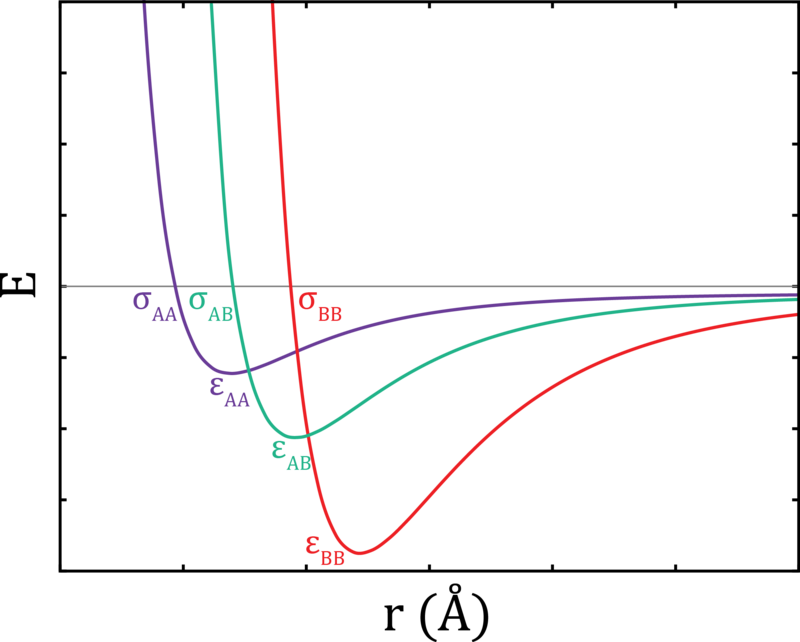
Зазвичай використовуваним міжмолекулярним\(U(r)\) потенціалом є потенціал Леонарда-Джонса. Ця функція має вигляд
\[ U(r) = 4 \epsilon \left[ \underbrace{\left(\dfrac{\sigma}{r}\right)^{12}}_{\text{repulsive term}} - \underbrace{\left(\dfrac{\sigma}{r}\right)^{6}}_{\text{attractive term}} \right] \]
де\(\sigma\) регулює ширину потенційної свердловини, і\(\epsilon\) регулює глибину. Відстань між молекулами задається\(r\). Відразливі взаємодії між молекулами містяться в перших членах, а привабливі взаємодії виявляються у другому семестрі.
Розширення серії Тейлор
Загальноприйнятим методом створення силового ряду на основі іншого рівняння є розширення серії Тейлора. Це розширення функції про корисну контрольну точку, де кожен з членів генерується шляхом диференціації вихідної функції.
Для функції ряд\(f(x)\) Тейлора\(F(x)\) може бути згенерований з виразу
\[F(x) = f(a) + \left.\dfrac{d}{dx} f(x) \right|_{x=a} (x-a) + \dfrac{1}{2!} \left. \dfrac{d^2}{dx^2} f(x) \right|_{x=a} (x-a)^2 + \dots\]
Це може бути застосовано до будь-якого рівняння стану, щоб вивести вираз для віріальних коефіцієнтів через параметри рівняння стану.
Застосування до рівняння ван дер Ваальса
Рівняння ван дер Ваальса можна записати через молярний об'єм (Equation\ ref {vdw2}). При множенні правого боку на\(\frac{u}{u}\) (де\(u = 1/v\)) виходить:
\[ p =\dfrac{RTu}{1-bu} - au^2\]
Цей вираз може бути «Talyor» розширено (до перших трьох членів) про\(u = 0\) (що відповідає нескінченному молярному об'єму.) Терміни коефіцієнта, які потрібні для розширення, є
\[p(u=0)=0\]
\[ \dfrac{dp}{du} \big|_{u=0} = \left [ \dfrac{RT}{1-bu} + \dfrac{bRTu}{(1-bu)^2} - 2au \right]_{u=0} = RT\]
\[ \dfrac{d^2p}{du^2} \big|_{u=0} = \dfrac{1}{2} \left [ \dfrac{bRT}{(1-bu)^2} + \dfrac{bRT}{(1-bu)^2} - \dfrac{2b^2RTu}{(1-bu)^3} - 2au \right]_{u=0} = RT -a\]
\[ \dfrac{d^3p}{du^3} \big|_{u=0} = RTb^2\]
А віріальне рівняння потім можна виразити через параметри ван дер Ваальса як
\[ p = 0 +RT(u) + (bRT -a)(u)^2 + RTb^{2(u)^3}\]
Підстановка\(u = 1/V\) і спрощення дає бажаний результат:
\[ p= RT \left[ \dfrac{1}{V} + \dfrac{b-\frac{a}{RT}}{V^2} + \dfrac{b^2}{V^3} + \dots \right]\]
А другий віріальний коефіцієнт задається
\[ B(T) = b-\dfrac{a}{RT}\]
Температура Бойла
Корисним способом вираження відхилень від ідеальності є визначення коефіцієнта стиснення (\(Z\)), заданого
\[ Z = \dfrac{pV_m}{RT}\]
де\(V_m\) - молярний обсяг. Для ідеального газу,\(Z = 1\) під всі комбінації\(P\)\(V_m\), і\(T\). Однак реальні гази показуватимуть деяке відхилення (хоча всі гази наближаються до ідеальної поведінки при низькому p, високому V m та високому T). Коефіцієнт стиснення азоту при декількох температурах показаний нижче в діапазоні тисків.

Як видно, газ поводиться ближче до ідеалу в більш тривалому діапазоні тиску при більш високих температурах. Загалом, існує одна температура, температура Бойла, при якій газ наближається до ідеальної поведінки, оскільки тиск асимптотично йде до нуля, і, таким чином, вести себе ідеально в широкому діапазоні нижчих тисків. Температура Бойла знаходить шляхом вирішення
\[ \lim_{p \rightarrow 0} \left( \dfrac{\partial Z}{\partial p} \right) = 0\]
або
\[ \lim_{1/V_m \rightarrow 0} \left( \dfrac{\partial Z}{\partial \left(\frac{1}{V_m} \right)} \right) = 0\]
Використовуючи віріальне рівняння стану (Equation\ ref {viral}), температуру Бойла можна виразити через віріальні коефіцієнти. Починаючи з коефіцієнта стиснення
\[Z = 1 +\dfrac{B}{V_m} + \dots\]
а потім диференціювання щодо\(1/V_m\) врожайності
\[\dfrac{\partial Z}{\partial \left(\frac{1}{V_m}\right)} = B\]
Так що можна зробити висновок, що при температурі Бойля другий віріальний коефіцієнт\(B\) дорівнює нулю. Це повинно мати певний сенс, враховуючи, що перший віріальний коефіцієнт забезпечує більшу частину відхилення від ідеального закону газу, і тому він повинен зникнути, оскільки газ поводиться більш ідеально.
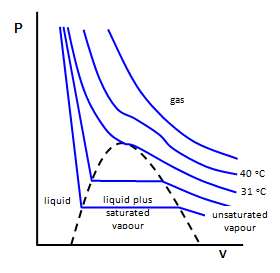
Критична поведінка
Ізотерми (лінії постійної температури) СО 2 виявляють дуже велике відхилення від ідеальної поведінки. При високих температурах СО 2 поводиться відповідно до закону Бойла. Однак при більш низьких температурах газ починає конденсуватися, утворюючи рідину при високих тисках. При одній конкретній температурі, критичній температурі, ізотерма починає відображати цю критичну поведінку. Температура, тиск і молярний об'єм (\(p_c\),\(T_c\), і\(V_c\)) в цій точці визначають критичну точку. Для вирішення виразів для критичних констант потрібно три рівняння. Рівняння стану забезпечує одне співвідношення. Другу можна генерувати, визнаючи, що нахил ізотерми в критичній точці дорівнює нулю. І нарешті, третій вираз виводиться шляхом визнання того, що ізотерма проходить через точку перегину в критичній точці. Використовуючи рівняння ван дер Ваальса як приклад, ці три рівняння можуть бути згенеровані наступним чином:
Розв'язування цих виразів для\(p_c\)\(T_c\), і\(V_c\) дає
\[p_c = \dfrac{a}{27b^2}\]
\[T_c = \dfrac{8a}{27bR}\]
\[V_c = 3b\]
Критичні змінні можуть бути використані таким чином для визначення значень молекулярних параметрів, що використовуються в рівнянні стану (наприклад, рівняння ван дер Ваальса) для даної речовини.
Принцип відповідних держав
Принцип відповідних держав був запропонований ван дер Ваальсом в 1913 році (van der Waals J.D., 1913). Він зазначив, що коефіцієнт стиснення в критичній точці
\[Z_c = \dfrac{p_cV_c}{RT_c}\]
дуже майже те ж саме для будь-якої речовини. Це узгоджується з тим, що передбачається рівнянням ван дер Ваальса, яке пророкує\(Z_c = 0.375\) незалежно від речовини.
Далі можна відзначити, що на основі зменшених змінних визначаються
\[p_r= \dfrac{p}{p_c}\]
\[V_r= \dfrac{V}{V_c}\]
\[T_r= \dfrac{T}{T_c}\]
Виявлено, що кілька фізичних властивостей можна порівняти з реальними речовинами. Наприклад (Гуггенхайм, 1945), для аргону, криптону, азоту, кисню, вуглекислого газу та метану знижена стисливість становить
\[[ \dfrac{p_cV_c}{RT_c} \approx 0.292\]
Також знижений коефіцієнт стиснення може бути позначений як функція зниженого тиску для декількох речовин при декількох відновлених ізотермах з дивовижною консистенцією незалежно від речовини:
