6.2: Орбіталі

Хартрі Опис

Вважається, що енергії та хвильові функції в межах найбільш часто використовуваних теорій атомної структури виникають як розв'язки рівняння Шредінгера, гамільтоніан$h_e(r)$ якого має три види енергій:

1. Кінетична енергія, середнє значення якої обчислюється шляхом прийняття очікуваного значення оператора$-\dfrac{\hbar^2}{2m} \nabla^2$ кінетичної енергії щодо будь-якого конкретного рішення$\phi_j(r)$ рівняння Шредінгера: $$KE = \langle\phi_j| -\dfrac{\hbar^2}{2m} \nabla^2 |\phi_j\rangle$$
2. Куломбічна енергія тяжіння з ядром заряду$Z$: $$\langle\phi_j| -\dfrac{Z_e^2}{r} |\phi_j\rangle$$
3. Кулонівські енергії відштовхування з усіма$N-1$ іншими електронами, які, як передбачається, займають інші атомні орбіталі (AoS) позначаються$\phi_K$, причому ця енергія обчислюється як

$$\sum_K \langle\phi_j(r) \phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle.\label{6.1.2}$$

Позначення Дірака$\langle\phi_j(r) \phi_K(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle$ використовується для представлення шестивимірного інтеграла Кулона

$$J_{J,K} = \int |\phi_j(r)|^2 |\phi_K(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \label{6.1.3}$$

що описує кулонівське відштовхування між щільністю заряду$|\phi_j(r)|^2$ для електрона в$\phi_j$ і щільністю заряду$|\phi_K(r’)|^2$ для електрона в$\phi_K$. Звичайно, сума над$K$ повинна бути обмежена, щоб виключити,$K=J$ щоб уникнути підрахунку «самовзаємодії» електрона в орбіталі$\phi_j$ з самим собою.

Загальна енергія$\epsilon_J$ орбіти$\phi_j$, являє собою суму вищевказаних трьох внесків:

$$\epsilon_J = \langle\phi_j| - \frac{\hbar^2}{2m} \nabla^2 |\phi_j\rangle + \langle\phi_j| -\frac{Z_e^2}{r} |\phi_j\rangle + \sum_K \langle\phi_j(r) \phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle.\label{6.1.4}$$

Ця обробка електронів та їх орбіталів називається рівнем теорії Хартрі. Як зазначено вище, коли екрановані гідрогенні АО використовуються для наближення$\phi_j$ та$\phi_K$ орбіталей, результуючі$\epsilon_J$ значення не дають точних прогнозів. Наприклад, негатив$\epsilon_J$ повинен наближатися до енергії іонізації для видалення електрона з АТ$\phi_j$. Такі потенціали іонізації (ІС) можуть бути виміряні, а виміряні значення погано узгоджуються з теоретичними значеннями, коли робиться наближення грубого скринінгу для АТ.

Розширення LCAO

Для вдосконалення використання екранованих гідрогенних AoS найбільш часто наближається кожен з Hartree AoS {$\phi_K$} як лінійну комбінацію так званих базисних AoS {$\chi_\mu$}:

$$\phi_J = \sum_\mu C_{J,\mu} \chi_\mu.\label{6.1.5}$$

використовуючи те, що називається розширенням лінійної комбінації атомних орбіталів (LCAO). У цьому рівнянні коефіцієнти розширення {$C_{J,\mu}$} - це змінні, які повинні бути визначені шляхом розв'язання рівняння Шредінгера

$$h_e \phi_J = \epsilon_J \phi_J. \label{6.1.6}$$

Підставивши розширення LCAO для$\phi_J$ цього рівняння Шредінгера, помноживши зліва на одну з базисних AoS$\chi_\nu$, а потім інтегруючи над координатами електрона в$\phi_J$, отримуємо

$$\sum_\mu \langle\chi_\nu| h_e| \chi_\mu\rangle C_{J,\mu} = \epsilon_J \sum_\mu \langle\chi_\nu| \chi_\mu\rangle C_{J,\mu} . \label{6.1.7}$$

Це матричне рівняння власних значень, в якому$\epsilon_J$ і {$C_{J,\mu}$} відображаються як власні значення та власні вектори. Матриці$\langle\chi_\nu| h_e| \chi_\mu\rangle$ і$\langle\chi_\nu| \chi_\mu\rangle$ називаються гамільтонових і перекриваються матрицями відповідно. Явний вираз для першого виходить при введенні більш раннього визначення he:

$$\langle\chi_\nu| h_e| \chi_\mu\rangle = \langle\chi_\nu| - \frac{\hbar^2}{2m} \nabla^2 |\chi_\mu\rangle + \langle\chi_\nu| -\frac{Ze^2}{r} |\chi_\mu\rangle \label{6.1.8}$$

$$+ \sum_{\eta,\gamma} \sum_K C_{K,\eta} C_{K,\gamma} \langle\chi_\nu(r) \chi_\eta(r’) |\frac{e^2}{|r-r’|} | \chi_\mu(r) \chi_\gamma(r’)\rangle. \label{6.1.9}$$

Важливим моментом, на який слід звернути увагу на форму матричних рівнянь Хартрі, є те, що для обчислення гамільтонової матриці потрібно знати коефіцієнти LCAO {$C_{K,\gamma}$} орбіталів, які займають електрони. З іншого боку, ці коефіцієнти LCAO повинні бути знайдені шляхом розв'язання рівнянь власних значень матриці Хартрі. Цей парадокс призводить до необхідності розв'язання цих рівнянь ітераційно в так званій техніці самоузгодженого поля (SCF). У процесі SCF вводять початкове наближення до коефіцієнтів {$C_{K,\gamma}$}. Це дозволяє сформувати гамільтонову матрицю, визначену вище. Матричні рівняння Хартрі

$$\sum_\mu \langle\chi_\nu| h_e| \chi_\mu\rangle C_{J,m} = \epsilon_J \sum_\mu \langle\chi_\nu| \chi_\mu\rangle C_{J,\mu} \label{6.1.10}$$

потім вирішуються для нових {$C_{K,\gamma}$} коефіцієнтів і для орбітальних енергій {$\epsilon_K$}. Нові коефіцієнти LCAO тих орбіталей, які зайняті, потім використовуються для формування нової гамільтонової матриці, після чого рівняння Хартрі знову вирішуються для іншого покоління коефіцієнтів LCAO і орбітальних енергій. Цей процес продовжують до тих пір, поки орбітальні енергії і коефіцієнти LCAO, отримані в послідовних ітераціях, не відрізняються помітно. При такій збіжності можна сказати, що самоузгоджене поле було реалізовано, оскільки коефіцієнти {$C_{K,\gamma}$} використовуються для формування потенціалу кулонівського поля, який деталізує електронно-електронні взаємодії.

Базисні набори

Орбіталі типу Слейтера та орбіталі типу Гауса

Як зазначалося вище, можна використовувати екрановані гідрогенні орбіталі як {$\chi_\mu$}. Однак багато зусиль було витрачено на розробку альтернативних наборів функцій для використання в якості базових орбіталів. Результатом цих зусиль стало створення двох видів функцій, які в даний час широко використовуються. Базові орбіталі, які зазвичай використовуються в процесі LCAO, діляться на два початкові класи:

1. Орбіталі типу Слейтера ( $$c_{n,l,m} (r,\theta,\phi) = N_{n,l,m,z} Y_{l,m} (\theta,\phi) r_{n-1} e^{-zr}$$ STO) характеризуються$n$$l$ квантовими числами$m$ та показниками (які характеризують радіальний розмір орбіти)$z$. Символ$N_{n,l,m,z}$ позначає константу нормалізації.
2. Декартові орбіталі типу Гаусса (ГТО) $$c_{a,b,c} (r,\theta,\phi) = N'_{a,b,c,a} x_a y_b z_c e^{-ar^2}$$ характеризуються квантовими числами$a$$b$, і$c$, які деталізують кутову форму і напрямок орбіти, і експоненти,$a$ які регулюють радіальний розмір.

Для обох типів АО координати$r$$\theta$, і$\phi$ відносяться до положення електрона щодо набору осей, прикріплених до ядра, на якому розташована орбітальна основа. Зверніть увагу, що орбіталі типу Слейтера (STO) схожі на гідрогенні орбіталі в області, близькій до ядра. Зокрема, вони мають ненульовий нахил біля ядра

$$\dfrac{d}{dr}(e^{-zr})_{r=0} = -z.$$

На відміну від цього, GTO, мають нульовий нахил поблизу,$r=0$ оскільки

$$\dfrac{d}{dr}(e^{-ar^2})_{r=0} = 0.$$

Ми говоримо, що STO демонструють стрибок$r=0$, що характерно для гідрогенних розчинів, тоді як ГТО цього не роблять. Хоча STO мають належну поведінку cusp поблизу ядер, вони використовуються в основному для обчислень атомних та лінійних молекул, оскільки багатоцентрові інтеграли

$$\langle\chi_\mu(1) \chi_\kappa(2)|\dfrac{e^2}{|r_1-r_2|}| \chi_\nu(1) \chi_\gamma(2)\rangle\label{6.1.11}$$

які виникають при розрахунках поліатомних молекул (ці інтеграли ми обговоримо пізніше в цій главі) не можуть бути ефективно оцінені при використанні STO. На відміну від цього, такі інтеграли можуть бути зазвичай обчислені при використанні GTO. Ця фундаментальна перевага ГТО призвела до домінування цих функцій у молекулярній квантовій хімії.

Щоб подолати первинну слабкість функцій GTO (тобто їх радіальні похідні зникають у ядрі), прийнято поєднувати два, три або більше ГТО з комбінаційними коефіцієнтами, які фіксуються і не розглядаються як параметри LCAO, у нові функції, які називаються контрактними ГТО (CGTO). Як правило, ряд радіально щільних, середніх і сипучих ГТО множаться на коефіцієнти стиснення і підсумовуються для отримання CGTO, який наближає належний крок в ядерному центрі (хоча жодна така комбінація ГТО не може точно виробляти такий крок, оскільки кожен GTO має нульовий нахил на$r = 0$.

Хоча більшість розрахунків на молекулах зараз виконуються за допомогою гаусових орбіталів, слід зазначити, що інші базові множини можуть бути використані до тих пір, поки вони охоплюють достатню кількість областей простору (радіальних і кутових), де знаходиться значна електронна щільність. Насправді можна використовувати плоскі хвильові орбіталі виду

$$\chi(r,\theta,\phi) = N\exp[i(k_x r \sin{\theta} \cos{\phi} + k_y r \sin_{\theta} \sin{\phi} + k_z r \cos{\theta})],\label{6.1.12}$$

де$N$ є константа нормалізації і$k_x$$k_y$,, і$k_z$ є квантовими числами деталізації моментів або довжини хвилі орбіти уздовж$x$,$y$, і$z$ декартових напрямків. Перевага використання таких простих орбіталів полягає в тому, що інтеграли, які потрібно виконувати, набагато простіше впоратися з такими функціями. Недоліком є те, що потрібно використовувати багато таких функцій для точного опису різко пікових розподілів зарядів, наприклад, внутрішньооболонкових орбіталей ядра, зберігаючи при цьому достатню гнучкість, щоб також описати набагато більш гладку електронну щільність у валентних областях. Багато зусиль було присвячено розробці та складання таблиць у широко доступних місцях наборів базових орбіталів STO або GTO для елементів основної групи та перехідних металів. Ці постійні зусилля спрямовані на забезпечення стандартних базових бібліотек, які:

1. Вихід передбачуваної хімічної точності в результуючих енергіях.
2. Економічно ефективні для використання в практичних розрахунках.
3. Є відносно переносними, так що основа даного атома є достатньо гнучкою, щоб її можна було використовувати для цього атома в різних середовищах зв'язку (наприклад, гібридизація та ступінь іонізації).

Фундаментальне ядро і валентність основи

При побудові атомно-орбітального базису можна вибрати один з декількох класів функцій. По-перше, повинні бути вказані розмір і характер первинного ядра і валентної основи. У межах цієї категорії поширені наступні варіанти:

1. Мінімальна основа, при якій кількість орбіталей CGTO дорівнює числу ядра і валентних атомних орбіталей в атомі.
2. Основа подвійної дзети (DZ), в якій використовується вдвічі більше ЦГТО, ніж є основні та валентні атомні орбіталі. Використання більшої кількості базисних функцій мотивовано бажанням забезпечити додаткову варіаційну гнучкість, тому процес LCAO може генерувати молекулярні орбіталі змінної дифузності, оскільки локальна електронегативність атома змінюється. Валентна подвійна дзета (VDZ) основа має лише один CGTO для представлення орбіталів внутрішньої оболонки, але використовує два набори CGTO для опису валентних орбіталів.
3. Потрійна дзета (TZ) основа, в якій використовується втричі більше ЦГТО, ніж кількість ядра і валентних атомних орбіталей (звичайно, існують також чотирикратние-дзета і вищі дзета-основи). Більш того, існують бази ВТЗ, які обробляють орбіталі внутрішньої оболонки одним CGTO і валентні орбіталі з трьома CGTO.

Оптимізація орбітальних показників (z або a) і коефіцієнтів стиснення GTO-CGTO для описаного вище виду баз зазнала значного зростання в останні роки. Теорічна група в Тихоокеанських північно-західних національних лабораторіях (PNNL) пропонує всесвітній веб-сайт, з якого можна знайти (і навіть завантажити у формі, підготовленій для введення в будь-який з декількох часто використовуваних електронних кодів структури) широкий спектр гаусових атомних базисних наборів. Цей сайт можна отримати тут. Професор Кірк Петерсон з Університету штату Вашингтон бере участь у проекті розвитку базового набору PNNL, але він також проводить свій власний базовий сайт.

Поляризаційні функції

Один зазвичай підсилює будь-який основний і валентний базовий набір з набором так званих поляризаційних функцій. Вони є функціями одного вищого моменту моменту, ніж з'являється в валентному орбітальному просторі атома (наприклад,$d$ -функції для C, N та O та$p$ -функцій для H), і вони мають показники ($z$або$a$), які змушують їх радіальні розміри бути подібними до розмірів валентних орбіталів ( тобто поляризаційні$p$ орбіталі атома Н схожі за розмірами на$1s$ орбітальну, а не$2s$ валентну орбіталь водню). Таким чином, вони не є орбіталями, які описують валентну орбіталь атома з одним більшим l-значенням; такі орбіталі з вищою валентністю l були б радіально більш дифузними.

Основною метою поляризаційних функцій є надання додаткової кутової гнучкості процесу LCAO при формуванні зв'язкових орбіталей між парами валентних атомних орбіталей. Це проілюстровано на малюнку 6.1.2, де поляризація dp орбіталів на C і O, як видно, сприяє утворенню$p$ орбітальної зв'язку карбонільної групи, дозволяючи поляризувати$p_\pi$ орбіталі атома вуглецю вправо та$p_\pi$ орбіталі атома кисню вліво.

Малюнок 6.1.2 Кисень і вуглець утворюють$\pi$ зв'язок, який використовує поляризаційні функції на кожному атомі

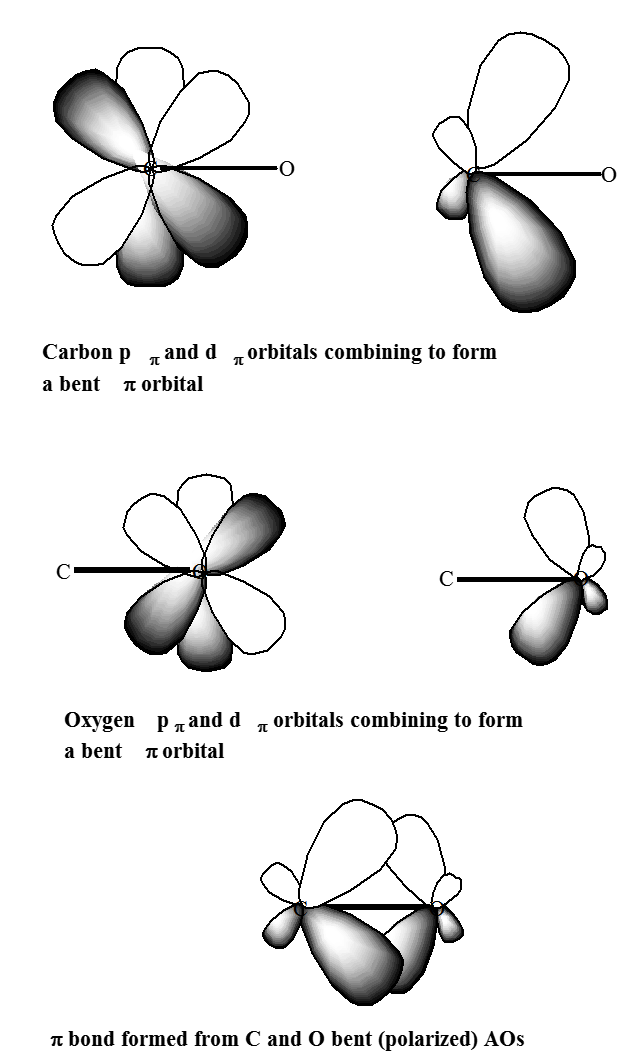
Функції поляризації мають важливе значення в напружених кільцевих сполуках, таких як циклопропан, оскільки вони забезпечують кутову гнучкість, необхідну для направлення електронної щільності в області між зв'язаними атомами, але вони також важливі в ненапружених сполуках, коли потрібна висока точність.

Дифузні функції

Маючи справу з аніонами або станами Рідберга, потрібно додатково збільшити базовий набір АТ шляхом додавання так званих дифузних базисних орбіталів. Описані вище функції валентності та поляризації не забезпечують достатньої радіальної гнучкості, щоб адекватно описати будь-який із цих випадків. База даних веб-сайту PNNL, наведена вище, пропонує гарне джерело для отримання дифузних функцій, відповідних різним атомам, як це робить сайт професора Кірка Петерсона.

Після визначення атомної орбітальної основи для кожного атома в молекулі, процедура LCAO-MO може бути використана для визначення$\chi_{\mu,i}$ коефіцієнтів, що описують зайняті та віртуальні (тобто незайняті) орбіталі. Важливо пам'ятати, що базові орбіталі самі по собі не є орбіталями SCF ізольованих атомів; навіть належні атомні орбіталі є комбінаціями (з атомними значеннями для$\chi_{\mu,i}$ коефіцієнтів) базисних функцій. Сам процес LCAO-MO-SCF визначає величини і ознаки$\chi_{\nu,i}$. Зокрема, саме чергування в знаках цих коефіцієнтів дозволяють утворюватися радіальні вузли.