3.2: Нормальні режими вібрації

Last updated
Save as PDF

Page ID: 19051

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Побачивши, як можна використовувати інформацію про градієнти та Гессіани на поверхні Борна-Оппенгеймера, щоб знайти геометрії, що відповідають стабільним видам та перехідним станам, давайте тепер перейдемо до того, як ці самі дані використовуються для обробки вібрацій на цій поверхні.

Для багатоатомної молекули, електронна енергія якої залежить від\(3N\) декартових координат її\(N\) атомів, потенційна енергія\(V\) може бути виражена (приблизно) через розширення ряду Тейлора щодо будь-якого з локальних мінімумів. Звичайно, різні локальні мінімуми (тобто різні ізомери) матимуть різні значення для координат рівноваги і для похідних енергії щодо цих координат. Розширення електронної енергії серії Тейлора пишеться як:

\[V (g_k) = V(0) + \sum_k \left(\dfrac{\partial V}{\partial q_k}\right) q_k + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \, + \, ... \]

Ось,

\(V(0)\)це енергія при поточній геометрії,
\(\dfrac{\partial{V}}{\partial{q_k}} = g_k\)- градієнт енергії по\(q_k\) координаті,
\(H_{j,k} = \dfrac{\partial^2{V}}{\partial{q_j}\partial{q_k}}\)є другою похідною або матрицею Гессіана, і
\(g_k\)довжина «кроку», яку потрібно зробити вздовж цього декартового напрямку.

Якщо геометрія відповідає мінімальному або перехідному стану, градієнтні члени зникнуть, а матриця Гессена матиме\(3N - 5\) (для лінійних видів) або\(3N -6\) (для нелінійних молекул) додатними власними значеннями і 5 або 6 нульовими власними значеннями (відповідними 3 поступальним і 2 або 3 обертальним) руху молекули) для мінімального та одного від'ємного власних значень\(3N-6\) і/або\(3N-7\) позитивних власних значень для перехідного стану.

Рівняння руху Ньютона для вібрації

Матриці кінетичної та потенційної енергії

Скорочуючи ряд Тейлора в квадратичних домінантах (якщо припустити, що ці терміни домінують, оскільки цікавлять лише невеликі зсуви від геометрії рівноваги), у людини є так званий гармонічний потенціал:

\[V(q_k) = V(0) + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \label{3.2.1} \]

Класичні механічні рівняння руху для\(3N \{q_k\}\) координат можна записати через вищевказану потенційну енергію та наступну функцію кінетичної енергії:

\[T = \dfrac{1}{2} \sum_j m_j \left(\dfrac{dq_j}{dt}\right)^2, \label{3.2.2}\]

де\(\dfrac{dq_j}{dt}\) - часова швидкість зміни координати\(q_j\) і\(m_j\) - маса атома, на якому знаходиться\(j^{th}\) декартова координата. Отримані таким чином рівняння Ньютона:

\[m_j\dfrac{d^2 q_j}{dt^2}=-\sum_k H_{j,k}q_k \]

де сила по\(j^{th}\) координаті задається мінус похідною потенціалу\(V\) по цій координаті

\[\dfrac{\partial{V}}{\partial{q_j}}= \sum_k H_{j,k} q_k \label{3.2.3}\]

в межах гармонійного наближення. Ці класичні рівняння можуть бути більш компактно виражені в терміні еволюції часу множини так званих масово зважених декартових координат, визначених як:

\[x_j = q_j \sqrt{(m_j)} \label{3.2.4}\]

з точки зору яких наведені вище рівняння Ньютона стають

\[\dfrac{d^2 x_j}{dt^2}=-\sum_k H'_{j,k}x_k\]

і зваженими по масі елементами матриці Гессіана є

\[ H'_{j,k} = \dfrac{H_{j,k}}{ \sqrt{m_jm_k} }. \label{3.2.5}\]

Гармонічні коливальні енергії та власні вектори нормального режиму

Припускаючи, що\(x_j\) проходять певну форму синусоїдальної еволюції часу:

\[x_j(t) = x_j (0) \cos(\omega t),\]

і підставляючи це в рівняння Ньютона, утворюється матричне рівняння власних значень:

\[\omega^2 x_j = \sum_k H'_{j,k} x_k \]

в якому власними значеннями є квадрати так званих коливальних частот нормального режиму, а власні вектори дають амплітуди руху по кожній з\(3N\) зважених по масі декартових координат, які належать кожній моді. Отже, для виконання нормального аналізу молекули формується зважений по масі матриця Гессена, а потім знаходить\(3N-5\) або\(3N-6\) ненульові власні значення, а\(\omega_j^2\) також відповідні власні вектори\(x_k^{(j)}\).

Корисно відзначити, що, якби цей самий вид аналізу виконувався при геометрії, що відповідає перехідному стану,\(3N-6\) або\(3N-7\)\(\omega_j^2\) значення були б позитивними, але одне з них було б негативним. Власний вектор, відповідний від'ємному власному значенню зважених по масі точок Гессена вздовж дуже важливого напрямку, про який ми поговоримо пізніше; це напрямок так званої координати внутрішньої реакції (IRC). При повідомленні про власні значення\(\omega_j^2\) при такій геометрії перехідного стану часто говорять, що існує одна уявна частота через те, що одне з\(\omega_j^2\) значень негативне; це значення\(\omega_j^2\) характеризує кривизну енергетичної поверхні по IRC при перехідному стані. Додатні коливальні власні значення геометрії перехідного стану використовуються, як розглянуто в розділі 8, для оцінки функцій розподілу статистичної механіки для швидкостей реакції, а негативне\(\omega_j^2\) значення відіграє певну роль у визначенні ступеня тунелювання через бар'єр на поверхні реакції.

В рамках цієї гармонійної обробки коливального руху сумарна коливальна енергія молекули задається як

\[E(\nu_1, \nu_2, ··· \nu_{3N-5\text{ or }6}) =\sum_{j=1}^{3N-5\text{ or }6}\hbar\omega_j\Big(\nu_j+\dfrac{1}{2}\Big) \]

сума\(3N-5\) або\(3N-6\) незалежні внески по одному для кожного нормального режиму. Відповідна загальна коливальна хвильова функція

\[\Psi = \prod_{j=1}^{3N-5\text{ or }6} \psi\nu_j (x^{(j)}) \]

є добутком\(3N-5\) або\(3N-6\) гармонічних функцій осцилятора по\(\psi\nu_j (x^{(j)})\) одному для кожного нормального режиму. Енергетичний проміжок між одним коливальним рівнем і іншим, в якому одне з\( \nu_j\) квантових чисел збільшено одиницею (тобто для фундаментальних коливальних переходів), становить

\[\Delta E_{\nu_j} \rightarrow \nu_j + 1 = \hbar \omega_j \]

Гармонічна модель таким чином передбачає, що переходи «фундаментальна» (\(\nu=0 \rightarrow \nu = 1\)) і «гаряча смуга» (\(\nu=1 \rightarrow \nu = 2\)) повинні відбуватися при одній енергії, а переходи обертона (\(\nu=0 \rightarrow \nu=2\)) повинні відбуватися рівно в два рази більше цієї енергії.

Можна задатися питанням, чи краще чи доцільніше використовувати декартові координати з масою при розміщенні мінімумів та перехідних станів на енергетичних поверхнях Борна-Оппенгеймера. Хоча масово зважені координати дійсно важливі для оцінки гармонічних коливальних частот і, як ми побачимо пізніше, для відстеження так званих внутрішніх реакційних шляхів, їх використання створює ті самі мінімуми та перехідні стани, які можна знайти, використовуючи координати, які є зваженими по масі. Це пов'язано з тим, що умова, що всі компоненти градієнта

\[\dfrac{\partial V}{\partial q_j}=0\]

енергетичної поверхні зникають на мінімумі або при перехідному стані автоматично підкоряються, коли виражаються через масово зважених координат, оскільки

\[\dfrac{\partial V}{\partial q_j}=\dfrac{\partial V}{\partial x_j}\dfrac{\partial x_j}{\partial q_j}=\dfrac{\partial V}{\partial x_j}\sqrt{m_j}\]

Зверніть увагу, що це означає, що геометрії всіх локальних мінімумів і перехідних станів на даній поверхні Борна-Оппенгеймера будуть точно однаковими незалежно від того, які ізотопи з'являються в молекулі. Наприклад, для реакцій

\[ H-CN \rightarrow H-NC \]

або

\[D-CN \rightarrow D-NC \]

\[ H_2C=O \rightarrow H_2 + CO\]

або

\[HDC=O \rightarrow HD + CO\]

або

\[D_2C=O \rightarrow D_2 + CO \]

геометрія реагентів, продуктів та перехідних станів (для кожної з різних реакцій) не залежатиме від ідентичності ізотопів водню. Однак гармонічні коливальні частоти залежатимуть від ізотопів, оскільки зважений по масі Гессіан відрізняється від Гессіана, вираженого через невагові координати.

Використання симетрії

Адаптовані режими симетрії

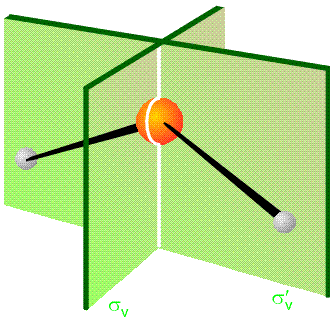
Часто можна спростити розрахунок нормальних режимів гармонічних частот і власних векторів шляхом використання молекулярної точкової групової симетрії. Для молекул, що володіють симетрією при певній стійкій геометрії, електронний потенціал\(V(q_j)\) відображає симетрію щодо переміщень еквівалентних декартових координат симетрії. Наприклад, розглянемо молекулу води в її\(C_{2v}\) рівноважної геометрії, як показано на малюнку 3.2. Дуже малий рух лівого\(H\) атома\(H_2O\) молекули в позитивному\(x\) напрямку (\(\Delta x_L\)) виробляє таку ж зміну потенціалу,\(V\) як відповідно невелике зміщення правого\(H\) атома в негативному\(x\) напрямку

(\(-\Delta x_R\)). Аналогічно, рух лівої H в позитивному напрямку y (\(\Delta y_L\)) виробляє зміну енергії, ідентичну руху правого H в позитивному напрямку y (\(\Delta y_R\)).

Малюнок 3.2. Молекула води, що показує дві довжини зв'язку та кут

Еквівалентність пар декартових координатних зміщень є результатом того, що вектори зміщення пов'язані точковими груповими операціями\(C_{2v}\) групи. Зокрема, відбиття\(\Delta x_L\) через площину yz (дві площини зображені на малюнку 3.3) виробляє\(-\Delta x_R\), а відображення\(\Delta y_L\) через цю саму площину дає\(\Delta y_R\).

Малюнок 3.3. Дві площини симетрії молекули води.

Більш загально, можна об'єднати множини декартових координат зміщення {\(q_k\)} в так звані адаптовані до симетрії координати {\(Q_{\Gamma_j}\)}, де індекс\(\Gamma\) позначає нескорочуване подання у відповідній групі точок, а j позначає певну комбінацію цієї симетрії ( тобто може бути більше одного виду зсуву, що має задану симетрію (G). Ці адаптовані до симетрії координати можуть бути сформовані шляхом застосування операторів проекції точок групи (які детально розглядаються в розділі 4) до окремих декартових координат переміщення.

Для ілюстрації знову розглянемо\(H_2O\) молекулу в описаній вище системі координат. \(3N = 9\)Масово-зважені декартові координати зміщення (\(X_L, Y_L, Z_L, X_O, Y_O, Z_O, X_R, Y_R, Z_R\)) можуть бути адаптовані симетрією, застосовуючи наступні чотири оператори проекції:

\[P_{A_1} = 1 + \sigma_{yz} + \sigma_{xy} + C_2 \]

\[P_{b_1} = 1 + \sigma_{yz} - \sigma_{xy} - C_2 \]

\[P_{b_2} = 1 - \sigma_{yz} + \sigma_{xy} - C_2 \]

\[P_{a_2} = 1 - \sigma_{yz} - \sigma_{xy} + C_2 \]

до кожної з 9 вихідних координат (символ s позначає відображення через площину і\(C_2\) означає обертання навколо\(C_2\) осі молекули). Звичайно, не вийде 9 х 4 = 36 незалежних симетрії адаптованих координат таким чином; виникне багато однакових комбінацій, і тільки 9 будуть незалежними.

Незалежні комбінації\(a_1\) симетрії (нормовані для отримання векторів одиничної довжини)

\[Q_{a_1,1} = \dfrac{1}{\sqrt{2}} [X_L- X_R]\]

\[Q_{a_1,2} = \dfrac{1}{\sqrt{2}} [Y_L + Y_R]\]

\[Q_{a_1,3} = [Y_O]\]

Ті, що мають\(b_2\) симетрію

\[Q_{b_2,1} = \dfrac{1}{\sqrt{2}} [X_L+ X_R]\]

\[Q_{b_2,2} = \dfrac{1}{\sqrt{2}} [Y_L - Y_R]\]

\[Q_{b_2,3} = [X_O],\]

і комбінації

\[Q_{b_1,1} = \dfrac{1}{\sqrt{2}} [Z_L + Z_R]\]

\[Q_{b_1,2} = [Z_O]\]

мають\(b_1\) симетрію, тоді як

\[Q_{a_2,1} = \dfrac{1}{\sqrt{2}} [Z_L - Z_R]\]

має\(a_2\) симетрію.

Точкова групова симетрія гармонічного потенціалу

Ці дев'ять адаптованих до симетрії координат\(Q_{\Gamma_j}\) виражаються як унітарні перетворення вихідних масово зважених декартових координат:

\[Q_{\Gamma_j} = C_{\Gamma_{j,k}} X_k \]

Ці коефіцієнти перетворення\({C_{\Gamma_{j,k}}}\) можуть бути використані для здійснення унітарного перетворення матриці Гессена 9х9. При цьому нам знадобляться тільки форми блоків

\[H_{\Gamma_{j,l}} = \sum_{k,k’} C_{\Gamma_{j,k}} H_{k,k'} \sqrt{m_k m_{k'}} C_{\Gamma_{l,k'}} \]

всередині якого симетрії двох режимів ідентичні. Позадіагональні елементи

\[H_{\Gamma_j\Gamma'_l}= \sum_{k,k’} C_{\Gamma_{j,k}} H_{k,k'} \sqrt{m_k m_{k'}} C_{\Gamma'_{l,k'}} \]

зникають, оскільки потенціал\(V(q_j)\) (і повний вібраційний гамільтоніан\(H = T + V\)) комутується з операціями симетрії\(C_{2V}\) точкової групи.

Як результат, зважений по масі 9х9 задачу на власні значення Гессена можна розділити на дві матричні задачі 3х3 (про\(a_1\) та\(b_2\) симетрію), одну матрицю\(b_1\) симетрії 2х2 та одну матрицю\(a_2\) симетрії 1х1. Наприклад, блок\(a_1\) симетрії Гиса формується наступним чином:

\ [
\ лівий [\ почати {масив} {ccc}
\ dfrac {1} {\ sqrt {2}} & -\ dfrac {1} {\ sqrt {2}} & 0
\\ dfrac {1}} &\ dfrac {1} {\ sqrt {2}} & 0\
0 & 1\ кінець {масив}
\ праворуч]\ ліворуч [
\ begin {масив} {ccc}
m_h^ {-1/2}\ dfrac {\ частковий ^ 2 V} {\ частковий x_L^2} м_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ частковий x_L\ частковий x_r} м_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ частковий x_2}} {\ часткова x_L\ часткова Y_O} м_h^ {-1/2}\
m_h^ {-1/2}\ dfrac {\ часткова ^2 V} {\ часткова x_r\ часткова x_L} м_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ частковий ^ 2 V} {\ частковий x_r^2} м_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ частковий x_r\ частковий Y_O} м_h^ {-1/2}\ m_h^ {-1/2}\
dfrac {\ частковий ^ 2 V} {\ частковий Y_O\ частковий x_L} м_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ частковий ^ 2 V} {\ частковий Y_O\ частковий x_r} м_h^ {-1/2} & m_h^ {-1/2}\ dfrac {\ частковий ^ 2 V} {\ частковий Y_O^2} m_h^ {-1/2}
\ кінець {масив}\ праворуч]
\ лівий [\ почати {масив} {ccc}
\ dfrac {1} {\ sqrt {2}} &\ dfrac {1} {\ sqrt {2}} & 0\\
-\ dfrac {1} {\ sqrt {2} {\ sqrt {2}} & 0\
0 & 0 & 1
\ кінець {масив}\ праворуч]
\]

The\(b_2\),\(b_1\) і\(a_2\) блоки формуються аналогічним чином. Власні значення кожного з цих блоків забезпечують квадрати гармонічних коливальних частот, власні вектори забезпечують коефіцієнти\(\{C_{\Gamma_{j,k}}\}\)\(j^{\rm th}\) нормального режиму симетрії через\(\Gamma\) масово зважених декартових координат {\(X_k\)}. Потім співвідношення\(X_k = q_k \sqrt{(m_k)}\) може бути використано для вираження цих коефіцієнтів через початкові декартові координати {\(q_k\)}.

Незалежно від того, чи використовується симетрія для блокування діагоналізації масово зважених Гессіана, шість (для нелінійних молекул) або п'ять (для лінійних видів) власних значень дорівнюватиме нулю. Власні вектори, що належать цим нульовим власним значенням, описують 3 переклади і 2 або 3 обертання молекули. Наприклад, при вираженні в терміні початкових (тобто немасово зважених) декартових координат

\[\dfrac{1}{\sqrt{3}}[x_L + x_R + x_O]\]

\[\dfrac{1}{\sqrt{3}}[y_L + y_R + y_O]\]

\[\dfrac{1}{\sqrt{3}}[z_L +z_R + z_O]\]

є трьома перекладами власних векторів\(b_2\),\(a_1\) і\(b_1\) симетрії, і

\[\dfrac{1}{\sqrt{2}}(z_L-z_R)\]

є обертанням (навколо осі у на малюнку 3.2)\(a_2\) симетрії. Цей вектор обертання може бути сформований шляхом застосування оператора\(a_2\) проекції до\(z_L\) або до\(z_R\). Інші два обертання мають\(b_2\) симетрію\(b_1\) і передбачають обертання молекули навколо\(x\) - і\(z\) - осей малюнка 3.2 відповідно.

Отже, з 9 декартових переміщень 3 мають\(a_1\) симетрію, 3 з\(b_2\), 2 з\(b_1\) і 1 з\(a_2\). З них є три переклади (\(a_1\)\(b_2\), і\(b_1\)) і три обертання (\(b_2\)\(b_1\), і a2). Це залишає дві вібрації\(a_1\) і одну\(b_2\) симетрії. Для розглянутого тут\(H_2O\) прикладу три ненульові власні значення масово зважених Гессіана є, отже\(a_1\)\(b_2\), і\(a_1\) симетрія. Вони описують симетричні і асиметричні коливання розтягування і режим вигину відповідно, як показано на малюнку 3.4.

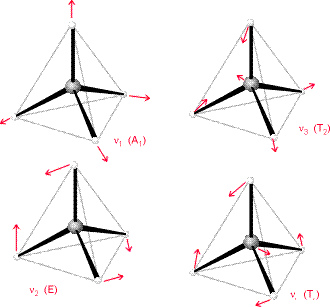
Малюнок 3.4: Симетричні та асиметричні режими розтягування та режим згинання води

Представлений тут метод коливального аналізу може працювати для будь-якої багатоатомної молекули. Один знає зважений по масі Гессіан, а потім обчислює ненульові власні значення, які потім забезпечують квадрати гармонічних коливальних частот нормальних режимів. Точкова групова симетрія може бути використана для блокування діагоналізації цього Гессіана та для позначення коливальних режимів відповідно до симетрії, як ми показуємо на малюнку 3.5 для\(CF_4\) молекули в тетраедральній симетрії.