3.1: Стратегії оптимізації геометрії та пошуку перехідних станів

Last updated
Save as PDF

Page ID: 19050

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Розширення гармонічних і коливальних моделей Морзе на багатоатомні молекули вимагає, щоб багатовимірна енергетична поверхня була проаналізована таким чином, що дозволяє наблизити руху молекули з точки зору багатьох майже незалежних коливань. У цьому розділі ми розглянемо інструменти, які використовуються для проведення такого аналізу поверхні, але спочатку важливо описати, як на таких поверхнях можна знайти геометрію мінімальної енергії та перехідного стану.

Пошук місцевих мінімумів

Багато стратегій, які намагаються знайти мінімуми на молекулярно-потенційних енергетичних ландшафтах, починаються з наближення потенційної енергії\(V\) для геометрії (спільно позначається через\(3N\) декартові координати\(\{q_j\}\)) в розширенні серії Тейлора про деяку «вихідну точку» геометрії (тобто, поточна молекулярна геометрія в ітераційному процесі або геометрія, яку ви вгадали як розумну для мінімального або перехідного стану, який ви шукаєте):

\[V (g_k) = V(0) + \sum_k \left(\dfrac{\partial V}{\partial q_k}\right) q_k + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} q_k \, + \, ... \label{3.1.1}\]

Ось,

\(V(0)\)це енергія при поточній геометрії,
\(\dfrac{\partial{V}}{\partial{q_k}} = g_k\)- градієнт енергії по\(q_k\) координаті,
\(H_{j,k} = \dfrac{\partial^2{V}}{\partial{q_j}\partial{q_k}}\)є другою похідною або матрицею Гессіана, і
\(g_k\)довжина «кроку», яку потрібно зробити вздовж цього декартового напрямку.

Приклад енергетичної поверхні лише в двох вимірах наведено на малюнку 3.1, де проілюстровані різні особливі аспекти. Наприклад, відображаються мінімуми, що відповідають стабільним молекулярним структурам, перехідні стани (точки сідла першого порядку), що з'єднують такі мінімуми, і точки сідла вищого порядку.

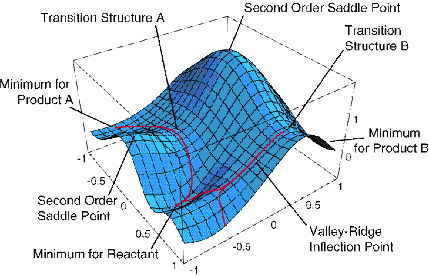
Малюнок 3.1. Двовимірна потенційна поверхня, що показує мінімуми, перехідні стани та шляхи, що з'єднують їх.

Якщо єдиним знанням, яке є, є\(V(0)\) і градієнтні компоненти (наприклад, обчислення других похідних, як правило, набагато більш обчислювальним оподаткуванням, ніж оцінка градієнта, тому часто змушують працювати, не знаючи елементів матриці Гессіана), лінійне наближення

\[V(q_k) = V(0) + \sum_k g_K \,q_k \label{3.1.2}\]

припускає, що слід вибирати елементи «крок»\(q_k\), протилежні за знаком від відповідних елементів градієнта,\(g_k = \dfrac{\partial{V}}{\partial{q_k}}\) якщо хочеться рухатися «вниз» до мінімуму. Величина елементів кроку зазвичай тримається невеликою, щоб залишатися в межах «радіуса довіри», в межах якого лінійне наближення дійсне до певної заздалегідь визначеної бажаної точності (тобто хочеться запевнити, що\(\sum_k g_K q_k\) це не надто велика).\(V\)

Коли доступні другі похідні дані, існують різні підходи до прогнозування того, який крок {\(g_k\)} зробити в пошуках мінімуму, і саме в рамках таких стратегій, заснованих на Гессіані, виникає концепція кроку по\(3N-6\) незалежних режимах. Спочатку пишемо квадратичне розширення Тейлора

\[V (g_k) = V(0) + \sum_k g_K g_k + \dfrac{1}{2} \sum_{j,k} q_j H_{j,k} g_k\label{3.1.3}\]

в матрично-векторних позначеннях

\[V(\textbf{q}) = V(0) + \textbf{q}^{\textbf{T}} \cdot \textbf{g} + \dfrac{1}{2} \textbf{q}^{\textbf{T}} \cdot \textbf{H} \cdot \textbf{q} \label{3.1.4}\]

з елементами,\(\{g_k\}\) зібраними в вектор стовпця\(\textbf{q}\), транспонування яких позначається\(\textbf{q}^{\textbf{T}}\).

Вводячи унітарну матрицю\(\textbf{U}\), яка діагоналізує симетричну\(\textbf{H}\) матрицю, вищевказане рівняння стає

\[V(\textbf{q}) = V(0) + \textbf{q}^{\textbf{T}} \textbf{U} \, \textbf{U}^{\textbf{T}} \textbf{q} + \dfrac{1}{2} \textbf{q}^{\textbf{T}} \textbf{U} \, \textbf{U}^{\textbf{T}} \textbf{H} \textbf{U}\, \textbf{U}^{\textbf{T}} \textbf{q}. \label{3.1.5}\]

Тому\(\textbf{U}^{\textbf{T}}\textbf{H}\textbf{U}\) що діагональ, у нас є

\[(\textbf{U}^{\textbf{T}}\textbf{H}\textbf{U})_{k,l} = \delta_{k,l} \lambda_k \label{3.1.6}\]

де\(\lambda_k\) - власні значення матриці Гессіана. Для нелінійних молекул ці власні значення будуть ненульовими; для лінійних молекул - ненульовими.\(3N-6\)\(3N-5\) 5 або 6 нульових власних значень\(\textbf{H}\) мають власні вектори, які описують трансляцію і обертання всієї молекули; вони дорівнюють нулю, оскільки енергетична поверхня\(V\) не змінюється, якщо молекула обертається або перекладається. Це може бути важко правильно ідентифікувати 5 або 6 перекладу і обертання власних значень Гессіана, оскільки проблеми з числовою точністю часто призводять до того, що вони виникають як дуже малі позитивні або негативні власні значення. Якщо досліджувана молекула насправді має внутрішні (тобто вібраційні) власні значення, які дуже малі (наприклад, крутильний рух метильної групи в етані має дуже малий енергетичний бар'єр, внаслідок чого енергія дуже слабо залежить від цієї координати), потрібно бути обережним, щоб правильно ідентифікувати переклад-обертання і внутрішні власні значення. Вивчаючи власні вектори, що відповідають всім низьким власним значенням Гессіана, можна ідентифікувати і таким чином відокремити перші від останніх. В решті цієї дискусії я припускаю, що обертання та переклади були належним чином визначені, і стратегії, які я обговорюю, стосуватимуться використання решти\(3N-5\) або\(3N-6\) власних значень та власних векторів для виконання серії «кроків» геометрії, призначених для визначення енергетичних мінімумів. і перехідних станів.

Власні вектори\(\textbf{H}\) формують стовпці масиву\(U\), що призводить\(H\) до діагональної форми:

\[\sum_{\lambda} H_{k,l} U_{l,m} = \lambda_m U_{k,m} \label{3.1.7}\]

Тому, якщо ми визначимо

\[Q_m = \sum_k U^T_{m,k} g_k \label{3.1.8a}\]

\[G_m = \sum_k U^T_{m,k} g_K \label{3.1.8b}\]

щоб бути складовою кроку\(\{g_k\}\) і градієнта вздовж власного\(m^{th}\) вектора\(H\), квадратичне розширення\(V\) може бути записано через кроки вздовж\(3N-5\) або\(3N-6 \{Q_m\}\) напрямків, які відповідають ненульовим власним значенням Гессіана:

\[V (g_k) = V(0) + \sum_m G^T_m Q_m + \dfrac{1}{2} \sum_m Q_m \lambda_m Q_m.\label{3.1.9}\]

Перевага перетворення градієнта, кроку та Гессіана на основу власного режиму полягає в тому, що кожен такий режим (позначений m) з'являється в незалежній незв'язаній формі в розширенні\(V\). Це дозволяє робити кроки по кожному з\(Q_m\) напрямків незалежним чином з кожним кроком, покликаним знизити потенційну енергію, коли ми шукаємо мінімуми (стратегії знаходження перехідного стану будуть розглянуті нижче).

Для кожного напрямку власного режиму можна запитати, який крок\(Q\) розміру\(GQ + \dfrac{1}{2} \lambda Q^2\) буде мінімальним. Диференціація цієї квадратичної форми по відношенню до\(Q\) і встановлення результату рівного нулю дає

\[Q_m = - \dfrac{G_m}{\lambda_m} \label{3.1.10}\]

тобто слід зробити крок навпроти градієнта, але з величиною, заданою градієнтом, розділеним на власне значення матриці Гессіана. Якщо поточна молекулярна геометрія є такою, яка має всі позитивні\(\lambda_m\) значення, це вказує на те, що на енергетичній поверхні може бути «близько» до мінімуму (тому що всі\(\lambda_m\) позитивні на мінімумах). У такому випадку крок\(Q_m = - G_m/\lambda_m\) протиставляється градієнту вздовж усіх\(3N-5\) або\(3N-6\) напрямків, подібно до стратегії на основі градієнтів, розглянутої раніше запропонованої. Зміна енергії, яка, як очікується, відбудеться, якщо крок буде\(\{Q_m\}\) зроблений, можна обчислити шляхом підстановки\(Q_m = - G_m/\lambda_m\) в квадратне рівняння для\(V\):

\[V(\text{after step}) = V(0) + \sum_m G^T_m \bigg(- \dfrac{G_m}{\lambda_m}\bigg) + \dfrac{1}{2} \sum_m \lambda_m \bigg(- \dfrac{G_m}{\lambda_m}\bigg)^2 \label{3.1.11a}\]

\[= V(0) - \dfrac{1}{2} \sum_m \lambda_m \bigg(- \dfrac{G_m}{\lambda_m}\bigg)^2. \label{3.1.11b}\]

Це чітко говорить про те, що крок призведе до «спуску» в енергії вздовж кожного власного режиму до тих пір, поки всі\(\lambda_m\) значення будуть позитивними. Наприклад, якби почати з хорошої оцінки рівноважної геометрії етилену та пропену, можна було б розмістити ці дві молекули на відстані,\(R_0\) більшій, ніж очікувана міжфрагментна рівноважна відстань\(R_{\rm vdW}\) у комплексі ван дер Ваальса, що утворюється при їх взаємодії. Оскільки обидва фрагменти знаходяться поблизу власної геометрії рівноваги і на\(R_0\) відстані, на якій сили привабливості на великі відстані будуть діяти, щоб зібрати їх разом, стратегія, така як викладена вище, може бути використана для визначення мінімуму ван дер Ваальса на їх енергетичній поверхні. Цей мінімум зображений якісно на малюнку 3.1а.

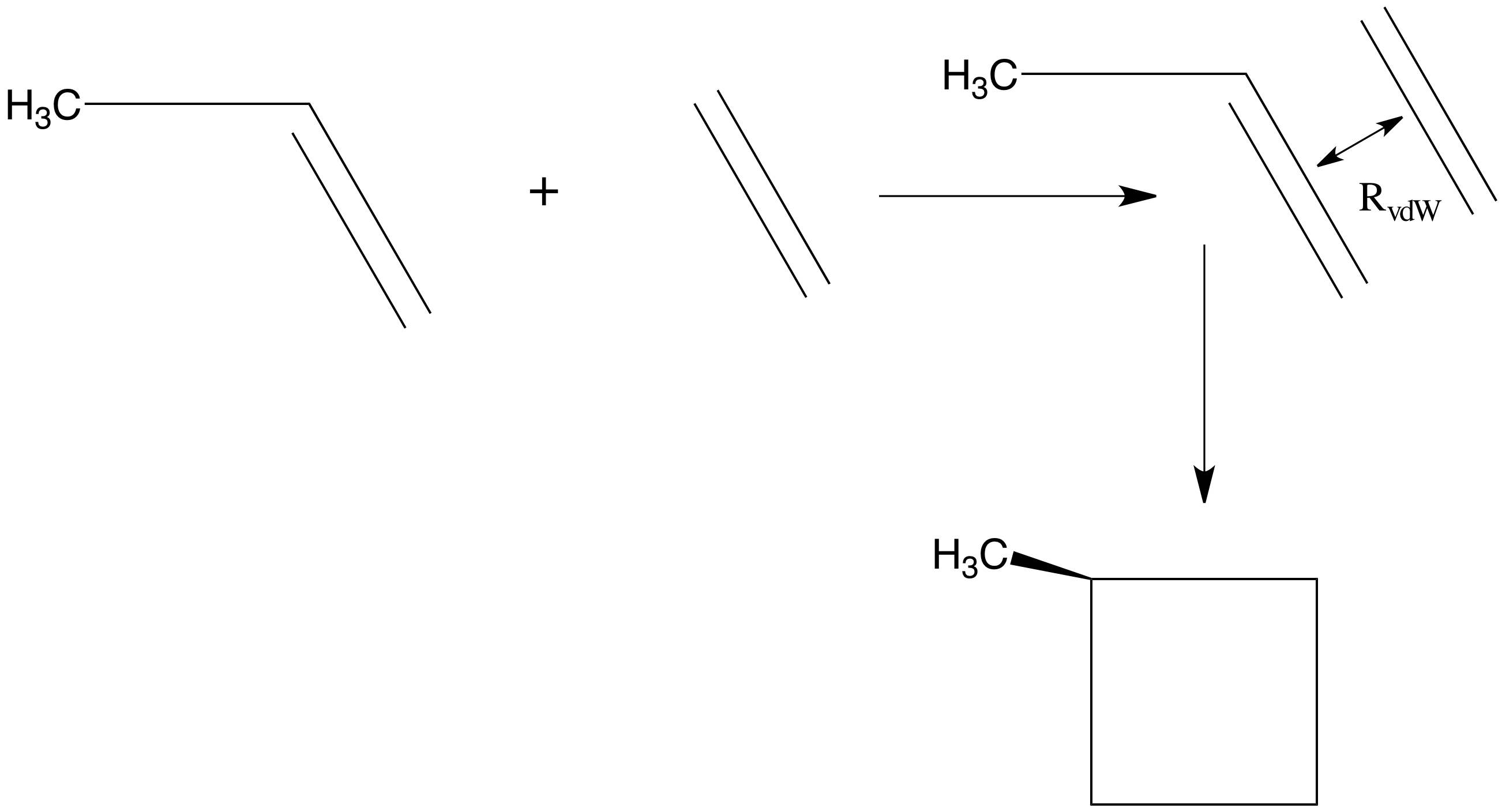
Малюнок 3.1a Комплекс Ван дер Ваальса (вгорі праворуч) утворюється між етиленом і пропеном, геометрія якого може бути розташована за рецептом, описаним вище. Продукт реакції [2+2] цикло-приєднання, метил-циклобутан (нижній правий).

Починаючи з того\(R_0\), можна виявити, що\(3N-6 = 39\) з власнихзначень матриці Гессена ненульові, де\(N = 15\) - загальна кількість атомів в комплексі етилен - пропена. З цих 39 ненульових власних значень три матимуть власні вектори, що описують радіальні та кутові зміщення двох фрагментів відносно один одного; решта 36 опишуть внутрішні коливання комплексу. Власні значення, що належать до міжфрагментних радіальних і кутових переміщень, можуть бути позитивними або негативними (оскільки ви не робили жодної особливої спроби орієнтувати молекули під оптимальними кутами, і ви, можливо, не дуже добре здогадалися на оптимальній рівноважній міжфрагментовій відстані), тому, ймовірно, було б розумніше почати процес енергомінімізації, використовуючи градієнтну інформацію для кроку вниз в енергії, поки не досягне геометрії,\(R_1\) при якій всі 39 власних значень матриці Гессіана є позитивними. З цього моменту кроки, визначені як градієнтом, так і Гессіаном (тобто\(Q_m = - G_m/\lambda_m\)), можуть бути використані, якщо не зустрітися з геометрією, у якій одне з власних значень\(\lambda_m\) дуже мало, і в цьому випадку крок\(Q_m = - G_m/\lambda_m\) вздовж цього власного режиму може бути нереально великим. У цьому випадку краще не взяти\(Q_m = - G_m/\lambda_m\) за крок уздовж цього конкретного напрямку, а зробити невеликий крок у напрямку, протилежному ухилу, щоб підвищити шанси на рух вниз. Такі проблеми з малими власними значеннями можуть виникнути, наприклад, якщо кут кручення метильної групи пропена під час послідовності кроків геометрії переміщатися в область, де доступні затемнені, а не шахові геометрії. Близько затемнених геометрій власне значення Гессіана, що описує скручування метильної групи, є негативним; поблизу шахових геометрій воно позитивне.

Всякий раз, коли один або кілька з них\(\lambda_m\) є негативними в поточній геометрії, один знаходиться в області енергетичної поверхні, яка недостатньо близька до мінімуму, щоб сліпо слідувати рецепту\(Q_m = - G_m/\lambda_m\) вздовж усіх режимів. Якщо тільки один негативний, то передбачається, що він\(\lambda_m\) знаходиться поблизу перехідного стану (при якому всі компоненти градієнта зникають, а всі, крім одного,\(\lambda_m\) є позитивними з одним\(\lambda_m\) негативом). У такому випадку вищевказаний аналіз пропонує зробити крок\(Q_m = - G_m/\lambda_m\) уздовж усіх режимів, що мають позитивний\(\lambda_m\), але роблячи крок протилежного напрямку (наприклад,\(Q_n = - G_n/\lambda_n\) якщо не\(\lambda_m\) дуже малий, у цьому випадку найкращий невеликий крок\(G_n\) протилежний) вздовж напрямку, що має негативний \(\lambda_n\)якщо хтось намагається рухатися до мінімуму. Це те, що я рекомендував у попередньому пункті, коли зустрічається затемнена геометрія (яка є перехідним станом для обертання метильної групи), якщо хтось шукає енергетичного мінімуму.

Пошук перехідних держав

З іншого боку, якщо один знаходиться в області, де одне власне значення Гессіана є від'ємним (а решта - позитивними), а якщо хтось прагне знайти стан переходу, то робити кроки\(Q_m = - G_m/\lambda_m\) вздовж усіх режимів Маючи позитивні власні значення та приймаючи\(Q_n = - G_n/\lambda_n\) за собою режим, що має негативне власне значення, є відповідний. Кроки\(Q_m = - G_m/\lambda_m\) будуть діяти, щоб зберегти енергію поблизу її мінімуму уздовж усього, крім одного напрямку, і крок\(Q_n = - G_n/\lambda_n\) буде рухатися систему вгору в енергії вздовж напрямку, що має негативну кривизну, точно так, як хочеться, коли «йшов» в гору в потоці до гірського перевалу.

Однак навіть процедура, щойно викладена для знаходження перехідного стану, може призвести до оманливих результатів, якщо не використовується певна міра хімічної інтуїції. Дозвольте мені навести приклад, щоб проілюструвати цей момент. Припустимо, що потрібно знайти початок поблизу геометрії комплексу ван дер Ваальса за участю етилену та пропену, а потім знайти перехідний стан на шляху реакції, що веде до [2+2] продуктів цикло-додавання метил-циклобутану, як також показано на малюнку 3.1a. Розглянемо використання будь-якої з двох стратегій, щоб почати «прогулянку», що веде від комплексу ван дер Ваальса до бажаного стану переходу (TS):

Можна знайти найнижче (без перекладу або без обертання) власне значення Гессіана і зробити невеликий крок в гору уздовж цього напрямку, щоб розпочати потокову прогулянку, яка може призвести до TS. Використання найменшого власного значення Гессіана для визначення напрямку для дослідження має сенс, оскільки саме уздовж цього напрямку енергетична поверхня піднімається найменш різко (принаймні поблизу геометрії реагентів).
Можна трохи перемістити етилен радіально (скажімо 0.2 Å) ближче до пропену, щоб створити початкову геометрію, щоб почати пошук TS. Це має сенс, оскільки відомо, що реакція повинна призвести до міжфрагментних вуглецево-вуглецевих відстаней, які набагато коротші в метил-циклобутанових продуктах, ніж у комплексі ван дер Ваальса.

Перша стратегія, запропонована вище, швидше за все, зазнає невдачі, оскільки серія кроків, породжених ходьбою в гору вздовж найнижчого власного режиму Гессена, створить шлях, що веде від затемненої до шахової орієнтації метильної групи пропену. Дійсно, цей шлях веде до TS, але ми хочемо не [2+2] цикло-додавання TS. Урок на дому полягає в тому, що прогулянки по потоку в гору, що починаються як мінімум на потенційній енергетичній поверхні реагентів, можуть або не можуть призвести до бажаного TS. Такі прогулянки не є нерозумними, але слід вивчити природу власного режиму, що дотримується, щоб судити, чи мають зміщення вздовж цього режиму хімічний сенс. Зрозуміло, що лише обертання метильної групи не є хорошим способом переходу від етилену та пропену до метил-циклобутану.

Друга стратегія, запропонована вище, може бути успішною, але її, ймовірно, все ще потрібно буде доопрацювати. Наприклад, якби зміщення етилену до пропену було занадто малим, не можна було б спотворювати систему достатньо, щоб перемістити її в область, де енергетична поверхня має негативну кривизну вздовж шляху реакції, як вона повинна мати при наближенні до TS. Отже, якщо власні моди Гессіана, власні вектори яких мають суттєві міжфрагментні радіальні зсуви, є позитивними, то, ймовірно, один не змістив два фрагменти досить близько один до одного. Ймовірно, найкращим способом цього продовжити було б перемістити два фрагменти ще ближче (або, щоб перемістити їх уздовж лінійного синхронного шляху [1], що з'єднує реагенти та продукти), поки не знайдеться геометрія, при якій власний режим негативного власного значення Гессіана має суттєві компоненти вздовж того, що, здається, розумним для бажаного шляху реакції (тобто значних переміщень, що призводять до коротших міжфрагментних вуглецево-вуглецевих відстаней). Після того, як ви знайшли таку геометрію, можна використовувати стратегії, деталізовані раніше (наприклад,\(Q_m = - G_m/\lambda_m\) щоб потім йти в гору уздовж одного режиму, мінімізуючи при цьому уздовж інших режимів, щоб рухатися до TS. У разі успіху такий процес призведе до ТЗ, при якому всі складові градієнта зникнуть і всі, крім одного, власне значення Гессіана, є позитивним. Взяти домашній урок прикладу полягає в тому, що розумно спробувати спочатку знайти геометрію, досить близьку до TS, щоб викликати у Гессіана негативне власне значення, власний вектор якого має істотний характер уздовж напрямків, які мають хімічний сенс для шляху реакції.

У ряді кроків до мінімуму або до TS, як тільки крок був запропонований в межах основи власного режиму, потрібно висловити цей крок з точки зору оригінальних декартових координат, щоб ці декартові значення\(q_k\) могли бути змінені в програмній програмі для здійснення передбачуваного кроку. Задані значення для\(3N-5\) або\(3N-6\) крокових компонентів\(Q_m\) (наприклад, крокові компоненти\(Q_m\) вздовж 5 або 6 режимів, що мають нульові власні значення Гессіана, можуть бути прийняті нульовими, оскільки вони просто переводять або обертають молекулу), потрібно обчислити {\(g_k\)}. Для цього ми використовуємо відносини

\[Q_m = \sum_k U^T_{m,k} g_k\label{3.1.12}\]

і запишіть її зворотну (використовуючи унітарний характер\(\textbf{U}\) матриці):

\[g_k = \sum_m U_{k,m} Q_m \label{3.1.13}\]

для обчислення потрібних декартових компонентів кроку.

Використовуючи описані вище підходи на основі Гессіана, потрібно проявляти особливу обережність, коли одне або кілька власних значень Гессіана малі. Таке часто трапляється, коли

одна має молекулу, що містить «м'які режими» (тобто ступені свободи, за якими енергія змінюється мало), або
при переміщенні з області негативної кривизни в область позитивної кривизни (або навпаки) - в таких випадках кривизна повинна рухатися через нуль або поблизу нього.

Для цих ситуацій вираз\(Q_m = - G_m/\lambda_m\) може виробляти дуже великий крок уздовж режиму, що має невелику кривизну. Необхідно дотримуватися обережності, щоб не допустити таких неправильних штучно великих кроків.

Енергетичні поверхневі перетину

Слід зазначити, що є й інші важливі області потенційних енергетичних поверхонь, які треба вміти знаходити та характеризувати. Вище ми зосередилися на локальних мінімумах і перехідних станах. Пізніше в цій главі, і знову в розділі 8, ми обговоримо, як слідувати так званим реакційним шляхом, які з'єднують ці два види стаціонарних точок, використовуючи тип градієнта та інформацію про Гессіан, яку ми ввели раніше в цій главі.

Іноді важливо знайти геометрії, при яких дві енергетичні поверхні Борна-Оппенгеймера\(V_1(\text{q})\) і\(V_2(\text{q})\) перетинаються, оскільки такі області часто служать ефективними воронками для траєкторій або хвильових пакетів, що розвиваються на одній поверхні, щоб пройти так звані неадіабатичні переходи на іншу поверхню. Давайте витратимо кілька хвилин на роздуми про те, за яких обставин такі поверхні дійсно можуть перетинатися, адже студенти часто чують, що поверхні не перетинаються, а натомість проходять уникнені перетину. Щоб зрозуміти проблему, припустимо, що у нас є дві хвильові функції,\(\Phi_1\) і\(\Phi_2\) обидві з яких залежать від\(3N-6\) координат\(\{q\}\). Ці дві функції не вважаються точними власними функціями гамільтоніана\(H\), але, ймовірно, обрані для наближення таких власних функцій. Щоб знайти вдосконалені функції\(\Psi_2\), які більш точно представляють власні\(\Psi_1\) стани, зазвичай формують лінійні комбінації\(\Phi_1\) і\(\Phi_2\),

\[ \Psi_K = C_{K,1} \Phi_1 + C_{K,2} \Phi_2 \label{3.1.14}\]

з якого виникає проблема з власним значенням матриці 2x2:

\ [\ left|\ почати {масив} {cc}
H_ {1,1} -E & H_ {1,2}\\
H_ {2,1} & H_ {2,1} & H_ {2,2} -E
\ end {масив}\ право|=0\]

Це квадратне рівняння має два розв'язки.

\[ 2E_\mp = (H_{1,1} + H_{2,2}) \pm \sqrt{(H_{1,1}+H_{2,2})^2 + 4H_{1,2}^2}\]

Ці два рішення можуть бути рівними (тобто дві енергії стану можуть перетинатися) тільки в тому випадку, якщо квадратний кореневий фактор зникне. Оскільки цей коефіцієнт є сумою двох квадратів (кожен з яких є додатними величинами), це може статися лише в тому випадку, якщо дві ідентичності тримаються одночасно (тобто в одній геометрії):

\[H_{1,1} = H_{2,2} \label{3.1.15a}\]

\[H_{1,2} = 0. \label{3.1.15b}\]

Основним моментом є те, що в\(3N-6\) розмірному просторі два стани, як правило, не матимуть рівної енергії. Однак у просторі двох нижчих вимірів (тому що є дві умови, які повинні одночасно підкорятися:\(H_{1,1} = H_{2,2}\) і\(H_{1,2} = 0\)), їх енергії можуть бути рівними. Вони не повинні бути рівними, але не виключено, що вони є. Він заснований на такому аналізі, що зазвичай говорять, що потенційні енергетичні поверхні в\(3N-6\) розмірах можуть зазнавати перетину в просторах розмірності\(3N-8\). Якщо два стани мають різну симетрію (наприклад, один - синглет, а інший - триплет), позадіагональний елемент\(H_{1,2}\) зникає автоматично, тому для реалізації перетину потрібна лише одна умова. Отже, ми говоримо, що два стани різної симетрії можуть перетинатися в просторі виміру\(3N-7\). Для триатомної молекули з\(3N-6 = 3\) внутрішніми ступенями свободи це означає, що поверхні однієї симетрії можуть перетинатися в просторі розмірності 1 (тобто вздовж лінії), тоді як поверхні різної симетрії можуть перетинатися в просторі виміру 2 (тобто в площині). Приклад такого перетину поверхні наведено на малюнку 3.1c.

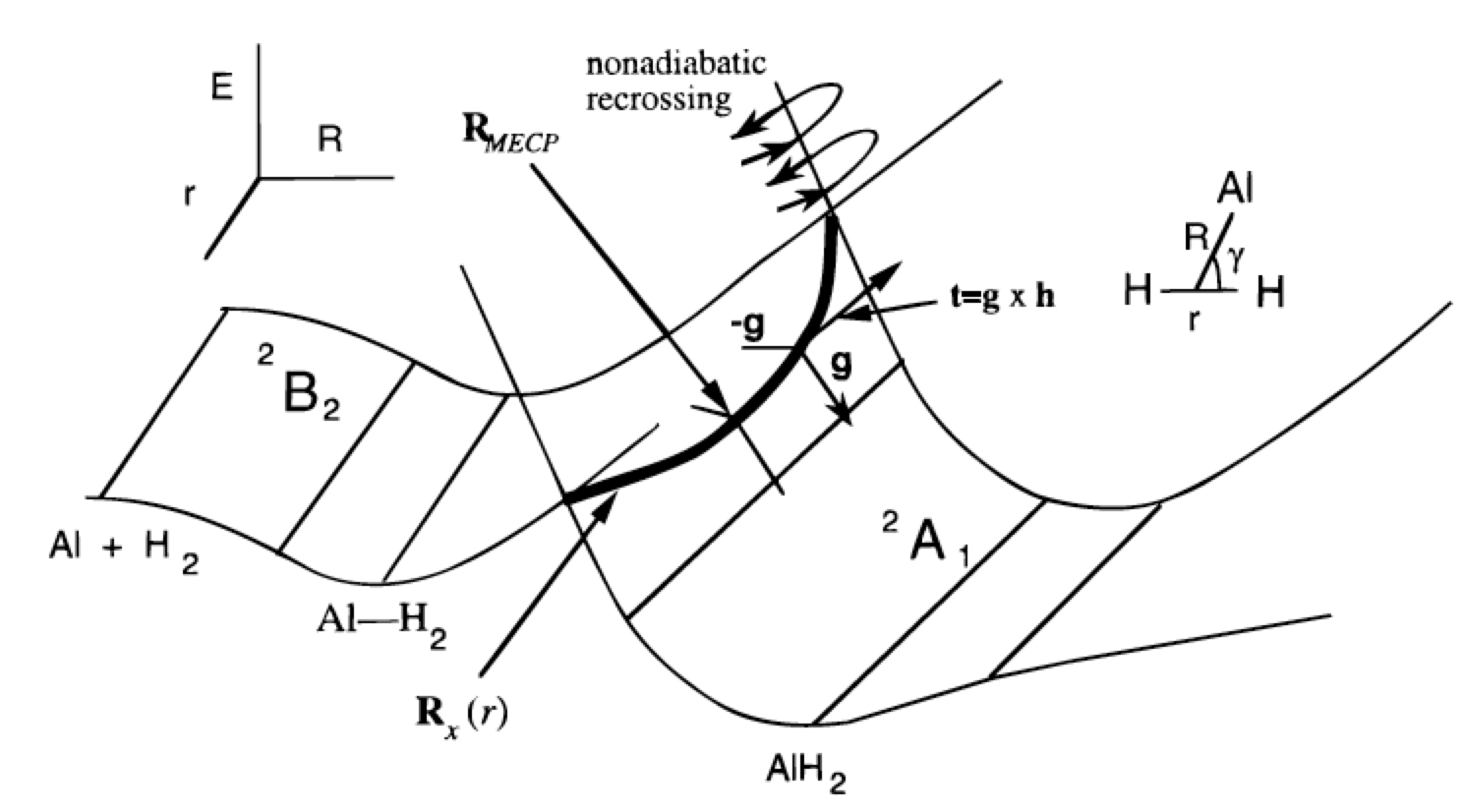
Малюнок 3.1c Зображення\(^2A_1\) поверхонь\(^2B_2\) Борна-Оппенгеймера, що виникають, коли Al (\(3s^2 3p^1; 2P\)) поєднується з\(H_2\)\((\sigma_g^2; ^1\Sigma_g^+)\) формою\(AlH_2(^2A_1)\).

Спочатку розглядаючи реакцію Al (3s2 3p1; 2P) з\(H_2 (sg2; 1Sg+)\) утворенням AlH2 (^ ^ 2A_1), як ніби вона відбулася в\(C_{2v}\) симетрії, зайнята 3p орбіталь\(Al\) атома може бути спрямована будь-яким із трьох способів.

Якщо він спрямований до середини зв'язку H-H, він створює електронний стан\(^2A_1\) симетрії.
Якщо вона спрямована з площини\(AlH_2\), то вона дає стан\(2B_1\) симетрії, і
якщо він спрямований паралельно H-H зв'язку, то він створює стан\(^2B_2\) симетрії.

\(^2A_1\)Стан, як показано у верхньому лівому куті малюнка 3.1c, відштовхуючий, оскільки 3s та 3p орбіталі атома Al починають перекриватися\(\sigma_g\) орбіталлю молекули водню при великих\(R\) -значеннях. \(^2B_2\)Стан, в якому зайнята орбіталь 3p спрямована вбік паралельно H-H зв'язку, призводить до неглибокої добре ван дер Ваальса на довгому R, але також рухається до більш високої енергії при коротших\(R\) -значеннях.

Основний стан\(AlH_2\) молекули має п'ять валентних орбіталей, зайнятих наступним чином:

два електрони займають зв'язок Al-H орбіталі\(a_1\) симетрії,
два електрони займають зв'язок Al-H орбіталі\(b_2\) симетрії, і
залишився електрон займає незв'язну орбіту\(sp^2\) характеру, локалізовану на атомі Al і має симетрію a1.

Ця\(a_1^2 b_2^2 a_1^1\) орбітальна заповненість основного стану\(AlH_2\) молекули не корелює безпосередньо з жодною з трьох вироджених конфігурацій основного стану\(Al + H_2\) якої є\(a_1^2 a_1^2 a_1^1, a_1^2 a_1^2 b_1^1\), і\(a_1^2 a_1^2 b_2^1\) як пояснювалося раніше. Саме ця відсутність прямої кореляції конфігурації породжує реакційний бар'єр шоу на малюнку 3.1c.

Давайте тепер повернемося до питання знаходження нижчевимірного (\(3N-8\)або\(3N-7\)) простору, в якому дві поверхні перетинаються, припускаючи, що одна має наявну інформацію про градієнти і Гессіани обох цих енергетичних поверхонь\(V_1\) і\(V_2\). Існує дві складові характеристики простору перетину, всередині яких\(V_1\) =\(V_2\):

Потрібно спочатку знайти одну геометрію,\(\textbf{q}_0\) що лежить у цьому просторі, а потім,
потрібно вибірки сусідніх геометрій (наприклад, які можуть мати меншу загальну енергію), що лежать у цьому підпросторі, де\(V_1 = V_2\).

Щоб знайти геометрію, при якій функція різниці\(F = [V_1 –V_2]^2\) проходить через нуль, можна використовувати звичайні методи функціональної мінімізації, такі як ті, які детально описані раніше при обговоренні того, як знайти енергетичні мінімуми\(F = 0\), знайти де, але тепер функція, яка прагне знайти мінімум на є різниця поверхні потенційної енергії.

Після того, як одна така геометрія\(\textbf{q}_0\) була розташована, згодом намагається слідувати шву (тобто для триатомної молекули це одновимірна лінія перетину; для більших молекул це\(3N-8\) розмірний простір), всередині якого функція\(F\) залишається нульовою. Професор Девід Ярконі розробив ефективні процедури для характеристики таких підпросторів (D.R. Yarkony, Acc. Хім. Рез. 31, 511-518 (1998)). Основна ідея полягає в параметризації кроків від (\(q_0\)) таким чином, щоб такі кроки не мали жодного компонента уздовж градієнта (\(H_{1,1} –H_{2,2}\)) або вздовж градієнта\(H_{1,2}\). Тому що\(V_1 = V_2\) вимагає наявності обох\(H_{1,1} = H_{2,2}\) і\(H_{1,2} = 0\), вжиття кроків, що підкоряються цим двом обмеженням, дозволяє залишатися в межах підпростору, де\(H_{1,1} = H_{2,2}\) і одночасно\(H_{1,2} = 0\) виконуються. Звичайно, це грізне завдання скласти карту всього\(3N-8\) або\(3N-7\) розмірного простору, всередині якого дві поверхні перетинаються, і цього, по суті, ніколи не робиться. Натомість зазвичай намагатися знайти, наприклад, точку в цьому підпросторі, в якій дві поверхні мають найнижчу енергію. Прикладом такої точки є маркування RMECP на малюнку 3.1c, і буде представляти особливий інтерес при вивченні реакцій, що відбуваються на поверхні з нижчою енергією, які мають доступ до шва, що перетинає поверхню, щоб еволюціонувати на верхню поверхню. Енергія в RMECP відображає найнижчу енергію, необхідну для доступу до цього перетину поверхні.

Такі процедури розташування швів перетину стають все більш поширеними, але все ще знаходяться в стадії дуже активної розробки, тому я зверну читача до наведеної вище статті професора Ярконя для подальшого керівництва. Наразі достатньо сказати, що розташування таких поверхневих перетинів є важливим інгредієнтом, коли хтось зацікавлений у вивченні, наприклад, фотохімічних реакцій, в яких реагенти та продукти можуть переміщатися з однієї електронної поверхні на іншу, або теплових реакцій, які вимагають від системи еволюціонування на збуджений стан через поверхневий перетин.

Кінцеві виноски

Це ряд геометрій,\(R_x\) визначених за допомогою лінійної інтерполяції (за допомогою параметра\(0 < x < 1\)) між\(3N\) декартовими координатами,\(R_{\rm reactants}\) що належать до рівноважної геометрії реагентів, та відповідними координатами\(R_{\rm products}\) продуктів:\(R_x = R_{\rm reactants} x + (1-x) R_{\rm products}\)