1.1: Чому потрібна квантова механіка
- Page ID
- 18946
Область теоретичної хімії займається структурами, зв'язком, реакційною здатністю та фізичними властивостями атомів, молекул, радикалів та іонів, розміри яких варіюються від ca. 1 Å для атомів і малих молекул до декількох сотень Å для полімерів та біологічних молекул, таких як ДНК та білки. Іноді ці будівельні блоки об'єднуються, утворюючи наноскопічні матеріали (наприклад, квантові точки, графенові листи), розміри яких охоплюють тисячі Å, що робить їх піддатними для виявлення за допомогою спеціалізованих мікроскопічних інструментів. Однак було виявлено, що опис рухів і властивостей частинок, що містять такі малі системи, не піддаються обробці за допомогою класичної механіки. Їх структури, енергії та інші властивості були успішно описані тільки в рамках квантової механіки. Ось чому квантову механіку потрібно освоювати як частину вивчення теоретичної хімії.
Ми знаємо, що всі молекули складаються з атомів, які, в свою чергу, містять ядра та електрони. Як я обговорюю в цьому розділі, рівняння, які керують рухами електронів та ядер, не є знайомими рівняннями Ньютона
\[\textbf{F} = m \textbf{a} \tag{1.1}\]
але новий набір рівнянь називається рівняннями Шредінгера. Коли вчені вперше вивчали поведінку електронів і ядер, вони намагалися інтерпретувати свої експериментальні знахідки з точки зору класичних ньютонівських рухів, але такі спроби врешті-решт провалилися. Вони виявили, що такі дрібні світлові частинки поводилися так, що просто не узгоджується з рівняннями Ньютона. Дозвольте мені зараз проілюструвати деякі експериментальні дані, які породили ці парадокси, і показати вам, як вчені тих ранніх часів тоді використовували ці дані, щоб запропонувати нові рівняння, яким ці частинки можуть підкорятися. Я хочу підкреслити, що рівняння Шредінгера не було виведено, а постульоване цими вченими. Насправді, на сьогоднішній день, наскільки мені відомо, ніхто не зміг вивести рівняння Шредінгера.
З новаторської роботи Брегга по дифракції рентгенівських променів від площин атомів або іонів в кристалах було відомо, що піки інтенсивності дифракційних рентгенівських променів, що мають довжину хвилі l, будуть виникати при кутах розсіювання q, визначених відомим рівнянням Брегга:
\[n \lambda = 2 d \sin{\theta} \tag{1.2}\]
де d - відстань між сусідніми площинами атомів або іонів. Ці величини проілюстровані на малюнку 1.1, показаному нижче. Існує безліч таких дифракційних піків, кожен з яких позначений різним значенням цілого числа\(n\) (\(n = 1, 2, 3, \cdots\)). Формулу Брегга можна вивести, враховуючи, коли два фотони, один розсіює з другої площини на малюнку і другий розсіює з третьої площини, зазнають конструктивної інтерференції. Ця умова виконується, коли додаткова довжина шляху, покрита другим фотоном (тобто довжина від точок\(A\)\(B\) до\(C\)), є цілим числом кратним довжині хвилі фотонів.
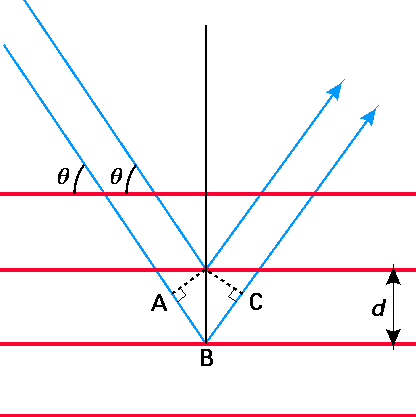
Значення цих експериментів з розсіювання рентгенівських променів для електронів і ядер з'являється в експериментах Девіссона і Гермера в 1927 році, які розсіяли електрони (розумно) фіксованої кінетичної енергії\(E\) з металевих кристалів. Ці працівники виявили, що ділянки кількості розсіяних електронів як функція кута розсіювання\(\theta\) відображали піки під кутами\(\theta\), які підкорялися рівнянню Брагга. Вражаюча річ у цьому спостереженні полягає в тому, що електрони є частинками, але рівняння Брегга базується на властивостях хвиль. Важливим спостереженням, отриманим з експериментів Девіссона-Гермера, було те, що кути розсіювання, що\(\theta\) спостерігаються для електронів кінетичної енергії,\(E\) можуть відповідати рівнянню Брегга, якщо до цих електронів приписувалася довжина хвилі, яка була визначена
\[\lambda = \dfrac{h}{\sqrt{2m_e E}} \tag{1.3}\]
де\(m_e\) - маса електрона, а h - константа, введена Максом Планком і Альбертом Ейнштейном на початку 1900-х років, щоб пов'язати енергію\(E\) фотона з його частотою\(E = h\nu\) (\(\nu\)через). Ці дивовижні знахідки були одними з перших, щоб припустити, що електрони, які завжди розглядалися як частинки, можуть мати деякі властивості, які зазвичай приписують хвилям. Тобто, як запропонував де Брольє в 1925 році, електрон, здається, має довжину хвилі, обернено пов'язану з його імпульсом, і відображає дифракцію хвильового типу. Слід зазначити, що аналогічна дифракція спостерігалася і тоді, коли інші дрібні частинки світла (наприклад, протони, нейтрони, ядра та малі атомні іони) були розсіяні з кристалічних площин. У всіх таких випадках спостерігається дифракція, подібна до Брегга, і встановлено, що рівняння Брегга регулює кути розсіювання, якщо призначити довжину хвилі частинці розсіювання відповідно до
\[\lambda = \dfrac{h}{\sqrt{2m E}} \tag{1.4}\]
де
- \(m\)це маса розсіяної частинки і
- \(h\)є постійною Планка (6,62 х10 -27 ерг сек).
Спостереження за тим, що електрони та інші дрібні частинки світла відображають хвильову поведінку, було важливим, оскільки ці частинки - це те, з чого складаються всі атоми та молекули. Отже, якщо ми хочемо повністю зрозуміти рухи і поведінку молекул, ми повинні бути впевнені, що зможемо адекватно описати такі властивості для їх складових. Оскільки класичні ньютонівські рівняння не містять факторів, які передбачають хвильові властивості електронів або ядер, що вільно рухаються у просторі, вищевказана поведінка представляла значні проблеми.
Ще одна проблема, яка виникла в ранніх дослідженнях атомів і молекул, виникла в результаті вивчення фотонів, що виділяються атомами та іонами, які були нагріті або іншим чином збуджені (наприклад, електричним розрядом). Встановлено, що кожен вид атомів (тобто H або C або O) випромінював фотони, частоти яких\(\nu\) мали дуже характерні значення. Приклад таких спектрів випромінювання показаний на малюнку 1.2 для атомів водню.
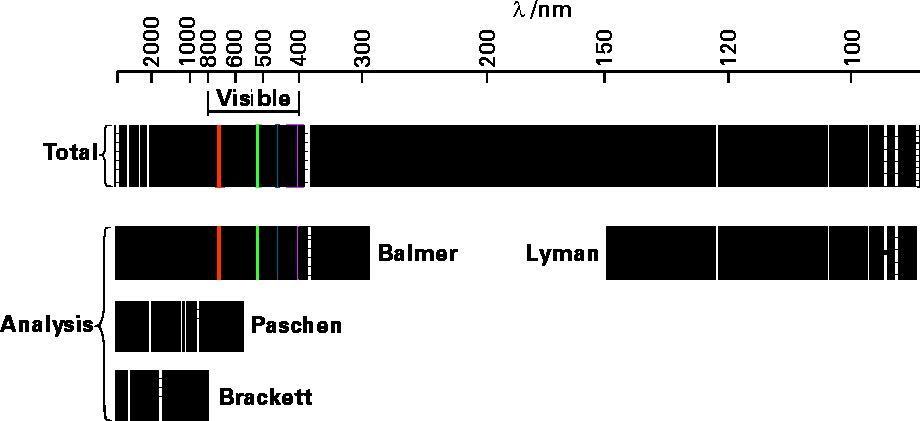
На верхній панелі ми бачимо всі лінії, випромінювані з їх довжинами хвиль, вказаними в нанометрах. Інші панелі показують, як ці лінії були проаналізовані (вченими, чиї імена пов'язані) на закономірності, які стосуються конкретних енергетичних рівнів, між якими відбуваються переходи для випромінювання відповідних фотонів.
У перших спробах раціоналізувати такі спектри з точки зору електронних рухів, один описував електрон як рухається навколо атомних ядер по кругових орбітах, як показано на малюнку 1.3.

Кругова орбіта вважалася стабільною, коли зовнішня відцентрова сила, що характеризується радіусом\(r\) і швидкістю\(v\) (\(m_e v^2/r\)) на електроні, ідеально врівноважує внутрішню привабливу кулонівську силу (\(Ze^2/r^2\)), що чиниться ядром заряду\(Z\):
\[m_e \dfrac{v^2}{r} = \dfrac{Ze^2}{r^2} \tag{1.5}\]
Це рівняння, в свою чергу, дозволяє пов'язати кінетичну енергію\(\dfrac{1}{2} m_e v^2\) з кулонівської енергією\(Ze^2/r\), і таким чином висловити загальну енергію\(E\) орбіти через радіус орбіти:
\[E = \dfrac{1}{2} m_e v^2 – \dfrac{Ze^2}{r^2} = -\dfrac{1}{2} \dfrac{Ze^2}{r^2} \tag{1.6}\]
Енергія, що характеризує орбіту або радіус\(r\), щодо\(E = 0\) еталонної енергії при\(r \rightarrow \infty\), стає все більш негативною (тобто нижчою і нижчою) у міру того, як\(r\) стає менше. Цей зв'язок між зовнішніми і внутрішніми силами дозволяє зробити висновок, що електрон повинен рухатися швидше, коли він рухається ближче до ядра з тих пір\(v^2 = Ze^2/(r m_e)\). Однак ніде в цій моделі немає поняття, яке відноситься до експериментального факту, що кожен атом випромінює тільки певні види фотонів. Вважалося, що випромінювання фотонів відбувалося, коли електрон, що рухається по більшій кругової орбіті, втратив енергію і перемістився на меншу кругову орбіту. Однак динаміка Ньютона, яка виробляла вищевказане рівняння, дозволила б слідувати орбітам будь-якого радіуса, а отже, і будь-якої енергії. Таким чином, здавалося б, електрон повинен мати можливість випромінювати фотони будь-якої енергії при переміщенні з орбіти на орбіту.
Прорив, який дозволив таким вченим, як Нільс Бор, застосувати модель кругової орбіти до спостережуваних спектральних даних, передбачав спочатку введення ідеї про те, що електрон має довжину хвилі і що ця довжина хвилі l пов'язана з його імпульсом рівняння де Броля\(\lambda = h/p\). Ключовим кроком у моделі Бора було також вказати, що радіус кругової орбіти бути таким, щоб окружність кола\(2\pi r\) дорівнювала цілому (\(n\)) кратному довжині хвилі\(\lambda\). Тільки таким чином хвиля електрона зазнає конструктивної інтерференції, коли електрон обертається навколо ядра. Таким чином, зв'язок Бора, аналогічний рівнянню Брегга, що визначає, під якими кутами можуть виникати конструктивні перешкоди, є
\[2 \pi r = n \lambda. \tag{1.7}\]
І це рівняння, і аналогічне рівняння Брегга є ілюстраціями того, що ми називаємо граничними умовами; вони є додатковими умовами, розміщеними на довжині хвилі для отримання певного бажаного символу в результуючій хвилі (у цих випадках конструктивної інтерференції). Звичайно, залишається питання про те, навіщо нав'язувати ці зайві умови, коли динаміка Ньютона їх не вимагає. Дозвіл цього парадоксу - одна з речей, які робить квантова механіка.
Повертаючись до наведеного вище аналізу та використовуючи\(\lambda = h/p = h/(m_e v)\)\(2\pi r = n\lambda\), а також рівняння сили та балансу\(m_e v^2/r = Ze^2/r^2\), можна потім вирішити для радіусів, яким підкоряються стабільні орбіти Бора:
\[r = \left(\dfrac{nh}{2\pi}\right)^2 \dfrac{1}{m_e Z e^2} \tag{1.8}\]
і, в свою чергу, для швидкостей електронів на цих орбітах
\[v = \dfrac{Z e^2}{nh/2\pi}. \tag{1.9}\]
Ці два результати дозволяють висловити суму кінетичної (\(\dfrac{1}{2} m_e v^2\)) та кулонівського потенціалу (\(-Ze^2/r\)) енергій як
\[E = -\dfrac{1}{2} m_e Z^2 \dfrac{e^4}{(nh/2\pi)^2}. \tag{1.10}\]
Так само, як і в результаті дифракції Брегга, який вказував, під якими кутами відбувалися особливі високі інтенсивності розсіювання, існує багато стійких орбіт Бора, кожна з яких позначена значенням цілого числа\(n\). Ті,\(n\) у кого малі, мають малі радіуси (масштабування як\(n^2\)), високі швидкості (масштабування як 1/n) і більше негативних сумарних енергій (n.b., опорний нуль енергії відповідає електрону при\(r = \infty\), а з\(v = 0\)). Отже, це результат того, що допускаються лише певні орбіти, що спричиняє виникнення лише певних енергій і, таким чином, лише певних енергій, які слід спостерігати в випромінюваних фотонах.
Виявилося, що формула Бора для енергетичних рівнів (маркованих\(n\)) електрона, що рухається навколо ядра, може бути використана для пояснення дискретних лінійних спектрів випромінювання всіх одноелектронних атомів і іонів (тобто\(H\)\(He^+\),\(Li^{+2}\), і т.д., іноді називають гідрогенними видами) до дуже висока точність. У такій інтерпретації експериментальних даних стверджується, що фотон енергії
\[h\nu = R \left(\dfrac{1}{n_i^2} – \dfrac{1}{n_f^2}\right) \tag{1.11}\]
випромінюється, коли атом або іон зазнає переходу від орбіти, що має квантове число,\(n_i\) до орбіти нижчої енергії, що має\(n_f\). Тут символ\(R\) використовується для позначення наступної сукупності факторів:
\[R = \dfrac{1}{2} m_e Z^2 \dfrac{e^4}{\Big(\dfrac{h}{2\pi}\Big)^2} \tag{1.12}\]
і називається одиницею енергії Рідберга і дорівнює 13,6 еВ.
Формула Бора для енергетичних рівнів також не узгоджувалася із спостережуваною схемою спектрів випромінювання для видів, що містять більше одного електрона. Однак це дає розумну відповідність, наприклад, спектрам атома Na, якщо досліджувати лише переходи, що беруть участь лише один 3s валентний електрон. Більше того, це може бути значно покращено, якщо ввести модифікацію, призначену для лікування проникнення 3s та вищих орбіталів атома Na в межах областей простору, зайнятих орбіталями 1s, 2s та 2p. Така модифікація моделі Бора досягається шляхом введення ідеї так званого квантового дефекту d в основне квантове число\(n\) таким чином, що вираз для\(n\) -залежності орбіталей змінюється на
\[E = \dfrac{-R}{(n-\delta)^2} \tag{1.13}\]
| Приклад 1.1 |
|---|
|
Наприклад, вибравши\(\delta\) рівне 0,41, 1,37, 2,23, 3,19 або 4,13 для Li, Na, K, Rb і Cs відповідно, в цій так званій формулі Рідберга, можна знайти гідну згоду між\(n\) -залежністю енергетичних інтервалів одиночно збуджених валентних станів цих атомів. Той факт,\(\delta\) що більший для Na, ніж для Li і найбільший для Cs відображає той факт, що 3s орбіталь Na проникає в оболонки 1s, 2s та 2p, тоді як 2s орбіталь Li проникає лише в оболонку 1s, а орбіталь 6s Cs проникає в оболонки\(n = \) 1, 2, 3, 4 та 5. |
Виявляється, ця формула Рідберга може бути застосована і до певних електронних станів молекул. Зокрема, для катіонів із закритою оболонкою\(NH_4^+\)\(H_3O^+\), таких як протоновані спирти та протоновані аміни (навіть на бічних ланцюгах амінокислот), електрон може бути приєднаний до так званої орбіталі Рідберга для утворення відповідних нейтральних радикалів, таких як\(NH_4\)\(H_3O\),,\(R-NH_3\), або \(R-OH_2\). Наприклад, в\(NH_4\), електрон пов'язаний з підлеглим\(NH_4^+\) катіонним ядром. Найнижчий енергетичний стан цього виду Рідберга часто позначається на 3s, оскільки\(NH_4^+\) є ізоелектронним з катіоном Na+, який зв'язує електрон у своїй 3s орбіталі в основному стані. Як і у випадку з атомами лугу, ці молекули Рідберга також володіють збудженими електронними станами. Наприклад, радикал NH4 має стани з позначкою 3p, 3d, 4s, 4p, 4d, 4f і т.д. зробивши відповідний вибір параметра квантового дефекту d, енергетичні відстані між цими станами можуть бути досить добре підігнані до формули Рідберга (Рівняння 1.13). На малюнку 1.3.a показано кілька орбіталів\(NH_4\) Рідберга
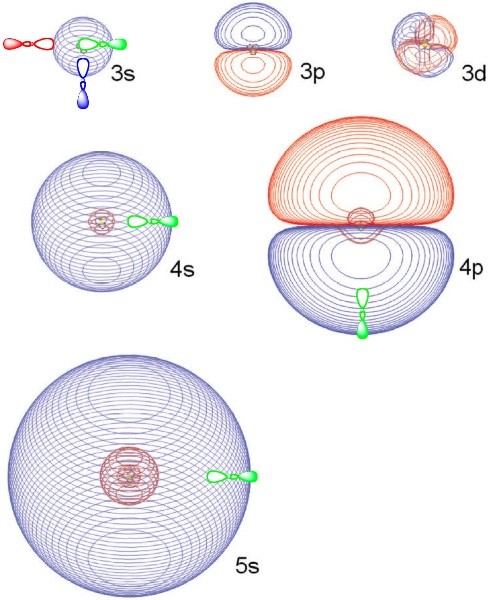
Ці орбіталі Рідберга можуть бути досить великими (їх розміри масштабуються так само\(n^2\), чітко мати s, p або d кутові форми, і володіти очікуваною кількістю радіальних вузлів. Однак для молекулярних орбіталів Рідберга, і на відміну від атомних орбіталів Рідберга, три\(p\), п'ять\(d\)\(f\), сім і т.д. орбіталі не вироджуються; натомість вони розщеплюються енергією таким чином, що відображає симетрію симетрії основного катіона. Наприклад, для\(NH_4\), три\(3p\) орбіталі вироджені і належать до\(t_2\) симетрії в\(T_d\) точковій групі; п'ять\(3d\) орбіталів розділені на три вироджені\(t_2\) і дві вироджені e орбіталі.
Так, модель Бора добре працює для одноелектронних атомів або іонів, а квантове модифіковане дефектом рівняння Бора досить добре описує деякі стани атомів лугу та молекул Рідберга. Основною причиною пробою формули Бора є нехтування електронно-електронними кулонівськими відштовхуваннями при її виведенні, які якісно коригуються за допомогою квантового параметра дефекту атомів і молекул Рідберга. Проте успіх моделі Бора дав зрозуміти, що дискретні спектри випромінювання можна пояснити лише введенням концепції, що дозволені не всі орбіти. Тільки спеціальні орбіти, які підкорялися конструктивно-інтерференційній умові, були дійсно доступні рухам електрона. Ця ідея про те, що не всі енергії були дозволені, але можуть відбуватися лише певні квантовані енергії, мала важливе значення для досягнення навіть якісного почуття згоди з експериментальним фактом, що спектри випромінювання були дискретними.
Таким чином, двома експериментальними спостереженнями щодо поведінки електронів, які мали вирішальне значення для відмови від ньютонівської динаміки, були спостереження дифракції електронів та спектрів дискретних емісій. Обидва ці висновки, здається, припускають, що електрони мають деякі хвильові характеристики і що ці хвилі мають лише певні дозволені (тобто квантовані) довжини хвиль.
Отже, тепер ми маємо деяке уявлення про те, чому рівняння Ньютона не враховують динамічних рухів світла та дрібних частинок, таких як електрони та ядра. Ми бачимо, що додаткові умови (наприклад, умова Брегга або обмеження на довжину хвилі де Броля) можуть бути накладені для досягнення певної міри згоди з експериментальним спостереженням. Однак нам все ще залишається цікаво, які рівняння можуть бути застосовані для правильного опису таких рухів і навіщо потрібні додаткові умови. Виявляється, для вирішення таких питань потрібно було розробити новий вид рівняння, заснованого на поєднанні хвильових і частинок властивостей. Це так звані рівняння Шредінгера, на які ми зараз звернемо свою увагу.
Як я вже говорив раніше, ніхто ще не показав, що рівняння Шредінгера випливає з деякої більш фундаментальної теорії. Тобто вчені не вивели цього рівняння, вони постулювали його. Деяке уявлення про те, як вчені тієї епохи придумали рівняння Шредінгера, можна мати, вивчивши часову та просторову залежність, яка характеризує так звані біжучі хвилі. Слід зазначити, що люди, які працювали над цими проблемами, знали багато про хвилі (наприклад, звукові хвилі та водні хвилі) та рівняння, які вони підкорялися. Більше того, вони знали, що хвилі іноді можуть відображати характеристику квантованих довжин хвиль або частот (наприклад, основи та обертони у звукових хвиль). Вони знали, наприклад, що хвилі в одному вимірі, які обмежені в двох точках (наприклад, скрипка струна, закріплена на двох кінцях) зазнають коливального руху в просторі і часі з характерними частотами і довжинами хвиль. Наприклад, рух щойно згаданої скрипичної струни можна охарактеризувати як має амплітуду\(A(x,t)\) в положенні\(x\) уздовж її довжини в той час, що\(t\) задається
\[A(x,t) = A(x,o) \cos(2\pi \nu t), \tag{1.14}\]
де\(nu\) - частота його коливань. Просторова залежність амплітуди також має синусоїдальну залежність, задану
\[A(x,0) = A \sin (\dfrac{2\pi x}{\lambda}) \tag{1.15}\]
де\(\lambda\) - довжина хвилі від гребеня до гребеня. Два приклади таких хвиль в одному вимірі наведені на малюнку 1.4.
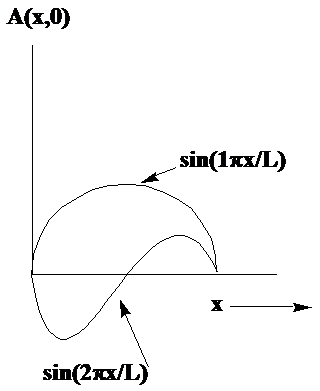
У цих випадках струна фіксується в\(x = 0\) і в\(x = L\), тому довжини хвиль, що належать двом показаним хвилям, є\(\lambda = 2L\) і\(\lambda = L\). Якби струна скрипки не була затиснута\(x = L\), хвилі могли мати будь-яке значення\(\lambda\). Однак, оскільки рядок прикріплений на\(x = L\), дозволені довжини хвиль квантуються, щоб підкорятися
\[\lambda = \dfrac{2L}{n}, \tag{1.16}\]
де\(n = 1, 2, 3, 4, \cdots\). Рівняння, якому підкоряються такі хвилі, називається хвильовим рівнянням, говорить:
\[\dfrac{d^2A(x,t)}{dt^2} = c^2 \dfrac{d^2A}{dx^2} \tag{1.17}\]
де\(c\) швидкість, з якою рухається хвиля. Ця швидкість залежить від складу матеріалу, з якого виготовлена струна скрипки; жорсткий струнний матеріал виробляє хвилі з більшими швидкостями, ніж для більш м'якого матеріалу. Використовуючи більш ранні вирази для\(x-\) і\(t\) -залежностей хвилі\(A(x,t)\), ми знаходимо, що частота і довжина хвилі пов'язані так званим дисперсійним рівнянням:
\[\nu^2 = \left(\dfrac{c}{\lambda}\right)^2, \tag{1.18}\]
або
\[c = \lambda \nu. \tag{1.19}\]
Цей зв'язок передбачає, наприклад, що струна приладу, виготовлена з дуже жорсткого матеріалу (великого\(c\)), буде виробляти більш високий частотний тон для заданої довжини хвилі (тобто заданого значення\(n\)), ніж струна, виготовлена з більш м'якого матеріалу (меншого розміру\(c\)).
Для хвиль, що рухаються по поверхні, наприклад, прямокутної двомірної поверхні довжин\(L_x\) і\(L_y\), можна знайти
\[A(x,y,t) = \sin \left(n_x \dfrac{p_x}{L_x}\right) \sin\left(n_y \dfrac{p_y}{L_y}\right) \cos\left(2\pi \nu t\right). \tag{1.20}\]
Отже, хвилі квантуються у двох вимірах, оскільки їх довжини хвиль повинні бути обмежені,\(A(x,y,t)\) щоб призвести до зникнення,\(x = 0\) а\(x = L_x\) також у\(y = 0\) та\(y = L_y\) назавжди\(t\).
Важливо зазначити, закриваючи це обговорення хвиль на струні та поверхнях, що це не є рішенням рівняння Шредінгера, що призводить до квантування довжин хвиль. Натомість це умова, що хвиля зникає на кордоні, що породжує квантування. Ви побачите цю тенденцію знову і знову у всьому цьому тексті; коли хвильова функція піддається конкретним обмеженням на її внутрішній або зовнішній межі (або обох), квантування призведе; якщо цих граничних умов немає, квантування не відбудеться. Повернемося тепер до питання хвиль, які описують електрони, що рухаються.
Піонери квантової механіки досліджували функціональні форми, подібні до наведених вище. Наприклад, такі форми, як\(A = \exp[\pm 2\pi(\nu t – x/\lambda)]\) розглядалися, оскільки вони відповідають періодичним хвилям, які еволюціонують у зовнішніх\(x\) - або\(t\) -залежних силах\(x\) і не\(t\) під ними. Помітивши, що
\[\dfrac{d^2A}{dx^2} = - \left(\dfrac{2\pi}{\lambda} \right)^2 A \tag{1.21}\]
і використовуючи гіпотезу де Бройля\(\lambda = h/p\) у вищевказаному рівнянні, можна знайти
\[\dfrac{d^2A}{dx^2} = - p^2 \Big(\dfrac{2\pi}{h}\Big)^2 A. \tag{1.22}\]
Якщо\(A\) передбачається відношення до руху частинки імпульсу p при відсутності зовнішніх сил (так як форма хвилі відповідає цьому випадку),\(p^2\) може бути пов'язана з\(E\) енергією частинки по\(E = p^2/2m\). Отже, рівняння для\(A\) можна переписати так:
\[\dfrac{d^2A}{dx^2} = - 2m E \Big(\dfrac{2\pi}{h}\Big)^2 A, \tag{1.23}\]
або, як варіант,
\[- \Big(\dfrac{h}{2\pi}\Big)^2 (\dfrac{1}{2}m) \dfrac{d^2A}{dx^2} = E A. \tag{1.23}\]
Повертаючись до часової залежності\(A(x,t)\) та використання\(\nu = E/h\), можна також показати, що
\[i \Big(\dfrac{h}{2\pi}\Big) \dfrac{dA}{dt} = E A, \tag{1.24}\]
який, використовуючи перший результат, говорить про те, що
\[i \Big(\dfrac{h}{2\pi}\Big) \dfrac{dA}{dt} = - \Big(\dfrac{h}{2\pi}\Big)^2 (\dfrac{1}{2}m) \dfrac{d^2A}{dx^2}. \tag{1.25}\]
Це примітивна форма рівняння Шредінгера, про яку ми розглянемо набагато докладніше нижче. Коротко, що важливо мати на увазі, що використання зв'язків де Броґлі та Планка/Ейнштейна (\(\lambda = h/p\)і\(E = h\nu\)), обидва з яких включають постійну h, виробляє сугестивні зв'язки між
\[i \Big(\dfrac{h}{2\pi}\Big) \dfrac{d}{dt} \text{ and } E \tag{1.26}\]
і між
\[p^2 \text {and } – \Big(\dfrac{h}{2\pi}\Big)^2 \dfrac{d^2}{dx^2} \tag{1.27}\]
або, як варіант, між
\[p \text{ and } – i \Big(\dfrac{h}{2\pi}\Big) \dfrac{d}{dx}.\tag{1.28}\]
Ці зв'язки між фізичними властивостями (енергією\(E\) та імпульсом\(p\)) та диференціальними операторами є одними з незвичайних особливостей квантової механіки.
Вищезазначене обговорення хвиль та квантованих довжин хвиль, а також спостереження щодо хвильового рівняння та диференціальних операторів не мають на меті забезпечити або навіть запропонувати виведення рівняння Шредінгера. Знову вчені, які винайшли квантову механіку, не вивели її робочих рівнянь. Натомість рівняння та правила квантової механіки були постульовані та розроблені таким чином, щоб відповідати лабораторним спостереженням. Мої студенти часто вважають, що це бентежить, оскільки вони сподіваються і шукають основну фундаментальну основу, з якої логічно слідують основні закони квантової механіки. Я намагаюся нагадати їм, що теорія працює не так. Натомість один використовує експериментальне спостереження постулювати правило або рівняння або теорію, а потім перевіряє теорію, роблячи прогнози, які можуть бути перевірені подальшими експериментами. Якщо теорія зазнає невдачі, її потрібно вдосконалити, і цей процес триває, поки не з'явиться краща і краща теорія. У цьому сенсі квантову механіку з усіма її незвичайними математичними конструкціями та правилами слід розглядати як випливає з уяви вчених, які намагалися винайти теорію, яка відповідала експериментальним даними і яку можна було б використовувати для прогнозування речей, які потім можна було б перевірити в лабораторії. . До цих пір ця теорія виявилася надійною, але, звичайно, ми завжди шукаємо нову вдосконалену теорію, яка описує, як рухаються дрібні частинки світла.
Якщо це допоможе вам більше сприймати квантову теорію, я повинен зазначити, що квантовий опис частинок зводиться до класичного опису Ньютона за певних обставин. Зокрема, при лікуванні важких частинок (наприклад, макроскопічних мас і навіть більш важких атомів) часто можна використовувати динаміку Ньютона. Незабаром ми більш детально обговоримо, як іноді збігаються квантова і класична динаміка (в цьому випадку можна вільно використовувати більш просту динаміку Ньютона). Отже, давайте тепер перейдемо до цього дивного рівняння Шредінгера, про яке ми так довго відволікаємося.
