11.13: Абсолютний нуль недосяжний

Третій закон постулює, що ентропія речовини завжди кінцева і що вона наближається до постійної, коли температура наближається до нуля. Значення цієї константи не залежить від значень будь-яких інших функцій стану, які характеризують речовину. Для будь-якої даної речовини ми можемо привласнити довільно вибране значення граничному значенню нульової температури. Однак ми не можемо призначити довільні ентропії з нульовою температурою всім речовинам. Набір завдань, які ми робимо, повинен відповідати експериментально спостережуваним граничним значенням нульової температури ентропійних змін реакцій між різними речовинами. Для ідеально кристалічних речовин ці реакційні ентропії все дорівнює нулю. Ми можемо задовольнити цю умову, присвоївши довільне значення молярній ентропії кожного елемента з нульовою температурою і обумовивши, що ентропія будь-якої сполуки з нульовою температурою є сумою нульових температурних ентропій його складових елементів. Цей розрахунок значно спрощується, якщо ми дозволимо нульовій температурі ентропії кожного елемента дорівнювати нулю. Це істотний зміст третього закону.

Оператор Льюїса та Рендалла включає цей вибір опорного стану нульової ентропії для ентропій, вказуючи його як «кристалічний стан» кожного елемента при нульових градусах. В результаті ентропія будь-якої речовини при нульових градусах більше або дорівнює нулю. Тобто заява Льюїса і Рендалла включає в себе умовність, яка фіксує граничне значення нульової температури ентропії будь-якої речовини. У цьому відношенні заява Льюїса і Рендалла робить по суті довільний вибір, який не є власною властивістю природи. Однак ми бачимо, що це надзвичайно зручний вибір.

Ми обговорили альтернативні твердження першого та другого законів. Можливий і ряд альтернативних тверджень третього закону. Розглянемо наступне:

Неможливо домогтися температури абсолютного нуля.

Це твердження є більш загальним, ніж заява Льюїса і Рендалла. Якщо розглядати застосування цього твердження до температур, досяжних в процесах, що включають одну речовину, ми можемо показати, що воно має на увазі і мається на увазі твердження Льюїса і Рендалла.

Властивості теплоємності\(C_P\), відіграють центральну роль в цих аргументах. Ми бачили, що\(C_P\) це функція температури. Хоча це не корисно робити, ми можемо застосувати визначальне відношення\(C_P\) до речовини, що переживає фазовий перехід, і знайти\(C_P=\infty\). Якщо ми думаємо про речовину, теплоємність якої менше нуля, ми стикаємося з протиріччям наших основних уявлень про тепло\(q>0\) і температуру: якщо і\({q}/{\Delta T}<0\), ми повинні мати\(\Delta T<0\); тобто нагрівання речовини призводить до зниження її температури. Коротше кажучи, розроблена нами теорія вбудовує приміщення, які вимагають\(C_P>0\) для будь-якої системи, за якою ми можемо проводити вимірювання.

Охарактеризуємо систему з чистою речовиною за її тиском і температурою і розглянемо оборотні процеси постійного тиску, в яких можлива лише робота тиску — об'єму. Потім\({\left({\partial S}/{\partial T}\right)}_P={C_P}/{T}\) і\(dS={C_PdT}/{T}\). Зараз ми хочемо показати: умова Льюїса і Рендалла про те, що ентропія завжди кінцева, вимагає, щоб теплоємність йшла до нуля, коли температура йде до нуля. (Оскільки ми збираємося показати, що третій закон забороняє вимірювання при абсолютному нулі, цей висновок узгоджується з нашим висновком у попередньому пункті.) Те, що теплоємність йде до нуля, коли температура йде до нуля, видно з\(S={C_PdT}/{T}.\) Якщо\(C_P\) не йде до нуля, коли температура йде до нуля,\(dS\) стає довільно великою, оскільки температура йде до нуля, що суперечить твердженню Льюїса і Рендалла.

Щоб розвинути цей результат більш явно, ми дозволяємо теплові потужності при температурах\(T\) і нуль бути\(C_P\left(T\right)\) і\(C_P\left(0\right)\), відповідно. Так як\(C_P\left(T\right)>0\) для будь-якого\(T\ >\ 0\), у нас є\(S\left(T\right)-S\left(T^*\right)>0\) для будь-якого\(T>T^*>0\). Так як ентропія завжди кінцева\(\infty >S\left(T\right)-S\left(T^*\right)>0\), так що

\[\infty >{\mathop{\mathrm{lim}}_{T^*\to 0} \left[S\left(T\right)-S\left(T^*\right)\right]\ }>0\]

і

\[\infty >{\mathop{\mathrm{lim}}_{T^*\to 0} \int^T_{T^*}{\frac{C_P}{T}}\ }dT>0\]

Для температур в районі нуля ми можемо розширити теплоємність, до довільної точності, як поліном ряду Тейлора в\(T\):

\[C_P\left(T\right)=C_P\left(0\right)+\left(\frac{\partial C_P\left(0\right)}{\partial T}\right)_PT +\frac{1}{2} \left(\frac{{\partial }^2C_P\left(0\right)}{\partial T^2}\right)_PT^2+\dots \]

Нерівності стають

\[\infty >{\mathop{\mathrm{lim}}_{T^*\to 0} \left\{C_P\left(0\right){ \ln \frac{T}{T^*}\ }+{\left(\frac{\partial C_P\left(0\right)}{\partial T}\right)}_P\left(T-T^*\right)+\frac{1}{4}{\left(\frac{{\partial }^2C_P\left(0\right)}{\partial T^2}\right)}_P{\left(T-T^*\right)}^2+\dots \right\}\ }>0\]

Стан зліва вимагає\(C_P\left(0\right)=0\).

Третій закон ми могли б розглядати як твердження про теплоємності чистих речовин. Ми робимо висновок не тільки про те, що\(C_P>0\) для всіх\(T>0\), але і що

\[{\mathop{\mathrm{lim}}_{T\to 0} \left(\frac{C_P}{T}\right)=0\ }\]

Більш загально, ми можемо зробити висновок про відповідні твердження для закритих оборотних систем, які не є чистими речовинами:\({\left({\partial H}/{\partial T}\right)}_P>0\) для всіх\(T>0\), і\({\mathop{\mathrm{lim}}_{T\to 0} T^{-1}{\left({\partial H}/{\partial T}\right)}_P=0\ }\). (Однак ентропії з нульовою температурою таких систем не дорівнюють нулю.) В обговоренні нижче ми опишемо систему як чисту речовину. Ми можемо зробити по суті однакові аргументи для будь-якої системи; нам потрібно лише замінити\(C_P\) на\({\left({\partial H}/{\partial T}\right)}_P\). Твердження Льюїса і Рендалла стверджує, що ентропія йде в константу при абсолютному нулі, незалежно від значень будь-яких інших термодинамічних функцій. Звідси випливає, що ентропія при нулі градусів не залежить від величини тиску. Для будь-яких двох тисків,\(P_1\) і\(P_2\), у нас є\(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). Відпускаючи\({P=P}_1\)\(P_2=P+\Delta P\) і і, у нас є

\[\frac{S\left(P+\Delta P,0\right)-S\left(P,0\right)}{\Delta P}=0\]

для будь-якого\(\Delta P\). Отже, ми маємо

\[{\left(\frac{\partial S}{\partial P}\right)}_{T=0}=0\]

У главі 10 ми знаходимо\({\left({\partial S}/{\partial }P\right)}_T=-{\left({\partial V}/{\partial T}\right)}_P\), тому і ентропія, і об'єм наближаються до своїх значень нульової температури асимптотично.

Коли ми говоримо, що абсолютний нуль недосяжний, ми маємо на увазі, що жодна система не може зазнати будь-яких змін, в яких її кінцева температура дорівнює нулю. Щоб зрозуміти, чому абсолютний нуль повинен бути недосяжним, розглянемо процеси, які можуть знизити температуру системи. Загалом, у нас є теплові резервуари, доступні при різних температурах. Ми можемо вибрати наявний резервуар, температура якого найнижча, і довести систему до цієї температури простим тепловим контактом. Це багато тривіально; очевидно, завдання полягає в тому, щоб знизити температуру далі. Для цього ми повинні внести деякі інші зміни. Якою б не була ця зміна, їй не може сприяти обмін теплом з навколишнім середовищем. Після того, як ми довели систему до температури найхолоднішої доступної частини навколишнього середовища, будь-який подальший обмін теплом з навколишнім середовищем може бути лише контрпродуктивним. Ми робимо висновок, що будь-який процес, який відповідає нашій меті, повинен бути адіабатичним. Оскільки адіабатичний процес не обмінюється теплом з навколишнім середовищем,\(\Delta \hat{S}=0\).

Процес також повинен бути можливим процесом, так що\(\Delta S+\Delta \hat{S}\ge 0\), і оскільки він адіабатичний,\(\Delta S\ge 0\). Розглянемо оборотний процес і незворотний процес, при якому одна і та ж система\({}^{2}\) переходить від стану, заданого\(P_1\) і\(T_1\) до другого стану, в якому знаходиться тиск\(P_2\). Кінцеві температури і ентропійні зміни цих процесів різні. Для оборотного процесу,\(\Delta S=0\); кінцеву температуру ми позначаємо як\(T_2\). Для незворотного процесу,\(\Delta S>0\); кінцеву температуру ми позначаємо як\(T^*_2\). Як виявляється, зміна температури менше для незворотного процесу, ніж для оборотного процесу; тобто\(T_2-T_1<t^*_2-t_1\) >. Аналогічно, оборотний процес досягає нижчої температури:\({T_2<t}^*_2\) >. Від

\[dS=\frac{C_P}{T}dT-{\left(\frac{\partial V}{\partial T}\right)}_PdP\]

ми можемо обчислити зміни ентропії для цих процесів. Для оборотного процесу розраховуємо\[\Delta S^{rev}=S\left(P_2,T_2\right)-S\left(P_1,T_1\right)\]

Для цього спочатку обчислюємо

\[{\left(\Delta S\right)}_T=S\left(P_2,T_1\right)-S\left(P_1,T_1\right)\]

для ізотермічного оборотного перетворення з стану\(P_1\),\(T_1\) в стан, заданий\(P_2\) і\(T_1\). Для цього кроку,\(dT\) дорівнює нулю, і так

\[{\left(\Delta S\right)}_T=\int^{P_2}_{P_1}{{\left(\frac{\partial V}{\partial T}\right)}_PdP}\]

Потім ми розраховуємо

\[{\left(\Delta S\right)}_P=S\left(P_2,T_2\right)-S\left(P_2,T_1\right)\]

для ізобарного оборотного перетворення від стану\(P_2\),\(T_1\) до стану\(P_2\),\(T_2\). Для цього перетворення,\(dP\) дорівнює нулю, і

\[{\left(\Delta S\right)}_P=-\int^{T_2}_{T_1}{\frac{C_P}{T}dT}\]

Потім,

\[\Delta S^{rev}=S\left(P_2,T_2\right)-S\left(P_1,T_1\right)=\int^{T_2}_{T_1}{\frac{C_P}{T}dT}-\int^{P_2}_{P_1}{{\left(\frac{\partial V}{\partial T}\right)}_PdP}=0\]

Тому що\(\Delta S^{rev}=0\), оборотний процес унікальний; тобто\(P_1\)\(T_1\), задано\(P_2\), і, визначається кінцева температура системи. знаходимо\(T_2\) від

\[\int^{T_2}_{T_1}{\frac{C_P}{T}dT}=\int^{P_2}_{P_1}{{\left(\frac{\partial V}{\partial T}\right)}_PdP}\]

Щоб зрозуміти зміну ентропії для незворотного процесу, відзначимо спочатку, що таких процесів існує нескінченна кількість. Немає нічого унікального в кінцевій температурі. З огляду на\(P_1\)\(T_1\), і\(P_2\), кінцева температура\(T^*_2\), може мати будь-яке значення, що відповідає властивостям речовини. Щоб вказати конкретний незворотний процес, ми повинні вказати всі чотири величини\(P_1\),\(T_1\),\(P_2\), і\(T^*_2\). Зробивши це, однак, ми можемо обчислити зміну ентропії для незворотного процесу,

\[\Delta S^{irrev}=S\left(P_2,T^*_2\right)-S\left(P_1,T_1\right)>0\]

шляхом обчислення змін ентропії, оскільки ми оборотно проводимо систему вздовж ізотермічного двоступеневого шляху від\(P_1\),\(T_1\) до\(P_2\),\(T_1\) а потім вздовж ізобаричного шляху від\(P_2\),\(T_1\) до\(P_2\),\(T^*_2\). Обчислення\(\Delta S^{irrev}\) для цього оборотного шляху від\(P_1\),\(T_1\) до\(P_2\),\(T^*_2\) використовує ту ж логіку, що і розрахунок, в попередньому пункті,\(\Delta S\) для оборотного шляху від\(P_1\),\(T_1\) до\(P_2\),\(T_2\). Різниця полягає в тому, що\(T^*_2\) замінює\(T_2\) як верхню межу температурний інтеграл. Інтеграл тиску однаковий. У нас є

\[\Delta S^{irrev}=S\left(P_2,T^*_2\right)-S\left(P_1,T_1\right)=\int^{T^*_2}_{T_1}{\frac{C_P}{T}dT}-\int^{P_2}_{P_1}{{\left(\frac{\partial V}{\partial T}\right)}_PdP} >0\]

З того\(\Delta S^{irrev}>\Delta S^{rev}\), що ми маємо

\[\int^{T^*_2}_{T_1}{\frac{C_P}{T}dT}>\int^{T_2}_{T_1}{\frac{C_P}{T}dT}\]

Так як інтеграли однакові і позитивні, то випливає, що\(T^*_2>T_2\), як стверджувалося вище.

Малюнок 6. Температура проти ентропії для спонтанних і оборотних процесів.

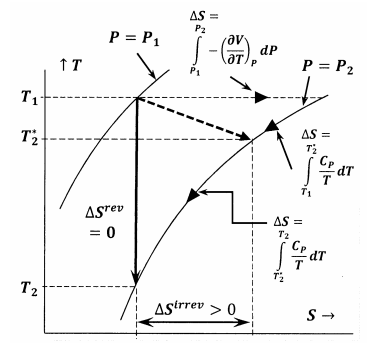
На малюнку 6 показані відносини між різними величинами, розглянутими в цьому аргументі. У першому випадку на малюнку 6 показано графік двох ізобарів системи в температурно-ентропійному просторі. Тобто лінія, позначена,\(P=P_1\) зображує набір точок температури - ентропії, в яких врівноважена система має тиск\(P_1\); лінія\(P=P_2\), позначена, зображує положення рівноваги під тиском\(P_2\). Інші лінії в цьому ескізі представляють собою шляхи, по яких система може зазнати оборотних змін при постійній ентропії або постійній температурі. Пунктирна лінія являє собою незворотний процес, при якому система переходить від стану, зазначеного\(P_1\),\(T_1\) в стан, заданий\(P_2\),\(T^*_2\). Ця лінія пунктирна, щоб уявити той факт, що температура системи може бути недостатньо чітко визначена під час незворотного процесу.

Ефективного охолодження можна домогтися за допомогою перепадів тиску, якщо система є газовою. Однак для рідин і твердих речовин\({\left({\partial V}/{\partial T}\right)}_P\) це мало; отже, зміна температури для оборотної зміни тиску також невелика. При температурах, близьких до абсолютного нуля, майже всі речовини тверді; для досягнення ефективного охолодження ми повинні змінити термодинамічну змінну, для якої температурний коефіцієнт твердої речовини є якомога більшим. Щоб розглянути загальну проблему зниження температури системи, змінюючи щось інше, ніж тиск, ми повинні розглянути систему, в якій можлива певна форма роботи без тиску - об'єму. Така система піддається додатковій силі, і її енергія змінюється в міру зміни цієї сили.

Адіабатична розмагнічування

Практичний метод, за допомогою якого досягаються надзвичайно низькі температури, називається адіабатичним розмагнічуванням. Цей метод використовує властивості парамагнітних твердих тіл. У таких твердих тілах непарні електрони, локалізовані на окремих атомах, породжують магнітний момент. Квантова механіка призводить до важливих висновків про взаємодію таких магнітних моментів і прикладеного магнітного поля: У прикладному магнітному полі квантується магнітний момент окремого атома. У найпростішому випадку він може бути вирівняний тільки в двох напрямках; він повинен бути або паралельним, або антипаралельним прикладеному магнітному полю. Коли магнітний момент атома паралельний магнітному полю, енергія системи менше, ніж коли вирівнювання є антипаралельним. Прикладений магнітне поле чинить силу на магнітні моменти, пов'язані з окремими атомами. Енергія системи залежить від величини прикладеного магнітного поля.

Замість того, щоб зосереджуватися на конкретному випадку адіабатичної розмагніченості, розглянемо енергетичні та ентропійні зміни, пов'язані зі змінами узагальненого потенціалу\({\mathit{\Phi}}_{\theta }\), та його узагальненим зміщенням\(\theta\). (Для адіабатичного розмагнічування\(\theta\) буде застосоване магнітне поле.) Для опису оборотних змін у цій системі потрібні три змінні. Ми можемо виразити енергію та ентропію як функції температури, тиску та\(\theta\):

\(E=E\left(T,P,\theta \right)\)і\(S=S\left(T,P,\theta \right)\). Сумарний диференціал ентропії включає в себе термін, який визначає залежність ентропії від\(\theta\). У нас є

\[dS={\left(\frac{\partial S}{\partial T}\right)}_{P,\theta }dT+{\left(\frac{\partial S}{\partial P}\right)}_{T,\theta }dP+{\left(\frac{\partial S}{\partial \theta }\right)}_{T,P}d\theta =\frac{C\left(T,P,\theta \right)}{T}dT-{\left(\frac{\partial V}{\partial T}\right)}_{P,\theta }dP+{\left(\frac{\partial S}{\partial \theta }\right)}_{T,P}d\theta\]

де ми пишемо,\(C\left(T,P,\theta \right)\) щоб підкреслити, що наші нинішні цілі тепер вимагають, щоб ми вимірювали теплоємність при постійному тиску і постійному\(\theta\).

Для постійного тиску, Р, і постійного зміщення\(\theta\), ентропія залежить від температури як

\[S\left(T,P,\theta \right)=S\left(0,P,\theta \right)+\int^T_0 \left(\frac{\partial S}{\partial T}\right)_{P,\theta }dT=S\left(0,P,\theta \right)+\int^T_0 \frac{C\left(T,P,\theta \right)}{T}dT\]

Постулат про те, що ентропія буде кінцевою при будь-якій температурі, передбачає, що\(\theta\) залежна від тиску і -теплоємність стає нульовою при абсолютному нулі. Тобто при абсолютному нулі теплоємність зникає незалежно від значень Р і\(\theta\). Аргумент точно такий же, як і раніше. Раніше ми писали\(C_P\left(0\right)=0\); для даного узагальненого випадку пишемо\(C\left(0,P,\theta \right)=0\).

Аналогічно з постулату про те, що ентропія йде в постійну при абсолютному нулі для всіх значень інших змінних термодинаміки, випливає, що для будь-яких двох тисків\(P_1\) і\(P_2\), і для будь-яких двох значень узагальненого зміщення,\({\theta }_1\) і\({\theta }_2\),

\[S\left(0,P_1,{\theta }_1\right)=S\left(0,P_2,{\theta }_1\right)=S\left(0,P_1,{\theta }_2\right)=S\left(0,P_2,{\theta }_2\right)=0\]

і, отже, що

\[{\left(\frac{\partial S}{\partial P}\right)}_{T=0,\theta }={\left(\frac{\partial S\left(0,P,\theta \right)}{\partial P}\right)}_{T,\theta }=0\]і\[{\left(\frac{\partial S}{\partial \theta }\right)}_{T=0,P}={\left(\frac{\partial S\left(0,P,\theta \right)}{\partial \theta }\right)}_{T,P}=0\]

Ми хочемо розглянути процес, в якому система переходить від найнижчої температури, доступної в оточенні, до ще нижчої температури. Щоб мінімізувати кінцеву температуру, цей процес необхідно проводити адіабатично. Це також повинен бути можливий процес, так що\(dS\ge 0\). Для простоти давайте тепер припустимо, що ми здійснюємо цей процес при постійному тиску\(P\), і що система переходить від стану, зазначеного\(P\)\(T_1\),,\({\theta }_1\) в стан, заданий\(P\)\(T_2\),\({\theta }_2\) де\(T_1>T_2\). Ентропіями цих двох станів є

\[S\left(T_1,P,{\theta }_1\right)=S\left(0,P,{\theta }_1\right)+\int^{T_1}_0{\frac{C\left(T,P,{\theta }_1\right)}{T}}dT\]і\[S\left(T_2,P,{\theta }_2\right)=S\left(0,P,{\theta }_2\right)+\int^{T_2}_0{\frac{C\left(T,P,{\theta }_2\right)}{T}}dT\]

Зміна ентропії для цього процесу

\[S\left(T_2,P,{\theta }_2\right)-S\left(T_1,P,{\theta }_1\right)=S\left(0,P,{\theta }_2\right)-S\left(0,P,{\theta }_1\right)\]\[+\int^{T_2}_0{\frac{C\left(T,P,{\theta }_2\right)}{T}}dT-\int^{T_1}_0{\frac{C\left(T,P,{\theta }_1\right)}{T}}dT\ge 0\]

Тепер припустимо, що кінцева температура дорівнює нулю; тобто так\(T_2=0\), щоб

\[\int^{T_2}_0{\frac{C\left(T,P,{\theta }_2\right)}{T}}dT=0\]Звідси випливає, що\[S\left(0,P,{\theta }_2\right)-S\left(0,P,{\theta }_1\right)\ge \int^{T_1}_0{\frac{C\left(T,P,{\theta }_1\right)}{T}}dT>0\]

де нерівність справа випливає з того, що\(C\left(T,P,{\theta }_1\right)>0\). Потім випливає, що

\[S\left(0,P,{\theta }_2\right)-S\left(0,P,{\theta }_1\right)>0\]

що суперечить заяві Льюїса і Рендалла третього закону. Припущення про те, що система може досягати абсолютного нуля, призводить до протиріччя заяви Льюїса і Рендалла третього закону. Тому, якщо твердження Льюїса і Рендалла вірно, абсолютний нуль недосяжний.

Зворотне також застосовується; тобто з пропозиції, що абсолютний нуль недосяжний, ми можемо показати, що твердження Льюїса та Рендалла є істинним. Для цього ми переставляємо вищевказане рівняння для\(\Delta S\),

\[\int^{T_2}_0{\frac{C\left(T,P,{\theta }_2\right)}{T}}dT\ge\]\[\int^{T_1}_0{\frac{C\left(T,P,{\theta }_1\right)}{T}}dT-S\left(0,P,{\theta }_2\right)+S\left(0,P,{\theta }_1\right)\]

Якщо тепер припустити, що заяву Льюїса і Рендалла є помилковим, вираз праворуч може бути менше або дорівнює нулю. Інтеграл зліва тоді може дорівнювати нулю, в цьому випадку система може досягати абсолютного нуля. Якщо заява Льюїса та Рендалла помилкова, це правда, що система може досягати абсолютного нуля. Тому: Якщо система не може досягти абсолютного нуля, твердження Льюїса та Рендалла вірно.

Цифри 7 і 8 зображують ці ідеї за допомогою контурних графіків у температурно-ентропійному просторі. На кожному малюнку зображені дві контурні лінії. Одна з таких контурних ліній являє собою набір значень температури і ентропії, за якими тиск постійний при\(P\) і\(\theta\) постійний при\({\theta }_1\). Інша контурна лінія являє собою сукупність значень температури і ентропії, за якими тиск постійний при\(P\) і\(\theta\) постійний при\({\theta }_2\). Ухил лінії контуру дорівнює

\[{\left(\frac{\partial T}{\partial S}\right)}_{P,\theta }=\frac{T}{C\left(T,P,\theta \right)}\]

Оскільки теплоємність завжди позитивна, цей ухил завжди позитивний.

Малюнок 7. Оборотна зміна системи, яка задовольняє твердження Льюїса та Рендалла.

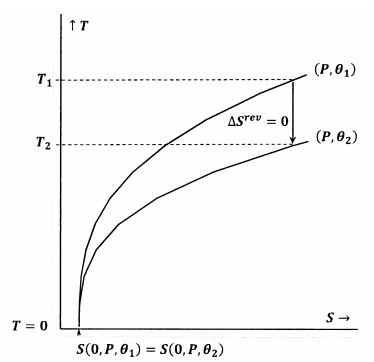
На малюнку 7 заяву Льюїса та Рендалла задовольняють. Коли температура йде до нуля, контурні лінії зустрічаються при однаковому значенні ентропії; ці контури задовольняють залежність

\[S\left(0,P,{\theta }_1\right)=S\left(0,P,{\theta }_2\right)\]

Адіабатичний (вертикальний) шлях від контуру для\(P\) і\({\theta }_1\) відповідає контуру для\(P\) і\({\theta }_2\) при плюсовій температурі,\(T_2>0\). Оскільки це, очевидно, вірно для будь-якого\(P\) і будь-якого\({\theta }_2\), остаточний стан для будь-якого адіабатичного процесу матиме\(T_2>0\). Оскільки заява Льюїса і Рендалла задоволена, система не може досягти абсолютного нуля, і навпаки.

Малюнок 8. Оборотна зміна системи, яка не задовольняє твердження Льюїса та Рендалла.

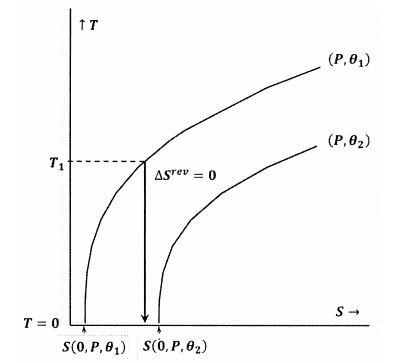
На малюнку 8 заява Льюїса і Рендалла порушується, тому що ми маємо\(S\left(0,P,{\theta }_1\right)\). При цьому адіабатичний процес, ініційований від досить низької початкової температури\(T_1\), досягне абсолютного нуля, не перетинаючи контур для постійних\(P\) і\({\theta }_2\). Оскільки заява Льюїса і Рендала порушується, система може досягати абсолютного нуля, і навпаки.