Skip to main content
LibreTexts - Ukrayinska

1.12: Восьмигранні MLSigma комплекси

  1. Last updated
  2. Save as PDF
  • Page ID
    24356

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Октаедричний комплекс містить центральний іон металу та шість кінцевих лігандів. Якщо ліганди є виключно σ-донорами, то базовий набір для лігандів визначається наступним чином,

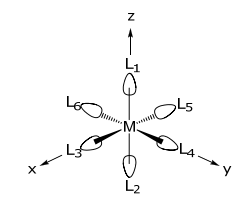
    clipboard_e21715cccc99a8c3ea6a76cc064fa59e5.png

    Ліганди, які рухаються при застосуванні операції, R, не можуть сприяти діагональному матричному елементу подання. Оскільки зв'язок σ знаходиться уздовж міжядерної осі, яка з'єднує ліганд і метал, трансформаційні властивості ліганду відповідають властивостям зв'язку M—L σ. Більше того, зв'язок σ не має зміни фази всередині міжядерної осі, отже зв'язок може трансформуватися тільки в себе (+1) або в інший ліганд (0).

    \ begin {масив} {c|cccccccccc}\ математика {O} _ {\ математика {h}} &\ математика {E} &\ математика {8C} _ {3} & 6\ математика {C} _ {2} & 6\ математика {C} _ {4} & 3\ математика {C} _ {2}\ ліворуч (=\ математика {C} _ {4} {} ^ {2}\ праворуч) &\ математика {i} & 6\ математика {~ S} _ {4} & 8\ математика {~S} _ {6} & 3\ signma_ {\ mathrm {h}} & 6\
    сигма_ {\ mathrm {d}}\\ лінія
    \ гамма_ {\ математика {L}\ сигма} & 6 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4 & 2
    \ кінець {масив}

    \[\Gamma_{\mathrm{L} \sigma}=\mathrm{a}_{1 \mathrm{~g}}+\mathrm{t}_{1 \mathrm{u}}+\mathrm{e}_{\mathrm{g}}\]

    Потрібно тепер визначити SALC базисного множини Lσ. Три різні методи доставлять SALC.

    Спосіб 1

    Як ми вже робили раніше, SALC Lσ можна визначити за допомогою оператора проекції. Зверніть увагу, що ліганд змішування в O h зберігається в чистій ротаційній підгрупі, О. може таким чином опуститися з O h → O, тим самим заощаджуючи 24 операції.

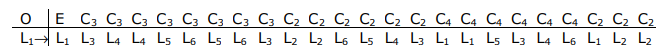
    clipboard_eb0feac3fc26cfa8abf20b1f52a8d8543.png

    Незведене зображення A 1 є абсолютно симетричним. Звідси проекція - це просто сума перерахованих вище лігандних перетворень.

    П А 1 (Л1) ~ 4 (Л1 + Л2 + Л3 + Л4 + Л5 + Л6)

    і нормалізація врожайності,

    \ (
    \ psi_ {a_ {19}} =\ frac {1} {\ sqart {6}}\ ліворуч (\ математика {~L} _ {1} +\ математика {L} _ {3} +\ математика {L} _ {4} +\ mathrm {L} _ {5} +\ mathrm m {L} _ {6}\ right)\)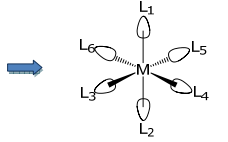clipboard_eb978a1a5361ff7aea46c100b0836e2ce.png
    Застосування оператора проекції для E нескорочуваного представлення забезпечує E g SALC.

    \ (\ почати {вирівняний}
    P^ {E}\ ліворуч (L_ {1}\ праворуч) &\ стрілка вправо\ ліворуч (2 L_ {1} -L_ {3} -L_ {4} -L_ {4} -L_ {5} -L_ {5} -L_ {5} -L_ {6} -L_ {3} +2 L_ {1} +2 L_ {2} +2 L_ {2}\ праворуч)\\
    &\ стрілка вправо\ ліворуч (4 L_ {1} +4 L_ {2} -2 L_ {3} -2 L_ {4} -2 L_ {5} -2 L_ {6}\ праворуч)
    \ кінець {вирівняний}\)

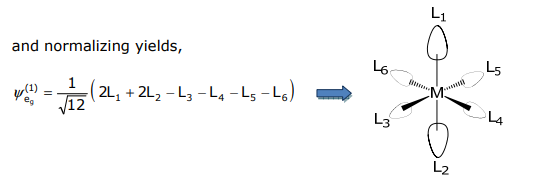
    clipboard_e308f164478f237d5d3c6fbe2d3bba629.png

    Але Е г - це подвійно вироджене представлення, а тому є ще одне SALC. Як видно зверху, оператор проекції дає лише один з двох SALC. Як ми отримуємо іншого?

    Спосіб 2

    Процедура ортогоналізації Шмідта може витягувати SALC з неортогональної лінійної комбінації відповідної основи. Припустимо, у нас є SALC, v 1, то існує v 2, який відповідає наступній умові,

    v 2 = а в 1 + у

    де u - неортогональна лінійна комбінація. Множення вищевказаного рівняння на v 1 дає,

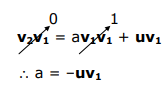
    clipboard_ee7faf8ff32de9018037815c6305f2de6.png

    Яка природа у? Розглянемо використання оператора проекції на L 3 замість L 1,

    \[\mathrm{P}^{\mathrm{e}_{9}}\left(\mathrm{~L}_{3}\right)=\frac{1}{\sqrt{12}}\left(2 \mathrm{~L}_{3}+2 \mathrm{~L}_{5}-\mathrm{L}_{1}-\mathrm{L}_{2}-\mathrm{L}_{4}-\mathrm{L}_{6}\right)\]

    Зверніть увагу, що це не дає ніякої нової інформації, тобто атомні орбіталі на одній осі вдвічі більше і поза фазою від атомних орбіталів в екваторіальній площині. Однак ця нова хвильова функція не є ψ наприклад (2), оскільки вона не ортогональна ψ наприклад (1).

    Таким чином, проекція повинна давати хвильову функцію, яка є лінійною комбінацією ψ наприклад (1) і ψ наприклад (2), тобто хвильова функція, отримана з проекції, є життєздатною u. Застосування процедури ортогоналізації Шмідта,

    \ [\ почати {вирівняний}
    a &=-\ mathbf {u v} _ {1} =-\ лівий\ ланкут\ гідророзриву {1} {\ sqrt {12}}\ лівий (2 L_ {3} +2 L_ {5} -L_ {1} -L_ {2} -L_ {4} -L_ {6}\ праворуч)\ середина\ frac {1}} {\ sqrt {12}}\ ліворуч (2 L_ {1} +2 L_ {2} -L_ {3} -L_ {4} -L_ {5} -L_ {6}\ праворуч)\ праворуч\ діапазон\\
    &=-\ frac {1} {12} [-6] =+\ frac {1} {2}
    \ кінець { вирівняні}\]

    Отже,

    \ [\ почати {вирівняний}
    \ mathbf {v} _ {2} &=\ гідророзриву {1} {2}\ гідророзриву {1} {\ sqrt {12}}\ ліворуч (2 L_ {1} +2 L_ {2} -L_ {3} -L_ {4} -L_ {5} -L_ {6}\ праворуч) +\ frac {1} {1}\ sqrt {12}}\ ліворуч (2 L_ {3} +2 L_ {5} -L_ {1} -L_ {2} -L_ {4} -L_ {6}\ право)\\
    &=\ frac {1} {\ sqrt {12}}\ ліворуч [\ frac {3} {2} L_ {3} +\ frac {3} {2} L_ {5}\ праворуч) -\ ліворуч ( \ frac {3} {2} L_ {4} +\ гідророзриву {3} {2} L_ {6}\ праворуч)\ праворуч]\ приблизно\ ліворуч (L_ {3} +L_ {5}\ праворуч) -\ ліворуч (L_ {4} +L_ {6}\ праворуч)
    \ кінець {вирівняний}\]

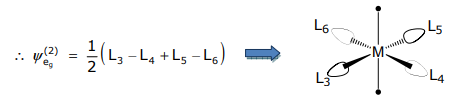
    clipboard_e9476e0a30656ba2dea4fb4c6674954cb.png

    ψ наприклад (2) ортогональний ψ наприклад (1), таким чином, це інший SALC.

    Тепер слід визначити SALC T 1g. Оператор проекції дає,

    Р Т 1 (Л 1) → (3Л 1-Л 2-Л 2-Л 6-Л 5-Л 4-Л 3-Л 1 + Л 1 + Л 5 + Л 3 + Л 3 + Л 4 + Л 6-Л 1 — Л (1 — Л 2)

    П Т 1 (Л 1) ~ 3 (Л 1 — Л 2)

    і нормалізація врожайності,

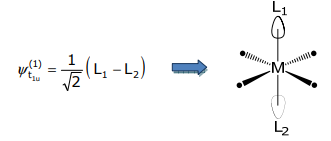
    clipboard_e3e08541cf2ac8b59819acfab2bc1df8e.png

    Застосовуючи метод ортогоналізації Шмідта,

    $
    \ mathrm {P} ^ {\ mathrm {T} _ {1}}\ ліворуч (\ mathrm {~L} _ {3}\ праворуч)\ sim 3\ ліворуч (\ mathrm {~L} _ {L} _ {5}\ праворуч)\ стрілка вправо\ psi_ {\ mathrm {t} _ {\ mathrm} _ {\ mathrm m {lu}} =\ frac {1} {\ sqrt {2}}\ ліворуч (\ математика {~L} _ {3} -\ математика {L} _ {5}\ справа)
    \]

    Ця хвильова функція ортогональна ψ t 1u (1), отже, це, ймовірно, SALC. Може довести це, застосувавши процес ортогоналізації Шмідта t1u і встановивши це бути u. рішення для,

    $
    \ почати {
    вирівняний} а &=-\ mathbf {u}\ mathbf {v} _ {1} =-\ лівий\ кут\ frac {1} {\ sqrt {2}}\ лівий (\ mathrm {~L} _ {2}\ правий)\ mathrm {1} {1} -\ mathrm {L} _ {2}\ праворуч)\ середина\ frac {1} {\ sqrt {2}}\ ліворуч (\ mathrm {~L} _ {3} -\ mathrm {L} _ {5}\ праворуч)\ праворуч\ діапазон\\
    &=-\ frac {1} {2} (0) =0
    \ кінець {вирівняний}
    \]

    і

    $
    v_ {2} =a v_ {1} +u=0\ cdot\ frac {1} {\ sqrt {2}}\ ліворуч (L_ {1} -L_ {2}\ праворуч) +\ frac {1} {\ sqrt {2}}\ ліворуч (L_ {3} -L_ {5}\ праворуч)
    \]

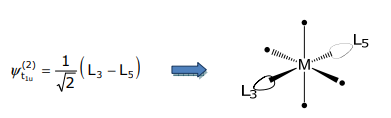
    clipboard_e579af70e4a8bcb24d8a0c0773b6c9eb2.png

    Отже, як підозрюється, це SALC. І третій SALC T 1u симетрії є (L 4, L 6) пара.

    clipboard_e7b9d3496d928a71ab7e89ac538f94213.png

    Спосіб 3

    Для тих САЛК з симетріями, які такі ж, як s, p або d орбіталі, можуть адаптувати симетрію ліганду, встановленого до симетрії металевих орбіталей.

    Розглянемо орбітальну dz2, яка більш точно визначається як 2z 2 — x 2 — y 2. Таким чином, коефіцієнт осі z вдвічі більше, ніж x і y і поза фазою з x і y. ліганди на осі z, L 1 і L 2, тому повинні бути вдвічі більше і протилежного знаку екваторіальних лігандів, L 3, L 4, L 5, L 6. Це призводить природно до того,

    $
    \ почати {вирівняний}
    &\ psi_ {\ mathrm {e} _ {9}} ^ {(1)}\ приблизно 2\ математика {~L} _ {1} +2\ mathrm {L} _ {2} -\ математика {L} _ {3} -\ математика {L} _ {4} -\ математика {L} _ {5} -\ математика {L} _ {6}\\
    &\ psi_ {\ mathrm {e} _ {9}} ^ {(1)} =\ frac {1} {\ sqrt {12}}\ ліворуч (2\ матрм {~L} _ {2}} -\ математика {L} _ {3} -\ математика {L} _ {4} -\ математика {L} _ {5} -\ математика {L} _ {6}\ праворуч)
    \ кінець {вирівняний}
    \]

    Інший SALC цього виродженого множини задається d x 2 —y 2, який не має коефіцієнта на z, та коефіцієнти x та y, які рівні, але протилежного знаку. Шляхом симетрії відповідності орбітальної,

    $
    \ почати {вирівняний}
    &\ psi_ {\ mathrm {e} _ {9}} ^ {(2)}\ приблизно\ математика {L} _ {3} -\ математика {L} _ {4} +\ математика {L} _ {5} -\ математика {L} _ {6} _\
    &\ psi_ {\ mathrm {e} {9}} ^ {(2)} =\ frac {1} {2}\ ліворуч (\ математика {~L} _ {3} -\ математика {L} _ {4} +\ mathrm {L} _ {5} -\ mathrm {L} _ {6}\ праворуч)
    \ кінець {вирівняний}}
    \]

    Інші SALC слідують цьому прикладу.

    t 2g d-орбітальний набір (тобто d xy, d xz, d yz) має неправильну симетрію для взаємодії з безліччю лігандів Lσ і, таким чином, не зв'язується. Це видно з орбітальної картини. Lσ орбіталі спрямовані між частками t 2g d-орбіталей,

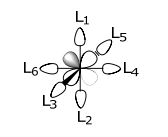
    clipboard_e2bc139426dd3d11cf70dea3a43e8fd1b.png

    Перекриватися можуть тільки металеві орбіталі і САЛК однакової симетрії. У разі восьмигранного МЛ 6 σ -комплексу,

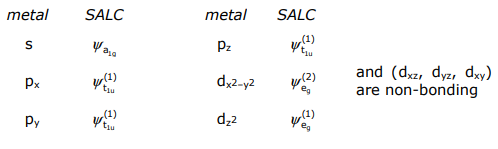
    clipboard_ebef81f886508965407f6bb85e686f1ca.png

    З огляду на вищезазначені міркування ΔE ML та S ML, діаграма МО для M (Lσ) 6 побудована з Co (NH 3) 6 3+ як приклад,

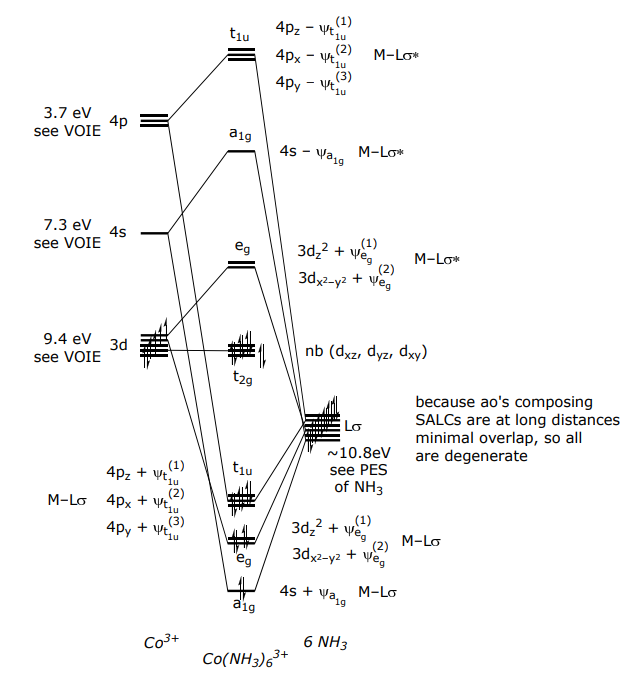
    clipboard_eae2a3b97d25d366278eef5461c4ae4cd.png

    Енергії взаємодії ε σ і ε σ * (тобто недіагональних елементів матриці, H ML) менше різниці енергій металу і лігандів атомних орбіталей (тобто діагональних елементів матриці, H MM і H LL), тому молекулярна орбіталі залишаються в межах своїх енергетичних «зон».