4.3.2: Представлення груп точок
- Page ID
- 33601
Операції симетрії: матричні зображення
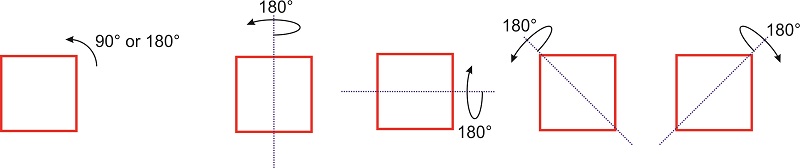
Операція симетрії, така як обертання навколо осі симетрії або відображення через площину, - це операція, яка при виконанні над об'єктом призводить до нової орієнтації об'єкта, яка не відрізняється від оригіналу. Наприклад, якщо ми обертаємо квадрат у площині за\(\pi/2\) або\(\pi\), нова орієнтація квадрата накладається на вихідну (рис.\(\PageIndex{1}\)).
Якщо обертання на кут\(\theta\) молекули (або об'єкта) навколо якоїсь осі призводить до орієнтації молекули (або об'єкта), яка накладається на оригінал, вісь називається віссю обертання. Молекула (або об'єкт), як кажуть, має вісь обертання\(n\) -fold, де\(n\) є\(2\pi/\theta\). Вісь позначається як\(C_n\). Квадрат фігури\(\PageIndex{1}\) має\(C_4\) вісь, перпендикулярну площині, оскільки\(90^{\circ}\) обертання залишає фігуру невідмінною від початкової орієнтації. Ця вісь також є\(C_2\) віссю, оскільки\(180^{\circ}\) градусний поворот залишає квадрат невідмінним від початкового квадрата. Крім того, фігура має кілька інших\(C_2\) осі, які лежать на тій же площині, що і квадрат:
Операція симетрії переміщує всі точки об'єкта з однієї початкової позиції в кінцеву позицію, а це означає, що оператори симетрії є\(3\times 3\) квадратними матрицями (або\(2\times 2\) у двох вимірах). Кожна операція симетрії може бути виражена у вигляді матриці перетворення, де вектор\((x',y',z')\) представляє нові координати точки\((x,y,z)\) після операції симетрії.
\[[\text{New Coordinates} (x',y',z')] = [\text{Transformation Matrix}] \times [\text{Old Coordinates} (x,y,z)] \nonumber \]
Ми будемо використовувати приклад води, яка знаходиться в\(C_{2v}\) точковій групі, щоб проілюструвати, як матриці перетворення можуть бути використані для представлення симетрії групи.
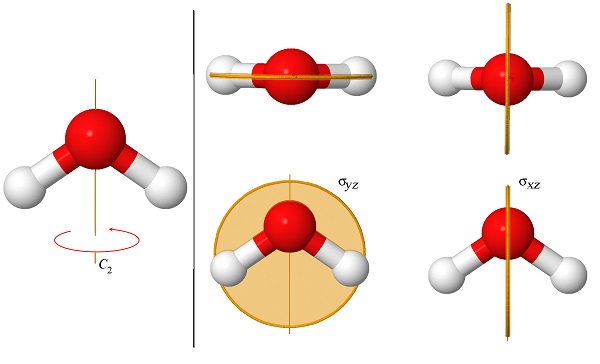
\(\PageIndex{2}\)На малюнку показані три елементи симетрії молекули води (H\(_2\) O). Ця молекула має тільки одну вісь обертання, яка в 2 рази, і тому ми називаємо її «\(C_2\)віссю». Він також має дві дзеркальні площини, одна з яких містить два атоми водню (\(\sigma_{yz}\)), а інша перпендикулярна їй (\(\sigma_{xz}\)). Обидві площини містять\(_2\) вісь С.
Матриця перетворення\(C_2\) обертання
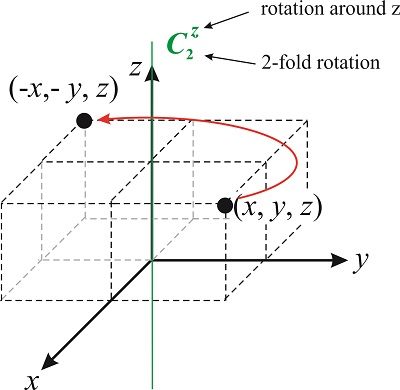
Двократне обертання навколо\(z-\) осі змінює розташування точки\((x,y,z)\) на\((-x,-y,z)\) (див. Рис.\(\PageIndex{3}\)). За умовністю обертання завжди приймаються в напрямку проти годинникової стрілки.
Що таке матриця, яка представляє\(C_2\) обертання? Матриця перетворює вектор\((x,y,z)\) в\((-x,-y,z)\), так
\[{C_2}(x,y,z)=(-x,-y,z) \nonumber \]
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} -x \\ -y \\ z \end{pmatrix} \nonumber \]
Ми знаємо, що матриця є\(3\times 3\) квадратною матрицею, тому що їй потрібно помножити тривимірний вектор. Крім того, ми запишемо вектор у вигляді вертикального стовпця, щоб задовольнити вимоги множення матриці.
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix} \nonumber \]
\[a_{11}x+a_{12}y+a_{13}z=-x \nonumber \]
\[a_{21}x+a_{22}y+a_{23}z=-y \nonumber \]
\[a_{31}x+a_{32}y+a_{33}z=z \nonumber \]
і робимо висновок\(a_{11}=-1\), що,\(a_{12}=a_{13}=0\),\(a_{22}=-1\),\(a_{21}=a_{23}=0\) і\(a_{33}=1\),\(a_{31}=a_{32}=0\). Матриця трансформації\(C_2\) операції групи\(C_{2v}\) точок становить:
\[C_2=\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]
Матриця трансформації\(\sigma_{xz}\) відображення
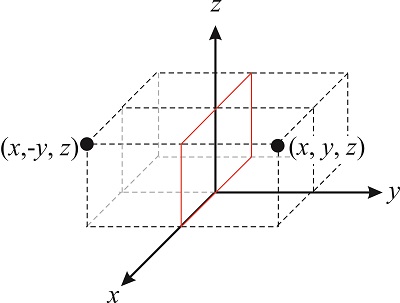
Обертання - це не єдині операції симетрії, які ми можемо виконувати над молекулою. Малюнок\(\PageIndex{4}\) ілюструє відображення точки через\(xz\) площину. Ця операція перетворює вектор\((x,y,z)\) в вектор\((x,-y,z)\). Оператори симетрії, що включають відображення через площину, зазвичай позначаються буквою\(\sigma\), тому оператор, який відображає точку через\(xz\) площину, такий\(\hat{\sigma}_{xz}\):
\[\sigma_{xz}(x,y,z)=(x,-y,z) \nonumber \]
За тією ж логікою, яку ми використовували для матриці обертання, ми можемо записати матрицю\(\sigma_{xz}\) перетворення як:
\[\sigma_{x,z}=\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]
Це правда, тому що
\[\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} x \\ -y \\ z \end{pmatrix} \nonumber \]
Знайдіть матрицю перетворення ідентичності (E) та\(\sigma_{y,z}\) операції під групою\(C_{2v}\) точок.
- Відповідь
-
Матриця перетворення для\(E\) is\(\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\).
Матриця перетворення для\(\sigma_{v(yz)"}\) is\(\begin{pmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\).
Персонажі
Для квадратної матриці символом є слід матриці. Для\(C_2\) операції, з матрицею перетворення
\[\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}, \nonumber \]
слід є\((-1) + (-1) + 1 = -1\).
Набір символів для групи точок називається скорочуваним представленням (\(\Gamma\)). Скорочуване подання для групи\(C_{2v}\) точок:
\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]
Доведіть, що символи в зведеному поданні для\(C_{2v}\) є правильними:
\[\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]
- Відповідь
-
Для\(E\) операції з матрицею\(\begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\) перетворення слід\(1 + 1 + 1 = \)\(3\).
Для\(C^z_2\) операції з матрицею\(\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\) перетворення слід\((-1) + (-1) + 1 =\)\( -1\).
Для\(\sigma_{v(xz)'}\) операції з матрицею\(\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber\) перетворення слід\(1 + (-1) + 1 =\)\(1\).
Для\(\sigma_{v(yz)"}\) операції з матрицею\(\begin{pmatrix} -1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} \nonumber\) перетворення слід\(-1 + 1 + 1 =\)\(1\).
Це дає зведене уявлення\(\begin{array}{l|llll} C_{2v} & E & C_2 & \sigma_v & \sigma_v' \\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \)
Зводні та нескоротні уявлення
Давайте тепер повернемося назад і більш детально розглянемо матриці перетворення\(C_{2v}\) point group that we derived above. If we look at the matrices carefully we see that they all take the same block diagonal form (a square matrix is said to be block diagonal if all the elements are zero except for a set of submatrices lying along the diagonal).
\[E=\begin{pmatrix} {\color{red}[1]}&0&0 \\ 0&{\color{blue}[1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix}, \, C_2=\begin{pmatrix} {\color{red}[-1]}&0&0 \\ 0&{\color{blue}[-1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} ,\, \sigma_{v(xz)}'=\begin{pmatrix} {\color{red}[1]}&0&0 \\ 0&{\color{blue}[-1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} ,\, \sigma_{v(yz)"}=\begin{pmatrix} \color{red}[-1]&0&0 \\ 0&{\color{blue}[1]}&0 \\ 0&0&{\color{green}[1]} \end{pmatrix} \nonumber \]
Всі ненульові елементи стають матрицями 1x1, кожен з яких представляє окремі\({\color{red}x}, {\color{blue}y}, {\color{green}z}\) координати. Іншими словами, елемент\(\color{red}a_{11}\) представляє\(\color{red}x\)\(\color{blue}y\),\(\color{blue}a_{22}\) представляє і\(\color{green}a_{33}\) представляє\(\color{green}z\). Елементи матриці для x з кожної матриці перетворення об'єднуються, утворюючи незведене уявлення\(C_{2v}\) точкової групи. Аналогічно, елементи матриці для y об'єднуються, щоб утворити друге незведене уявлення, і те саме вірно для z елементів. Ці нескоротні уявлення наведені нижче:
\[\begin{array}{l|llll|l} C_{2v} & E & C_2 & \sigma_v & \sigma_v' & \text{Coordinate Used}\\ \hline & \color{red}1 & \color{red}-1&\color{red}1&\color{red}-1 & \color{red}x \\ & \color{blue}1 & \color{blue}-1 & \color{blue}-1 & \color{blue}1 & \color{blue}y \\ & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}1 & \color{green}z\\ \hline \Gamma & 3 & -1 & 1 & 1 \end{array} \nonumber \]
Незведені уявлення додають до формування зведеного представлення,\(\Gamma\). Це\(\Gamma\), яке є набором матриць 3х3, можна звести до безлічі матриць 1х1 нескорочуваних уявлень. Незведені уявлення не можуть бути зменшені далі, звідси і їх назва.
Джерела та атрибуція
- Parts of this page was adapted from Matrices (click here) (Symmetry Operators), contributed by Marcia Levitus, Associate Professor (Biodesign Institute) at Arizona State University.
- Parts of this page were adapted from Reductions of Representations, contributed by Template:ContribVallance
- Template:ContribHaas