4.3.1: Матриці
- Page ID
- 33602
Симетрія молекул має важливе значення для розуміння структур і властивостей органічних і неорганічних сполук. Властивості хімічних сполук часто легко пояснюються розглядом симетрії. Наприклад, симетрія молекули визначає, чи має молекула постійний дипольний момент чи ні. Теорії, що описують оптичну активність, інфрачервону та ультрафіолетову спектроскопію та кристалічну структуру, передбачають застосування міркувань симетрії. Матрична алгебра є найважливішим математичним інструментом в описі симетрії.
Властивості груп симетрії організовані в символьних таблицях (розглянуто далі в цьому розділі). Таблиці символів будуються на основі матриць. На цій сторінці наведено короткий опис матриць і множення матриць.
Що таке матриця?
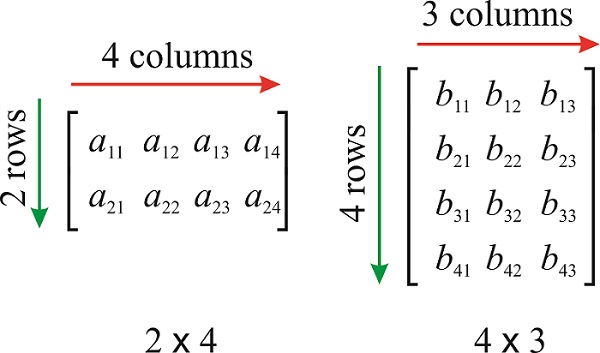
\(m\times n\)Матриця\(\mathbf{A}\) являє собою прямокутний масив чисел з\(m\) рядками і\(n\) стовпцями. Цифри\(m\) і\(n\) є розмірами\(\mathbf{A}\). Числа в матриці називаються її записами. \(j\)Викликається запис у рядку\(i\) та стовпці\(a_{ij}\).
Деякі типи матриць мають особливі назви:
- Квадратна матриця:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix} \nonumber \] з\(m=n\)
- Прямокутна матриця:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\nonumber \] з\(m\neq n\)
- Вектор стовпця:\[\begin{pmatrix} 3 \\ 5\\ -i \end{pmatrix}\nonumber \] з\(n=1\)
- Вектор рядка:\[\begin{pmatrix} 3 &-2 &4 \\ \end{pmatrix}\nonumber \] з\(m=1\)
- Матриця ідентичності:\[\begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0&0 &1 \end{pmatrix}\nonumber \] with\(a_{ij}=\delta_{i,j}\), де\(\delta_{i,j}\) - функція, визначена як\(\delta_{i,j}=1\) if\(i=j\) і\(\delta_{i,j}=0\) if\(i\neq j\).
- Діагональна матриця:\[\begin{pmatrix} a &0 &0 \\ 0 &b &0 \\ 0&0 &c \end{pmatrix}\nonumber \] с\(a_{ij}=c_i \delta_{i,j}\).
- Верхня трикутна матриця:\[\begin{pmatrix} a &b &c \\ 0 &d &e \\ 0&0 &f \end{pmatrix}\nonumber \] Усі записи під основною діагоналлю дорівнюють нулю.
- Нижня трикутна матриця:\[\begin{pmatrix} a &0 &0 \\ b &c &0 \\ d&e &f \end{pmatrix}\nonumber \] Усі записи над основною діагоналлю дорівнюють нулю.
- Трикутна матриця - це та, яка є або нижньою трикутною, або верхньою трикутною.
Слід матриці
Слід\(n\times n\) квадратної матриці\(\mathbf{A}\) - це сума діагональних елементів, і формально визначена як\(Tr( \mathbf{A})=\sum_{i=1}^{n}a_{ii}\).
Наприклад,
\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix}\; ; Tr(\mathbf{A})=12+3i \nonumber \]
Сингулярні та несингулярні матриці
Квадратна матриця з ненульовим детермінантом називається несингулярною. Матриця, детермінант якої дорівнює нулю, називається одниною. (Зауважте, що ви не можете обчислити детермінант неквадратної матриці).
Для матриці 2х2
\[\mathbf{B}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\; ; det(\mathbf{B})= ad - cb \nonumber \]
Для матриці 3х3
\[\mathbf{C}=\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \nonumber \]
\[det(\mathbf{C})=a\begin{pmatrix} e & f \\ h & i \end{pmatrix} - b\begin{pmatrix} d & f \\ g & i \end{pmatrix} + c\begin{pmatrix} d & e \\ g & h \end{pmatrix} \nonumber \]
\[det(\mathbf{C})= aei - ahf -bdi + bgf + cdh - cge \nonumber \]
Транспонування матриці
Транспонування матриці, найчастіше записане\(\mathbf{A}^T\), - це матриця, отримана шляхом обміну\(\mathbf{A}\) рядками та стовпцями. Його отримують шляхом заміни всіх елементів\(a_{ij}\) на\(a_{ji}\). Наприклад:
\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\rightarrow \mathbf{A}^T=\begin{pmatrix} 3 &5\\ -2 &3i\\ 4&3 \end{pmatrix} \nonumber \]
Множення матриць
Для множення двох матриць кількість вертикальних стовпців в першій матриці має бути таким же, як і кількість рядків у другій матриці. Якщо\(\mathbf{A}\) має розміри\(m\times n\) і\(\mathbf{B}\) має розміри\(n\times p\),\(\mathbf{AB}\) то виріб визначено, і має розміри\(m\times p\).
\[c_{ij} = \sum a_{ij} \times b_{ij} \nonumber \]
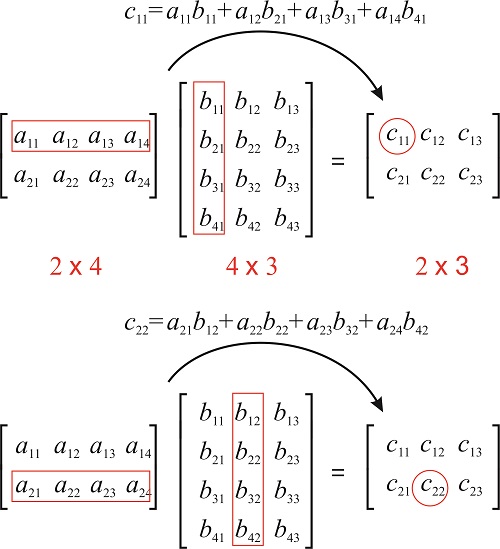
Запис\(a_{ij} \times b_{ij}\) отримується\(i\) множенням рядка\(\mathbf{A}\) на стовпець\(j\)\(\mathbf{B}\), що робиться шляхом множення відповідних записів разом з подальшим додаванням результатів:
Розрахувати товар
\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1 &0 \\ 5 &3 \\ -1 &0 \end{pmatrix} \nonumber \]
Рішення
Нам потрібно помножити\(3\times 3\) матрицю на\(3\times 2\) матрицю, тому ми очікуємо\(3\times 2\) матрицю в результаті.
\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1 &0 \\ 5 &3 \\ -1 &0 \end{pmatrix}=\begin{pmatrix} a&b \\ c&d \\ e &f \end{pmatrix} \nonumber \]
Для обчислення\(a\), який є запис (1,1), використовуємо рядок 1 матриці зліва і стовпець 1 матриці праворуч:
\[\begin{pmatrix} {\color{red}1} &{\color{red}-2} &{\color{red}4} \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} {\color{red}1} &0 \\ {\color{red}5} &3 \\ {\color{red}-1} &0 \end{pmatrix}=\begin{pmatrix} {\color{red}a}&b \\ c&d \\ e &f \end{pmatrix}\rightarrow a=1\times 1+(-2)\times 5+4\times (-1)=-13 \nonumber \]
Для обчислення\(b\), який є запис (1,2), використовуємо рядок 1 матриці зліва і стовпець 2 матриці праворуч:
\[\begin{pmatrix} {\color{red}1} &{\color{red}-2} &{\color{red}4} \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1&{\color{red}0} \\ 5&{\color{red}3} \\ -1&{\color{red}0} \end{pmatrix}=\begin{pmatrix} a&{\color{red}b} \\ c&d \\ e &f \end{pmatrix}\rightarrow b=1\times 0+(-2)\times 3+4\times 0=-6 \nonumber \]
Для обчислення\(c\), який є запис (2,1), використовуємо рядок 2 матриці зліва і стовпець 1 матриці праворуч:
\[\begin{pmatrix} 1&-2&4\\ {\color{red}5} &{\color{red}0} &{\color{red}3} \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} {\color{red}1} &0 \\ {\color{red}5} &3 \\ {\color{red}-1} &0 \end{pmatrix}=\begin{pmatrix} a&b \\ {\color{red}c}&d \\ e &f \end{pmatrix}\rightarrow c=5\times 1+0\times 5+3\times (-1)=2 \nonumber \]
Для обчислення\(d\), який є запис (2,2), використовуємо рядок 2 матриці зліва і стовпець 2 матриці праворуч:
\[\begin{pmatrix} 1&-2&4\\ {\color{red}5} &{\color{red}0} &{\color{red}3} \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1&{\color{red}0} \\ 5&{\color{red}3} \\ -1&{\color{red}0} \end{pmatrix}=\begin{pmatrix} a&b \\ c&{\color{red}d} \\ e &f \end{pmatrix}\rightarrow d=5\times 0+0\times 3+3\times 0=0 \nonumber \]
Для обчислення\(e\), який є запис (3,1), використовуємо рядок 3 матриці зліва і стовпець 1 матриці праворуч:
\[\begin{pmatrix} 1&-2&4\\ 5&0&3 \\ {\color{red}0} &{\color{red}1/2} &{\color{red}9} \end{pmatrix}\begin{pmatrix} {\color{red}1} &0 \\ {\color{red}5} &3 \\ {\color{red}-1} &0 \end{pmatrix}=\begin{pmatrix} a&b \\ c&d \\ {\color{red}e} &f \end{pmatrix}\rightarrow e=0\times 1+1/2\times 5+9\times (-1)=-13/2 \nonumber \]
Для обчислення\(f\), яка є запис (3,2), використовуємо рядок 3 матриці зліва і стовпець 2 матриці праворуч:
\[\begin{pmatrix} 1&-2&4\\ 5&0&3 \\ {\color{red}0} &{\color{red}1/2} &{\color{red}9} \end{pmatrix}\begin{pmatrix} 1&{\color{red}0} \\ 5&{\color{red}3} \\ -1&{\color{red}0} \end{pmatrix}=\begin{pmatrix} a&b \\ c&d \\ e&{\color{red}f} \end{pmatrix}\rightarrow f=0\times 0+1/2\times 3+9\times 0=3/2 \nonumber \]
В результаті виходить:
\[\displaystyle{\color{Maroon}\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ 0 & 1/2 &9 \end{pmatrix}\begin{pmatrix} 1 &0 \\ 5 &3 \\ -1 &0 \end{pmatrix}=\begin{pmatrix} -13&-6 \\ 2&0 \\ -13/2 &3/2 \end{pmatrix}} \nonumber \]
Обчисліть
\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}\nonumber \]
Рішення
Нас просять помножити\(2\times 3\) матрицю на\(3\times 1\) матрицю (вектор стовпця). Результатом буде\(2\times 1\) матриця (вектор).
\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}=\begin{pmatrix} a \\ b \end{pmatrix}\nonumber \]
\[a=1\times1+(-2)\times 5+ 4\times (-1)=-13\nonumber \]
\[b=5\times1+0\times 5+ 3\times (-1)=2\nonumber \]
Рішення полягає в:
\[\displaystyle{\color{Maroon}\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}=\begin{pmatrix} -13 \\ 2 \end{pmatrix}}\nonumber \]
Потрібна допомога? Посилання нижче містить розв'язані приклади: Множення матриць різної форми (три приклади): http://tinyurl.com/kn8ysqq
Зовнішні посилання:
- Множення матриць, приклад 1: http://patrickjmt.com/matrices-multiplying-a-matrix-by-another-matrix/
- Множення матриць, приклад 2: http://patrickjmt.com/multiplying-matrices-example-2/
- Множення матриць, приклад 3: http://patrickjmt.com/multiplying-matrices-example-3/
Комутатор
Матричне множення не є, в загальному, комутативним. Наприклад, ми можемо виконати
\[\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix}\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}=\begin{pmatrix} -13 \\ 2 \end{pmatrix} \nonumber \]
але не може виконувати
\[\begin{pmatrix} 1 \\ 5 \\ -1 \end{pmatrix}\begin{pmatrix} 1 &-2 &4 \\ 5 &0 &3 \\ \end{pmatrix} \nonumber \]
Навіть з квадратними матрицями, які можна множити обома способами, множення не є комутативним. У цьому випадку корисно визначити комутатор, який визначається як:
\[[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A} \nonumber \]
Дано\(\mathbf{A}=\begin{pmatrix} 3&1 \\ 2&0 \end{pmatrix}\) і\(\mathbf{B}=\begin{pmatrix} 1&0 \\ -1&2 \end{pmatrix}\)
Обчисліть комутатор\([\mathbf{A},\mathbf{B}]\)
Рішення
\[[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A}\nonumber \]
\[\mathbf{A}\mathbf{B}=\begin{pmatrix} 3&1 \\ 2&0 \end{pmatrix}\begin{pmatrix} 1&0 \\ -1&2 \end{pmatrix}=\begin{pmatrix} 3\times 1+1\times (-1)&3\times 0 +1\times 2 \\ 2\times 1+0\times (-1)&2\times 0+ 0\times 2 \end{pmatrix}=\begin{pmatrix} 2&2 \\ 2&0 \end{pmatrix}\nonumber \]
\[\mathbf{B}\mathbf{A}=\begin{pmatrix} 1&0 \\ -1&2 \end{pmatrix}\begin{pmatrix} 3&1 \\ 2&0 \end{pmatrix}=\begin{pmatrix} 1\times 3+0\times 2&1\times 1 +0\times 0 \\ -1\times 3+2\times 2&-1\times 1+2\times 0 \end{pmatrix}=\begin{pmatrix} 3&1 \\ 1&-1 \end{pmatrix}\nonumber \]
\[[\mathbf{A},\mathbf{B}]=\mathbf{A}\mathbf{B}-\mathbf{B}\mathbf{A}=\begin{pmatrix} 2&2 \\ 2&0 \end{pmatrix}-\begin{pmatrix} 3&1 \\ 1&-1 \end{pmatrix}=\begin{pmatrix} -1&1 \\ 1&1 \end{pmatrix}\nonumber \]
\[\displaystyle{\color{Maroon}[\mathbf{A},\mathbf{B}]=\begin{pmatrix} -1&1 \\ 1&1 \end{pmatrix}}\nonumber \]
Множення вектора на скаляр
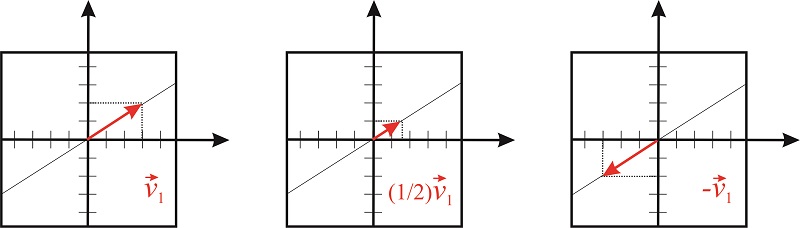
Множення вектора\(\vec{v_1}\) на скаляр\(n\) дає інший вектор тих же розмірів, який лежить в тому ж напрямку, що і\(\vec{v_1}\);
\[n\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} nx \\ ny \end{pmatrix} \nonumber \]
Скаляр може розтягувати або стискати довжину вектора, але не може обертати його (рисунок [рис:vector_by_scalar]).
Множення квадратної матриці на вектор
Множення вектора\(\vec{v_1}\) на квадратну матрицю дає інший вектор таких же розмірів\(\vec{v_1}\). Наприклад, ми можемо помножити\(2\times 2\) матрицю і двовимірний вектор:
\[\begin{pmatrix} a&b \\ c&d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} ax+by \\ cx+dy \end{pmatrix} \nonumber \]
Для прикладу розглянемо матрицю
\[\mathbf{A}=\begin{pmatrix} -2 &0 \\ 0 &1 \end{pmatrix} \nonumber \]
Виріб
\[\begin{pmatrix} -2&0 \\ 0&1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \nonumber \]
є
\[\begin{pmatrix} -2x \\ y \end{pmatrix} \nonumber \]
Ми бачимо, що\(2\times 2\) матриці діють як оператори, які перетворюють один двовимірний вектор в інший двовимірний вектор. Саме ця матриця зберігає значення\(y\) постійної і множить значення\(x\) на -2 (рис.\(\PageIndex{3}\)).
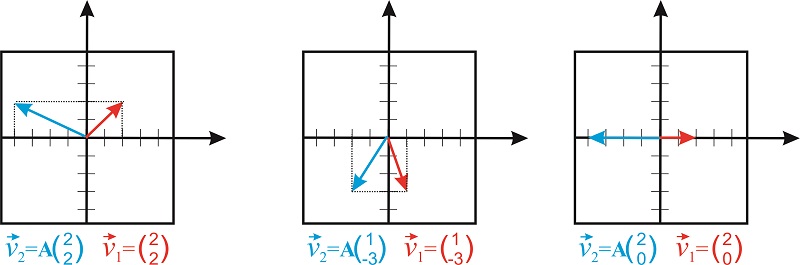
Зверніть увагу, що матриці є корисними способами представлення операторів, які змінюють орієнтацію та розмір вектора. Важливим класом операторів, що представляють особливий інтерес для хіміків, є так звані оператори симетрії.
Атрибуція
Ця сторінка була адаптована з матриць (натисніть тут), яку внесла Марсія Левітус, доцент (Інститут біодизайну) в Університеті штату Арізона.