4.3: Властивості та представлення груп

Last updated
Save as PDF

Page ID: 33598

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Натисніть тут, щоб побачити лекцію на цю тему.

Групове множення

Тепер ми дослідимо, що відбувається, коли ми застосовуємо дві операції симетрії послідовно. Як приклад розглянемо\(NH_3\) молекулу, яка відноситься до\(C_{3v}\) точкової групи. Розглянемо, що станеться, якщо застосувати\(C_3\) обертання (120˚ проти годинникової стрілки) з подальшим \(\sigma_v\)відображенням (відображенням над \(\sigma_v\)віссю). Ми пишемо цю комбіновану операцію \(\sigma_v\)\(C_3\)(коли написано, операції симетрії оперують річчю безпосередньо праворуч, так само, як це роблять оператори в квантовій механіці - тому нам доводиться працювати назад справа наліво від позначення, щоб отримати правильний порядок, в якому застосовуються оператори). Як ми незабаром побачимо, порядок, в якому застосовуються операції, важливий.

альт

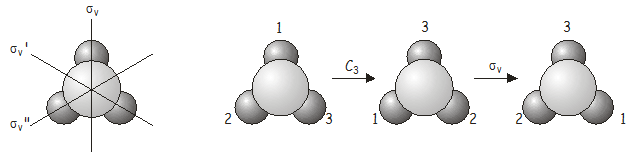
\(\sigma_v\)\(C_3\)Комбінована операція еквівалентна \(\sigma_v''\)(зверніть увагу на подвійне\(\sigma_v''\) просте!) , Що також є операцією симетрії\(C_{3v}\) точкової групи. Тепер подивимося, що буде, якщо застосувати оператори в зворотному порядку, тобто,\(C_3\)\(\sigma_v\) is (\(\sigma_v\)слідом \(C_3\)).

альт

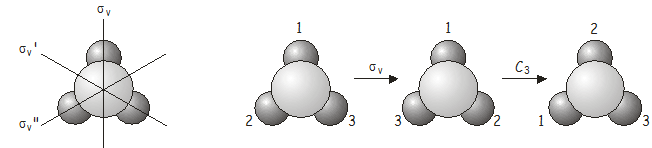
Знову ж таки,\(C_3\)\(\sigma_v\) комбінована операція еквівалентна іншій операції групи точок, цього разу \(\sigma_v'\)(зверніть увагу на єдиний простий\(\sigma_v'\)!) .

Є два важливих моменти, які ілюструються цим прикладом:

Важливий порядок, в якому застосовуються дві операції. Для двох операцій симетрії\(A\) і\(B\),\(AB\) не обов'язково те ж саме\(BA\), що, тобто операції симетрії взагалі не коммутують. У деяких групах елементи симетрії їздять на роботу; такі групи, як кажуть, є абелівськими.
Якщо послідовно застосовувати дві операції з однієї групи точок, результат буде еквівалентний іншій операції з групи точок. Операції симетрії, які пов'язані один з одним іншими операціями симетрії групи, належать до одного класу. У\(NH_3\), три дзеркальні площини \(\sigma_v\), \(\sigma_v'\)і \(\sigma_v''\)належать до одного класу (пов'язані один з одним за допомогою\(C_3\) обертання), як\(C_3^+\) і обертання і\(C_3^-\) (проти годинникової стрілки і обертання за годинниковою стрілкою навколо головного осі, пов'язані один з одним вертикальною дзеркальною площиною).

Чотири властивості математичних груп

Тепер, коли ми вивчили деякі властивості операцій і елементів симетрії та їх поведінку в точкових групах, ми готові ввести формальне математичне визначення групи. Наведені нижче визначення будуть введені в контекст молекулярної симетрії.

Математична група визначається як сукупність елементів (\(A_1\),\(A_2\),\(A_3\)...) разом з правилом формування комбінацій\(A_i\),\(A_j\)... Для наших цілей,\(A_1\)\(A_2\)\(A_3\), і т.д. є елементами симетрії і\(A_i\)\(A_j\), і т.д. є операціями симетрії, описаними в попередньому розділі. Елементи групи і правило їх об'єднання повинні задовольняти наступним чотирьом критеріям.

Група повинна включати в себе особистість\(E\), яка їздить з іншими членами групи. Іншими словами, \(E A_i= A_i \)для всіх елементів групи. Застосування операції ідентифікації до або після іншої операції, призводить до того ж результату\(A_i\), що і\(A_i\) поодинці.
Елементи повинні задовольняти властивість групи, що поєднання будь-якої пари елементів також є елементом групи. Наприклад, у\(C_{3v}\) точковій групі обертання C ₃, за яким слідує a,\(\sigma_v\) дає іншу операцію, яка вже є частиною групи: a\(\sigma_v"\).
Кожна операція симетрії\(A_i\) повинна мати зворотний\(A_i^{-1}\), який також є елементом групи, таким чином, що\[A_i A_i^{-1} = A_i^{-1}A_i = E \nonumber \] зворотний\(g_i^{-1}\) ефективно «скасовує» ефект операції симетрії\(g_i\). Наприклад, в\(C_{3v}\) точковій групі обернене\(C_3^+\) є\(C_3^-\).
Правило поєднання повинно бути асоціативним\[(A_i A_j )(A_k) = A_i(A_jA_k) \nonumber \] Або\(A(BC)=(AB)C\). Іншими словами, порядок операцій не повинен мати значення.

Теорія груп є важливою областю в математиці, і, на щастя, для хіміків математики вже зробили більшу частину роботи за нас. Поряд з формальним визначенням групи приходить всебічна математична база, яка дозволяє проводити суворе лікування симетрії в молекулярних системах і дізнатися про її наслідки.

Багато проблем, пов'язаних з операторами або операціями (наприклад, ті, що зустрічаються в квантовій механіці або теорії груп), можуть бути переформульовані з точки зору матриць. Будь-який з вас, хто раніше стикався з матрицями перетворення, буде знати, що операції симетрії, такі як обертання та відображення, можуть бути представлені матрицями. Виходить, що множина матриць, що представляють операції симетрії в групі, підпорядковується всім умовам, викладеним вище в математичному визначенні групи, а використання матричних уявлень операцій симетрії спрощує проведення розрахунків в теорії груп. Перш ніж ми дізнаємося, як використовувати матриці в теорії груп, ймовірно, буде корисно переглянути деякі основні визначення та властивості матриць.

*Ця сторінка була адаптована звідси (натисніть).