1.9: Дифузія

1. ДИФУЗІЇ

При будь-якій температурі, відмінній від абсолютного нуля, всі атоми, незалежно від їх агрегатного стану (газоподібний, рідкий або твердий), постійно знаходяться в русі. Так як рух частинок пов'язане з зіткненнями, шлях однієї частинки - зигзагоподібний. Однак агрегація «дифузійних» частинок має помітний дрейф від місць вищих до місць меншої концентрації (рис.1). З цієї причини дифузія відома як транспортне явище.

Рисунок 1. Масовий транспорт, дифузія як наслідок існуючих просторових відмінностей концентрації.

У кожній дифузійної реакції (тепловий потік, наприклад, також є дифузійним процесом) потік (речовини, тепла, електрики і т.д.) слідує загальному співвідношенню:

Потік = (провідність) х (рушійна сила)

У випадку атомної або молекулярної дифузії «провідність» називається дифузійністю або константою дифузії, і представлена символом D. З вищезазначених міркувань ми розуміємо, що ця константа дифузії (D) відображає рухливість дифузійних видів в даного середовища і відповідно приймає більші значення в газах, менші - в рідинях, і вкрай малі - в твердих тілах.

Рисунок 2 Градієнт концентрації (константа) у напрямку x

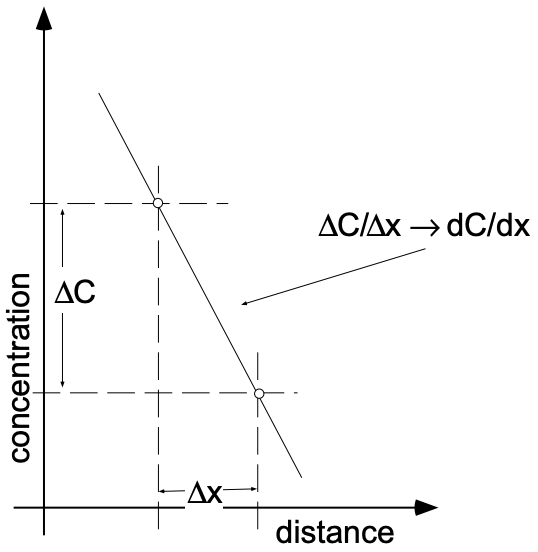
«Рушійною силою» для багатьох типів дифузії є існування градієнта концентрації. Термін «градієнт» описує варіацію заданої властивості як функцію відстані в напрямку x. Якщо матеріал проявляє лінійну зміну концентрації з відстанню в напрямку x, ми говоримо про постійний градієнт концентрації в напрямку x. Сам градієнт - це швидкість зміни концентрації з відстанню (dc/dx), яка така ж, як нахил графіка концентрації vs. положення\(\Delta c/\Delta x)\) (див. рис.2).

Сталий стан і нестаціонарна дифузія

Дифузійні процеси можна розділити на два типи: (а) стаціонарний стан і (б) нестаціонарний стан. Дифузія сталого стану відбувається з постійною швидкістю - тобто після запуску процесу кількість атомів (або молів), що перетинають заданий інтерфейс (потік), є постійним з часом. Це означає, що по всій системі dc/dx = постійна і dc/dt = 0.

Дифузія нестаціонарного стану - це залежний від часу процес, в якому швидкість дифузії є функцією часу. Таким чином, dc/dx змінюється в залежності від часу і dc/dt ≠ 0. Обидва типи дифузії описуються кількісно законами дифузії Фіка. Перший закон стосується як стаціонарного, так і нестаціонарного стану дифузії, тоді як другий закон стосується лише дифузії нестаціонарного стану.

2. ДИФУЗІЯ СТАЛОГО СТАНУ (ПЕРШИЙ ЗАКОН ФІКА)

Виходячи з вищезазначених міркувань, Перший закон Фіка може бути сформульований як:

\(\mathrm{J}=-\mathrm{D}\left(\dfrac{\mathrm{dc}}{\mathrm{dx}}\right)\)У словах: Дифузійний потік пропорційний існуючому градієнту концентрації.

Негативний знак у цьому співвідношенні вказує на те, що потік частинок відбувається в напрямку градієнта «вниз», тобто від областей вищих до областей меншої концентрації. Потік\(\mathrm{J}\) може бути заданий в одиницях атомів\(/ \mathrm{cm}^2 \mathrm{~s}\), молів/\(\mathrm{cm}^2 \mathrm{~s}\), або еквівалентах. Відповідно, дифузійність (D) прийматиме розміри\(\mathrm{cm}^2 / \mathrm{s}\), як видно з розмірного аналізу:

\(\mathrm{J}\left(\dfrac{\text { moles }}{\mathrm{cm}^2 \mathrm{~s}}\right)=-\mathrm{D}\left(\dfrac{\mathrm{dc}}{\mathrm{dx}}\right)\left(\dfrac{\text { moles } \cdot \mathrm{cm}^{-3}}{\mathrm{~cm}}\right)\)

Таким чином:\(D=\mathrm{cm}^2 / \mathrm{s}\)

Як і хімічні реакції, дифузія є термічно активованим процесом, і температурна залежність дифузії з'являється в дифузійності як рівняння «типу Арренія»:

\(D=D_0 e^{-E_a / R T}\)

де\(D_o\) (еквівалент\(A\) в раніше обговорюваної температурної залежності константи швидкості) включає такі фактори, як відстань стрибка, коливальна частота дифузійного виду і так далі. \(D, D_0\)Вибрані значення і\(E_a\) наведені в таблиці 1 (a) і (b).

ТАБЛИЦЯ 1

(a) Вибрані значення констант дифузії (D)

\ begin {вирівняний}
&\ begin {масив} {llrl}
\ підкреслення {\ text {дифузійна речовина}} &\ підкреслити {\ текст {Розчинник}} &\ підкреслити {T\ left ({} ^ {\ circ}\ mathrm {C}\ праворуч)} &\ підкреслення {D\ left (\ mathrm {~cm} ^2\ cdot\ mathrm {s} ^ {-1}\ праворуч)}\\
\ mathrm {Au} &\ математика {Cu} & 400 & 5\ раз 10^ {-13}\
\ mathrm {Cu}\ текст {(саморозсіюється)} & (\ математика {Cu}) & 650 & 3.2\ раз 10^ {-12}\
\ mathrm {C} &\ mathrm {Fe}\ текст {(FCC)} & 950 & 10^ {-7}\
\ text {Метанол} &\ mathrm {H} _2\ mathrm {O} & підсилювач; 18 & 1.4\ раз 10^ {-5}
\\ mathrm {O} _2 &\ текст {повітря} & 0 & 0.178\
\ mathrm {H} _2 &\ текст {повітря} & 0 & 0.611
\ кінець {масив}\
\ кінець {вирівняний}

(b)\(D_o\) Вибрані значення та\(E_a\) для дифузійних систем

Розчинена речовина	Розчинник (структура господаря)	\(\underline{D_o, \mathrm{cm}^2 \mathrm{s}}\)	\(\underline{E_a}\), Джоуль/крот
1. Вуглець	FCC залізо	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">0.2100	\ (\ підкреслення {e_a}\), кДжоуль/Моль">142
2. Вуглець	bcc залізо	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">0.0079	\ (\ підкреслення {e_a}\), кДжоуль/Моль">76
3. Залізо	FCC залізо	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">0.5800	\ (\ підкреслення {e_a}\), кДжоуль/Моль">185
4. Залізо	bcc залізо	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">5.8000	\ (\ підкреслення {e_a}\), кДжоуль/Моль">251
5. Нікель	FCC залізо	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) "> 0.5000	\ (\ підкреслення {e_a}\), кДжоуль/Моль">276
6. Марганець	FCC залізо	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">0.3500	\ (\ підкреслення {e_a}\), кДжоуль/Моль">283
7. Цинк	мідь	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">0.0330	\ (\ підкреслення {e_a}\), кДжоуль/Моль">159
8. Мідь	алюміній	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">2.0000	\ (\ підкреслення {e_a}\), кДжоуль/Моль">142
9. Мідь	мідь	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">11.0000	\ (\ підкреслення {e_a}\), кДжоуль/Моль">240
10. Сріблястий	срібло	\ (\ підкреслення {d_o,\ mathrm {см} ^2\ mathrm {s}}\) ">0.7200	\ (\ підкреслення {e_a}\), Джоуль/Моль">18

Типове застосування першого закону Фіка: Визначити швидкість, з якою гелій (He), що утримується при 5 атм і\(200^{\circ} \mathrm{C}\) в скляній колбі Pyrex\(50 \mathrm{~cm}\) діаметром і товщиною стінки (\(\mathrm{x}\))\(0.1 \mathrm{~cm}\), дифундує через Pyrex назовні. Припустимо, що тиск зовні трубки в усі часи залишається незначним (див. Рис. (Для дифузії газів це

Малюнок 3. Умови виведеннядифузії He зі скляної колби.

прийнято, хоча і не обов'язково, замінювати константу дифузії\(D\) постійною проникнення\(\mathrm{K}\), як правило, наведеної в одиницях\(\mathrm{cm}^2 / \mathrm{s} \cdot\) атм. Використовуючи газові закони,\(\mathrm{K}\) легко перетворюється на\(\mathrm{D}\) при бажанні.)

У теперішній системі

\(\mathrm{K}=1 \times 10^{-9} \mathrm{~cm}^2 / \mathrm{s} \cdot \mathrm{atm}\)

Тепер ми можемо встановити рівняння дифузії:

\ (J=-\ mathrm {K}\ left (\ frac {\ mathrm {dP}} {\ mathrm {dx}}\ праворуч)\ quad\ begin {вирівняний}
&\ text {(і працювати з тиском замість}\\
&\ текст {концентрацій)}
\ кінець {вирівняний}\)

Тепер ми можемо формально розділити змінні та інтегрувати:

\ почати {вирівняний}
J\ математика {x} &=-\ математика {kDp}\
\ int_ {\ mathrm {x} =0} ^ {\ mathrm {x} =0.1}\ mathrm {Jx} &=-\ int_ {\ mathrm {p} _2=5} ^ {p_1=0}\ mathm {kDP}\\
\ математика {J} &=\ математика {K}\ frac {5.0} {0.1}
\ кінець {вирівняний}

Ми можемо відмовитися від інтеграції, оскільки\((\mathrm{dP} / \mathrm{dx})=(\Delta \mathrm{P} / \Delta \mathrm{x})\) ми можемо негайно написати:

\ begin {вирівняний}
\ математика {J} (\ текст {загальна}) &=-\ математика {K}\ frac {\ Дельта\ математика {P}} {\ Дельта\ математика {x}}\ час\ mathrm {A} =5\ раз 10^ {-8}\ раз 7,9\\ час 10^3\
\ mathrm {~J} &=3.9\ раз 10^ {-4}? ?
\ end {вирівняний}

Одиниці потоку можуть бути отримані з розмірного аналізу:

\(\mathrm{J}=-\mathrm{K} \times \dfrac{\Delta \mathrm{P}}{\Delta \mathrm{x}} \times \mathrm{A}=\dfrac{\mathrm{cm}^2}{\mathrm{~s} \cdot \mathrm{atm}} \dfrac{\mathrm{atm}}{\mathrm{cm}} \dfrac{\mathrm{cm}^2}{1}=\dfrac{\mathrm{cm}^3}{\mathrm{~s}}\)

Сумарний потік дорівнює\(3.9 \times 10^{-4} \mathrm{~cm}^3 / \mathrm{s}\) (при обсязі газу, заданому для\(0^{\circ} \mathrm{C}\) і\(1 \mathrm{~atm}\)). Якби загальний витрата газу шляхом дифузії повинен був визначатися за заданий часовий проміжок, обсяг помножився б на зазначений час.

3. ДИФУЗІЯ НЕСТАЦІОНАРНОГО СТАНУ (ДРУГИЙ ЗАКОН ФІКА)

Кількісне лікування дифузійних процесів нестаціонарного стану сформульовано як рівняння з частинними похідними. Детально розглядати рівняння виходить за рамки 3.091, але ми можемо якісно розглянути другий закон і кількісно вивчити деякі відповідні рішення.

Різниця між стаціонарними і нестаціонарними умовами дифузії може бути легко візуалізована (рис.4). У першому випадку ми маємо, наприклад, дифузію газу

Рисунок 4 Дифузія стійкого стану та нестаціонарного стану

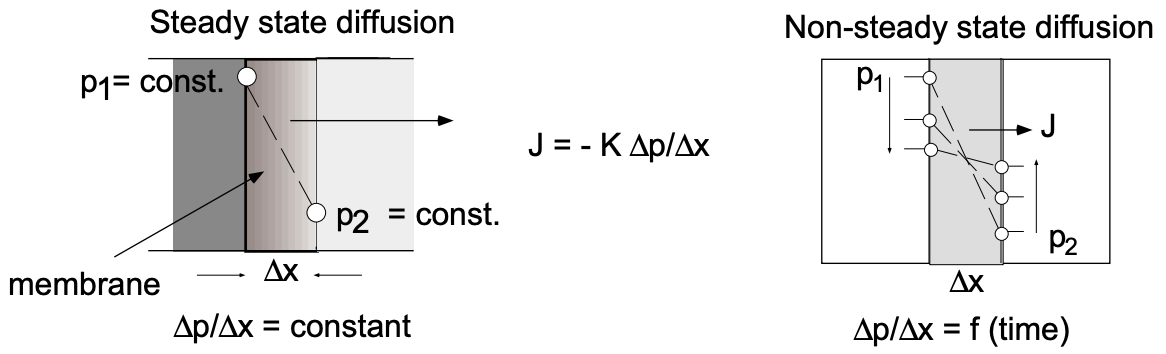
з нескінченного об'єму (\(\mathrm{P}_1\)const) через мембрану в нескінченний об'єм (\(\mathrm{P}_2\)const). Градієнт тиску на мембрані залишається постійним, як і дифузійний потік. У другому випадку ми маємо справу з дифузією з кінцевого об'єму через мембрану в скінченний об'єм. Тиск у задіяних резервуарах змінюється з часом, як і, отже, градієнт тиску через мембрану.

(Ви не зобов'язані бути знайомими з наступним виведенням Закону Другого Фіка, але ви повинні знати його остаточну форму.)

Розглянемо об'ємний елемент (між x і x+dx одиничної площі поперечного перерізу) мембрани, що розділяє два кінцеві об'єми, що беруть участь в дифузійній системі (рис.5). Потік даного матеріалу в об'ємний елемент за вирахуванням потоку з об'ємного елемента дорівнює швидкості накопичення матеріалу в цей об'ємний елемент:

\(J_x-J_{x+d x}=\dfrac{\partial \bar{c}}{\partial t} d x\)

[\(\bar{c}\)є середньою концентрацією в об'ємному елементі і\(\bar{c} d x\) є загальною кількістю дифузійного матеріалу в елементі в момент часу (t).]

Використовуючи серію Тейлора, ми можемо\(J_{x+d x}\) розширити\(x\) та отримати:

\(J_{x+d x}=J_x+\dfrac{\partial J_x}{\partial x} d x+\dfrac{\partial^2 J_x}{\partial x^2} \dfrac{d x^2}{2}+\ldots\)

Відповідно, як\(\mathrm{dx} \rightarrow 0\):

\(\dfrac{\partial}{\partial x}\left(D \dfrac{\partial c}{d x}\right)=\dfrac{\partial c}{\partial t}\)

і якщо\(D\) не змінюється\(x\) (що зазвичай буває), ми маємо формулювання Другого закону Фіка:

\(\dfrac{\partial \mathrm{C}}{\partial \mathrm{t}}=\mathrm{D} \dfrac{\partial^2 \mathrm{C}}{\partial \mathrm{x}^2} \quad \text { (Fick's Second Law) }\)

У фізичному плані цей зв'язок стверджує, що швидкість композиційної зміни пропорційна «швидкості зміни» градієнта концентрації, а не самому градієнту концентрації.

Рішення другого закону Фіка залежать від граничних умов, що накладаються конкретною проблемою, що цікавить. Як приклад розглянемо наступну проблему (зустрічається в багатьох твердотільних процесах):

Часто зустрічається ситуація - дифузія компонента 2 в нескінченну область матеріалу 1 (рис. 6) [планарна дифузія легуючих елементів в напівпровідники

Рисунок 6 Дифузія при постійній поверхневій концентрації; об'ємна концентрація компонента 2 на початку дифузії становить\(c_2^{\prime}\) (в а) і дорівнює нулю (в b).

для генерації перехідних пристроїв (p-n переходи, перехідні транзистори)]. Граничними умовами є: концентрація компонента (2) на поверхні твердої фази\((x=0)\) залишається постійною,\(c_2\) а концентрація компонента (2) у твердому тілі до дифузії рівномірно\(c_{2^{\prime}}\) (а). У цих граничних умовах розв'язання другого закону Фіка набуває вигляду:

\(\dfrac{c_2-c}{c_2-c_{2^{\prime}}}=\operatorname{erf}\left(\dfrac{x}{2 \sqrt{D t}}\right)\)

Якщо жоден компонент (2) спочатку не знаходиться в твердій матриці (1) (b), вищевказане рішення простіше:

\ почати {вирівняний}
\ dfrac {c_2-c} {c_2} &=\ ім'я оператора {erf}\ ліворуч (\ dfrac {x} {2\ sqrt {D t}}\ праворуч)\\
1-\ dfrac {c} {c_2} &=\ ім'я оператора {erf}\ ліворуч (\ dfrac {x} {2\ sqrt {D t}}\ праворуч)\
\ dfrac {c} {c_2} &=1-\ ім'я оператора {erf}\ ліворуч (\ dfrac {x} {2\ sqrt {D t}}\ праворуч)\\
\ dfrac {c} {c_2} &=\ ім'я оператора {erfc}\ ліворуч (\ dfrac {x} {2\ sqrt {D t}}\ праворуч)\\
c &=c_2\ text {erfc}\ ліворуч (\ dfrac {x} {2\ sqrt {D t}}\ праворуч)
\ кінець {вирівняний}

Аналіз показує, що остання форма розчину із законом Фіка пов'язує концентрацію (c) в будь-якому положенні (\(\mathrm{x}\)) (глибина проникнення в тверду матрицю) і час (t) з поверхневою концентрацією\(\left(c_2\right)\) і константою дифузії\((D)\). Терміни erf та erfc означають функцію помилки та додаткову функцію помилки відповідно - це функція помилки Гаусса, як таблична (як тригонометрична та експоненціальна функції) у математичних таблицях. Його граничними значеннями є:

\ begin {вирівняний}
&\ текст {erf} (0) &&= 0\\
&\ текст {erf} (\ infty) &&= 1\ quad &\ text {А для додаткової функції помилки:}\\
&\ text {erf} (-\ infty) &&=-1\ quad &\ text {erfc = (1-erf)}
\ кінець {вирівняний}

Інший погляд на вищезгадане рішення рівняння дифузії показує, що концентрація (c) компонента (2) у твердому тілі виражається через функцію похибки аргументу\(x / 2 \sqrt{D t}\). Щоб визначити, на якій глибині з'явиться та чи інша\(\left(\mathrm{c}^*\right)\) концентрація (2), підставляємо цю концентрацію на (c) і отримуємо:

\(\dfrac{c^*}{c_2}=\operatorname{erfc}\left(\dfrac{x}{2 \sqrt{D t}}\right)=K\)

Оскільки функція помилки є константою, її аргумент також повинен бути константою:

Рисунок 7 Просування фронту концентрації (c*) як функція триме

\(\dfrac{x}{2 \sqrt{D t}}=K^{\prime}\)

Тому при заданих граничних умовах:

\ почати {вирівняний}
&x = k^ {\ прайм} 2\ sqrt {D t}\\
&x = k^ {\ прайм}\ cdot\ sqrt {D t}\\
&x\ propto\ sqrt {t}
\ кінець {вирівняний}

Встановлено, що глибина проникнення заданої концентрації пропорційна квадратному кореню часу дифузії.

4. САМОДИФУЗІЇ

Як було зазначено раніше, тепловий рух атомів у решітці є випадковим процесом і як такий призведе до локальних переміщень окремих атомів. Це випадкове переміщення атомів всередині решітки (самодифузія), яке не пов'язане з жодними існуючими градієнтами концентрації, може бути легко продемонстровано за допомогою «радіоактивних елементів». Наприклад, нікель з'являється в природі у вигляді декількох «стабільних ізотопів»:

\(\mathrm{Ni}_{28}^{58}, \mathrm{Ni}_{28}^{60}, \mathrm{Ni}_{28}^{61}, \mathrm{Ni}_{28}^{62}\)і\(\mathrm{Ni}_{28}^{64}\)

Якщо\(\mathrm{Ni}_{28}^{58}\) опромінювати нейтронами в ядерному реакторі, він захопить нейтрон і стане\(\mathrm{Ni}_{28}^{59}\) радіоактивним (радіоізотоп).

\(\mathrm{Ni}_{28}^{58}+\mathrm{n} \rightarrow \mathrm{Ni}_{28}^{59} \rightarrow \mathrm{Co}_{27}^{59}+\gamma+\beta\)

Нікель 59 характеризується своєю нестабільністю, яка призводить до випромінювання\(\beta\) та\(\gamma\) випромінювання, з періодом напіврозпаду\(8 \times 10^4\) років. Оскільки це випромінювання може вимірюватися відповідними детекторами випромінювання, його можна використовувати в\(\mathrm{Ni}_{59}\) якості «елемента трасування» для досліджень самодифузії.

Радіоактивний нікель (який ідентичний звичайному нікелю за винятком його радіоактивних властивостей) гальванічним покриттям на нормальний нікель. Цей зразок згодом поміщають у піч і нагрівають до температури плавлення протягом тривалого періоду часу. Після видалення зразка його розрізають на зрізи паралельно поверхні, на якій містився радіоактивний мікроелемент. За допомогою детектора випромінювання тепер можна показати, що той\(\mathrm{Ni}_{59}\), який спочатку був лише на поверхні, розсіяний у сипучий матеріал, тоді як одночасно деякий об'ємний нікель має протирозсіяний в іншому напрямку. Якщо цей зразок піддається термічній обробці протягом набагато більш тривалого часу, розтин і підрахунок виявлять повністю рівномірний розподіл елемента радіотрактора. Таким чином, можна показати, що самодифузія дійсно відбувається в твердих тілах, а кількісні вимірювання з елементами трасування навіть дозволяють визначити коефіцієнти самодифузії.

5. ДИФУЗІЙНІ МЕХАНІЗМИ

Процес дифузії в інтерстиціальних твердих розчині, як у вуглецю в залізі, можна легко зрозуміти в результаті значних відмінностей атомних діаметрів. Однак той факт, що\(\mathrm{Au}\) дифузує швидше,\(\mathrm{Pb}\) ніж\(\mathrm{NaCl}\) дифузує у воді,\(15^{\circ} \mathrm{C}\) не може бути легко пояснений. Величина спостережуваної енергії активації вказує на те, що механізм, за допомогою якого атоми просто змінюються місцями один з одним, повинен бути виключений. Більш розумні механізми запропонували Френкель і Шотткі. Вони запропонували існування точкових дефектів (вакансій) у кристалах, які забезпечують механізм, за допомогою якого атоми можуть рухатися (дифузно) всередині кристала. Концентрацію таких вакансій, як ви пам'ятаєте, можна розрахувати з простих статистичних розрахунків.

У більшості твердих тіл ми маємо справу не з монокристалами, а з полікристалічними матеріалами, які містять велику кількість меж зерен (внутрішніх поверхонь). Як і очікувалося, швидкість дифузії вздовж кордонів зерен значно вища, ніж при об'ємній дифузії (\(D_{\text {volume }}<D_{\text {g-boundary }}\)). Нарешті, поверхнева дифузія, яка має місце на всіх зовнішніх поверхнях, ще вище\(\left(D_{\text {volume }}<D_{\text {g-boundary }}<D_{\text {surface }}\right)\). Відповідними енергіями активації для дифузії є:

\(E_a\)\(<E_a\)Обсяг граничного\(<E_a\) зерен поверхні

Дифузія в неметалах

У неметалевих системах дифузія відбувається тими ж механізмами, що і в металевих системах. Наприклад, кисень дифундує через багато оксидів шляхом міграції вакансій. У кристалічних оксидах, а також у силікатних стеклах встановлено, що кисень розсіюється набагато швидше, ніж металевий іон. У стеклах, що містять атоми лугу\(\left(\mathrm{Na}^{+}, \mathrm{K}^{+}\right)\), відповідні швидкості дифузії становлять:

\[D_{\text {alkali }}>D_{\text {oxygen }}>D_{\text {silicon }}\]

що відповідає відмінностям міцності склеювання. У полімерних матеріалах дифузія вимагає руху великих молекул, оскільки внутрішньомолекулярне з'єднання набагато міцніше міжмолекулярного зв'язку. Цей факт пояснює, що швидкості дифузії в таких матеріалах відносно невеликі.

Газова дифузія в твердих тілах

Деякі гази, такі як водень і гелій, дифундують через деякі метали з легкістю навіть при кімнатній температурі. Гелій, наприклад, буде розсіюватися через кварц і сталь і обмежує граничний вакуум, який можна отримати в надвисоких вакуумних системах. Водень аналогічно легко розсіюється наскрізь\(\mathrm{Ni}\) при підвищених температурах. \(\mathrm{H}_2\)також дифузує з високою швидкістю через паладій - явище, яке широко використовується для очищення водню, оскільки цей матеріал непроникний для інших газів.

ТАБЛИЦЯ 2: Функція помилки

\(z\)	\(erf(z)\)	\(z\)	\(erf(z)\)
\ (z\) ">0	\ (ерф (z)\) ">0	\ (z\) ">0.85	\ (ерф (з)\) ">0.7707
\ (z\) ">0,025	\ (ерф (з)\) ">0.0282	\ (z\) ">0.90	\ (ерф (з)\) ">0.7970
\ (z\) ">0,05	\ (ерф (з)\) ">0,0564	\ (z\) ">0,95	\ (ерф (з)\) ">0.8209
\ (z\) ">0,10	\ (ерф (з)\) ">0,1125	\ (z\) ">1.0	\ (ерф (з)\) ">0.8427
\ (z\) ">0,15	\ (ерф (з)\) ">0.1680	\ (z\) ">1.1	\ (ерф (з)\) ">0.8802
\ (z\) ">0.20	\ (ерф (з)\) ">0.2227	\ (z\) ">1.2	\ (ерф (з)\) ">0.9103
\ (z\) ">0,25	\ (ерф (з)\) ">0.2763	\ (z\) ">1.3	\ (ерф (з)\) ">0.9340
\ (z\) ">0.30	\ (ерф (з)\) ">0.3286	\ (z\) ">1.4	\ (ерф (з)\) ">0.9523
\ (z\) ">0.35	\ (ерф (з)\) ">0.3794	\ (z\) ">1.5	\ (ерф (з)\) ">0.9661
\ (z\) ">0.40	\ (ерф (з)\) ">0.4234	\ (z\) ">1.6	\ (ерф (з)\) ">0.9763
\ (z\) ">0.45	\ (ерф (з)\) ">0.4755	\ (z\) ">1.7	\ (ерф (з)\) ">0.9838
\ (z\) ">0,50	\ (ерф (з)\) ">0,5205	\ (z\) ">1.8	\ (ерф (з)\) ">0.9891
\ (z\) ">0,55	\ (ерф (з)\) ">0.5633	\ (z\) ">1.9	\ (ерф (з)\) ">0.9928
\ (z\) ">0.60	\ (ерф (з)\) ">0.6039	\ (z\) ">2.0	\ (ерф (з)\) ">0.9953
\ (z\) ">0,65	\ (ерф (з)\) ">0.6420	\ (z\) ">2.2	\ (ерф (з)\) ">0.9981
\ (z\) ">0.70	\ (ерф (з)\) ">0.6778	\ (z\) ">2.4	\ (ерф (з)\) ">0.9993
\ (z\) ">0,75	\ (ерф (з)\) ">0.7112	\ (z\) ">2.6	\ (ерф (з)\) ">0.9998
\ (z\) ">0,80	\ (ерф (з)\) ">0.7421	\ (z\) ">2.8	\ (ерф (з)\) ">0.9999

 

ДЖЕРЕЛО: Значення erf (z) до 15 місць, з кроком z 0,0001, можна знайти в Проекті математичних таблиць, «Таблиця функцій ймовірності.», т. 1, Федеральне агентство робіт, Управління проектів робіт, Нью-Йорк, 1941. Обговорення оцінки erf (z), його похідних і інтегралів, з короткою таблицею дано H. Carslaw і J. Jaeger, в додатку 2 «Провідність тепла в твердих тілах», Oxford University Press, Fair Lawn, Нью-Джерсі, 1959.