1.6: Математична обробка результатів вимірювань
- Page ID
- 22660
БІРЮЩ
- Поясніть мірний аналіз (факторна мітка) підхід до математичних розрахунків за участю величин.
- Опишіть, як використовувати аналіз розмірів для здійснення одиничних перетворень для заданої властивості та обчислень, що включають два або більше властивостей.
- Перетворення між трьома основними одиницями температури: за Фаренгейтом, Цельсієм та Кельвіном.
Часто трапляється так, що кількість відсотків може бути нелегко (або навіть можливо) виміряти безпосередньо, але замість цього повинна бути обчислена з інших безпосередньо виміряних властивостей та відповідних математичних зв'язків. Наприклад, розглянемо вимірювання середньої швидкості спортсмена, що біжить спринтами. Зазвичай це досягається шляхом вимірювання часу, необхідного спортсмену для бігу від стартової лінії до фінішу, і відстані між цими двома лініями, а потім обчислення швидкості з рівняння, яке пов'язує ці три властивості:
\[\mathrm{speed=\dfrac{distance}{time}} \nonumber \]
Спринтер олімпійської якості може пробігти 100 м приблизно за 10 с, що відповідає середній швидкості
\[\mathrm{\dfrac{100\: m}{10\: s}=10\: m/s} \nonumber \]
Зверніть увагу, що ця проста арифметика передбачає поділ чисел кожної виміряної кількості, щоб отримати кількість обчислюваної кількості (100/10 = 10) і аналогічним чином ділення одиниць кожної виміряної кількості, щоб отримати одиницю обчислюваної кількості (м/с = м/с). Тепер розглянемо використання цього ж відношення для прогнозування часу, необхідного людині, що біжить з цією швидкістю, щоб пройти відстань 25 м Використовується таке ж відношення між трьома властивостями, але в цьому випадку дві надані величини - це швидкість (10 м/с) і відстань (25 м). Щоб отримати шукане майно, час, рівняння необхідно переставити відповідним чином:
\[\mathrm{time=\dfrac{distance}{speed}} \nonumber \]
Потім час можна обчислити як:
\[\mathrm{\dfrac{25\: m}{10\: m/s}=2.5\: s} \nonumber \]
Знову ж арифметика на цифрах (25/10 = 2,5) супроводжувалася тією ж арифметикою на одиницях (м/м/с = s) для отримання числа і одиниці результату, 2,5 с. зверніть увагу, що, як і для чисел, коли одиниця ділиться на однакову одиницю (в даному випадку м/м), результат «1» —або, як прийнято формулювати, одиниці» скасувати».
Ці розрахунки є прикладами універсального математичного підходу, відомого як мірний аналіз (або метод фактор-мітка). Розмірний аналіз базується на цій передумові: одиниці величин повинні піддаватися тим же математичним операціям, що й пов'язані з ними числа. Цей метод може бути застосований для обчислень, починаючи від простих конверсій одиниць до більш складних, багатоступінчастих розрахунків, що включають кілька різних величин.
Коефіцієнти перетворення та розмірний аналіз
Як коефіцієнт перетворення одиниць може використовуватися відношення двох еквівалентних величин, виражених різними одиницями вимірювання. Наприклад, довжини 2,54 см і 1 дюйм. еквівалентні (за визначенням), і тому коефіцієнт перетворення одиниці може бути отриманий з співвідношення,
\[\mathrm{\dfrac{2.54\: cm}{1\: in.}\:(2.54\: cm=1\: in.)\: or\: 2.54\:\dfrac{cm}{in.}} \nonumber \]
Кілька інших часто використовуваних коефіцієнтів перерахунку наведені в табл\(\PageIndex{1}\).
| Довжина | Обсяг | Маса |
|---|---|---|
| 1 м = 1.0936 ярд | 1 Л = 1.0567 ат | 1 кг = 2,2046 фунта |
| 1 дюйм = 2,54 см (точний) | 1 кварт = 0.94635 л | 1 фунт = 453,59 г |
| 1 км = 0,62137 миль | 1 фут 3 = 28.317 л | 1 (авоірдупуа) унція = 28,349 г |
| 1 миль = 1609.3 м | 1 ст.л. = 14,787 мл | 1 (тройська) унція = 31.103 г |
Коли ми множимо кількість (наприклад, відстань у дюймах) на відповідний коефіцієнт перетворення одиниць, ми перетворюємо кількість на еквівалентне значення з різними одиницями (наприклад, відстань у сантиметрах). Наприклад, вертикальний стрибок баскетболіста в 34 дюйма може бути перетворений в сантиметри за допомогою:
\[\mathrm{34\: \cancel{in.} \times \dfrac{2.54\: cm}{1\:\cancel{in.}}=86\: cm} \nonumber \]
Оскільки ця проста арифметика включає величини, передумова розмірного аналізу вимагає, щоб ми помножили як числа, так і одиниці. Числа цих двох величин множаться, щоб отримати кількість продукту, 86, тоді як одиниці множаться на вихід
\[\mathrm{\dfrac{in.\times cm}{in.}}. \nonumber \]
Так само, як і для чисел, співвідношення однакових одиниць також чисельно дорівнює одиниці,
\[\mathrm{\dfrac{in.}{in.}=1} \nonumber \]
а одиниця виробу при цьому спрощується до см. (Коли однакові одиниці діляться, щоб дати коефіцієнт 1, вони кажуть «скасувати».) Використовуючи аналіз розмірів, ми можемо визначити, що коефіцієнт перетворення одиниць був встановлений правильно, перевіривши, що вихідна одиниця скасує, а результат буде містити шукану (перетворену) одиницю.
Маса змагань фрісбі становить 125 м Переведіть його масу в унції за допомогою коефіцієнта перетворення одиниць, отриманого з співвідношення 1 унція = 28,349 г (табл.\(\PageIndex{1}\)).
Рішення
Якщо у нас є коефіцієнт перетворення, ми можемо визначити масу в кілограмах, використовуючи рівняння, подібне до того, яке використовується для перетворення довжини з дюймів в сантиметри.
\[x\:\mathrm{oz=125\: g\times unit\: conversion\: factor}\nonumber \]
Пишемо коефіцієнт перетворення одиниць в двох його формах:
\[\mathrm{\dfrac{1\: oz}{28.349\: g}\:and\:\dfrac{28.349\: g}{1\: oz}}\nonumber \]
Правильний коефіцієнт перетворення одиниць - це співвідношення, яке скасовує одиниці грамів і залишає унції.
\ [\ begin {align*}
x\:\ ce {oz} &=\ mathrm {125\:\ скасувати {г}\ раз\ фрак {1\: унція} {28.349\:\ скасувати {г}}}\\
&=\ mathrm {\\ ліво (\ dfrac {125} {28.349}\ праворуч)\ :унція}\\
&=\ mathr m {4.41\: oz\: (три\: значні\: цифри)}
\ кінець {align*}\ nonumber\]
Перетворіть обсяг 9.345 qt в літри.
- Відповідь
-
8.844 Л
Крім простих одиничних перетворень, метод фактор-мітка може бути використаний для вирішення більш складних завдань, пов'язаних з обчисленнями. Незалежно від деталей, основний підхід однаковий - всі фактори, що беруть участь у розрахунку, повинні бути належним чином орієнтовані на те, щоб гарантувати, що їх мітки (одиниці) відповідним чином скасують та/або об'єднають, щоб отримати бажану одиницю в результаті. Ось чому його називають методом фактор-міток. Оскільки ваше вивчення хімії триває, ви зіткнетеся з багатьма можливостями застосувати цей підхід.
Яка щільність звичайного антифризу в одиницях г/мл? 4.00-qt зразок антифризу важить 9,26 фунтів.
Рішення
Так як\(\mathrm{density=\dfrac{mass}{volume}}\), нам потрібно розділити масу в грамах на обсяг в мілілітрах. Загалом: кількість одиниць В = кількість одиниць коефіцієнта перетворення\(\times\) одиниць А. Необхідні коефіцієнти перерахунку наведені в таблиці 1.7.1:1 фунт = 453,59 г; 1 Л = 1,0567 qt; 1 л = 1000 мл. Ми можемо перетворити масу з фунтів в грами за один крок:
\[\mathrm{9.26\:\cancel{lb}\times \dfrac{453.59\: g}{1\:\cancel{lb}}=4.20\times 10^3\:g}\nonumber \]
Нам потрібно використовувати два кроки, щоб перетворити обсяг з кварт в мілілітри.
- Перетворити кварти в літри.
\[\mathrm{4.00\:\cancel{qt}\times\dfrac{1\: L}{1.0567\:\cancel{qt}}=3.78\: L}\nonumber \]
- Перетворити літри в мілілітри.
\[\mathrm{3.78\:\cancel{L}\times\dfrac{1000\: mL}{1\:\cancel{L}}=3.78\times10^3\:mL}\nonumber \]
Потім,
\[\mathrm{density=\dfrac{4.20\times10^3\:g}{3.78\times10^3\:mL}=1.11\: g/mL}\nonumber \]
Крім того, розрахунок може бути налаштований таким чином, що послідовно використовує три коефіцієнти перетворення одиниць:
\[\mathrm{\dfrac{9.26\:\cancel{lb}}{4.00\:\cancel{qt}}\times\dfrac{453.59\: g}{1\:\cancel{lb}}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\:\cancel{L}}{1000\: mL}=1.11\: g/mL}\nonumber \]
Який обсяг в літрах 1.000 унцій, враховуючи, що 1 л = 1.0567 qt і 1 qt = 32 унції (точно)?
- Відповідь
-
\(\mathrm{2.956\times10^{-2}\:L}\)
Під час руху з Філадельфії до Атланти, відстань близько 1250 км, а 2014 Lamborghini Aventador Roadster використовує 213 л бензину.
- Яку (середню) економію палива, в милі на галон, отримав Roadster під час цієї поїздки?
- Якщо бензин коштує 3,80 долара за галон, яка вартість палива для цієї поїздки?
Рішення
(a) Спочатку перетворюємо відстань від кілометрів до миль:
\[\mathrm{1250\: km\times\dfrac{0.62137\: mi}{1\: km}=777\: mi}\nonumber \]
а потім перетворити об'єм з літрів в галони:
\[\mathrm{213\:\cancel{L}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\: gal}{4\:\cancel{qt}}=56.3\: gal}\nonumber \]
Потім,
\[\mathrm{(average)\: mileage=\dfrac{777\: mi}{56.3\: gal}=13.8\: miles/gallon=13.8\: mpg}\nonumber \]
Крім того, розрахунок можна налаштувати таким чином, щоб послідовно використовувалися всі коефіцієнти перетворення, наступним чином:
\[\mathrm{\dfrac{1250\:\cancel{km}}{213\:\cancel{L}}\times\dfrac{0.62137\: mi}{1\:\cancel{km}}\times\dfrac{1\:\cancel{L}}{1.0567\:\cancel{qt}}\times\dfrac{4\:\cancel{qt}}{1\: gal}=13.8\: mpg}\nonumber \]
(б) Використовуючи раніше розрахований обсяг в галонів, знаходимо:
\[\mathrm{56.3\: gal\times\dfrac{$3.80}{1\: gal}=$214}\nonumber \]
Toyota Prius Hybrid використовує 59.7 л бензину для їзди з Сан-Франциско до Сіетла, відстань 1300 км (дві значущі цифри).
- Яку (середню) економію палива, в милі на галон, отримав Prius під час цієї поїздки?
- Якщо бензин коштує 3,90 долара за галон, яка вартість палива для цієї поїздки?
- Відповідь на
-
51 миль/год
- Відповідь б
-
$62
Перетворення одиниць температури
Ми використовуємо слово температура для позначення гарячості або холодності речовини. Одним із способів вимірювання зміни температури є використання того факту, що більшість речовин розширюються, коли їх температура збільшується, і стискаються, коли їх температура знижується. Ртуть або спирт в загальному скляному термометрі змінює свій обсяг у міру зміни температури. Оскільки обсяг рідини змінюється більше, ніж обсяг скла, ми можемо бачити, як рідина розширюється, коли вона стає теплішою, і стискається, коли стає прохолодніше.
Щоб відзначити шкалу на термометрі, нам знадобиться набір еталонних значень: Два найбільш часто використовуваних - це температури замерзання і кипіння води при заданому атмосферному тиску. За шкалою Цельсія 0° C визначається як температура замерзання води і 100° C як температура кипіння води. Простір між двома температурами ділиться на 100 рівних інтервалів, які ми називаємо градусами. За шкалою Фаренгейта температура замерзання води визначається як 32° F, а температура кипіння - 212° F, простір між цими двома точками на термометрі Фаренгейта розділений на 180 рівних частин (градусів).
Визначення температурних шкал Цельсія і Фаренгейта, як описано в попередньому пункті, призводить до дещо складнішої залежності між значеннями температури на цих двох шкалах, ніж для різних одиниць вимірювання для інших властивостей. Більшість одиниць виміру для даної властивості прямо пропорційні один одному (y = mx). Використання звичних одиниць довжини в якості одного з прикладів:
\[\mathrm{length\: in\: feet=\left(\dfrac{1\: ft}{12\: in.}\right)\times length\: in\: inches} \nonumber \]
де
- y = довжина в футах,
- x = довжина в дюймах, і
- константа пропорційності, m, - коефіцієнт перетворення.
Температурні шкали Цельсія і Фаренгейта, однак, не мають спільної нульової точки, і тому зв'язок між цими двома шкалами є лінійною, а не пропорційною (\(y = mx + b\)). Отже, перетворення температури з однієї з цих шкал в іншу вимагає більш ніж простого множення на коефіцієнт перетворення, m, він також повинен враховувати відмінності в нульових точках шкали (\(b\)).
Лінійне рівняння, що стосується температур Цельсія та Фаренгейта, легко виводиться з двох температур, що використовуються для визначення кожної шкали. Представляючи температуру за Цельсієм\(y\), а температуру\(x\) Фаренгейта, як, нахил\(m\), обчислюється таким чином:
\[\begin{align*} m &=\dfrac{\Delta y}{\Delta x} \\[4pt] &= \mathrm{\dfrac{212\: ^\circ F - 32\: ^\circ F}{100\: ^\circ C-0\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{180\: ^\circ F}{100\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{9\: ^\circ F}{5\: ^\circ C} }\end{align*} \nonumber \]
Y-перехоплення рівняння, b, потім обчислюється за допомогою будь-якої з еквівалентних пар температур (100° C, 212° F) або (0° C, 32° F), як:
\[\begin{align*} b&=y-mx \\[4pt] &= \mathrm{32\:^\circ F-\dfrac{9\:^\circ F}{5\:^\circ C}\times0\:^\circ C} \\[4pt] &= \mathrm{32\:^\circ F} \end{align*} \nonumber \]
Рівняння, що стосується температурних шкал, тоді:
\[\mathrm{\mathit{T}_{^\circ F}=\left(\dfrac{9\:^\circ F}{5\:^\circ C}\times \mathit{T}_{^\circ C}\right)+32\:^\circ C} \nonumber \]
Скорочена форма цього рівняння, що опускає одиниці виміру, є:
\[\mathrm{\mathit{T}_{^\circ F}=\dfrac{9}{5}\times \mathit{T}_{^\circ C}+32} \nonumber \]
Перестановка цього рівняння дає форму, корисну для перетворення з Фаренгейта в Цельсія:
\[\mathrm{\mathit{T}_{^\circ C}=\dfrac{5}{9}(\mathit{T}_{^\circ F}+32)} \nonumber \]
Як вже говорилося раніше в цьому розділі, одиницею температури СІ є Кельвін (K). На відміну від шкал Цельсія і Фаренгейта, шкала Кельвіна - це абсолютна температурна шкала, в якій 0 (нуль) К відповідає найнижчій температурі, яку теоретично можна досягти. Відкриття зв'язку між обсягом і температурою газу на початку XIX століття припустило, що обсяг газу буде дорівнює нулю при −273,15° C. 1848 британський фізик Вільям Томпсон, який пізніше прийняв титул лорда Кельвіна, запропонував абсолютну температурну шкалу, засновану на цій концепції (далі розгляду цієї теми наведено в цьому тексті главі про гази).
Температура замерзання води за цією шкалою становить 273,15 К, а її температура кипіння 373,15 К. Зверніть увагу, що числова різниця в цих двох еталонних температурах становить 100, така ж, як і для шкали Цельсія, і тому лінійне співвідношення між цими двома температурними шкалами буде демонструвати нахил\(\mathrm{1\:\dfrac{K}{^\circ\:C}}\). Дотримуючись того ж підходу, рівняння для перетворення між шкалами температури Кельвіна і Цельсія виводяться такими:
\[T_{\ce K}=T_{\mathrm{^\circ C}}+273.15 \nonumber \]
\[T_\mathrm{^\circ C}=T_{\ce K}-273.15 \nonumber \]
273.15 в цих рівняннях було визначено експериментально, тому воно не є точним. \(\PageIndex{1}\)На малюнку показана залежність між трьома температурними шкалами. Нагадаємо, що ми не використовуємо знак градуса з температурами за шкалою Кельвіна.
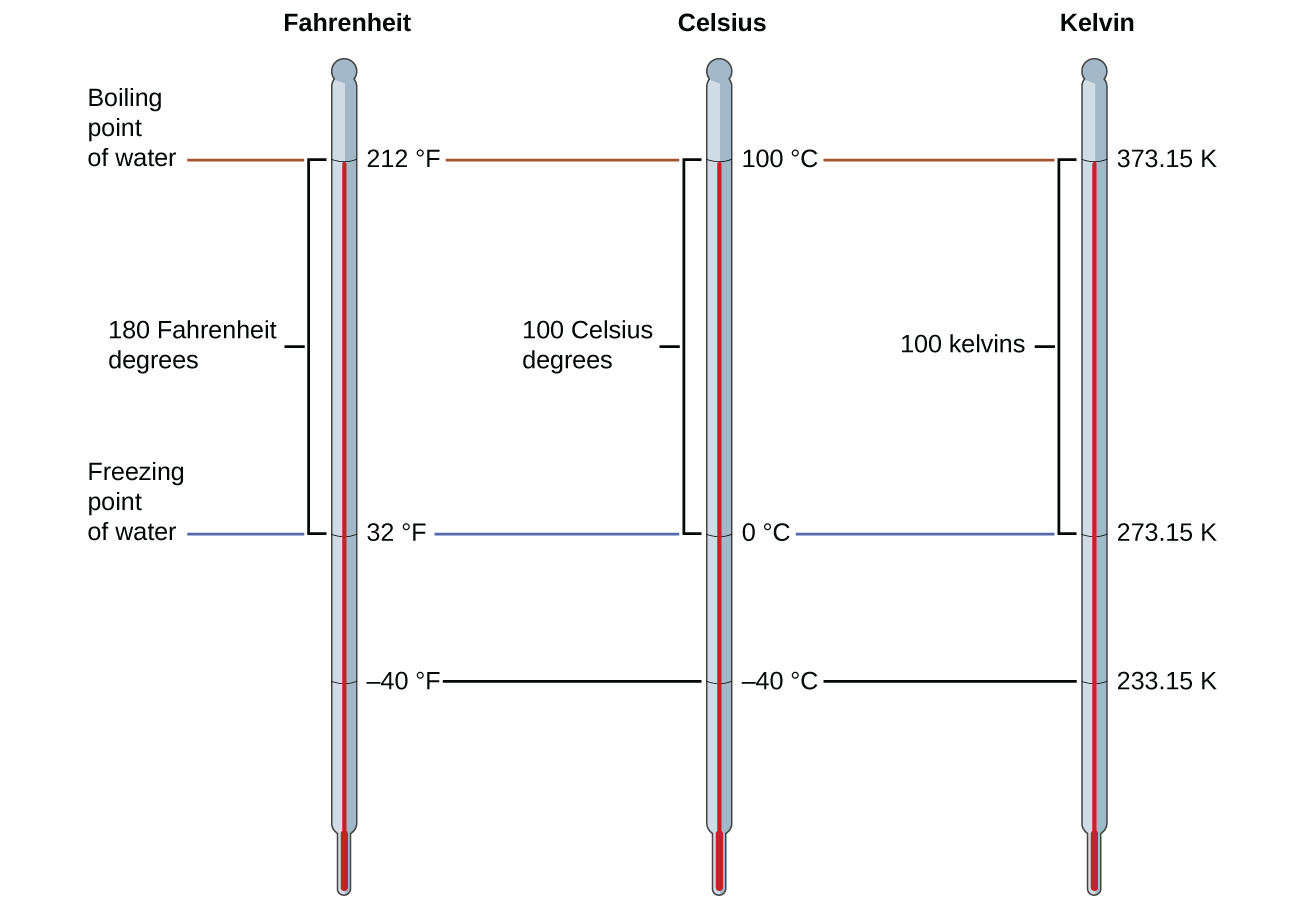
Хоча шкала температури Кельвіна (абсолютна) є офіційною шкалою температури СІ, Цельсія зазвичай використовується в багатьох наукових контекстах і є шкалою вибору для ненаукових контекстів майже у всіх областях світу. Дуже мало країн (США та їх території, Багамські острови, Беліз, Кайманові острови та Палау) все ще використовують Фаренгейт для погоди, медицини та кулінарії.
Нормальна температура тіла була загальноприйнята як 37,0° C (хоча вона варіюється в залежності від часу доби і способу вимірювання, а також серед осіб). Що це за температура за шкалою Кельвіна і за шкалою Фаренгейта?
Рішення
\[\mathrm{K= {^\circ C}+273.15=37.0+273.2=310.2\: K}\nonumber \]
\[\mathrm{^\circ F=\dfrac{9}{5}\:{^\circ C}+32.0=\left(\dfrac{9}{5}\times 37.0\right)+32.0=66.6+32.0=98.6\: ^\circ F}\nonumber \]
Перетворіть 80.92° C до K і° F.
- Відповідь
-
354.07 КМ, 177.7 °F
Випікання готової піци вимагає температури духовки 450° F Якщо ви перебуваєте в Європі, а ваш термометр духовки використовує шкалу Цельсія, яка настройка? Яка температура Кельвіна?
Рішення
\[\mathrm{^\circ C=\dfrac{5}{9}(^\circ F-32)=\dfrac{5}{9}(450-32)=\dfrac{5}{9}\times 418=232 ^\circ C\rightarrow set\: oven\: to\: 230 ^\circ C}\hspace{20px}\textrm{(two significant figures)}\nonumber \]
\[\mathrm{K={^\circ C}+273.15=230+273=503\: K\rightarrow 5.0\times 10^2\,K\hspace{20px}(two\: significant\: figures)}\nonumber \]
Перетворіть 50° F до° C і K.
- Відповідь
-
10 °C, 280 КМ
Резюме
Вимірювання проводяться з використанням різноманітних одиниць. Часто корисно або необхідно перетворити виміряну величину з однієї одиниці в іншу. Ці перетворення здійснюються за допомогою одиничних коефіцієнтів перетворення, які виводяться за допомогою простих застосувань математичного підходу, який називається методом фактор-мітка або розмірним аналізом. Ця стратегія також використовується для обчислення шуканих величин за допомогою вимірюваних величин та відповідних математичних відносин.
Ключові рівняння
- \(T_\mathrm{^\circ C}=\dfrac{5}{9}\times T_\mathrm{^\circ F}-32\)
- \(T_\mathrm{^\circ F}=\dfrac{9}{5}\times T_\mathrm{^\circ C}+32\)
- \(T_\ce{K}={^\circ \ce C}+273.15\)
- \(T_\mathrm{^\circ C}=\ce K-273.15\)
Глосарій
- розмірний аналіз
- (також метод фактор-мітка) універсальний математичний підхід, який може бути застосований до обчислень, починаючи від простих одиничних перетворень до більш складних, багатоступінчастих розрахунків, що включають кілька різних величин
- Фаренгейт
- одиниця температури; вода замерзає при 32° F і кипить при 212° F за цією шкалою
- коефіцієнт перетворення одиниць
- співвідношення еквівалентних величин, виражених різними одиницями; використовується для перетворення з однієї одиниці в іншу одиницю
