17.4: Механізми реакції

Last updated
Save as PDF

Page ID: 18995

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Переконайтеся, що ви добре розумієте наступні основні ідеї, які були представлені вище. Особливо важливо, щоб ви знали точні значення всіх зелених термінів в контексті цієї теми.

Поясніть, що мається на увазі під механізмом реакції.
Визначте елементарну реакцію, і вкажіть, чим вона відрізняється від звичайної чистої хімічної реакції.
Намалюйте енергетичну діаграму активації для багатоступінчастого механізму, що включає крок визначення швидкості, і пов'яжіть це з енергією активації загальної реакції.
Запишіть вираз закону швидкості для двоступеневого механізму, в якому константи швидкості мають значно різні величини.
Напишіть вираз закону швидкості для триступеневої реакції, в якій один крок є швидким рівновагою, а інші два ступені мають значно різні величини.
Визначте ланцюгову реакцію та перерахуйте деякі з різних видів кроків, які буде включати така реакція.
Визначте розгалужену ланцюгову реакцію і поясніть, як такі реакції можуть призвести до вибухів.

Тепер ми готові відкрити «чорний ящик», який лежить між реагентами і продуктами чистої хімічної реакції. Те, що ми знаходимо всередині, може бути не дуже гарним, але це завжди цікаво, оскільки воно дає нам опис того, як відбуваються хімічні реакції.

Механізм хімічної реакції - це послідовність реальних подій, які відбуваються у міру перетворення молекул реагентів в продукти. Кожна з цих подій являє собою елементарний крок, який може бути представлений як об'єднання дискретних частинок («зіткнення») або як розпад молекули («дисоціація») на більш прості одиниці. Молекулярна сутність, що виникає з кожного етапу, може бути кінцевим продуктом реакції, або вона може бути проміжною - видом, який створюється на одному елементарному етапі і руйнується на наступному етапі, і тому не відображається в рівнянні чистої реакції.

Для прикладу механізму розглянемо розкладання діоксиду азоту на оксид азоту і кисень. Чисте збалансоване рівняння

\[\ce{2 NO2(g) → 2 NO(g) + O2(g)} \nonumber\]

Вважається, що механізм цієї реакції передбачає наступні два елементарних етапи:

\[ \begin{align*} \ce{2 NO2} &→ \ce{NO3 + NO} \label{step 1} \\[4pt] \ce{NO3} &→ \ce{NO + O2} \label{step 2} \end{align*}\]

Зверніть увагу, що проміжний вид\(\ce{NO3}\) має лише перехідне існування і не фігурує в чистому рівнянні.

Властивості механізму

Корисний механізм реакції

складається з ряду елементарних кроків (визначених нижче), які можуть бути записані як хімічні рівняння, і сума яких дає чисте збалансоване рівняння реакції;
повинні погодитися з законом експериментальної ставки;
рідко, якщо коли-небудь буде доведено абсолютно.

Важливо розуміти, що механізм даної сітчастої реакції може бути різним при різних умовах. Наприклад, дисоціація броміду водню

\[\ce{2 HBr(g) → H2(g) + Br2(g)} \nonumber\]

протікає різними механізмами (і слідує різним законам швидкості) при здійсненні в темряві (термічне розкладання) і на світлі (фотохімічне розкладання). Аналогічно наявність каталізатора може включити альтернативний механізм, який значно прискорює швидкість реакції.

Елементарні кроки

Механізм реакції в кінцевому підсумку слід розуміти як «удар за ударом» опис подій молекулярного рівня, послідовність яких веде від реагентів до продуктів. Ці елементарні кроки (також звані елементарними реакціями) майже завжди дуже прості, що включають один, два або [рідко] три хімічні види, які класифікуються відповідно як

одномолекулярний	\(A →\)	на сьогоднішній день найпоширеніший
бімолекулярний	\(A + B →\)	поширені
термомолекулярний	\(A + B + C →\)	дуже рідко

Елементарні реакції відрізняються від звичайних сітчастих хімічних реакцій двома важливими способами:

Закон швидкості елементарної реакції може бути написаний інспекцією. Наприклад, бімолекулярний процес завжди слідує закону норми другого порядку\(rate=k[A][B]\).
Елементарні кроки часто включають нестабільні або реактивні форми, які не відображаються в рівнянні чистої реакції.

Деякі чисті реакції протікають в один елементарний крок, принаймні за певних умов. Однак без ретельного експериментування ніколи не можна бути впевненим. Газофазоутворення\(\ce{HI}\) з його елементів довго вважалося простим бімолекулярним поєднанням\(\ce{H2}\) і\(\ce{I2}\), але пізніше було встановлено, що за певних умов воно слідує більш складному нормовому закону.

Багатоступінчасті (послідовні) реакції

Дуже поширені механізми, в яких за одним елементарним кроком слідує інший.

\[\ce{ A + B → \cancel{Q} } \tag{step 1}\]

\[\ce{B + \cancel{Q} → C} \tag{step 2}\]

\[\ce{A + 2B → C} \tag{net reaction}\]

(Як завжди має бути, чиста реакція - це лише сума її елементарних кроків.)

У цьому прикладі вид\(Q\) є проміжною, зазвичай нестійкою або високореактивною формою. Якщо обидва кроки протікають з однаковими темпами, експерименти з нормовим законом щодо чистої реакції не виявить, що тут беруть участь два окремі кроки. Закон ставки для реакції був би

\[rate = k[A][B]^2 \nonumber\]

(Майте на увазі, що проміжні продукти, такі як\(Q\) не можуть відображатися в законі швидкості чистої реакції.)

Коли ставки зовсім інші, речі можуть стати цікавими і призвести до досить різноманітної кінетики, а також деяких спрощення наближень. Коли константи швидкості ряду послідовних реакцій досить різні, може вступити в дію ряд взаємозв'язків, які значно спрощують наше розуміння спостережуваної кінетики реакції.

Наближення 1: Крок визначення швидкості наближення

Крок визначення швидкості також відомий як крок обмеження швидкості. Як правило, ми можемо очікувати, що одна з елементарних реакцій у послідовності послідовних кроків матиме постійну швидкості, меншу за інші. Ефект полягає в уповільненні швидкості всіх реакцій - дуже сильно в тому, як лінія автомобілів повільно повзе на пагорб за повільною вантажівкою.

Зображена тут триступінчаста реакція включає два проміжних виду I ₁ і I ₂, і три активованих комплекси під номером X _1-3. Хоча крок I ₂ → продукти має найменшу _{індивідуальну енергію активації Е а} ₃, енергія Х ₃ по відношенню до реагентів визначає енергію активації загальної реакції, позначається крайнім лівим вертикальна стрілка. Таким чином, крок визначення швидкості є

\[X_1 → X_2. \nonumber\]

Хіміки часто називають елементарні реакції, чиї константи швидкості вперед мають великі величини як «швидкі», а ті, у яких постійні швидкості вперед малі, як «повільні». Завжди майте на увазі, однак, що до тих пір, поки кроки тривають в одному файлі (без коротких скорочень!) , Всі вони будуть протікати з однаковою швидкістю. Так що навіть «найшвидші» учасники послідовної серії реакцій будуть протікати так само повільно, як і «найповільніші».

Наближення 2: Швидке наближення рівноваги

У багатьох багатоступінчастих процесах константи прямої і зворотної швидкості для формування проміжного\(Q\) мають аналогічні величини і досить великі, щоб реакція в кожному напрямку була досить швидкою. Розкладання проміжного продукту є більш повільним процесом:

\[\ce{A <=>[k_1][k_{-1}] Q ->[k_2] B} \nonumber\]

Це часто описується як швидке рівновагу, в якому концентрація\(Q\) може бути пов'язана з постійною рівноваги.

\[K = \dfrac{k_1}{k_{–1}} \nonumber\]

Це лише Закон масових дій. Слід розуміти, однак, що справжня рівновага ніколи не досягається, оскільки\(Q\) постійно споживається; тобто швидкість утворення\(Q\) завжди перевищує швидкість його розкладання. З цієї причини стаціонарне наближення, описане нижче, як правило, є кращим для лікування процесів такого роду.

Наближення 3: Стале наближення

Розглянемо механізм, що складається з двох послідовних реакцій.

\[\ce{A ->[k_1] Q ->[k_2] B} \nonumber\]

в якому\(Q\) є проміжним. Профілі часу проти концентрації цих трьох речовин залежатимуть від відносних величин\(k_1\) і\(k_2\), як показано на наступних діаграмах. Побудова цих діаграм вимагає розв'язання множин одночасних диференціальних рівнянь, що [на щастя!] поза рамками цього курсу.

Стаціонарне наближення зазвичай не висвітлюється на вступних курсах, хоча і не відрізняється особливою складністю математично.

На лівій діаграмі крок визначення швидкості явно є перетворенням швидко сформованого проміжного продукту в продукт, тому немає необхідності формулювати закон ставки, який передбачає\(Q\). Але з правого боку, формування\(Q\) є визначальним, але його перетворення в\(B\) настільки швидке, що\([Q]\) ніколи не накопичується до істотної вартості. (Зверніть увагу, як ділянки для\([A]\) і\([B]\) майже взаємно обернені.) Ефект полягає в підтримці концентрації\(Q\) при приблизно постійному значенні. Таке стаціонарне наближення може значно спростити аналіз багатьох механізмів реакції, особливо тих, які опосередковані ферментами в організмах.

Перетворення механізмів у закони ставок

Ми не можемо безпосередньо дивитися на елементарні кроки, приховані в «чорній скриньці» механізму реакції, ми обмежуємося пропозицією послідовності, яка б відповідала порядку реакції, який ми можемо спостерігати. Хімічна інтуїція може направляти нас у цьому, наприклад, вгадуючи величини деяких енергій активації. Зрештою, однак, найкраще, що ми можемо зробити, - це розробити механізм, який є правдоподібним; ми ніколи не можемо «довести», що те, що ми придумали, є фактичним механізмом.

Приклад\(\PageIndex{1A}\): A + B → C

Розглянемо наступну реакцію:

\[A + B → C\nonumber\]

Один з можливих механізмів може включати два проміжні продукти\(Q\) і\(R\):

Крок 1	\(\ce{A + B ->[k_1] Q}\)	(повільний, визначення швидкості)
Крок 2	\(\ce{Q + A ->[k_2] R }\)	(швидко)
Крок 3	\(\ce{ R + B ->[k_3] C }\)	(швидко)

Закон ставки, відповідний цьому механізму, був би кроком визначення ставки:

\[\text{rate} = k_1[A][B]. \nonumber\]

Якщо першим кроком у механізмі є визначення швидкості, легко знайти закон ставки для загального вираження з механізму. Якщо другий або пізніший крок є визначенням ставки, визначення закону ставки трохи складніше і часто вимагає будь-якого з двох наближення вище для ідентифікації.

Приклад\(\PageIndex{1B}\): A + B → C

Альтернативний механізм наступної реакції:

\[A + B → C \nonumber\]

в якому крок визначення швидкості включає в себе один з проміжних продуктів буде відображати кінетику третього порядку:

Крок 1	\(\ce{A + B <=>[k_1][k_{-1}] Q}\)	(Швидка рівновага)
Крок 2	\(\ce{Q + A ->[k_2] R }\)	(повільний, визначення швидкості)
Крок 3	\(\ce{ R + B ->[k_3] C }\)	(швидко)

Оскільки проміжні продукти не можуть з'являтися у виразах закону швидкості, ми повинні\([Q]\) виражати на етапі визначення швидкості з точки зору інших реагентів. Для цього скористаємося тим, що крок 1 передбачає постійну рівноваги\(K_1\):

\[K_1 = \dfrac{k_1}{k_{-1}} = \dfrac{[Q]}{[A][B]} \nonumber\]

Вирішуючи це для\([Q]\), отримуємо

\[[Q] = K_1[A][B]. \nonumber \]

Тепер ми можемо висловити закон ставки для 2 як

\[\begin{align*} \text{rate} &= k_2 K_1[A][B][A] \\[4pt] &= k[A]^2[B] \end{align*}\]

в якому константи\(k_2\) і\(K_1\) були об'єднані в єдину константу\(k\).

Приклад\(\PageIndex{2}\): F₂ + 2 NO₂ → 2 NO₂F

Розглянемо наступну реакцію:

\[\ce{ F2 + 2 NO2 → 2 NO2F }\nonumber\]

Застосування «хімічної інтуїції», згаданої у наведеному вище полі, призведе нас до підозри, що будь-який процес, який передбачає розрив міцного зв'язку F - F, швидше за все, буде досить повільним, щоб обмежити швидкість, і що отримані атомні фтори будуть дуже швидко реагувати з іншими непарними електронними видами:

Крок 1	\(\ce{F2 + 2 NO2 ->[k_1] NO2F + F + NO2}\)	(повільний, визначення швидкості)
Крок 2	\(\ce{F + NO2 ->[k_2] NO2F}\)	(дуже швидко)

Якщо цей механізм правильний, то закон швидкості чистої реакції буде таким, як крок визначення швидкості:

\[\text{rate} = k_1[F_2][NO_2] \nonumber\]

Приклад\(\PageIndex{3}\): Decomposition of ozone

Озон - це нестабільний алотроп кисню, який розкладається назад на звичайний диоксиген відповідно до чистої реакції.

\[\ce{2 O3 → 3 O2} \nonumber\]

Можливим механізмом було б просте одноступінчасте бімолекулярне зіткнення, запропоноване рівнянням реакції, але це призведе до закону швидкості другого порядку, який не спостерігається. Натомість експеримент виявляє більш складний закон ставки:

\[\text{rate} = [O_3]^2[O_2]^{–1} \nonumber\]

Що це? Виглядає так, ніби O ₂ насправді певним чином пригнічує реакцію. Загальноприйнятим механізмом цієї реакції є:

Крок 1	\(\ce{O3 <=>[k_1][k_{-1}] O2+ O}\)	(Швидка рівновага)
Крок 2	\(\ce{O + O3 ->[k_2] 2 O2}\)	(визначення швидкості)

Чи здається це розумним? Зверніть увагу, що

Рівновага на кроці 1 повинна бути досить швидкою, оскільки нестабільність озону прогнозує низьку енергію активації для подальшого процесу. Те ж саме можна сказати і про зворотний процес, який включає високоактивний атом кисню, який, як ми очікуємо, швидко з'їсть одну з незв'язних електронних пар на молекулі O ₂.
Інгібуючий ефект O ₂ можна пояснити ефектом Ле Шательє - будучи продуктом рівноваги в 1, накопичення кисню змушує його назад вліво.
На кроці 2 можна очікувати, що атом O реагує з озоном так само швидко, як це відбувається з O ₂ у зворотному кроці 1, але інші дослідження показують, що це не так. Постійна швидкості k ₂, ймовірно, досить велика. З огляду на сильний ковалентний зв'язок в O ₂, ми не очікуємо значної зворотної реакції.

Щоб перевести цей механізм в закон швидкості, спочатку запишемо постійну рівноваги для кроку 1 і вирішимо її для концентрації проміжного:

\[ K =\dfrac{[O_2][O]}{[O_3]} \nonumber\]

\[[O] = \dfrac{k_1[O_3]}{k_{-1}[O_2]} \nonumber\]

Підставляємо це значення\(\ce{[O]}\) в експресію швидкості\(\ce{[O][O3]}\) для кроку 2, що дає експериментально отриманий закон ставки

\[ rate = k_1K \dfrac{[O_3]^2}{[O_2]} \nonumber\]

Приклад\(\PageIndex{4}\): A reaction having an apparently Negative E_a

Розглянемо газофазне окислення оксиду азоту:

\[\ce{2 NO + O_2 → 2 NO_2} \nonumber\]

Ця реакція, як і більшість реакцій третього порядку, не є термімолекулярною, а скоріше комбінацією рівноваги з подальшим бімолекулярним кроком:

Крок 1	\(\ce{ NO + NO <=>[k_1][k_{-1}] N2O2}\)	(Рівновага, ур. конст. К)
Крок 2	\(\ce{ N2O2 + O2 ->[k_2] 2 NO2}\)	(обмеження швидкості)

Оскільки проміжний\(\ce{N2O2}\) може не з'явитися в рівнянні швидкості, нам потрібно висловити його концентрацію в терміні реагенту\(NO\). Як і в попередньому прикладі, ми робимо це через постійну рівноваги кроку 1:

\[K = \dfrac{[N_2O_2]}{[NO]^2} \nonumber\]

\[[N_2O_2] = K [NO]^2 \nonumber\]

\[ \begin{align*} \text{rate} &= k_2 [N_2O_2 ][O_2] \\[4pt] &= k_2 K [NO]^2 [O_2] \end{align*} \]

Незвичайною особливістю цієї чистої реакції є те, що її швидкість зменшується з підвищенням температури, що говорить про те, що енергія активації негативна. Реакція 1 передбачає утворення зв'язків і носить екзотермічний характер, тому при підвищенні температури\(K\) зменшується (ефект Ле Шательє). При цьому до ₂ збільшується, але недостатньо для подолання зниження\(K\). Так що, мабуть, негативна енергія активації загального процесу є просто артефактом величин протилежних температурних коефіцієнтів k ₂ і\(K\).

Ланцюгові реакції (механізми позитивного зворотного зв'язку)

Багато важливих механізмів реакції, особливо в газовій фазі, включають проміжні продукти, що мають непарні електрони, широко відомі як вільні радикали. Вільні радикали часто досить стабільні термодинамічно і можуть бути досить довгоживучими самі по собі, але вони високореактивні, а отже, кінетично лабільні. Точка ·, що представляє непарний електрон, насправді не є частиною формули і зазвичай відображається лише тоді, коли ми хочемо підкреслити радикальний характер виду. «Атомні» форми багатьох елементів, які зазвичай утворюють двоатомні молекули, є вільними радикалами; H·, O · і Br· є поширеними прикладами. Найпростішим і стабільним (Δ G = +87 кДж/моль) молекулярний вільний радикал або "непарно-електронна молекула" є оксид азоту, NO·.

Найважливішим хімічним властивістю вільного радикала є його здатність передавати непарний електрон разом іншому виду, з яким він реагує. Цей процес поширення ланцюга створює новий радикал, який стає здатним ініціювати іншу реакцію. Радикали, звичайно, також можуть реагувати один з одним, знищуючи обидва («припинення ланцюга»), створюючи при цьому новий вид, пов'язаний з ковалентами.

Макс Боденштейн

Значна частина новаторської роботи в цій галузі, класичним прикладом якої є\(\ce{HBr}\) синтез, була виконана німецьким хіміком Максом Боденштейном (1871-1942)

Синтез броміду водню з його елементів ілюструє основні особливості ланцюгової реакції. Цифри в правій колонці - це енергії активації на моль.

Крок 1	Бар ₂ + М → 2 Бр·	ініціювання ланцюга (Δ Н° = +188 кДж)
Крок 2	Бр· Н ₂ → Н· + ГБр	розмноження ланцюгом (+75 кДж)
Крок 3	Н· + Br ₂ → Гбр + Бр·	Ланцюгове поширення (—176 кДж)
Крок 4	Н· + ГБр → Н ₂ + Бр·	гальмування ланцюга (—75 кДж)
Крок 5	2 Бр· + М → М* + Бр ₂	припинення ланцюга (—188 кДж)

Зверніть увагу на наступні моменти:

Для початку реакції повинен утворитися вільний радикал (1). Якщо температура газу досить висока, то Br· може утворитися від більш енергійних зіткнень молекул Br ₂ з якоюсь іншою молекулою M (швидше за все, другий Br ₂). Це відомо як термічна активація; Іншим способом створення вільних радикалів є фотохімічна активація.
Реакції 2 і 3 споживають вільний радикал, але утворюють інший, таким чином «поширюючи» ланцюг.
У реакції 4 молекула продукту руйнується, тим самим частково не здійснюючи чистий процес.
Якби тільки перші чотири реакції були активними, то цикл продовжувався б нескінченно довго. Але реакція 5 споживає ланцюговий носій Br·, не виробляючи нових радикалів, тим самим припиняючи ланцюг. Функція молекули M полягає в поглинанні деякої кінетичної енергії зіткнення, щоб два атоми брому не просто відскакували. Продукт M* являє собою термічно збуджений M, який швидко розсіює свою енергію іншим молекулам.
Інші реакції, такі як рекомбінація атомів водню, також мають місце, але їх внесок у загальну кінетику зазвичай дуже малий.

Закони швидкості для ланцюгових реакцій, як правило, дуже складні, і часто мають неінтегральні порядки.

Розгалуження ланцюгових реакцій: Вибухи

Газофазове окислення водню широко вивчалося в широкому діапазоні температур і тисків.

\[\ce{H2(g) + 1/2 O2(g) → H2O(g)}\quad ΔH^o = –242\, kJ/mol \nonumber\]

Ця реакція зовсім не відбувається, коли два гази просто змішуються при кімнатній температурі. При температурі близько 500-600°C вона протікає досить плавно, але при нагріванні вище 700° або запаленні іскрою суміш вибухає. Як і у всіх реакцій горіння, механізм цієї реакції вкрай складний (не хочеться бачити закон швидкості!) і дещо змінюється в залежності від умов. Деякі з основних радикальних кроків формування:

Крок 1	Н ₂ + О ₂ → ХО ₂ · + Н ·	ініціювання ланцюга
Крок 2	Н ₂ + ХО ₂ · → ГО· + Н ₂ О	розмноження ланцюга
Крок 3	Н· + О ₂ → О· + О·	розмноження ланцюга +розгалуження
Крок 4	О· + Ч ₂ → О· + Н·	ланцюгове розмноження+розгалуження
Крок 5	О· Н ₂ → Н ₂ О + Н·	поширення ланцюга
Вид HO ₂ · відомий як пергідроксил; HO· є гідроксилом (не плутати з гідроксильним іоном HO: ^-)

Реакції 3 і 4 народжують більше радикалів, ніж вони споживають, тому, коли вони активні, кожен з них ефективно ініціює новий ланцюговий процес, змушуючи загальну швидкість збільшуватися в геометричній прогресії, виробляючи вибух.

Межі вибуху

Вибухонебезпечна реакція - це високоекзотермічний процес, який, як тільки розпочався, йде до завершення дуже швидко і не може бути зупинений. Руйнівна сила вибуху виникає внаслідок швидкого розширення газоподібних продуктів, оскільки вони поглинають тепло реакції. Існує два основних види хімічних вибухів:

Теплові вибухи відбуваються, коли тепло виділяється реакцією швидше, ніж воно може вийти з реакційного простору. Це змушує реакцію протікати швидше, виділяючи ще більше тепла, що призводить до постійно прискорюється швидкості втечі.
Ланцюгові вибухи відбуваються, коли кількість носіїв ланцюга збільшується в геометричній прогресії, ефективно висіваючи в суміш нові реакційні центри. Потім процес перетворюється на тепловий вибух.

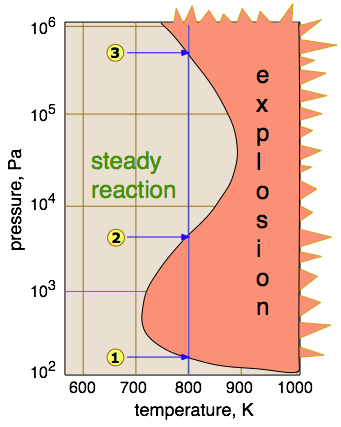
Від того, чи протікає реакція вибухонебезпечно, залежить від балансу між утворенням і знищенням ланцюгоносних видів. Цей баланс залежить від температури і тиску, як показано тут для реакції водень-кисень.

Пряма рекомбінація ланцюгових носіїв зазвичай вимагає зіткнення трьох тіл з іншою молекулою, щоб поглинути частину кінетичної енергії; такі потрійні процеси малоймовірні при дуже низькому тиску. Таким чином, нижче нижньої межі вибуху радикали (включаючи ті, що утворюються іскрою), як правило, здатні досягати стінок контейнера і об'єднуватися там - або у випадку вибуху на відкритому повітрі просто поєднуються з іншими молекулами, коли вони виходять з активного об'єму реакції.
У зоні вибуху між і (які для більшості газів відомі як нижня - і верхня межі вибуху) процеси поширення і розгалуження працюють ефективно і вибухонебезпечно, навіть коли суміш нагрівається однорідно.
Вище концентрація молекул газу достатня, щоб дозволити потрійні зіткнення, які дозволяють процесам припинення ланцюга ефективно працювати, тим самим пригнічуючи розгалуження. Вище цієї верхньої межі реакції за участю більшості газів протікають плавно.
Водень незвичайний тим, що він демонструє третю межу вибуху. Причиною цього було щось загадкове протягом деякого часу, але зараз вважається, що вибухи в цій області не передбачають розгалуження, а термічно індуковані реакцією
HO ₂ · + H ₂ → H ₂ O ₂ + H·.

Нижня межа вибуху газових сумішей змінюється залежно від розміру, форми та складу огороджувальної ємності. Само собою зрозуміло, що експериментальне визначення меж вибуху вимагає певної уважності та творчості. Верхня і нижня межі вибуху для декількох загальних паливних газів наведені нижче.