16.4: Рівняння Нернста
- Page ID
- 19204
Переконайтеся, що ви добре розумієте наступні основні ідеї. Особливо важливо, щоб ви знали точні значення всіх виділених термінів в контексті даної теми.
- Рівняння Нернста пов'язує ефективні концентрації (активності) компонентів клітинної реакції зі стандартним потенціалом клітини. Для простого зменшення форми M n + ne — → M це говорить про те, що потенціал півкомірки зміниться на 59/ n мВ за 10-кратну зміну активності іона.
- Іонні концентрації зазвичай можуть використовуватися замість діяльності, коли загальна концентрація іонів в розчині не перевищує приблизно 0,001 М.
- У тих реакціях, в яких беруть участь H + або OH — іони, потенціал клітини також буде залежати від рН. Графіки Е проти рН, що показують області стабільності споріднених видів, є дуже корисним засобом узагальнення окислювально-відновної хімії елемента.
Стандартні потенціали клітин, про які ми говорили в попередньому розділі, відносяться до клітин, в яких всі розчинені речовини знаходяться в одиничній активності, що по суті означає «ефективну концентрацію» 1 М. Аналогічно, будь-які гази, які беруть участь в реакції електрода, знаходяться на ефективний тиск (відомий як fugacity) 1 атм. Якщо ці концентрації або тиск мають інші значення, потенціал клітини зміниться таким чином, який можна передбачити з принципів, які ви вже знаєте.
Потенціали клітин залежать від концентрацій
Припустимо, наприклад, що ми зменшуємо концентрацію\(Zn^{2+}\) в\(Zn/Cu\) осередку від її стандартного ефективного значення 1 М до набагато меншого значення:
\[Zn(s) | Zn^{2+}(aq, 0.001\,M) || Cu^{2+}(aq) | Cu(s)\]
Це зменшить значення\(Q\) для реакції клітини
\[Zn(s) + Cu^{2+} → Zn^{2+} + Cu(s)\]
тим самим роблячи його більш спонтанним, або «рухаючи його праворуч», як передбачав би принцип Ле Шательє, і робить його вільну енергетичну зміну\(\Delta G\) більш негативною\(\Delta G°\), ніж, так що це\(E\) було б більш позитивним, ніж\(E^°\). Співвідношення між фактичним потенціалом клітини\(E\) і стандартним потенціалом\(E^°\) розробляється наступним чином. Почнемо з виведеного раніше рівняння, яке пов'язує стандартну зміну вільної енергії (для повного перетворення продуктів в реагенти) до стандартного потенціалу
\[\Delta G° = –nFE° \]
За аналогією можна записати більш загальне рівняння
\[\Delta G = –nFE\]
який виражає зміну вільної енергії для будь-якої міри reaction— тобто для будь-якого значення коефіцієнта реакції\(Q\). Тепер ми підставляємо їх у вираз, який стосується\(\Delta G\) і\(\Delta G°\) який ви згадаєте з глави про хімічну рівновагу:
\[\Delta G = \Delta G° + RT \ln Q\]
який дає
\[–nFE = –nFE° + RT \ln Q \]
які можна переставити на
\[ \color{red} {\underbrace{E=E° -\dfrac{RT}{nF} \ln Q}_{\text{applicable at all temperatures}}} \label{Nernst Long}\]
Це рівняння Нернста, яке пов'язує потенціал клітини зі стандартним потенціалом і з діяльністю електроактивних видів. Зверніть увагу, що потенціал клітини буде таким же, як\(E°\) тільки якщо\(Q\) це єдність. Рівняння Нернста частіше записується у формі журналу base-10 і для 25° C:
\[ \color{red} {\underbrace{E=E° -\dfrac{0.059}{n} \log_{10} Q}_{\text{Applicable at only 298K}}} \label{Nernst Short}\]
Значення рівняння Нернста
Рівняння Нернста говорить нам, що потенціал напівкомірки зміниться на 59 мілівольт за 10-кратну зміну концентрації речовини, що бере участь в окисленні або відновленні на один електрон; для двоелектронних процесів варіація становитиме 28 мілівольт за десятиліття зміни концентрації. Таким чином, для розчинення металевої міді
\[Cu_{(s)} \rightarrow Cu^{2+} + 2e^–\]
потенціал
\[E = (– 0.337) – 0.0295 \log_{10} [Cu^{2+}]\]
стає більш позитивним (реакція має більшу тенденцію до протікання) у міру зменшення концентрації іонів міді. Це, звичайно, саме те, що передбачає принцип Le Chatelier; чим більше розбавлений продукт, тим більша ступінь реакції.

Електроди з врівноваженістю
Рівняння трохи вище для напівосередку Cu/Cu 2 + викликає цікаве питання: припустимо, ви занурюєте шматок міді в розчин чистої води. При Q = [Cu 2 +] = 0 різниця потенціалів між електродом і розчином повинна бути нескінченною! Вам загрожує удар електричним струмом? Вам не потрібно турбуватися; без будь-якої передачі електронів, немає заряду, щоб зап вас з. Звичайно, це буде не дуже довго, перш ніж деякі іони Cu 2 + з'являться в розчині, і якщо таких іонів на літр всього кілька, потенціал зменшується лише до 20 вольт. Більш того, система настільки далека від рівноваги (наприклад, не вистачає іонів для заповнення електричного подвійного шару), що рівняння Нернста насправді не дає значущих результатів. Такий електрод, як кажуть, не працює. Яка іонна концентрація потрібна для врівноваження електрода? Я насправді не знаю, але я б з підозрою ставився до чогось набагато нижче 10 —6 М.
Іони протилежного заряду мають тенденцію асоціюватися в нещільно зв'язані іонні пари в більш концентрованих розчині, тим самим зменшуючи кількість іонів, які вільні дарувати або приймати електрони на електроді. З цієї причини рівняння Нернста не може точно передбачити потенціали напівкомірок для розчинів, в яких загальна іонна концентрація перевищує приблизно 10 —3 М.

Як насправді потенціал клітини залежить від концентрації! Рівняння Нернста точно прогнозує потенціали клітин тільки тоді, коли рівноважний частний член Q виражається в діяльності. Іонна активність все більше відходить від концентрацій, коли останні перевищують від 10 -4 до 10 —5 М, залежно від розмірів і зарядів іонів.
Якщо рівняння Нернста застосовується до більш концентрованих розчинів, терміни в коефіцієнті реакції Q повинні бути виражені в «ефективних концентраціях» або активності електроактивних іонних видів. Коефіцієнт активності\(\gamma\)) пов'язує концентрацію іона з його активністю (а) в даному розчині через відношення.
\[a = \gamma c\]
Оскільки електродні потенціали вимірюють діяльність безпосередньо, коефіцієнти активності можна визначити шляхом проведення відповідних вимірювань ЕРС на комірках, в яких відома концентрація цікавить іона. Отримані Es потім можуть бути використані для перетворення концентрацій в діяльність для використання в інших розрахунках, що включають константи рівноваги.
Потенціали клітин і рН: діаграми стійкості
Як більшість з нас згадує з нашої боротьби з балансуванням окислювально-відновних рівнянь на початкових курсах хімії, багато реакцій перенесення електронів включають іони водню та гідроксидні іони. Тому стандартні потенціали для цих реакцій відносяться до рН, або 0, або 14, при якому відповідний іон має одиничну активність. Оскільки часто беруть участь декілька чисел іонів H + або OH, потенціали, задані рівнянням Нернста, можуть сильно відрізнятися залежно від рН. Часто корисно поглянути на ситуацію по-іншому, розглядаючи, які комбінації потенціалу і рН дозволяють стабільно існувати той чи інший вид. Ця інформація найбільш корисним чином виражається за допомогою E -vs. -pH діаграма, також відома як діаграма Пурбе.
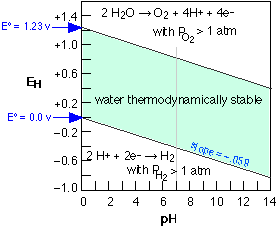
Як було зазначено у зв'язку з затіненою областю на малюнку нижче, вода піддається розкладанню сильними окислювачами, такими як Cl 2, і відновниками сильніше H 2. Реакцію редукції можна записати як
\[2H^+ + 2e^– \rightarrow H_{2}(g) \]
або, в нейтральних або лужних розчинами як
\[2H_2O + 2 e^– \rightarrow H_{2}(g) + 2 OH^–\]
Ці дві реакції еквівалентні і слідують одному і тому ж рівнянню Нернста.
\[E_{H^+/H_2} = E_{H^+/H_2}^o + \dfrac{RT}{nF} \ln \left( \dfrac{[H^+]^2} {P_{H_2}} \right)\]
який при 25°С і одиниці Н 2 парціальний тиск знижується до
\[E = E° - \dfrac{0.059}{2} × 2 pH = –0.059\; pH\]
Аналогічно відбувається окислення води
\[2H_2O \rightarrow O_{2}(g) + 4 H^+ + 2 e^–\]
регулюється рівнянням Нернста
\[ E_{O_2/H_2O} = E_{O_2/H_2O}^o + \dfrac{RT}{nF} \ln \left( P_{O_2}[H^+]^4 \right)\]
який аналогічно стає E = 1,23 - 0,059 рН, тому графіки E-vs -pH для обох процесів мають однакові схили і дають діаграму стійкості для води на рис\(\PageIndex{2}\). Ця діаграма Пурбе має особливе значення для електрохімічної корозії металів. Таким чином, метали вище водню в ряді активності будуть схильні до окислення (корозії) шляхом зменшення іонів H + або води.
Оскільки хлор широко використовується як дезінфікуючий засіб для питної води, басейнів та очищення стічних вод, варто подивитися на його діаграму стійкості. Зверніть увагу, що ефективним бактерицидним засобом є не сам Cl 2, а його продукт окислення хлорноватиста кислота HoCl, яка переважає при значеннях рН нижче її pK a 7,3. Зауважте також, що
- Cl 2 нестійкий у воді, за винятком дуже низького рН; він розкладається на HoCl і Cl —.
- Хлорноватиста кислота та її аніон є сильнішими окислювачами, ніж O 2 і, таким чином, піддаються розкладанню у воді. Єдиним стабільним видом хлору у воді є Cl -.
- Розпад HoCl відбувається дуже повільно в темний час доби, але каталізується сонячним світлом. З цієї причини хлор у зовнішніх басейнів повинен часто оновлюватися.
- Розпад Cl 2 і HoCl шляхом реакції з органічним матеріалом в комунальних системах водопостачання іноді змушує вводити додатковий хлор у віддалених місцях.
Кожна суцільна лінія являє собою комбінацію Е та рН, при якій два види по обидва боки від неї можуть співіснувати; у всіх інших точках стабільний лише один вид. Зверніть увагу, що рівноваги між видами, розділеними діагональними лініями, залежать як від E, так і від рН, тоді як ті, що розділені горизонтальними або вертикальними лініями, впливають лише на рН або лише E відповідно.
Діаграми стабільності здатні конденсувати велику кількість інформації в компактне уявлення і широко використовуються в геохімії та корозійної інженерії. Діаграма Пурбе для заліза - один з найбільш часто зустрічаються прикладів.
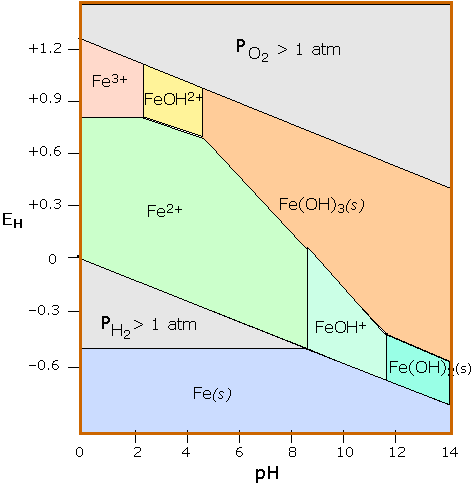
Схема Пурбе для праски. На цій діаграмі представлені три ступеня окислення заліза (0, +2 і +3). Області стійкості для станів окисленого заліза показані лише в області стабільності H 2 O. Рівноваги між видами, розділеними вертикальними лініями, залежать лише від рН.
Стан окислення +3 є єдиним стабільним в середовищах, в яких рівень окислення контролюється атмосферним O 2. Саме тому земна кора містить оксиди заліза, які розвинулися тільки після появи зелених рослин, які є джерелом O 2. Залізо піддається нападу H + з утворенням H 2 і Fe (II); останній потім реагує з O 2, утворюючи різні кольорові оксиди Fe (III), які складають «іржу». Численні інші види, такі як оксиди та водні оксиди, не показані. Дійсно «повна» діаграма для заліза повинна мати принаймні два додаткові розміри, що показують парціальний тиск O 2 і CO 2.
Концентрація клітин
З вашого дослідження термодинаміки ви можете згадати, що процес
розчинений (концентрований) → розчинений (розбавлений)
супроводжується падінням вільної енергії, а тому здатний виконувати роботу над оточенням; все, що потрібно - це якийсь практичний спосіб захоплення цієї роботи. Один із способів зробити це за допомогою концентраційної клітини, такої як
Кубок (и) | КуНО (3,1 м) || КуНО (3,01 М) | Кубку (и)
катод: Cu 2 + (.1 М) + 2 е — → Cu (s)
анод: Cu (s) → Cu 2 + (0,01 М) + 2 е —
Далі: Куб 2 + (0,1 М) → Куб 2 + (0,01 М)
що представляє транспорт іона міді з області більш високої концентрації до однієї з меншою концентрацією.
Рушійною силою цього процесу є зміна вільної енергії ΔG, пов'язана з градієнтом концентрації (C 2 - C 1), іноді відома як вільна енергія розведення:
\[ΔG_{dilution} = RT \ln(C_2 – C_1)\]
Зверніть увагу, однак, що іони Cu 2+ не повинні фізично переміщатися між двома відсіками; потік електронів через зовнішній ланцюг створює «віртуальний» потік, оскільки іони міді створюються в стороні низької концентрації і розряджаються на протилежному електроді. Нітратні іони також повинні проходити між клітинами для підтримки електронейтральності. Рівняння Нернста для цієї комірки дорівнює
\[E = E^° - \left(\dfrac{0.059}{n}\right) \log_{10} Q = 0 - 0.29 \log_{10} 0.1 = +0.285 \,V\]
Зверніть увагу, що\(E^°\) для концентраційної клітини завжди дорівнює нулю, оскільки це буде потенціал клітини, в якій електроактивні види знаходяться в одиничній активності в обох відділеннях.
\(E^°\)для концентраційної осередку завжди дорівнює нулю,
