Skip to main content
LibreTexts - Ukrayinska

6.4: Газові закони

  1. Last updated
  2. Save as PDF
  • Page ID
    22670

    • Anonymous
    • LibreTexts
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Дізнайтеся, що мається на увазі під терміном газові закони.
    • Вивчіть і застосовуйте закон Бойла.
    • Вивчайте і застосовуйте закон Чарльза.

    Коли вчені XVII століття почали вивчати фізичні властивості газів, вони помітили деякі прості зв'язки між деякими вимірними властивостями газу. Візьмемо, наприклад, тиск (P) і обсяг (V). Вчені відзначили, що для заданої кількості газу (зазвичай виражається в одиницях молів [n]), якщо температура (T) газу підтримувалася постійною, тиск і об'єм були пов'язані: При збільшенні одного зменшується інший. У міру зменшення одного збільшується інший. Ми говоримо, що тиск і обсяг обернено пов'язані між собою.

    Однак є більше: тиск і обсяг заданої кількості газу при постійній температурі чисельно пов'язані. Якщо взяти величину тиску і помножити його на величину об'єму, то твір є постійною для заданої кількості газу при постійній температурі:

    P × V = постійна при постійних n і T

    Якщо або обсяг або тиск змінюються, поки кількість і температура залишаються однаковими, то інша властивість повинна змінюватися так, щоб продукт двох властивостей все одно дорівнював тій самій константі. Тобто, якщо початкові умови маркуються P 1 і V 1 і нові умови маркуються P 2 і V 2, ми маємо

    Р 1 В 1 = постійна = Р 2 В 2

    де припускається, що властивості множаться разом. Залишивши середню частину, ми просто

    Р 1 V 1 = P 2 V 2 при постійній n і Т

    Це рівняння є прикладом газового закону. Закон газу - це проста математична формула, яка дозволяє моделювати або прогнозувати поведінку газу. Цей конкретний газовий закон називається законом Бойла, на честь англійського вченого Роберта Бойла, який вперше оголосив його в 1662 році. \(\PageIndex{1}\)На малюнку показано два уявлення про те, як працює закон Бойла.

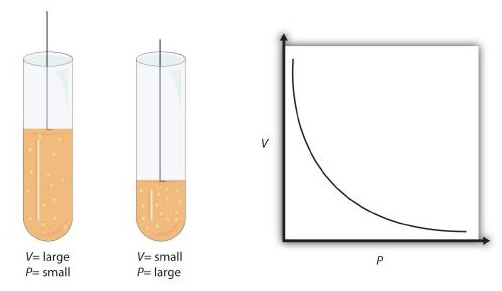
    2 пробірки з різною кількістю рідин (зліва) та графічна діаграма з нахилом вниз (праворуч).
    Ілюстрація\(\PageIndex{1}\): Закон Бойля. Поршень, що має певний тиск і об'єм (лівий поршень), матиме половину обсягу, коли його тиск буде вдвічі більше (правий поршень). Також можна побудувати графік P проти V для заданої кількості газу при певній температурі; така ділянка буде виглядати як графік праворуч.

    Закон Бойла є прикладом другого типу математичної задачі, яку ми бачимо в хімії - на основі математичної формули. Тактика роботи з математичними формулами відрізняється від тактики роботи з коефіцієнтами перерахунку. По-перше, більшість питань, на які вам доведеться відповісти за допомогою формул, є питаннями типу слів, тому перший крок - визначити, які величини відомі, і призначити їх змінним. По-друге, у більшості формул деякі математичні перестановки (тобто алгебра) повинні бути виконані для розв'язання невідомої змінної. Правило полягає в тому, що для знаходження значення невідомої змінної необхідно математично ізолювати невідому змінну сама по собі і в чисельнику однієї сторони рівняння. Нарешті, одиниці повинні бути послідовними. Наприклад, в законі Бойла є дві змінні тиску; вони повинні мати однакову одиницю. Є також дві змінні томи; вони також повинні мати однакову одиницю. У більшості випадків не має значення, що таке одиниця, але одиниця повинна бути однаковою з обох сторін рівняння.

    Приклад\(\PageIndex{1}\)

    Пробка газу має початковий тиск 2,44 атм і початковий обсяг 4,01 л. Його тиск змінюється до 1,93 атм. Який новий обсяг, якщо температура і кількість підтримуються постійними?

    Рішення

    Для початку визначаємо, які величини нам дані. Нам дано початковий тиск і початковий обсяг, тому нехай ці значення будуть P 1 і V 1:

    Р 1 = 2,44 атм і V 1 = 4,01 л

    Нам дається ще одна величина, кінцевий тиск 1,93 атм, але не кінцевий обсяг. Цей кінцевий обсяг є змінною, для якої ми будемо вирішувати.

    Р 2 = 1,93 атм і V 2 =? Л

    Підставивши ці значення в закон Бойла, отримуємо

    (2,44 атм) (4,01 л) = (1,93 атм) V 2

    Для розв'язання невідомої змінної виділимо її, діливши обидві сторони рівняння на 1,93 атм — як число, так і одиницю:

    \[\frac{(2.44\, atm)(4.01\, L)}{1.93\, atm}=\frac{(1.93\, atm)\, V_{2}}{1.93\, atm}\nonumber \]

    Зверніть увагу, що в лівій частині рівняння одиниця атм знаходиться в чисельнику і знаменнику дробу. Вони скасовують алгебраїчно, так само, як і число. З правого боку одиниця атм і число 1.93 знаходяться в чисельнику і знаменнику, тому вся кількість скасовується:

    \[\frac{(2.44\, \cancel{atm})(4.01\, L)}{1.93\, \cancel{atm}}=\frac{(1.93\, \cancel{atm})\, V_{2}}{1.93\, \cancel{atm}}\nonumber \]

    Те, що у нас залишилося

    \[\frac{(2.44)(4.01\, L)}{1.93}=V_{2}\nonumber \]

    Тепер просто множимо і ділимо числа разом і поєднуємо відповідь з\(L\) одиницею, яка є одиницею обсягу. Роблячи так, отримуємо\(V_2 = 5.07\, L\)

    Чи має сенс ця відповідь? Ми знаємо, що тиск і об'єм обернено пов'язані між собою; коли одне зменшується, інше збільшується. Тиск знижується (з 2,44 атм до 1,93 атм), тому обсяг повинен збільшуватися, щоб компенсувати, і він становить (від 4,01 л до 5,07 л). Тож відповідь має сенс, заснований на законі Бойла.

    Вправа\(\PageIndex{1}\)

    Якщо Р 1 = 334 торр, В 1 = 37,8 мл, а Р 2 = 102 торр, що таке V 2?

    Відповідь

    124 мл

    Як уже згадувалося, ви можете використовувати будь-які одиниці для тиску або обсягу, але обидва тиску повинні бути виражені в однакових одиницях, і обидва об'єми повинні бути виражені в однакових одиницях.

    Приклад\(\PageIndex{2}\)

    Проба газу має початковий тиск 722 торр і початковий об'єм 88,8 мл. Його обсяг змінюється до 0,663 л. Що таке новий тиск?

    Рішення

    Ми все ще можемо використовувати закон Бойла, щоб відповісти на це, але тепер дві об'ємні величини мають різні одиниці. Не має значення, яку одиницю ми змінюємо, доки ми виконуємо перетворення правильно. Змінимо 0,663 л на мілілітри:

    \[0.663\, L\times \frac{1000\, ml}{1\, L}=663\, ml\nonumber \]

    Тепер, коли обидві об'ємні величини мають однакові одиниці, ми можемо замінити закон Бойла:

    \[(722\, torr)(88.8\, ml)=P_{2}(663\, ml)\nonumber \]

    \[\frac{(722\, torr)(88.8)\, ml}{(663\, ml)}=P_{2}\nonumber \]

    Одиниці mL скасовуємо, а множимо і ділимо числа, щоб отримати P 2 = 96,7 торр

    Обсяг збільшується, а тиск знижується, що, як очікується за законом Бойла.

    Вправа\(\PageIndex{2}\)

    Якщо V 1 = 456 мл, Р 1 = 308 торр, а Р 2 = 1,55 атм, що таке V 2?

    Відповідь

    119 мл

    Існують і інші вимірні характеристики газу. Однією з них є температура (Т). Можливо, можна варіювати температуру проби газу і відзначити, який вплив вона надає на інші властивості газу. Ранні вчені зробили саме це, виявивши, що якщо кількість газу і його тиск підтримуються постійними, то зміна температури змінює обсяг (V). Зі збільшенням температури обсяг збільшується; при зниженні температури обсяг зменшується. Ми говоримо, що ці дві характеристики безпосередньо пов'язані між собою.

    Математична залежність між V і T повинна бути можливою, за винятком однієї думки: яку температурну шкалу ми повинні використовувати? З глави 2 ми знаємо, що наука використовує кілька можливих температурних шкал. Експерименти показують, що обсяг газу пов'язаний з його абсолютною температурою в Кельвіні, а не його температурою в градусах Цельсія. Якщо температура газу виражається в кельвінів, то експерименти показують, що відношення обсягу до температури є постійною:

    \[\frac{V}{T}=constant\nonumber \]

    Ми можемо модифікувати це рівняння, коли ми модифікували закон Бойла: початкові умови V 1 і T 1 мають певне значення, і значення повинно бути однаковим, коли умови газу змінюються на деякі нові умови V. 2 і Т 2, до тих пір, поки тиск і кількість газу залишаються постійними. Таким чином, у нас є ще один газовий закон:

    \[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\; at\; constant\; P\; and\; n\nonumber \]

    Цей газовий закон прийнято називати законом Шарля, після французького вченого Жака Шарля, який проводив експерименти над газами в 1780-х роках. Тактика використання цієї математичної формули аналогічна таким для закону Бойла. Для визначення невідомої величини використовуйте алгебру для виділення невідомої змінної сама по собі і в чисельнику; одиниці подібних змінних повинні бути однаковими. Але додамо ще одну тактику: всі температури повинні бути виражені в абсолютній температурній шкалі (Кельвін). Нагадаємо, ми переглядаємо перетворення між шкалою абсолютної температури та шкалою температури Цельсія:

    К = °C + 273

    де K позначає температуру в кельвінів, а °C - температуру в градусах Цельсія.

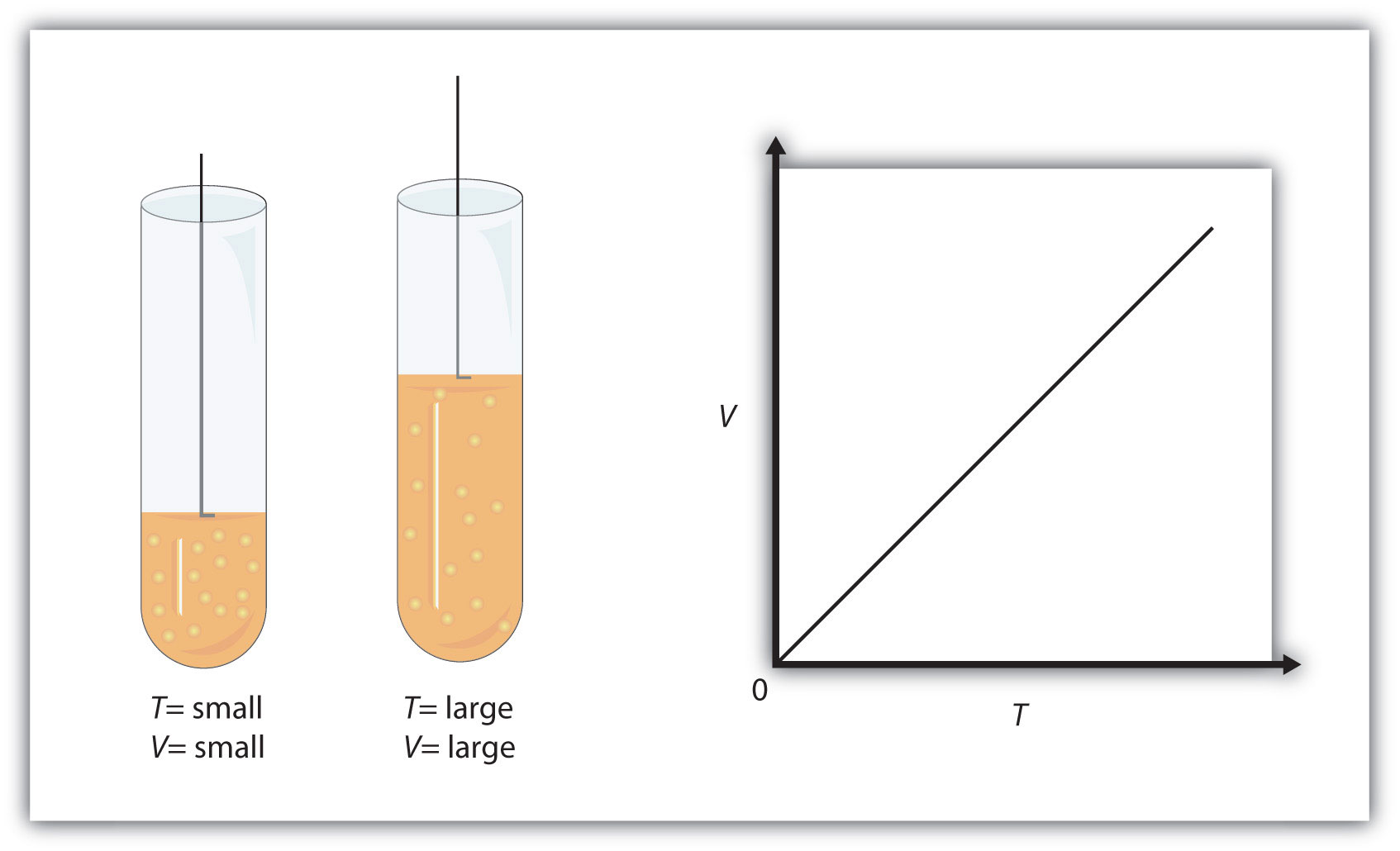
    2 пробірки з різною кількістю рідин (зліва) та графічна діаграма з нахилом вгору (праворуч).
    Малюнок (\ pageIndex {2}\): Закон Чарльза. Поршень, що має певний обсяг і температуру (лівий поршень), буде мати в два рази більше обсягу, коли його температура в два рази більше (правий поршень). Можна також побудувати V проти T для заданої кількості газу при певному тиску; така ділянка буде виглядати як графік праворуч.
    Приклад\(\PageIndex{3}\)

    Проба газу має початковий об'єм 34,8 мл і початкову температуру 315 К. Який новий обсяг, якщо температура підвищена до 559 К? Припустимо постійний тиск і кількість для газу.

    Рішення

    Спочатку ми присвоюємо задані значення їх змінним. Початковий обсяг V 1, тому V 1 = 34,8 мл, а початкова температура T 1, тому T 1 = 315 К. Температура підвищена до 559 К, тому кінцева температура T 2 = 559 К. Відзначимо, що температури вже наведені в кельвінів, тому нам не потрібно перетворювати температури. Підставляючи в вираз закон Чарльза поступається

    \[\frac{34.8\, ml}{315\, K}=\frac{V_{2}}{559\, K}\nonumber \]

    Вирішуємо для V 2 шляхом алгебраїчного виділення змінної V 2 на одній стороні рівняння. Робимо це шляхом множення обох сторін рівняння на 559 К (число і одиниця). Коли ми це робимо, блок температури скасовується з лівого боку, тоді як весь 559 К скасовується з правого боку:

    \[\frac{(559\cancel{K})(34.8\, ml)}{315\, \cancel{K}}=\frac{V_{2}(\cancel{559\, K})}{\cancel{559\, K}}\nonumber \]

    Вираз спрощує

    \[\frac{(559)(34.8\, ml)}{315}=V_{2}\nonumber \]

    Помножуючи і діливши числа, ми бачимо, що єдина одиниця, що залишилася - mL, тому наша остаточна відповідь

    V 2 = 61,8 мл

    Чи має сенс ця відповідь? Ми знаємо, що зі збільшенням температури обсяг збільшується. Тут температура зростає з 315 К до 559 К, тому гучність теж повинна збільшуватися, що вона і робить.

    Вправа\(\PageIndex{3}\)

    Якщо V 1 = 3,77 Л і Т 1 = 255 К, що таке V 2, якщо Т 2 = 123 К?

    Відповідь

    1.82 Л

    Математично складніше, якщо кінцева температура повинна бути розрахована, оскільки змінна T знаходиться в знаменнику закону Чарльза. Існує кілька математичних способів роботи з цим, але, мабуть, найпростіший спосіб - прийняти взаємний закон Карла. Тобто, замість того, щоб писати його як

    \[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\nonumber \]

    записати рівняння як

    \[\frac{T_{1}}{V_{1}}=\frac{T_{2}}{V_{2}}\nonumber \]

    Це все ще рівність і правильна форма закону Чарльза, але тепер змінна температури знаходиться в чисельнику, а алгебра, необхідна для прогнозування кінцевої температури, простіше.

    Приклад\(\PageIndex{4}\)

    Пробка газу має початковий об'єм 34,8 л і початкову температуру −67°С Якою має бути температура газу, щоб його об'єм становив 25,0 л?

    Рішення

    Тут ми шукаємо кінцеву температуру, тому будемо використовувати зворотну форму закону Чарльза. Однак початкова температура задається в градусах Цельсія, а не кельвінів. Ми повинні перетворити початкову температуру в кельвіни:

    −67°C +273 = 206 К

    Використовуючи закон газу, ми повинні використовувати T 1 = 206 K в якості температури. Підставивши у відповідну форму закон Карла, отримуємо

    \[\frac{206\, K}{34.8\, L}=\frac{T_{2}}{25.0\, L}\nonumber \]

    Перевівши величину 25,0 л на іншу сторону рівняння, отримаємо

    \[\frac{(25.0\cancel{L})(206\, K)}{34.8\cancel{L}}=T_{2}\nonumber \]

    L одиниці скасовують, тому наша остаточна відповідь T 2 = 148 K

    Це також дорівнює −125°C. Зі зменшенням температури обсяг зменшується, як це робиться в цьому прикладі.

    Вправа\(\PageIndex{4}\)

    Якщо V 1 = 623 мл, T 1 = 255° C, а V 2 = 277 мл, що таке T 2?

    Відповідь

    235 К, або −38°C

    Резюме

    • Поведінка газів можна моделювати газовими законами.
    • Закон Бойла стосується тиску та обсягу газу при постійній температурі та кількості.
    • Закон Чарльза стосується обсягу та температури газу при постійному тиску та кількості.
    • У газових законі температури завжди повинні виражатися в кельвінів.