8.10: Закон про ідеальний газ
- Page ID
- 21980
Цілі навчання
- Використовувати ідеальний закон газу для опису поведінки газу.
In a gas, molecules freely move, filling any volume that they occupy. The kinetic energy of the molecules greatly exceeds any potential energy of attraction or repulsion between molecules and the size of the molecules are miniscule compared to the average space between them. Contrast this with solids, where the molecules are held in place by the attractive forces and the comparatively small kinetic energy only results in the molecules jiggling in place when thermally excited. Again, in a solid, the molecules are packed so closely together that the volume of the solid is essentially that of the sum of the molecular volumes of all of the molecules in it. Liquids represent a situation where molecular attraction and kinetic energy are balanced and the spacing between molecules is higher than in solids but much less than in gases.
At high temperatures and low pressures, where the kinetic energy and the spacing between molecules are both large, one may neglect both the miniscule attractive forces and molecular volume. Under such conditions the properties of the gas, the pressure, P, volume, V, number of moles, n, and the temperature, T are independent of the mixture of molecules in the gas. In that limit the behavior of the gas is called ideal, and governed by the ideal gas law
No gases are truly ideal, but while no model is perfect, some are useful, and under most commonly encountered conditions, the ideal gas law is very useful indeed to describe the behavior of gases. It is also easy to predict that the conditions where the ideal gas law would have trouble describing the behavior of a gas would be low temperature (small molecular kinetic energy) and high pressure (little space between molecules). The behavior of gases under such conditions becomes increasingly like that of liquids and will be discussed in the next chapter.
The Ideal Gas Law
The ideal gas law
\( PV = nRT \tag{10.3.1} \)
relates the pressure, volume, temperature and number of moles in a gas to each other. R is a constant called the gas constant. The ideal gas law is what is called an equation of state because it is a complete description of the gas's thermodynamic state. No other information is needed to calculate any other thermodynamic variable, and, since the equation relates four variables, a knowledge of any three of them is sufficient.
Pressure, volume and number of moles, the latter sometime called extent, share an important property, they can never be negative. What would a negative volume be, or an absolute negative pressure or extent? The concepts do not even exist. This means that temperature in the ideal gas law is similarly limited. It can never be negative.
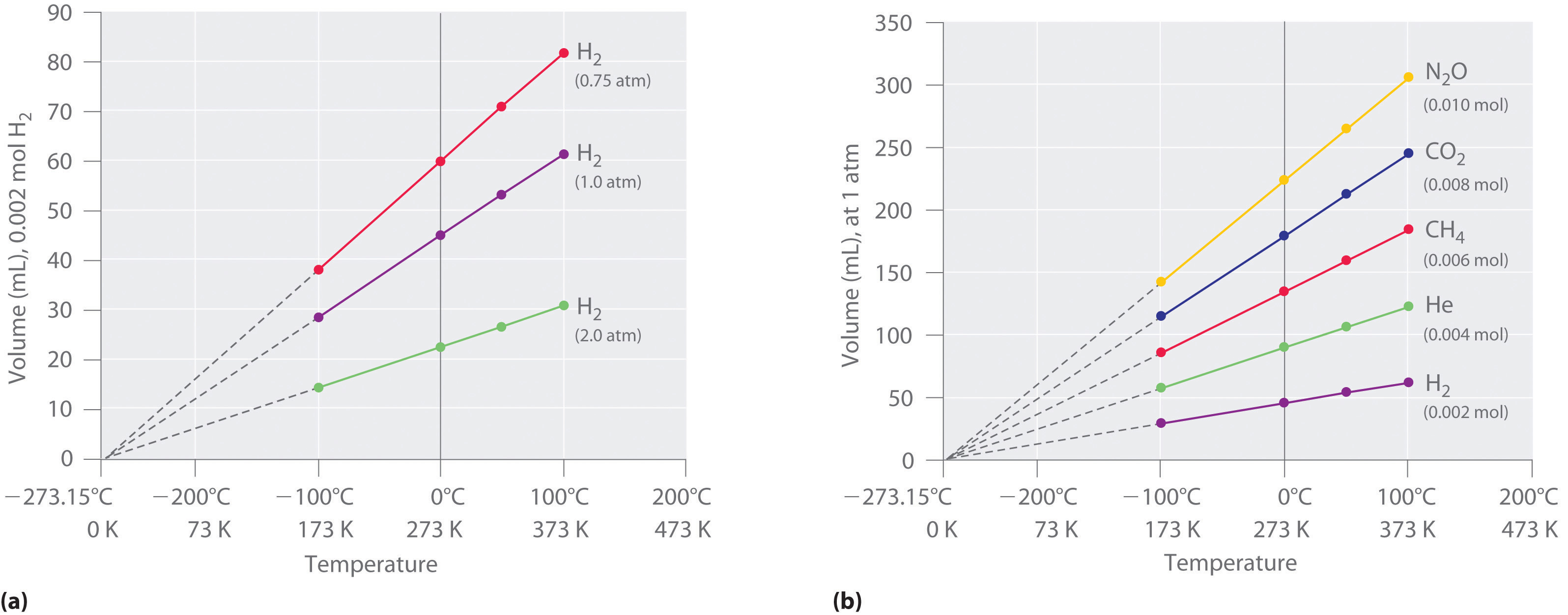
We can determine what zero temperature on the ideal gas scale is by holding the number of moles and the pressure constant and extrapolate the temperature measured in Celcius to what its value would be at zero volume
Figure 10.3.1 The Relationship between Volume and Temperature (a) In these plots of volume versus temperature for equal-sized samples of H2 at three different pressures, the solid lines show the experimentally measured data down to −100°C, and the broken lines show the extrapolation of the data to V = 0. The temperature scale is given in both degrees Celsius and Kelvin. Although the slopes of the lines decrease with increasing pressure, all of the lines extrapolate to the same temperature at V = 0 (−273.15°C = 0 K). (b) In these plots of volume versus temperature for different amounts of selected gases at 1 atm pressure, all the plots extrapolate to a value of V = 0 at −273.15°C, regardless of the identity or the amount of the gas.
The extrapolated temperature corresponding to zero volume at constant pressure and amount is -273.15 °C, which is called absolute zero because no lower temperature is possible (unless, of course you can come up with a negative volumes, but you cannot). For convenience we set the degrees on the Kelvin scale to the size of the degree on the Celcius scale. In other words
\( 1 \; K = 1 ^{o}C \tag{10.3.2} \)
Note the Pattern
Before we can use the ideal gas law, however, we need to know the value of the gas constant R. Its form depends on the units used for the other quantities in the expression. If V is expressed in liters (L), P in atmospheres (atm), T in kelvins (K), and n in moles (mol), then
\( R = 0.08206 \;L \cdot atm /\left (K\cdot ·mol \right ) \tag{10.3.3} \)
Because the product PV has the units of energy, as described in Section 8.1 and Essential Skills 4 (Section 9.9), R can also have units of J/(K·mol) or cal/(K·mol):
\( R = 8.3145 \;J/\left (K \cdot mol \right ) = 1.9872 cal/\left (K \cdot mol \right )
\tag{10.3.4} \)
Scientists have chosen a particular set of conditions to use as a reference: 0°C (273.15 K) and 1 atm pressure, referred to as standard temperature and pressure (STP) The conditions 0°C (273.15 K) and 1 atm pressure for a gas.
This can be confusing because as discussed in the previous chapter,the standard state for enthalpies of reaction and formation is 298K. Be sure to use the appropriate standard state for enthalpies (298 K) and gas problems (273.15 K)
We can calculate the volume of 1.000 mol of an ideal gas under standard conditions using the variant of the ideal gas law given in Equation 10.3.1:
\( V = \dfrac{nRT}{P}= \dfrac{\left (1.000 \; \cancel{mol} \left ( 0.082057 \; L\cdot \cancel{atm}/\cancel{K}\cdot \cancel{mol} \right )\right )\left ( 273.15 \; \cancel{K} \right )}{1.000\; \cancel{atm}}=22.31\; L \tag{10.3.5} \)
Thus the volume of 1 mol of an ideal gas at 0°C and 1 atm pressure is 22.41 L, approximately equivalent to the volume of three basketballs. The quantity 22.41 L is called the standard molar volumeThe volume of 1 mol of an ideal gas at STP (0°C and 1 atm pressure), which is 22.41 L. of an ideal gas. The molar volumes of several real gases at STP are given in Table 10.3.1, which shows that the deviations from ideal gas behavior are quite small. Thus the ideal gas law does a good job of approximating the behavior of real gases at STP.
Table 10.3.1 Molar Volumes of Selected Gases at Standard Temperature (0°C) and Pressure (1 atm)
| Gas | Molar Volume (L) |
|---|---|
| He | 22.434 |
| Ar | 22.397 |
| H2 | 22.433 |
| N2 | 22.402 |
| O2 | 22.397 |
| CO2 | 22.260 |
| NH3 | 22.079 |
Applying the Ideal Gas Law
The ideal gas law allows us to calculate the value of the fourth variable for a gaseous sample if we know the values of any three of the four variables (P, V, T, and n). It also allows us to predict the final state of a sample of a gas (i.e., its final temperature, pressure, volume, and amount) following any changes in conditions if the parameters (P, V, T, and n) are specified for an initial state. Some applications are illustrated in the following examples. The approach used throughout is always to start with the same equation—the ideal gas law—and then determine which quantities are given and which need to be calculated. Let’s begin with simple cases in which we are given three of the four parameters needed for a complete physical description of a gaseous sample.
Example 10.3.1
The balloon that Charles used for hisflight in 1783 was destroyed, but we can estimate that its volume was 31,150 L (1100 ft3), given the dimensions recorded at the time. If the temperature at ground level was 86°F (30°C) and the atmospheric pressure was 745 mmHg, how many moles of hydrogen gas were needed to fill the balloon?
Given: volume, temperature, and pressure
Asked for: amount of gas
Strategy:
A Solve the ideal gas law for the unknown quantity, in this case n.
B Make sure that all quantities are given in units that are compatible with the units of the gas constant. If necessary, convert them to the appropriate units, insert them into the equation you have derived, and then calculate the number of moles of hydrogen gas needed.
Solution:
A We are given values for P, T, and V and asked to calculate n. If we solve the ideal gas law (Equation 10.3.1) for n, we obtain
\( n = \dfrac{PV}{RT} \)
B P and T are given in units that are not compatible with the units of the gas constant [R = 0.082057 (L·atm)/(K·mol)]. We must therefore convert the temperature to kelvins and the pressure to atmospheres:
\[\rm745\; \cancel{mmHg} \times\dfrac{1\;atm}{760\; \cancel{mmHg}}=0.980\;atm\]
\[T=273+30=303{\rm K}\]
Substituting these values into the expression we derived for n, we obtain
\[n=\dfrac{PV}{RT}=\rm\dfrac{0.980\; \cancel{atm} \times31150\; \cancel{L} }{0.08206\dfrac{\cancel{atm} \cdot \cancel{L} }{\rm mol\cdot \cancel{K}}\times 303\; \cancel{K}}=1.23\times10^3\;mol\]
Exercise
Suppose that an “empty” aerosol spray-paint can has a volume of 0.406 L and contains 0.025 mol of a propellant gas such as CO2. What is the pressure of the gas at 25°C?
Answer: 1.5 atm
In Example 5, we were given three of the four parameters needed to describe a gas under a particular set of conditions, and we were asked to calculate the fourth. We can also use the ideal gas law to calculate the effect of changes in any of the specified conditions on any of the other parameters, as shown in Example 6.
Using the Ideal Gas Law to Calculate Gas Densities and Molar Masses
The ideal gas law can also be used to calculate molar masses of gases from experimentally measured gas densities. To see how this is possible, we first rearrange the ideal gas law to obtain
\[\dfrac{n}{V}=\dfrac{P}{RT}\tag{10.3.6}\]
The left side has the units of moles per unit volume (mol/L). The number of moles of a substance equals its mass (m, in grams) divided by its molar mass (M, in grams per mole):
\[n=\dfrac{m}{M}\tag{10.3.7}\]
Substituting this expression for n into Equation 10.4.12 gives
\[\dfrac{m}{MV}=\dfrac{P}{RT}\tag{10.3.8}\]
Because m/V is the density d of a substance, we can replace m/V by d and rearrange to give
\[ d=\dfrac{m}{V}=\dfrac{MP}{RT}\tag{10.3.9} \]
The distance between particles in gases is large compared to the size of the particles, so their densities are much lower than the densities of liquids and solids. Consequently, gas density is usually measured in grams per liter (g/L) rather than grams per milliliter (g/mL).
Example 10.3.2
Calculate the density of butane at 25°C and a pressure of 750 mmHg.
Given: compound, temperature, and pressure
Asked for: density
Strategy:
A Calculate the molar mass of butane and convert all quantities to appropriate units for the value of the gas constant.
B Substitute these values into Equation 10.3.9 to obtain the density.
Solution:
A The molar mass of butane (C4H10) is
\( (4)(12.011) + (10)(1.0079) = 58.123 \; g/mol \notag \)
Using 0.082057 (L·atm)/(K·mol) for R means that we need to convert the temperature from degrees Celsius to kelvins (T = 25 + 273 = 298 K) and the pressure from millimeters of mercury to atmospheres:
\[P=\rm750\;mmHg\times\dfrac{1\;atm}{760\;mmHg}=0.987\;atm \notag \]
B Substituting these values into Equation 10.3.9 gives
\[d=\rm\dfrac{58.123\;g/mol\times0.987\;atm}{0.08206\dfrac{L\cdot atm}{K\cdot mol}\times298\;K}=2.35\;g/L \notag \]
Exercise
Radon (Rn) is a radioactive gas formed by the decay of naturally occurring uranium in rocks such as granite. It tends to collect in the basements of houses and poses a significant health risk if present in indoor air. Many states now require that houses be tested for radon before they are sold. Calculate the density of radon at 1.00 atm pressure and 20°C and compare it with the density of nitrogen gas, which constitutes 80% of the atmosphere, under the same conditions to see why radon is found in basements rather than in attics.
Answer: radon, 9.23 g/L; N2, 1.17 g/L
A common use of Equation 10.3.9 is to determine the molar mass of an unknown gas by measuring its density at a known temperature and pressure. This method is particularly useful in identifying a gas that has been produced in a reaction, and it is not difficult to carry out. A flask or glass bulb of known volume is carefully dried, evacuated, sealed, and weighed empty. It is then filled with a sample of a gas at a known temperature and pressure and re-weighed. The difference in mass between the two readings is the mass of the gas. The volume of the flask is usually determined by weighing the flask when empty and when filled with a liquid of known density such as water. The use of density measurements to calculate molar masses is illustrated in Example 10.
Example 10.3.3
The reaction of a copper penny with nitric acid results in the formation of a red-brown gaseous compound containing nitrogen and oxygen. A sample of the gas at a pressure of 727 mmHg and a temperature of 18°C weighs 0.289 g in a flask with a volume of 157.0 mL. Calculate the molar mass of the gas and suggest a reasonable chemical formula for the compound.
Given: pressure, temperature, mass, and volume
Asked for: molar mass and chemical formula
Strategy:
A Solve Equation 10.3.8 for the molar mass of the gas and then calculate the density of the gas from the information given.
B Convert all known quantities to the appropriate units for the gas constant being used. Substitute the known values into your equation and solve for the molar mass.
C Propose a reasonable empirical formula using the atomic masses of nitrogen and oxygen and the calculated molar mass of the gas.
Solution:
A Solving Equation 10.3.8 for the molar mass gives
\[M=\dfrac{mRT}{PV}=\dfrac{dRT}{P} \notag \]
Density is the mass of the gas divided by its volume:
\[d=\dfrac{m}{V}=\dfrac{0.289\rm g}{0.17\rm L}=1.84 \rm g/L \notag \]
B We must convert the other quantities to the appropriate units before inserting them into the equation:
\[T=18+273=291 K \notag \]
\[P=727\rm mmHg\times\dfrac{1\rm atm}{760\rm mmHg}=0.957\rm atm \notag \]
The molar mass of the unknown gas is thus
\[d=\rm\dfrac{1.84\;g/L\times0.08206\dfrac{L\cdot atm}{K\cdot mol}\times291\;K}{0.957\;atm}=45.9 g/mol \notag \]
C The atomic masses of N and O are approximately 14 and 16, respectively, so we can construct a list showing the masses of possible combinations:
\[M({\rm NO})=14 + 16=30 \rm\; g/mol \notag \]
\[M({\rm N_2O})=(2)(14)+16=44 \rm\;g/mol \notag \]
\[M({\rm NO_2})=14+(2)(16)=46 \rm\;g/mol \notag \]
The most likely choice is NO2 which is in agreement with the data. The red-brown color of smog also results from the presence of NO2 gas.
Exercise
You are in charge of interpreting the data from an unmanned space probe that has just landed on Venus and sent back a report on its atmosphere. The data are as follows: pressure, 90 atm; temperature, 557°C; density, 58 g/L. The major constituent of the atmosphere (>95%) is carbon. Calculate the molar mass of the major gas present and identify it.
Answer: 44 g/mol; CO2
Summary
The empirical relationships among the volume, the temperature, the pressure, and the amount of a gas can be combined into the ideal gas law, PV = nRT. The proportionality constant, R, is called the gas constant and has the value 0.08206 (L·atm)/(K·mol), 8.3145 J/(K·mol), or 1.9872 cal/(K·mol), depending on the units used. The ideal gas law describes the behavior of an ideal gas, a hypothetical substance whose behavior can be explained quantitatively by the ideal gas law and the kinetic molecular theory of gases. Standard temperature and pressure (STP) is 0°C and 1 atm. The volume of 1 mol of an ideal gas at STP is 22.41 L, the standard molar volume. All of the empirical gas relationships are special cases of the ideal gas law in which two of the four parameters are held constant. The ideal gas law allows us to calculate the value of the fourth quantity (P, V, T, or n) needed to describe a gaseous sample when the others are known and also predict the value of these quantities following a change in conditions if the original conditions (values of P, V, T, and n) are known. The ideal gas law can also be used to calculate the density of a gas if its molar mass is known or, conversely, the molar mass of an unknown gas sample if its density is measured.
Key Takeaway
- The ideal gas law is derived from empirical relationships among the pressure, the volume, the temperature, and the number of moles of a gas; it can be used to calculate any of the four properties if the other three are known.
Key Equations
Ideal gas law
Equation 10.3.1: \( PV = nRT \)
where \(R = 0.08206 \dfrac{\rm L\cdot atm}{\rm K\cdot mol}=8.3145 \dfrac{\rm J}{\rm K\cdot mol}\)
Density of a gas
Equation 10.3.9: \(d=\dfrac{MP}{RT}\)
Conceptual Problems
-
For an ideal gas, is volume directly proportional or inversely proportional to temperature? What is the volume of an ideal gas at absolute zero?
-
What is meant by STP? If a gas is at STP, what further information is required to completely describe the state of the gas?
-
Given the following initial and final values, what additional information is needed to solve the problem using the ideal gas law?
Given Solve for V1, T1, T2, n1 n 2 P1, P2, T2, n2 n 1 T1, T2 V 2 P1, n1 P 2 -
Given the following information and using the ideal gas law, what equation would you use to solve the problem?
Given Solve for P1, P2, T1 T 2 V1, n1, n2 V 2 T1, T2, V1, V2, n2 n 1 -
Using the ideal gas law as a starting point, derive the relationship between the density of a gas and its molar mass. Which would you expect to be denser—nitrogen or oxygen? Why does radon gas accumulate in basements and mine shafts?
-
Use the ideal gas law to derive an equation that relates the remaining variables for a sample of an ideal gas if the following are held constant.
- amount and volume
- pressure and amount
- temperature and volume
- temperature and amount
- pressure and temperature
-
Tennis balls that are made for Denver, Colorado, feel soft and do not bounce well at lower altitudes. Use the ideal gas law to explain this observation. Will a tennis ball designed to be used at sea level be harder or softer and bounce better or worse at higher altitudes?
Answer
-
- P/T = constant
- V/T = constant (Charles’ law)
- P/n = constant
- PV = constant (Boyle’s law)
- V/n = constant (Avogadro’s law)
Numerical Problems
-
Calculate the number of moles in each sample at STP.
- 1580 mL of NO2
- 847 cm3 of HCl
- 4.792 L of H2
- a 15.0 cm × 6.7 cm × 7.5 cm container of ethane
-
Calculate the number of moles in each sample at STP.
- 2200 cm3 of CO2
- 1200 cm3 of N2
- 3800 mL of SO2
- 13.75 L of NH3
-
Calculate the mass of each sample at STP.
- 36 mL of HI
- 550 L of H2S
- 1380 cm3 of CH4
-
Calculate the mass of each sample at STP.
- 3.2 L of N2O
- 65 cm3 of Cl2
- 3600 mL of HBr
-
Calculate the volume in liters of each sample at STP.
- 1.68 g of Kr
- 2.97 kg of propane (C3H8)
- 0.643 mg of (CH3)2O
-
Calculate the volume in liters of each sample at STP.
- 3.2 g of Xe
- 465 mg of CS2
- 5.34 kg of acetylene (C2H2)
-
Calculate the volume of each gas at STP.
- 1.7 L at 28°C and 96.4 kPa
- 38.0 mL at 17°C and 103.4 torr
- 650 mL at −15°C and 723 mmHg
-
Calculate the volume of each gas at STP.
- 2.30 L at 23°C and 740 mmHg
- 320 mL at 13°C and 97.2 kPa
- 100.5 mL at 35°C and 1.4 atm
-
One method for preparing hydrogen gas is to pass HCl gas over hot aluminum; the other product of the reaction is AlCl3. If you wanted to use this reaction to fill a balloon with a volume of 28,500 L at sea level and a temperature of 78°F, what mass of aluminum would you need? What volume of HCl at STP would you need?
-
An 3.50 g sample of acetylene is burned in excess oxygen according to the following reaction:
2 C2H2(g) + 5 O2(g) → 4 CO2(g) + 2 H2O(l)At STP, what volume of CO2(g) is produced?
-
Calculate the density of ethylene (C2H4) under each set of conditions.
- 7.8 g at 0.89 atm and 26°C
- 6.3 mol at 102.6 kPa and 38°C
- 9.8 g at 3.1 atm and −45°C
-
Determine the density of O2 under each set of conditions.
- 42 g at 1.1 atm and 25°C
- 0.87 mol at 820 mmHg and 45°C
- 16.7 g at 2.4 atm and 67°C
-
At 140°C, the pressure of a diatomic gas in a 3.0 L flask is 635 kPa. The mass of the gas is 88.7 g. What is the most likely identity of the gas?
-
What volume must a balloon have to hold 6.20 kg of H2 for an ascent from sea level to an elevation of 20,320 ft, where the temperature is −37°C and the pressure is 369 mmHg?
-
What must be the volume of a balloon that can hold 313.0 g of helium gas and ascend from sea level to an elevation of 1.5 km, where the temperature is 10.0°C and the pressure is 635.4 mmHg?
-
The average respiratory rate for adult humans is 20 breaths per minute. If each breath has a volume of 310 mL of air at 20°C and 0.997 atm, how many moles of air does a person inhale each day? If the density of air is 1.19 kg/m3, what is the average molecular mass of air?
Answers
-
- 7.05 × 10−2 mol
- 3.78 × 10−2 mol
- 0.2138 mol
- 3.4 × 10−2 mol
-
- 0.21 g HI;
- 840 g H2S;
- 0.988 g CH4
-
- 0.449 L Kr
- 1510 L C3H8
- 3.13 × 10−4 L (CH3)2O
-
- 1.5 L
- 4.87 mL
- 650 mL
-
281 mmHg
-
- 1.0 g/L
- 1.1 g/L
- 4.6 g/L
-
2174