7.6: Співвідношення обсяг-сума

Малюнок$\PageIndex{1}$ ілюструє вплив кількості газу на обсяг. Додавання більшої кількості молекул газу збільшує частоту зіткнення молекул зі стінками, збільшуючи тиск газу. Газ розширюється для зниження тиску до тих пір, поки тиск газу в камері не буде дорівнює зовнішньому тиску.

Малюнок$\PageIndex{1}$: При додаванні більшого газу обсяг газу збільшується, тобто V ₁ /n ₁ = V ₂ /n ₂. Джерело: Науково-дослідний центр Гленна НАСА/Громадське надбання.

Закон Авогадро

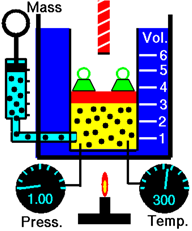
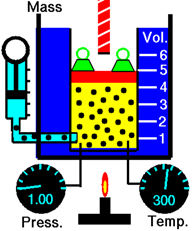
Закон Авогадро стверджує, що обсяг газу прямо пропорційний кількості газу в молі за умови, що температура і тиск газу не змінюються.

Математичні форми закону Авогадро наступні.

$$V\propto {n}\nonumber$$

або

$$V=\mathrm{k}n\nonumber$$

або

$$\dfrac{V}{n}=\mathrm{k}\nonumber$$

де$V$ - обсяг,$n$ - кількість молів, і$k$ є постійною для газу в умовах постійної температури і тиску. Оскільки$\mathrm{V} / \mathrm{n}$ є постійною, вона має на увазі, що:

$$\dfrac{V_{1}}{n_{1}}=\dfrac{V_{2}}{n_{2}}=\mathrm{k}\nonumber$$

де$V_{1}$ і$n_{1}$ є початковим об'ємом і початковим обсягом газу, відповідно і$V_{2}$ і$n_{2}$ є кінцевий обсяг і кінцева кількість газу в моль, за умови, що температура і тиск не змінюються.

Приклад$\PageIndex{1}$

Погодний балон, що містить$3.0$ родимки гелію, має обсяг$66 \mathrm{~L}$. Який кінцевий обсяг, якщо в нього додають$2.0$ родимки гелію. Тиск і температура газу не змінюються?

Рішення

Враховується$\quad V_{1}=66 L, \quad n_{1}=3.0 \mathrm{~mol}, \quad V_{2}=?, \quad n_{2}=3.0+2.0=5.0 \mathrm{~mol}$

Формула:

$$\dfrac{V_{1}}{n_{1}}=\dfrac{V_{2}}{n_{2}}, \nonumber$$

переставити формулу для виділення потрібної змінної:

$$V_{2}=\dfrac{V_{1} n_{2}}{n_{1}}. \nonumber$$

Підключіть значення і розрахуйте:

$$V_{2}=\dfrac{66 \mathrm{~L} \times \times 5.0 \mathrm{~mol}}{3.0 \mathrm{~mol}}=110 \mathrm{~L}. \nonumber$$