11: Броунівський рух

Last updated
Save as PDF

Page ID: 17937

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Броунівський рух відноситься до випадкових рухів дрібних частинок при тепловому збудженні в розчині, вперше описаному Робертом Брауном (1827), ¹, який за допомогою свого мікроскопа спостерігав випадковий, хвилюючий просторовий рух пилкових зерен у воді. Це явище нерозривно пов'язане з дифузією. Дифузія - це макроскопічна реалізація броунівського руху молекул в межах градієнтів концентрації. Теоретична основа цього зв'язку була описана Ейнштейном в 1905 році, ² і Жан Перрен ³ надав докладні експерименти, які підтвердили його прогнози.
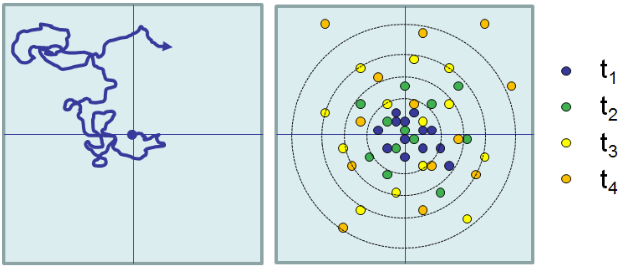
Оскільки рух будь-якої однієї частинки є унікальним, броунівський рух необхідно описати статистично. Ми спостерігаємо, що середньоквадратичне зміщення частинки, усереднене за багатьма вимірами, зростає лінійно з часом, як і при дифузії.

Коефіцієнт пропорційності між середньоквадратичним зміщенням та часом є константою дифузії у другому законі Фіка. Що стосується дифузії, то коефіцієнт пропорційності залежить від розмірності. У 1D, якщо\(\langle x^2(t) \rangle /t = 2D \) потім в 3D\( \langle r^2(t) \rangle /t = 6D \), де D - константа дифузії.

Броунівський рух - властивість молекул при тепловій рівновазі. Це стосується більшої частинки (тобто білка), яка відчуває дисбаланс багатьох мікроскопічних сил, що чиниться багатьма набагато дрібними молекулами оточення (тобто води). Теплове перемішування виникає шляхом поділу кінетичної енергії системи в середньому як k _B T/2 на ступінь свободи. Вільна дифузія має на увазі рух, який обмежується лише кінетичною енергією.

Броунівський рух застосовується до певного діапазону сил і мас, де теплова енергія (k _B T (300 K) = 4,1 пН нм) може мати значний вплив на частинку. Давайте розглянемо середню поступальну кінетичну енергію:

\( \left< \dfrac{mv_x^2}{2} \right> = \dfrac{1}{2}k_BT \)

Для білка ~10 кДа з масою ~10 ^—23 кг середня швидкість кореня в квадраті за рахунок теплової енергії становить\(v_{rms} = \langle v_x^2 \rangle^{1/2}\) = 20 м/с Для води при 300 К, D ~10 ^—5 см ² /с. той же білок має чистий зсув за одну секунду\(x_{rms}=\langle x^2 \rangle ^{1/2}=\sqrt{2Dt} \approx 50 \, \mu \text{m}\). Велика різниця в цих значеннях вказує на велику кількість рандомізуючих зіткнень, які ця частинка відчуває протягом однієї секунди еволюції: (v _rms\(\cdot\) 1sec) /x _rms ≈ 4×10 ⁵. Для білка швидкості і переміщення є домінуючою силою в молекулярній шкалі. Для порівняння, 1 кг маса з k _B T енергії матиме v _rms ~ 10 ^—11 м/с, і не менш незначне зміщення!

Ергодична гіпотеза

Система відома як ергодична, коли середні за часом та середні показники ансамблю для змінної, залежної від часу, рівні.

\[ \begin{aligned} \text{Ensemble average: } &\langle x \rangle = \dfrac{1}{N} \sum_i x_i = \int P(x)x \, dx \\ \text{Time-average: } &\overline{x(t)} = \lim_{T \rightarrow \infty} \dfrac{1}{T} \int^T_0 x(t) dt \end{aligned} \]

На практиці середнє за часом можна обчислити за траєкторією однієї частинки шляхом усереднення по зміщенню, що спостерігається для всіх часових інтервалів в межах траєкторії таким чином, що t= (t _final ‒ t _{початковий}).

У разі броунівського руху та дифузії:\( \left< |r(t) -r_0|^2 \right> = \overline{|r(t)-r_0|^2}\).

11.1: Випадкова прогулянка та дифузія
11.2: Ланцюг Маркова та стохастичні процеси
11.3: Флуоресцентна кореляційна спектроскопія
Флуоресцентна кореляційна спектроскопія (ФКС) дозволяє вимірювати дифузійні властивості флуоресцентних молекул і тісно пов'язана з FRAP. Замість вимірювання залежних від часу профілів концентрації та моделювання кінетики як дифузії континууму, FCS слідує коливанням сталого стану щільності чисел дуже розбавленої молекули флуоресцентного зонда в малому об'ємі, що спостерігається в конфокальному мікроскопі.
11.4: Орієнтаційна дифузія

___________________________________

Браун, «Про частинки, що містяться в пилку рослин; і про загальне існування активних молекул в органічних і неорганічних тілах» у Різні ботанічні праці Роберта Брауна, під редакцією Дж. Беннетта (R. Hardwick, Лондон, 1866), Vol. 1, pp. 463-486.
А. Ейнштейн, Über die фон дер молекулярної кінетичної теорії Wärme geforderte Bewegung фон в Рухенден Flüssigkeiten Підвіска Teilchen, Енн. Фіз.322, 549—560 (1905).
Дж. Перрін, Броунівський рух і молекулярна реальність. (Тейлор і Френсіс, Лондон, 1910).