9.2: Черв'ячний ланцюг

Черв'ячний ланцюг (WLC) - це, мабуть, найбільш часто зустрічаються моделі полімерного ланцюга при описі механіки і термодинаміки макромолекул. Ця модель описує поведінку тонкого гнучкого стрижня і особливо корисна для опису жорстких ланцюгів зі слабкою кривизною, таких як подвійна багатониткова ДНК. Його поведінка залежить тільки від двох параметрів, які описують стрижень:$\kappa_b$ його жорсткість на вигин і$L_C$, довжина контуру.

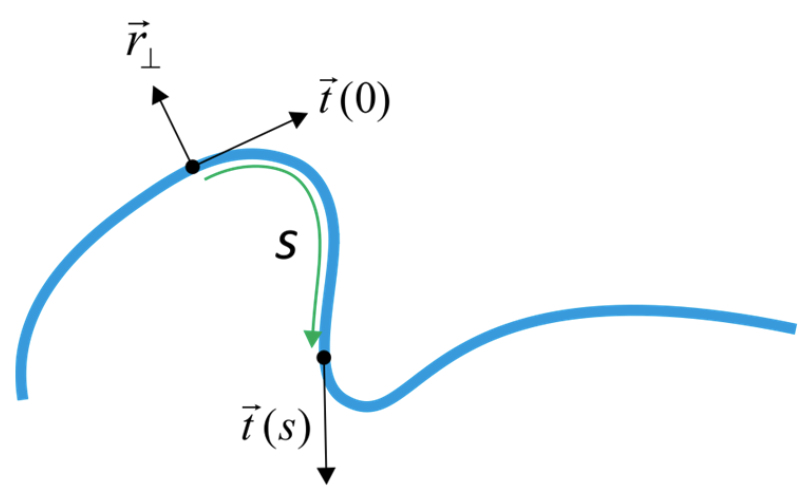
Давайте визначимо змінні в цій моделі WLC:

• $s \qquad \quad \, \text{The distance separating two points along the contour of the rod}$
• $\vec{r}_{\perp} \qquad \, \, \, \text{Normal unit vector}$
• $\vec{t} = \dfrac{\partial \vec{r}_{\perp}}{\partial s} \, \text{Tangent vector}$
• $\dfrac{\partial \vec{t}}{\partial s} \qquad \, \, \text{ Curvature of chain}$
• $\quad =\dfrac{1}{R} \quad \text{is inverse of local radius of curvature}$

Черв'ячатий ланцюг характеризується:

• Довжина стійкості, яка визначається через тангенс векторної кореляційної функції:

$$g(s) = \langle \vec{t}(0) \cdot \vec{t}(s) \rangle = \exp [-|s|/\ell_p] \label{9.2.1}$$

• Енергія вигину: Енергія, необхідна для згинання дотичних векторів сегмента довжини s, може бути виражена як

$$U_b = \dfrac{1}{2} \kappa_b \int^L_0 ds \left( \dfrac{\partial \vec{t}}{\partial s} \right)^2$$

Енергія згинання

Оцінимо енергію вигину WLC, зробивши деякі спрощують припущення, корисні для досить жорстких стрижнів. Якщо розглядати короткі відстані, на яких кривизна невелика, то$\theta \approx s/R$ і

$$\dfrac{\partial \vec{t}}{\partial s} \approx \dfrac{d \theta}{ds} = \dfrac{1}{R} \label{9.2.3}$$

Тоді ми можемо висловити енергію вигину через кут:

$$U_b \approx \dfrac{1}{2s} \kappa_b \theta^2$$

Зверніть увагу на схожість цього виразу з енергією, необхідною для витіснення частинки, пов'язаної в гармонійний потенціал з постійною сили k: U = ½kx ². Енергія вигину може бути використана для отримання термодинамічних середніх. Наприклад, ми можемо обчислити дисперсію для кутів тангенса вектора як функція s (сферичні координати):

$$\begin{align} \langle \theta^2(s) \rangle &= \dfrac{1}{Q_{bend}} \int^{2\pi}_0 d \phi \int^{\pi}_0 d\theta \, \sin \theta \, \theta^2 \, e^{-U_b(\theta )/k_BT} \\ &= \dfrac{2sk_BT}{\kappa_b} \end{align}$$

Ось ми і скористалися$sin θ ≈ θ$. Функція перегородки при згинанні стрижня - це:

$$Q_{bend} = \int^{2\pi}_0 d \phi \int^{\pi}_0 d\theta \, \sin \theta \, e^{-U_b(\theta)/k_BT} \nonumber$$

Стійкість Довжина

Щоб описати довжину стійкості WLC, ми визнаємо, що Equation\ ref {9.2.1} можна записати як$g(s) = \langle \cos \theta (s) \rangle$ і розширити це для малого$θ$:

$$\begin{align*} g(s) &= \langle \cos \theta (s) \rangle \\[4pt] &= \langle 1 - \dfrac{\theta^2 (s)}{2} +... \rangle \\[4pt] &\approx 1 - \dfrac{1}{2} \langle \theta^2(s) \rangle \end{align*}$$

і з Рівняння\ ref {9.2.3} ми можемо записати:

$$g(s) \approx 1-\dfrac{sk_BT}{\kappa_b} \nonumber$$

Якщо порівняти це з розширенням експоненціальної в рівнянні\ ref {9.2.1}

$$g(s) = e^{-|s|/\ell_p} \approx 1-\dfrac{|s|}{\ell_p} \nonumber$$

отримуємо вираз для довжини стійкості черв'ячного ланцюга

$$\ell_p = \dfrac{\kappa_b}{k_BT} \nonumber$$

Відстань від кінця до кінця

Наскрізна відстань для WLC отримується шляхом інтеграції вектора тангенса по одній довжині контуру:

$$\vec{R} = \int^{L_C}_{0} ds \, \vec{t} (s) \nonumber$$

Отже, дисперсія в наскрізній відстані визначається з тангенсної векторної автокореляційної функції, яку ми приймаємо, щоб мати експоненціальну форму:

$$\begin{aligned} \langle R^2 \rangle &= \langle R \cdot R\rangle \\ &= \int^{L_C}_0 ds \int^{L_C}_0 ds' \langle t(s)t(s') \rangle \\ &= \int^{L_C}_0 ds \int ^{L_C}_{0} ds' \, e^{-(s-s')/\ell_p} \end{aligned}$$

$$\langle R^2 \rangle = 2\ell_p L_C - 2\ell_p^2 \left( 1-e^{-L_C/\ell_p} \right) \nonumber$$

Розглянемо цей вираз в двох межах:

$\text{rigid:}\quad \qquad \ell_p \gg L_C \qquad \langle R^2 \rangle \approx L_C^2$

$\text{flexible:} \qquad \ell_p \ll L_C \qquad \langle R^2 \rangle \approx 2L_C \ell_p \rightarrow n_e \ell_e^2 \rightarrow \therefore 2\ell_p = \ell_e$

Приклад$\PageIndex{1}$: DNA Bending in Nucleosomes

Яка енергія потрібна для обгортання ДНК навколо октамера гістону в нуклеосомі? Дволанцюгова ДНК - це жорсткий полімер з довжиною персистенції$\ell_p \approx 50$ нм, але нуклеосома має радіус ~ 4,5 нм.

Рішення

З$\ell_p$ і k _B T = 4,1 пН нм визначити жорсткість на вигин можна за допомогою:

$\kappa_b = \ell_p k_BT = (50\text{ nm})(4.1 \text{ pN nm}) = 205\text{ pN nm}^2$

Тоді енергія, необхідна для згинання dsDNA в один повний цикл

$$\begin{aligned} U_b &\cong \dfrac{\kappa_b \theta^2}{2s} \approx \dfrac{\kappa_b (2\pi)^2}{2(2\pi R)} = \dfrac{\pi \kappa_b}{R} \\ &= \dfrac{\pi(205 \text{ pn nm}^2 )}{4.5 \text{ nm}} = 143 \text{ pN nm} \\ &= 35k_BT = 15 \text{ kcal (mol loops)}^{-1} \\ &\qquad \text{or } 0.15 \text{ kcal basepair}^{-1} \end{aligned}$$

Механіка континууму тонкого стрижня ¹

Черв'ячний ланцюг - це модель, отримана з механіки континууму тонкого стрижня. Крім вигину, тонкий стрижень схильний до інших спотворень: розтягування, скручування, написання.

Підіб'ємо підсумки енергій, необхідних для цих деформацій:

Змінні деформації:

• S: Положення уздовж контуру стрижня
• L ₀: Незбурена довжина стрижня
• $\vec{t}$: Дотичний вектор.
• $d\vec{t}/ds$: викривлення
• Ω: Місцевий поворот

Енергія для спотворення стрижня дорівнює

$$U = U_{st} +U_b+U_{tw} \nonumber$$

У гармонійному наближенні для відновлювальної сили ми можемо записати ці внески як

$$U= \dfrac{1}{2} \int^L_{L_0} \kappa_{st} s ds \, + \dfrac{1}{2} \int^L_{L_0} \kappa_b \left( \dfrac{d\vec{t}}{ds} \right)^2 ds + \dfrac{1}{2} \int^L_{L_0} \kappa_{tw} \Omega^2 ds \nonumber$$

Константи сили, з репрезентативними значеннями для dsDNA, є:

Розтяжка:$\kappa_{st} = \kappa_{st-entropic} + \kappa_{st-enthalpic}$

$\kappa_{st-entropic} \approx 3k_BT/ \ell_p L_c$

Вигин:$\kappa_b$

$\kappa_b \approx 205 \text{ pN nm}^2$

Скручування:$\kappa_{tw}$

$\kappa_{tw} \approx (86 \text{ nm})k_BT = 353 \text{ pN nm}^2$

Напишіть

Додатковим спотворенням тонких стрижнів є writhe, що відноситься до зв'язаного скручування і намотування, і є важливим фактором супернамотування ДНК. Скручування стрижня може викликати в площині петлі стрижня, наприклад, як зустрічається при спробі намотати садовий шланг. Число Writhe W стрижня відноситься до кількості повних петель, зроблених стрижнем. Writhe може бути позитивним або негативним в залежності від того, чи стрижень перетинає над собою справа наліво або зліва направо. Число скручування T - це число Ω = 2π обертань стрижня, а також може бути позитивним або негативним.

Зв'язкове число L = T+W зберігається в В-формі ДНК, так що скручування може бути перетворено в writhe і навпаки. Оскільки ДНК в клітині природно негативно перекручується в нуклеосомах, топоізомерази використовуються для зміни числа зв'язування шляхом розриву та реформування хребта фосфодіефіру після розслаблення скручування. Негативно перекручена ДНК може бути перетворена в кругову ДНК шляхом локального пузиріння (розмотування в окремі нитки).

_____________________________________

1. Боал Д.Х., Механіка клітини, 2-е изд. (Кембриджський університетський прес, Кембридж, Великобританія, 2012).