9.3: Полімерна еластичність та поведінка сили та розтягування

Ентропна весна

Для подовження полімеру потрібні роботи. Розраховано оборотну роботу по розширенню макромолекули від різниці вільної енергії ланцюга, що утримується між початковим і кінцевим станом. Це природно пов'язано з вільною енергією системи як функція полімерної наскрізної відстані:

\[w_{stretch} = F(r) - F(r_0) = - \int_{r_0}^{r} \vec{f_{rev}} \cdot d \vec{r} \nonumber\]

Для ідеальної ланцюга вільна енергія залежить тільки від ентропії ланцюга:\(F = -TS\). Існує менше конфігураційних станів, доступних для ланцюга, коли ви розтягуєте до більшого розширення. Кількість конфігураційних станів, доступних системі, можна отримати шляхом обчислення конформаційної функції розділення,\(Q_{conf}\). Для розтягування в одновимірному вимірі вільна енергія Гельмгольца - це:

\[\begin{array} {rcl} {dF} & = & {-pdV - SdT + f\cdot dx} \\ {} & = & {-k_B T \ln Q_{conf}} \\ {S_{conf}} & = & {k_B \ln Q_{conf}} \end{array}\nonumber\]

\[f = - \left (\dfrac{\partial F}{\partial x} \right )_{V, T, N} = -k_B T \dfrac{\partial \ln Q_{conf}}{\partial x} = -T \dfrac{\partial S_{conf}}{\partial x} \label{eq9.3.1}\]

Коли ви збільшуєте наскрізну відстань, кількість конфігураційних станів, доступних системі, зменшується. Це вимагає все більш високої сили, оскільки розширення наближається до довжини контуру. Зверніть увагу, що для розтягування ланцюга при більш високій температурі потрібно більше зусилля.

Оскільки це вільно з'єднаний ланцюг, і всі мікростани мають однакову енергію, ми можемо прирівняти конформаційну функцію поділу ланцюга при певному\(x\) розширенні до щільності ймовірності для наскрізних відстаней цього ланцюга

\[Q_{conf} \to P_{fjc} (r)\nonumber\]

Хоча ми тримаємо кінці ланцюга на нерухомому і розтягуємо з кінцями, стриманими уздовж одного напрямку (\(x\)), функція розподілу ймовірностей приймає тривимірну форму, щоб правильно враховувати всі конфігурації ланцюга:\(P_{conf} (r) = P_0 e^{-\beta^2 r^2}\) з\(\beta^2 = 3k_B T/2n \ell^2\) і\(P_0 = \beta^3/\pi^{3/2}\) є постійною. Тоді

\[\ln P_{conf} (r) = -\beta^2 r^2 + \ln P_0 \nonumber\]

Зусилля, необхідне для подовження ланцюга, можна розрахувати з екв. (\(\ref{eq9.3.1}\)) після заміни\(r^2 = x^2 + y^2 + z^2\), що дає

\[f = -2\beta^2 k_B Tx = -\kappa_{st} x\nonumber\]

Отже, ми маємо лінійну залежність між силою та зміщенням, яка є класичною пружиною закону Гука з постійною силою,\(\kappa_{st}\) заданою

\[\kappa_{st} = \dfrac{3k_B T}{n\ell^2} = \dfrac{3k_B T}{\langle r^2 \rangle_0} \nonumber\]

Тут\(\langle r^2 \rangle_0\) мається на увазі середнє квадратне відстань від кінця до кінця для FJC за відсутності будь-яких прикладених зусиль. Пам'ятайте:\(\langle r^2 \rangle_0 = n \ell^2 = \ell L_C\). У разі, якщо вся відновлює сила відбувається за рахунок ентропії, то ми називаємо це ентропною пружиною\(\kappa_{ES}\).

\[\kappa_{ES} = \dfrac{T}{2} \left (\dfrac{\partial^2 S}{\partial x^2} \right )_{N, V, T}\nonumber\]

Це працює для невеликих сил, при цьому сила оборотна. Зверніть увагу, що\(\kappa_{ES}\) підвищується з температурою — як слід очікувати для ентропних відновлювальних сил.

Приклад: Розтягування ДНК ¹

При малій силі:

dsDNA\(\to \kappa_{st} = 5\ pN/nm\)

SSDNA\(\to \kappa_{st} = 160\ pN/nm \to \text{more entropy/more force}\)

При більш високому розширенні ви асимптотично наближаєтеся до довжини контуру.

Сила/розширення випадкового полімеру ходьби

Виведемо поведінку розширення сили для випадкового полімеру ходьби в одному вимірі. Відстань від кінця до кінця є\(r\), довжина сегмента є\(r\), а загальна кількість сегментів -\(n\).

Для будь-якого даного кількість конфігурацій\(r\), доступних полімеру, становить:

\[\Omega = \dfrac{n!}{n_+ ! n_- !}\nonumber\]

Це випливає з визнання того, що розширення випадкового ланцюга ходьби в одному вимірі пов'язане з різницею між кількістю сегментів, які крокують у позитивному напрямку\(n_+\), і тими, що крокують у негативному напрямку\(n_-\). Загальна кількість ступенів дорівнює\(n = n_+ + n_-\). Крім того, наскрізна відстань може бути виражена як

\[r = (n_+ - n_-) \ell = (2n_+ - n) \ell = (n - 2n_-) \ell \label{eq9.3.2}\]

\[n_{\pm} = \dfrac{1}{2} \left (n \pm \dfrac{r}{\ell} \right ) \ \ \ \ \ \ \dfrac{\partial n_{\pm}}{\partial r} = \pm \dfrac{1}{2\ell}\nonumber\]

Потім ми можемо обчислити вільну енергію випадкового ланцюга ходьби, яка виникає в результаті ентропії ланцюга, тобто виродження конфігураційних станів при будь-якому розширенні. Це виглядає як ентропія розрахунку змішування:

\[\begin{array} {rcl} {F} & = & {-k_B T \ln \Omega} \\ {} & = & {-k_B T (n \ln n - n_+ \ln n_+ - n_- \ln n_-)} \\ {} & = & {nk_B T (\phi_+ \ln \phi_+ + \phi_- \ln \phi_-)} \end{array} \nonumber\]

\[\phi_{\pm} = \dfrac{n_{\pm}}{n} = \dfrac{1}{2} (1 \pm x)\nonumber\]

Тут дробове наскрізне подовження ланцюга дорівнює

\[x = \dfrac{r}{L_C}\]

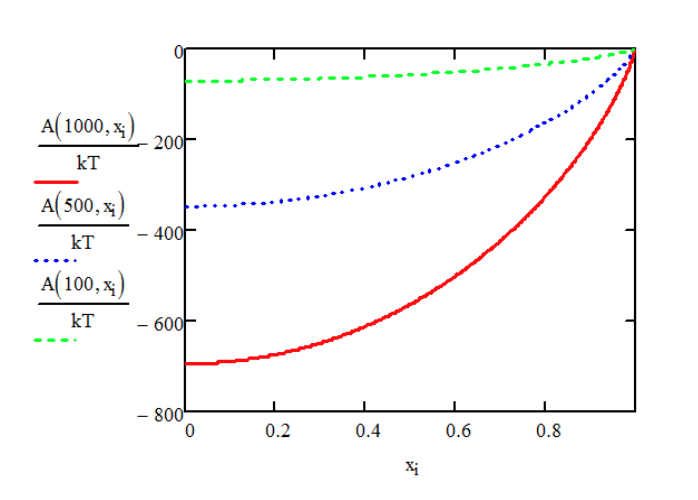
Далі ми можемо обчислити силу, необхідну для розширення полімеру в залежності від\(r\):

\[f = -\dfrac{\partial F}{\partial r} \to \dfrac{\partial F}{\partial \phi_{\pm}} \dfrac{\partial \phi_{\pm}}{\partial r} \ \ \ \ \ \ \dfrac{\partial \phi_{\pm}}{\partial r} = \pm \dfrac{1}{2L_C} \nonumber\]

Використання eq. (\(\ref{eq9.3.2}\))

\[\begin{array} {rcl} {f} & = & {-nk_B T (\ln \phi_+ - \ln \phi_-) \left (\dfrac{1}{2L_C} \right )} \\ {} & = & {-\dfrac{nk_B T}{2L_C} \ln \left (\dfrac{1 + x}{1 - x} \right )} \\ {} & = & {-\dfrac{k_B T}{\ell} \dfrac{1}{2} \ln \left (\dfrac{1 + x}{1 - x} \right )} \end{array}\nonumber\]

\[f = -\dfrac{k_B T}{\ell} \text{tanh}^{-1} (x) \label{eq9.3.4}\]

де\(I\) використовуються відносини:\(\ln \left (\dfrac{1 + x}{1 - x} \right ) = 2 \text{tanh}^{-1} (x)\). Зверніть увагу, тут сили масштабуються в одиницях\(k_B T/\ell\). Для\(x \ll 1\) малих сил\(\text{tanh}^{-1} (x) \approx x\) і ур. (\(\ref{eq9.3.4}\)) дає\(f \approx \dfrac{k_B T}{\ell L_C} r\). Це дає поведінку закону Гука з константою ентропної сили, очікуваної для 1D ланцюга. Для 3D-ланцюга ми очікуємо:\(f \approx \dfrac{3k_B T}{\ell L_C} r\). Пружинна постійна шкала з розмірністю.

Взаємозв'язок між положенням, силою та функцією розділення

Тепер давайте зробимо це трохи уважніше. З класичної статистичної механіки функція розділення

\[Q = \int \int dr^{3N} dp^{3N} \exp (-H/k_B T)\nonumber\]

Де\(H\) знаходиться гамільтоніан для системи. Середнє значення положення частинки, описаної гамільтоном, становить

\[\langle x \rangle = \dfrac{1}{Q} \int \int dr^3 dp^3 x \exp (-H/k_B T)\nonumber\]

Якщо гамільтоніан приймає форму

\[H = -f \cdot x \nonumber\]

Тоді

\[\langle x \rangle = \dfrac{k_B T}{Q} \left (\dfrac{\partial Q}{\partial f} \right )_{V, T, N} = k_B T \left (\dfrac{\partial \ln Q}{\partial f} \right )_{V, T, N} \nonumber\]

Це описує середнє подовження ланцюга, якщо сила прикладена до кінців.

Поведінка сили та розширення для вільно з'єднаного ланцюга

Використання виразів вище і\(Q = q^N\)

\[q_{conf} = \int \int dr^3 dp^3 e^{-U/kT} e^{\vec{f} \cdot \vec{r}/k_B T} \ \ \ \ \ \ \ \langle r \rangle = Nk_B T \left (\dfrac{\partial \ln q_{conf}}{\partial f} \right )_{U, r, n}\nonumber\]

Тут ми також вставили загальний гамільтоніан, який враховує потенціал внутрішньої ланцюгової взаємодії та силу, що знаходиться на ланцюзі:\(H = U - \vec{f} \cdot \vec{r}\). Для\(N\) вільно з'єднаних ланцюгів з n відрізками ми встановлюємо\(U \to 0\), і орієнтуємося на силу, що чиниться на кожен відрізок ланцюга.

\[\vec{f} \cdot \vec{r} = \sum_{i = 1}^{n} \vec{f} \cdot \vec{\ell_i} = f \ell \sum_{i = 1}^{n} \cos \theta_i\nonumber\]

Розглядаючи сегменти як незалежні та інтегруються над усіма\(\theta\), ми виявляємо, що

\[q_{conf} (f) = \dfrac{2\pi \text{sinh} \varphi}{\varphi} \nonumber\]

\[\langle r \rangle = n \ell \left [\text{coth} \varphi - \dfrac{1}{\varphi} \right ] \]

де параметр безодиничної сили

\[\varphi = \dfrac{f \ell}{k_B T}\]

Як і раніше, величина сили виражається щодо\(k_B T/\ell\). Зверніть увагу, що цей розрахунок призначений для середнього розширення, яке виникає в результаті фіксованого зусилля. Якщо нам потрібна сила, необхідна для даного середнього розширення, то нам потрібно інвертувати вираз. Зауважте, функціональна форма кривої силового розширення в екв. відрізняється від того, що ми знайшли для 1D випадкової ходьби в еквалайзері. (\(\ref{eq9.3.4}\)). Ми не очікуємо однакової форми для цих проблем, оскільки наш приклад випадкової ходьби був на квадратній решітці, а FJC поширюється радіально у всіх напрямках.

деривація

Для однієї полімерної ланцюга:

\[\begin{array} {rcl} {q} & = & {\int \int dr^3 dp^3 e^{U/k_B T} e^{-f \cdot r/k_B T}} \\ {P(r)} & = & {\dfrac{1}{q} e^{-U/k_B T} e^{f \cdot r/k_B T}} \\ {\langle r \rangle} & = & {\dfrac{k_B T}{q} \left (\dfrac{\partial \ln q}{\partial f} \right )_u} \end{array}\nonumber\]

У випадку з Вільно з'єднаним ланцюгом, набір\(U \to 0\).

\[\vec{f} \cdot \vec{r} = \vec{f} \cdot \sum_{i =1}^{n} \vec{\ell_i} = f \ell \sum_{i = 1}^{n} \cos \theta_i \nonumber\]

Розмежовані сегменти:

\[\begin{array} {rcl} {q} & \approx & {\int dr^3 \exp \left (\sum_i \dfrac{f \ell}{k_B T} \cos \theta_i \right )} \\ {} & = & {(\int_{0}^{2\pi} \int_{0}^{\pi} \exp [\varphi \cos \theta] \sin \theta d \theta d \phi)^n} \\ {} & = & {\left (\dfrac{2\pi \text{sinh} (\varphi)}{\varphi} \right )^n} \\ {\langle r \rangle} & = & {k_B T \dfrac{\partial}{\partial f} \ln q} \\ {} & = & {nk_B T \dfrac{\partial}{\partial f} \left [\ln \left \{\dfrac{2\pi \text{sinh} (\varphi)}{\varphi} \right \} \right ] \ \ \ \ \ \ \text{coth} (x) = \dfrac{e^x + e^{-x}}{e^x - e^{-x}}} \\ {\langle r \rangle} & = & {n \ell [\text{coth} (\varphi) - \varphi^{-1}]} \\ {\text{or } \langle x \rangle = \text{coth} (\varphi) - \varphi^{-1}} & \ & {\text{ The average fractional extension: } \langle x \rangle = \langle r \rangle / L_C} \end{array} \nonumber\]

Тепер давайте розглянемо поведінку виразу for\(\langle x \rangle\) — також відомого як функція Ланжевена.

\[\langle r \rangle = n \ell [\text{coth} (\varphi) - \varphi^{-1}]\]

Дивлячись на ліміти:

• Слабка сила\((\varphi \ll 1): f \ll k_B T/\ell\)
  Вставка і усічення розширення:\(\text{coth} \varphi = \dfrac{1}{\varphi} + \dfrac{1}{3} \varphi - \dfrac{1}{45} \varphi^3 + \dfrac{2}{945} \varphi^5 + \cdots\), отримуємо
  \[\begin{array} {rcl} {\langle x \rangle} & = & {\dfrac{\langle r \rangle}{L_C} \approx \dfrac{1}{3} \varphi} \\ {\langle r \rangle} & \approx & {\dfrac{1}{3} \dfrac{n \ell^2}{k_B T} f} \\ {\text{or } \ \ \ f} & = & {\dfrac{3k_B T}{n \ell^2} \langle r \rangle = \kappa_{ES} \langle r \rangle} \end{array} \nonumber\]
  Зверніть увагу, що ця межа має очікувану лінійну залежність між силою і зміщенням, яка регулюється ентропною постійною пружини.
• Сильна сила (\(\varphi \gg 1\)). \(f \gg k_B T / \ell\)Взявши ліміт\(\text{coth} (x) \to 1\).
  \[\langle r \rangle \simeq n \ell \left [1 - \dfrac{1}{\varphi} \right ] \longleftarrow \lim_{f \to \infty} = \lim_{\alpha \to \infty} = L_C \text{ Contour length} \nonumber\]
  \[\text{Or } f = \dfrac{k_B T}{\ell} \dfrac{1}{1 - \langle x \rangle} \text{ where } \langle x \rangle = \dfrac{\langle r \rangle}{L_C} \nonumber\]
  Для сильної межі сили поведінка розширення сили масштабується як,\(x \sim 1 - f^{-1}\).

Отже, яка робота потрібна для подовження ланцюга?

При малих силах ми можемо інтегруватися над лінійною поведінкою силового розширення. За цих умов, щоб поширитися від\(r\) до\(r+\Delta r\), ми маємо

\[w_{rev} = \int_0^{\Delta r} \kappa_{ES} r dr = \dfrac{3k_B T}{2n \ell^2} \Delta r^2\nonumber\]

Сила/розширення черв'ячного ланцюга

Для черв'ячної моделі ланцюга ми виявили, що дисперсія на відстані від кінця до кінця була

\[\langle r^2 \rangle = 2 \ell_p L_C - 2 \ell_p^2 (1 - e^{-L_C/\ell_p}) \label{eq9.3.8}\]

де\(L_C\) довжина контуру, а довжина наполегливості була пов'язана з постійною силою згинання як\(\ell_p = \dfrac{\kappa_b}{k_B T}\). Обмежуюча поведінка для ур. (\(\ref{eq9.3.8}\)) це:

\[\begin{array} {lclcrclcl} {\text{rigid:}} & \ \ & {\ell_p \gg L_C} & \ \ & {\langle r^2 \rangle} & \propto & {L_C^2} & \ \ & {} \\ {\text{flexible:}} & \ \ & {\ell_p \ll L_C} & \ \ & {\langle r^2 \rangle} & \sim & {2L_C \ell_p} & \ \ & {\therefore \text{for WLC}} \\ {} & \ \ & {} & \ \ & {} & = & {n_e \ell_e^2} & \ \ & {(2 \ell_p = \ell_e)} \end{array} \nonumber\]

Слідуючи подібному підходу до FJC вище, неможливо знайти точне рішення для поведінки силового розширення WLC, але можна показати поведінку розширення сили в жорстких і гнучких межах.

Установка\(2\ell_p = \ell_e\)\(\varphi = f\ell_e /k_B T\), і використання дробового розширення\(\langle x \rangle = \dfrac{\langle r \rangle}{L_C}\):

1. Слабка сила (\(\varphi \ll 1\)) Очікувана поведінка закону Гука
   \[f \ell_e \ll k_B T \ \ \ \ \ \ \ \ \ \ f = \dfrac{3k_B T}{\ell_e L_C} \longrightarrow \dfrac{f \ell_e}{k_B T} = 3\langle x \rangle \nonumber\]
   Для слабкої межі сили поведінка розширення сили масштабується як,\(x \sim f\).
2. Сильна сила (\(\varphi \gg 1\))
   \[f \ell_e \gg k_B T \ \ \ \ \ \ \ \ \langle r \rangle = L_C \left (1 - \dfrac{1}{2\sqrt{\varphi}} \right ) \longrightarrow \dfrac{f \ell_e}{k_B T} = \dfrac{1}{4(1 - \langle x \rangle)^2} \nonumber\]
   Для сильної межі сили поведінка розширення сили масштабується як,\(x \sim 1 - f^{-1/2}\).

Приблизний вираз для комбінованого результату (від Bustamante):

\[\dfrac{f\ell_p}{kT} = \dfrac{1}{4(1 - \langle x \rangle)^2} - \dfrac{1}{4} + \langle x \rangle\]

_____________________________

1. А. М. ван Ойєн і Дж. Лопаро, одномолекулярні дослідження реплісоми, Анну. Преподобний Біофіс. 39, 429—448 (2010).