7.2: Тести значущості для нормальних розподілів
- Page ID
- 17834
Звичайний розподіл - це найпоширеніший розподіл даних, які ми збираємо. Оскільки площа між будь-якими двома межами нормальної кривої розподілу чітко визначена, легко побудувати та оцінити тести на значущість.
Властивості звичайного розподілу можна переглянути у главах 5 та 6.
Порівняння\(\overline{X}\) з\(\mu\)
Одним із способів перевірки нового аналітичного методу є аналіз зразка, який містить відому кількість аналіту\(\mu\). Щоб судити про точність методу, ми аналізуємо кілька частин зразка, визначаємо середню кількість аналіту у зразку та використовуємо тест на значущість\(\overline{X}\) для порівняння\(\mu\).\(\overline{X}\) Нульова гіпотеза полягає в тому, що різниця між\(\overline{X}\) і\(\mu\) пояснюється невизначеними помилками, які впливають на наше визначення\(\overline{X}\). Альтернативна гіпотеза полягає в тому, що різниця між\(\overline{X}\) і\(\mu\) занадто велика, щоб пояснюватися невизначеною помилкою.
\[H_0 \text{: } \overline{X} = \mu \nonumber\]
\[H_A \text{: } \overline{X} \neq \mu \nonumber\]
Тестова статистика - t exp, яку ми підставляємо в довірчий інтервал для\(\mu\)
\[\mu = \overline{X} \pm \frac {t_\text{exp} s} {\sqrt{n}} \nonumber\]
Перестановка цього рівняння і рішення для\(t_\text{exp}\)
\[t_\text{exp} = \frac {|\mu - \overline{X}| \sqrt{n}} {s} \nonumber\]
дає значення,\(t_\text{exp}\) коли\(\mu\) знаходиться на правому краю або на лівому краї довірчого інтервалу зразка (рис.\(\PageIndex{1a}\)).
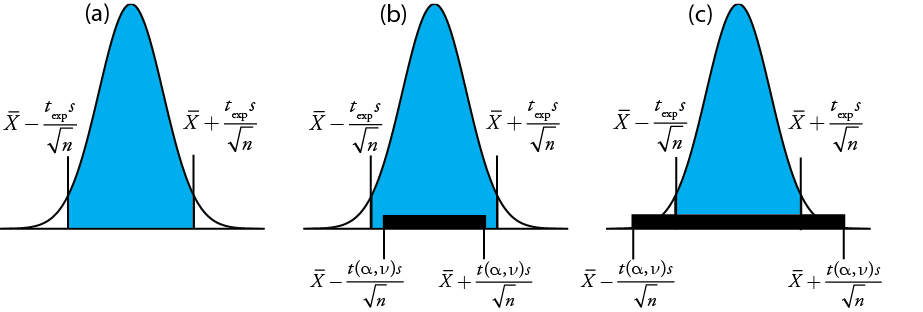
Щоб визначити, чи слід зберігати або відхиляти нульову гіпотезу, ми порівняємо значення t exp з критичним значенням\(t(\alpha, \nu)\), де\(\alpha\) рівень довіри та\(\nu\) ступені свободи для вибірки. Критичне значення\(t(\alpha, \nu)\) визначає найбільший довірчий інтервал, пояснений невизначеною помилкою. Якщо\(t_\text{exp} > t(\alpha, \nu)\), то довірчий інтервал нашої вибірки більше, ніж той, що пояснюється невизначеними помилками (рис.\(\PageIndex{1}\) b). У цьому випадку ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу. Якщо\(t_\text{exp} \leq t(\alpha, \nu)\), то довірчий інтервал нашої вибірки менше, ніж пояснюється невизначеною помилкою, і ми зберігаємо нульову гіпотезу (рис.\(\PageIndex{1}\) С). Приклад\(\PageIndex{1}\) дає типове застосування цього тесту значущості, який відомий як t -тест\(\overline{X}\) to\(\mu\). Ви знайдете значення для\(t(\alpha, \nu)\) в Додатку 2.
Перш ніж визначити кількість Na 2 CO 3 в зразку, ви вирішили перевірити свою процедуру, проаналізувавши стандартний зразок, який становить 98,76% w/w Na 2 CO 3. П'ять реплікацій визначення% w/w Na 2 CO 3 в стандарті дають наступні результати
\(98.71 \% \quad 98.59 \% \quad 98.62 \% \quad 98.44 \% \quad 98.58 \%\)
Використовуючи\(\alpha = 0.05\), чи є якісь докази того, що аналіз дає неточні результати?
Рішення
Середнє і стандартне відхилення для п'яти випробувань
\[\overline{X} = 98.59 \quad \quad \quad s = 0.0973 \nonumber\]
Оскільки немає підстав вважати, що результати для стандарту повинні бути більшими або меншими\(\mu\), ніж, доречний двохвіст t -тест. Нульова гіпотеза та альтернативна гіпотеза
\[H_0 \text{: } \overline{X} = \mu \quad \quad \quad H_\text{A} \text{: } \overline{X} \neq \mu \nonumber\]
Статистика тесту, t exp, становить
\[t_\text{exp} = \frac {|\mu - \overline{X}|\sqrt{n}} {2} = \frac {|98.76 - 98.59| \sqrt{5}} {0.0973} = 3.91 \nonumber\]
Критичне значення для t (0,05, 4) з додатка 2 - 2,78. Оскільки t exp більше t (0,05, 4), відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу. На рівні довіри 95% різниця між\(\overline{X}\) і\(\mu\) є занадто великою, щоб пояснюватися невизначені джерела помилки, що говорить про наявність визначеного джерела помилки, що впливає на аналіз.
Є ще один спосіб інтерпретації результату цього t -тесту. Знаючи, що t exp дорівнює 3,91 і що існує 4 ступені свободи, ми використовуємо Додаток 2 для оцінки значення,\(\alpha\) що відповідає t (\(\alpha\), 4) з 3.91. З додатка 2, т (0,02, 4) дорівнює 3,75, а т (0,01, 4) дорівнює 4,60. Хоча ми можемо відхилити нульову гіпотезу на рівні довіри 98%, ми не можемо відхилити її на рівні довіри 99%. Для обговорення переваг цього підходу див. Дж. С. Стерн і Г.Д. Сміт «Просіювання доказів - що не так з тестами значущості?» БМЖ 2001, 322, 226—231.
Раніше ми говорили про те, що ми повинні проявляти обережність, інтерпретуючи результат статистичного аналізу. Ми будемо продовжувати повертатися до цього моменту, оскільки це важливий. Визначивши, що результат неточний, як ми це робили в прикладі\(\PageIndex{1}\), наступним кроком є виявлення і виправлення помилки. Однак перш ніж витрачати час і гроші на це, ми спочатку повинні критично вивчити наші дані. Наприклад, чим менше значення s, тим більше значення t exp. Якщо стандартне відхилення для нашого аналізу нереально мало, то ймовірність помилки 2 типу зростає. Включення декількох додаткових повторюваних аналізів стандарту та переоцінка t -тесту може посилити наші докази щодо визначеної помилки, або це може показати нам, що немає доказів для визначеної помилки.
Порівняння\(s^2\) з\(\sigma^2\)
Якщо ми регулярно аналізуємо певну вибірку, ми можемо встановити очікувану дисперсію для аналізу.\(\sigma^2\) Це часто трапляється, наприклад, у клінічній лабораторії, яка щодня аналізує сотні зразків крові. Кілька повторюваних аналізів одного зразка дають дисперсію зразка, s 2, значення якої може або не може суттєво відрізнятися від\(\sigma^2\).
Ми можемо використовувати F -тест, щоб оцінити, чи є різниця між s 2 і\(\sigma^2\) є значною. Нульова гіпотеза є\(H_0 \text{: } s^2 = \sigma^2\) і альтернативна гіпотеза є\(H_\text{A} \text{: } s^2 \neq \sigma^2\). Тестова статистика для оцінки нульової гіпотези - F exp, яка дається як або
\[F_\text{exp} = \frac {s^2} {\sigma^2} \text{ if } s^2 > \sigma^2 \text{ or } F_\text{exp} = \frac {\sigma^2} {s^2} \text{ if } \sigma^2 > s^2 \nonumber\]
в залежності від того, чи є s 2 більше або менше, ніж\(\sigma^2\). Цей спосіб визначення F exp гарантує, що його значення завжди більше або дорівнює одиниці.
Якщо нульова гіпотеза вірна, то F exp повинна дорівнювати одиниці; однак через невизначені помилки F exp, як правило, більше одиниці. Критичне значення є найбільшим значенням F exp\(F(\alpha, \nu_\text{num}, \nu_\text{den})\), яке ми можемо віднести до невизначеної помилки\(\alpha\), враховуючи заданий рівень значущості, і ступені свободи для дисперсії в чисельнику\(\nu_\text{num}\), і дисперсія в знаменнику,\(\nu_\text{den}\). Ступінь свободи для s 2 дорівнює n — 1, де n - кількість реплікацій, що використовуються для визначення дисперсії вибірки, а ступінь свободи для\(\sigma^2\) визначається як нескінченність,\(\infty\). Критичні значення F для\(\alpha = 0.05\) перераховані в Додатку 3 як для однохвостих, так і для двохвостих F -тестів.
Процес виробника для аналізу таблеток аспірину має відому дисперсію 25. Зразок з 10 таблеток аспірину відбирається і аналізується на кількість аспірину, даючи наступні результати в мг аспірину/таблетці.
\(254 \quad 249 \quad 252 \quad 252 \quad 249 \quad 249 \quad 250 \quad 247 \quad 251 \quad 252\)
Визначте, чи є докази значної різниці між дисперсією вибірки та очікуваною дисперсією при\(\alpha = 0.05\).
Рішення
Дисперсія для проби 10 таблеток становить 4,3. Нульова гіпотеза та альтернативні гіпотези
\[H_0 \text{: } s^2 = \sigma^2 \quad \quad \quad H_\text{A} \text{: } s^2 \neq \sigma^2 \nonumber\]
і значення для F exp дорівнює
\[F_\text{exp} = \frac {\sigma^2} {s^2} = \frac {25} {4.3} = 5.8 \nonumber\]
Критичне значення для F (0,05,\(\infty\), 9) з додатка 3 - 3,333. Оскільки F exp більше F (0,05,, 9)\(\infty\), ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу про те, що існує значна різниця між дисперсією вибірки та очікуваною дисперсією. Одним з пояснень різниці може бути те, що таблетки аспірину не були обрані випадковим чином.
Порівняння відхилень для двох зразків
Ми можемо розширити F -тест, щоб порівняти дисперсії для двох зразків, A і B, переписавши наше рівняння для F exp як
\[F_\text{exp} = \frac {s_A^2} {s_B^2} \nonumber\]
визначення A і B таким чином, щоб значення F exp було більше або дорівнювало 1.
У таблиці нижче наведені результати двох експериментів з визначення маси циркулюючої американської пенні. Визначте, чи є різниця в дисперсіях цих аналізів на\(\alpha = 0.05\).
| Перший експеримент | Другий експеримент | ||
|---|---|---|---|
| Пенні | Маса (г) | Пенні | Маса (г) |
| 1 | 3.080 | 1 | 3.052 |
| 2 | 3.094 | 2 | 3.141 |
| 3 | 3.107 | 3 | 3.083 |
| 4 | 3.056 | 4 | 3.083 |
| 5 | 3.112 | 5 | 3.048 |
| 6 | 3.174 | ||
| 7 | 3.198 | ||
Рішення
Стандартні відхилення для двох експериментів складають 0,051 для першого експерименту (А) і 0,037 для другого експерименту (B). Нульова та альтернативна гіпотези
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_\text{A} \text{: } s_A^2 \neq s_B^2 \nonumber\]
і значення F exp дорівнює
\[F_\text{exp} = \frac {s_A^2} {s_B^2} = \frac {(0.051)^2} {(0.037)^2} = \frac {0.00260} {0.00137} = 1.90 \nonumber\]
З Додатка 3 критичне значення для F (0,05, 6, 4) дорівнює 9.197. Оскільки F exp < F (0,05, 6, 4), ми зберігаємо нульову гіпотезу. Немає жодних доказів,\(\alpha = 0.05\) щоб припустити, що різниця в дисперсіях є значною.
Порівняння засобів для двох зразків
На результат аналізу впливають три фактори: метод, вибірка та аналітик. Ми можемо вивчити вплив цих факторів, проводячи експерименти, в яких ми змінюємо один фактор, утримуючи постійними інші фактори. Наприклад, для порівняння двох аналітичних методів ми можемо мати одного і того ж аналітика застосувати кожен метод до одного і того ж зразка, а потім вивчити отримані кошти. Подібним чином ми можемо розробляти експерименти для порівняння двох аналітиків або порівняння двох зразків.
Перш ніж розглядати тести на значущість для порівняння засобів двох вибірок, нам потрібно зрозуміти різницю між непарними даними і парними даними. Це критична відмінність, і важливо навчитися розрізняти ці два типи даних. Ось два простих приклади, які підкреслюють різницю між непарними даними та парними даними. У кожному прикладі мета полягає в тому, щоб порівняти два залишки, зважуючи копійки.
- Приклад 1: Ми збираємо 10 копійок і зважуємо кожну копійку на кожному балансі. Це приклад парних даних, оскільки ми використовуємо ті ж 10 копійок для оцінки кожного балансу.
- Приклад 2: Ми збираємо 10 копійок і ділимо їх на дві групи по п'ять копійок кожна. Зважуємо копійки в першій групі на одному балансі і зважуємо другу групу копійок на іншому балансі. Зверніть увагу, що жодна копійка не зважується на обох залишках. Це приклад непарних даних, оскільки ми оцінюємо кожен баланс, використовуючи різну вибірку копійок.
В обох прикладах вибірки 10 копійок були взяті з однієї і тієї ж популяції; різниця полягає в тому, як ми відбирали цю популяцію. Ми дізнаємося, чому ця відмінність важлива, коли ми переглядаємо тест на значущість для парних даних; однак спочатку ми представляємо тест на значущість для непарних даних.
Один простий тест для визначення того, чи є дані парними або непарними, - це подивитися на розмір кожної вибірки. Якщо зразки мають різний розмір, то дані повинні бути непарними. Зворотне не відповідає дійсності. Якщо два зразки однакового розміру, вони можуть бути парними або непарними.
Непарні дані
Розглянемо два аналізи, A і B, із засобами\(\overline{X}_A\) і\(\overline{X}_B\), і стандартні відхилення s A і s B. Довірчі інтервали для\(\mu_A\) і для\(\mu_B\) є
\[\mu_A = \overline{X}_A \pm \frac {t s_A} {\sqrt{n_A}} \nonumber\]
\[\mu_B = \overline{X}_B \pm \frac {t s_B} {\sqrt{n_B}} \nonumber\]
де n A і n B - розміри вибірки для A і для B. Наша нульова гіпотеза полягає в тому\(H_0 \text{: } \mu_A = \mu_B\), що будь-яка різниця між\(\mu_A\) і\(\mu_B\) є результатом невизначеної помилки, які впливають на аналіз. Альтернативна гіпотеза полягає в тому\(H_A \text{: } \mu_A \neq \mu_B\), що різниця між\(\mu_A\) і\(\mu_B\) занадто велика, щоб пояснюватися невизначеною помилкою.
Щоб вивести рівняння для t exp, ми вважаємо, що\(\mu_A\) дорівнює\(\mu_B\), і об'єднаємо рівняння для двох довірчих інтервалів
\[\overline{X}_A \pm \frac {t_\text{exp} s_A} {\sqrt{n_A}} = \overline{X}_B \pm \frac {t_\text{exp} s_B} {\sqrt{n_B}} \nonumber\]
Розв'язування\(|\overline{X}_A - \overline{X}_B|\) та використання поширення невизначеності, дає
\[|\overline{X}_A - \overline{X}_B| = t_\text{exp} \times \sqrt{\frac {s_A^2} {n_A} + \frac {s_B^2} {n_B}} \nonumber\]
Нарешті, вирішуємо для t exp
\[t_\text{exp} = \frac {|\overline{X}_A - \overline{X}_B|} {\sqrt{\frac {s_A^2} {n_A} + \frac {s_B^2} {n_B}}} \nonumber\]
і порівняти його з критичним значенням\(t(\alpha, \nu)\), де\(\alpha\) ймовірність помилки типу 1, а\(\nu\) це ступені свободи.
Поки що наша розробка цього t -тесту схожа на те, що\(\overline{X}\) для порівняння з\(\mu\), і все ж ми не маємо достатньої інформації для оцінки t -тесту. Бачите проблему? З двома незалежними наборами даних незрозуміло, скільки ступенів свободи ми маємо.
Припустимо, що\(s_A^2\)\(s_B^2\) розбіжності і дають оцінки однакові\(\sigma^2\). У цьому випадку ми можемо замінити\(s_A^2\) і\(s_B^2\) з об'єднаною дисперсією\(s_\text{pool}^2\), що є кращою оцінкою для дисперсії. Таким чином, наше рівняння для\(t_\text{exp}\) стає
\[t_\text{exp} = \frac {|\overline{X}_A - \overline{X}_B|} {s_\text{pool} \times \sqrt{\frac {1} {n_A} + \frac {1} {n_B}}} = \frac {|\overline{X}_A - \overline{X}_B|} {s_\text{pool}} \times \sqrt{\frac {n_A n_B} {n_A + n_B}} \nonumber\]
де s басейн, об'єднане стандартне відхилення,
\[s_\text{pool} = \sqrt{\frac {(n_A - 1) s_A^2 + (n_B - 1)s_B^2} {n_A + n_B - 2}} \nonumber\]
Знаменник цього рівняння показує нам, що ступені свободи для об'єднаного стандартного відхилення є\(n_A + n_B - 2\), яке також є ступенями свободи для t -тесту. Зверніть увагу, що ми втрачаємо два ступені свободи, тому що розрахунки для\(s_A^2\) і\(s_B^2\) вимагають попереднього розрахунку\(\overline{X}_A\) amd\(\overline{X}_B\).
Отже, як ви визначаєте, якщо це нормально, щоб об'єднати дисперсії? Використовуйте F-тест.
Якщо\(s_A^2\) і значно\(s_B^2\) відрізняються, то обчислюємо t exp, використовуючи наступне рівняння. У цьому випадку ми знаходимо ступені свободи, використовуючи наступне нав'язуюче рівняння.
\[\nu = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {\left( \frac {s_A^2} {n_A} \right)^2} {n_A + 1} + \frac {\left( \frac {s_B^2} {n_B} \right)^2} {n_B + 1}} - 2 \nonumber\]
Оскільки ступені свободи повинні бути цілим числом, ми округляємо до найближчого цілого числа значення\(\nu\) отриманого з цього рівняння.
Рівняння вище для ступенів свободи взято з Міллера, J.C.; Міллер, J.N. статистика аналітичної хімії, 2-е видання, Елліс-Хорвард: Чичестер, Великобританія, 1988. У 6-му виданні автори відзначають, що запропоновано кілька різних рівнянь для числа ступенів свободи для t, коли s A і s B відрізняються, відображаючи той факт, що визначення ступенів свободи і наближення. Альтернативним рівнянням, яке використовується статистичними програмними пакетами, такими як R, Minitab, Excel, є
\[\nu = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {\left( \frac {s_A^2} {n_A} \right)^2} {n_A - 1} + \frac {\left( \frac {s_B^2} {n_B} \right)^2} {n_B - 1}} = \frac {\left( \frac {s_A^2} {n_A} + \frac {s_B^2} {n_B} \right)^2} {\frac {s_A^4} {n_A^2(n_A - 1)} + \frac {s_B^4} {n_B^2(n_B - 1)}} \nonumber\]
Для типових задач в аналітичній хімії обчислені ступені свободи досить нечутливі до вибору рівняння.
Незалежно від того, як ми обчислюємо t exp, ми відкидаємо нульову гіпотезу, якщо t exp більше,\(t(\alpha, \nu)\) і зберігаємо нульову гіпотезу, якщо t exp менше або дорівнює\(t(\alpha, \nu)\).
Приклад\(\PageIndex{3}\) дає результати двох експериментів для визначення маси циркулюючої американської пенні. Визначте, чи є різниця в засобах цих аналізів на\(\alpha = 0.05\).
Рішення
Спочатку ми використовуємо F -тест, щоб визначити, чи можемо ми об'єднати відхилення. Ми завершили цей аналіз на прикладі\(\PageIndex{3}\), не знайшовши доказів істотної різниці, а це означає, що ми можемо об'єднати стандартні відхилення, отримавши
\[s_\text{pool} = \sqrt{\frac {(7 - 1)(0.051)^2 + (5 - 1)(0.037)^2} {7 + 5 - 2}} = 0.0459 \nonumber\]
з 10 ступенями свободи. Для порівняння засобів використовуємо наступну нульову гіпотезу і альтернативні гіпотези:
\[H_0 \text{: } \mu_A = \mu_B \quad \quad \quad H_A \text{: } \mu_A \neq \mu_B \nonumber\]
Оскільки ми використовуємо об'єднане стандартне відхилення, ми обчислюємо t exp як
\[t_\text{exp} = \frac {|3.117 - 3.081|} {0.0459} \times \sqrt{\frac {7 \times 5} {7 + 5}} = 1.34 \nonumber\]
Критичне значення для t (0,05, 10), з додатка 2, дорівнює 2,23. Оскільки t exp менше t (0,05, 10), ми зберігаємо нульову гіпотезу. Бо у\(\alpha = 0.05\) нас немає доказів того, що два набори копійок істотно відрізняються.
Одним із методів визначення %w/w Na 2 CO 3 в кальцинованій соді є використання кислотно-основного титрування. Коли два аналітики аналізують один і той же зразок кальцинованої соди, вони отримують результати, показані тут.
Аналітик А:\(86.82 \% \quad 87.04 \% \quad 86.93 \% \quad 87.01 \% \quad 86.20 \% \quad 87.00 \%\)
Аналітик B:\(81.01 \% \quad 86.15 \% \quad 81.73 \% \quad 83.19 \% \quad 80.27 \% \quad 83.93 \% \quad\)
Визначте, чи значна різниця в середніх значеннях при\(\alpha = 0.05\).
Рішення
Ми починаємо з звітності про середнє і стандартне відхилення для кожного аналітика.
\[\overline{X}_A = 86.83\% \quad \quad s_A = 0.32\% \nonumber\]
\[\overline{X}_B = 82.71\% \quad \quad s_B = 2.16\% \nonumber\]
Щоб визначити, чи можемо ми використовувати об'єднане стандартне відхилення, ми спочатку завершуємо F-тест, використовуючи наступні нульові та альтернативні гіпотези.
\[H_0 \text{: } s_A^2 = s_B^2 \quad \quad \quad H_A \text{: } s_A^2 \neq s_B^2 \nonumber\]
Розрахувавши F exp, отримаємо значення
\[F_\text{exp} = \frac {(2.16)^2} {(0.32)^2} = 45.6 \nonumber\]
Оскільки F exp більше критичного значення 7.15 для F (0,05, 5, 5) з Додатка 3, ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу про те, що існує значна різниця між дисперсіями; таким чином, ми не можемо обчислити об'єднаний стандарт відхилення.
Для порівняння засобів для двох аналітиків ми використовуємо наступні нульові та альтернативні гіпотези.
\[H_0 \text{: } \overline{X}_A = \overline{X}_B \quad \quad \quad H_A \text{: } \overline{X}_A \neq \overline{X}_B \nonumber\]
Оскільки ми не можемо об'єднати стандартні відхилення, ми обчислюємо t exp як
\[t_\text{exp} = \frac {|86.83 - 82.71|} {\sqrt{\frac {(0.32)^2} {6} + \frac {(2.16)^2} {6}}} = 4.62 \nonumber\]
і обчислити ступені свободи як
\[\nu = \frac {\left( \frac {(0.32)^2} {6} + \frac {(2.16)^2} {6} \right)^2} {\frac {\left( \frac {(0.32)^2} {6} \right)^2} {6 + 1} + \frac {\left( \frac {(2.16)^2} {6} \right)^2} {6 + 1}} - 2 = 5.3 \approx 5 \nonumber\]
З Додатка 2 критичне значення для t (0,05, 5) дорівнює 2,57. Оскільки t exp більше, ніж t (0,05, 5), ми відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу про те, що засоби для двох аналітиків значно відрізняються\(\alpha = 0.05\).
Парні дані
Припустимо, ми оцінюємо новий метод контролю концентрації глюкози в крові у пацієнтів. Важливою частиною оцінки нового методу є порівняння його з усталеним методом. Який найкращий спосіб зібрати дані для цього дослідження? Оскільки різниця в рівні глюкози в крові серед пацієнтів велика, ми можемо не виявити невелику, але істотну різницю між методами, якщо ми використовуємо різних пацієнтів для збору даних для кожного методу. Використання парних даних, в яких ми аналізуємо кров кожного пацієнта за допомогою обох методів, запобігає значній дисперсії всередині популяції від негативного впливу на t -тест засобів.
Типові рівні глюкози в крові для більшості людей, які не мають діабету, коливається між 80-120 мг/дл (4.4—6.7 мМ), підвищуючись до 140 мг/дл (7,8 мМ) незабаром після їжі. Більш високі рівні є загальними для осіб, які є попередньо діабетичної або діабетичної.
Коли ми використовуємо парні дані, ми спочатку обчислюємо індивідуальні відмінності, d i, між парними реакціями кожного зразка. Використовуючи ці індивідуальні відмінності, ми потім обчислюємо середню різницю\(\overline{d}\), і стандартне відхилення відмінностей, s d. Нульова гіпотеза полягає в тому\(H_0 \text{: } d = 0\), що немає різниці між двома зразками та альтернативною гіпотезою\(H_A \text{: } d \neq 0\), полягає в тому, що різниця між двома зразками є значною.
Тестова статистика, t exp, походить від довірчого інтервалу навколо\(\overline{d}\)
\[t_\text{exp} = \frac {|\overline{d}| \sqrt{n}} {s_d} \nonumber\]
де n - кількість парних зразків. Як і для інших форм t -тесту, ми порівнюємо t exp до\(t(\alpha, \nu)\), де ступені свободи\(\nu\), є n — 1. Якщо t exp більше\(t(\alpha, \nu)\), то відкидаємо нульову гіпотезу і приймаємо альтернативну гіпотезу. Ми зберігаємо нульову гіпотезу, якщо t exp менше або дорівнює t (a, o). Це відоме як парний t-тест.
Marecek et. al. розробили новий електрохімічний метод швидкого визначення концентрації антибіотика моненсін у чанах бродіння [Marecek, V.; Janchenova, H.; Brezina, M; Betti, M. Чим. Акт 1991, 244, 15—19]. Стандартним методом аналізу є тест на мікробіологічну активність, який є одночасно складним для завершення і трудомістким. Зразки збирали з ферментаційних чанів в різний час під час виробництва і аналізували на концентрацію моненсіна обома методами. Результати, у частках на тисячу (ppt), наведені в наступній таблиці.
| Зразок | Мікробіологічні | електрохімічний |
|---|---|---|
| 1 | 129.5 | 132.3 |
| 2 | 89.6 | 91.0 |
| 3 | 76.6 | 73.6 |
| 4 | 52.2 | 58.2 |
| 5 | 110.8 | 104.2 |
| 6 | 50.4 | 49.9 |
| 7 | 72.4 | 82.1 |
| 8 | 141.4 | 154.1 |
| 9 | 75.0 | 73.4 |
| 10 | 34.1 | 38.1 |
| 11 | 60.3 | 60.1 |
Чи є суттєва різниця між методами при\(\alpha = 0.05\)?
Рішення
Придбання зразків протягом тривалого періоду часу вводить значну залежну від часу зміну концентрації монензину. Оскільки варіація концентрації між зразками настільки велика, ми використовуємо парний t -тест з наступними нульовими та альтернативними гіпотезами.
\[H_0 \text{: } \overline{d} = 0 \quad \quad \quad H_A \text{: } \overline{d} \neq 0 \nonumber\]
Визначення різниці між методами як
\[d_i = (X_\text{elect})_i - (X_\text{micro})_i \nonumber\]
обчислюємо різницю для кожного зразка.
| зразок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| \(d_i\) | 2.8 | 1.4 | —3.0 | 6.0 | —6.6 | —0,5 | 9.7 | 12,7 | —1.6 | 4.0 | —0,2 |
Середнє і стандартне відхилення для відмінностей складають відповідно 2,25 ppt і 5.63 ppt. Значення t exp дорівнює
\[t_\text{exp} = \frac {|2.25| \sqrt{11}} {5.63} = 1.33 \nonumber\]
що менше критичного значення 2,23 для t (0,05, 10) з додатка 2. Ми зберігаємо нульову гіпотезу і не знаходимо доказів істотної різниці в методах на\(\alpha = 0.05\).
Однією з важливих вимог до парного t -тесту є те, що детермінантні та невизначені помилки, які впливають на аналіз, повинні бути незалежними від концентрації аналіта. Якщо це не так, то проба з незвично високою концентрацією аналіту матиме незвично великий d i. Включення цієї вибірки в розрахунок\(\overline{d}\) і s d дає упереджену оцінку для очікуваного середнього і стандартного відхилення. Це рідко є проблемою для зразків, які охоплюють обмежений діапазон концентрацій аналітів, таких як у прикладі\(\PageIndex{4}\) або вправи\(\PageIndex{6}\). Коли парні дані охоплюють широкий діапазон концентрацій, однак, величина детермінантних і невизначений джерел похибки не може бути незалежною від концентрації аналіта; коли це правда, парний t -тест може дати оманливі результати, оскільки парні дані з найбільшим абсолютним домінують визначальні та невизначені помилки\(\overline{d}\). У цій ситуації регресійний аналіз, який є предметом наступної глави, є більш підходящим методом порівняння даних.
Важливість розрізнення парних і непарних даних варто вивчити уважніше. Нижче наведені дані з деякої роботи, яку я завершив з колегою, в якій ми розглядали концентрацію Zn в озері Ері на інтерфейсі повітря-вода та інтерфейс осадок-вода.
| зразок сайту | ppm Zn і інтерфейс повітря-вода | ppm Zn на межі межі осадо-вода |
| 1 | 0,430 | 0,415 |
| 2 | 0,266 | 0,238 |
| 3 | 0,457 | 0,390 |
| 4 | 0.531 | 0,410 |
| 5 | 0,707 | 0.605 |
| 6 | 0,716 | 0,609 |
Середнє значення і стандартне відхилення для ppm Zn на межі розділу повітря-вода становлять 0,5178 ppm і 0,01732 ppm, а середнє і стандартне відхилення для ppm Zn на межі осадок-вода складають 0,4445 ppm і 0,1418 ppm. Ми можемо використовувати ці значення, щоб намалювати нормальні розподіли як для відпускаючи середні та стандартні відхилення для вибірки, так\(\overline{X}\) і\(s\), служити оцінками для засобів і стандартних відхилень для популяції,\(\mu\) і\(\sigma\). Як ми бачимо на наступному малюнку
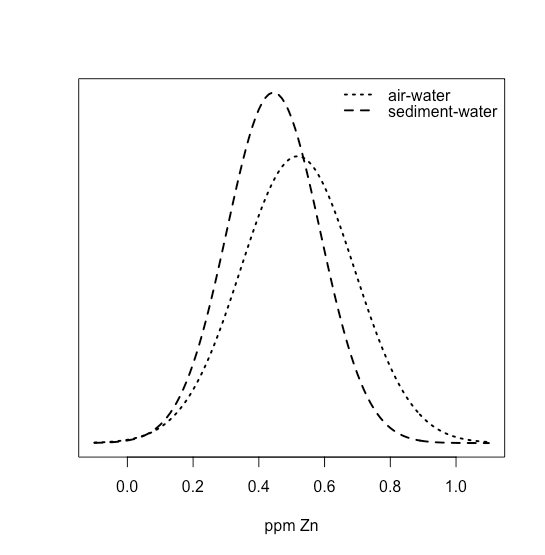
два розподіли сильно перекриваються, припускаючи, що t -тест їх засобів навряд чи знайде докази різниці. І все ж, ми також бачимо, що для кожної ділянки концентрація Zn на межі осаду - вода менше, ніж на межі розділу повітря-вода. При цьому різниця між концентрацією Zn на окремих ділянках досить велика, що маскує нашу здатність бачити різницю між двома інтерфейсами.
Якщо взяти відмінності між інтерфейсами «повітря-вода» і «осад - вода», то маємо значення 0,015, 0,028, 0,067, 0,121, 0,102 і 0,107 проміле Zn, із середнім значенням 0,07333 ppm Zn і стандартним відхиленням 0,04410 ppm Zn. Накладення всіх трьох нормальних розподілів
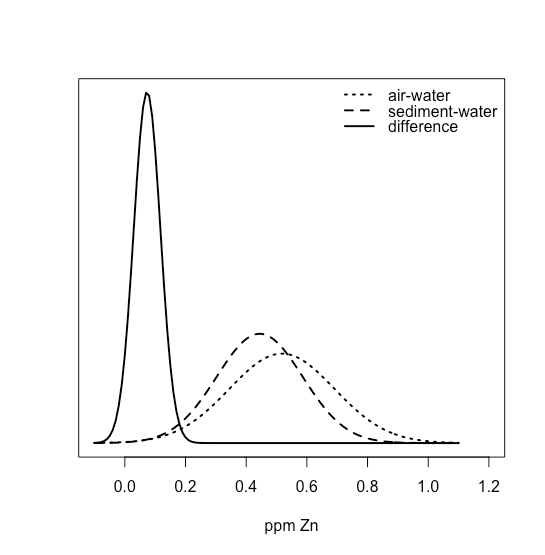
показує чітко, що більша частина нормального розподілу відмінностей лежить вище нуля, припускаючи, що t -тест може показати докази того, що різниця є значною.
Виділення
У розділі 7.1 ми розглянули набір даних, що складається з маси 100 циркулюючих США копійки. Таблиця\(\PageIndex{1}\) надає ще один набір даних. Ви помічаєте щось незвичайне в цих даних? З 100 копійок, включених в більш ранню таблицю, жоден пенні не має маси менше 3 м В цій таблиці, однак маса однієї копійки менше 3 м Ми могли б запитати, чи настільки відрізняється ця маса копійки від інших копійок, що вона помилкова.
| 3.067 | 2.514 | 3.094 |
| 3.049 | 3.048 | 3.109 |
| 3.039 | 3.079 | 3.102 |
Вимірювання, яке не відповідає іншим вимірам, називається викидом. Викид може існувати з багатьох причин: викид може належати іншій популяції
Це канадська копійка?
або викид може бути забрудненим або іншим чином зміненим зразком
Копійка пошкоджена або незвично брудна?
або викид може бути наслідком помилки в аналізі
Ми забули тарувати залишок?
Незалежно від його джерела, наявність викидів компрометує будь-який змістовний аналіз наших даних. Є багато значущих тестів, які ми можемо використовувати для виявлення потенційних викидів, три з яких ми представляємо тут.
Q -Тест Діксона
Одним з найпоширеніших тестів значущості для виявлення викидів є Q-тест Діксона. Нульова гіпотеза полягає в тому, що немає викидів, а альтернативна гіпотеза полягає в тому, що існує викид. Q -тест порівнює розрив між підозрюваним викидом і його найближчим числовим сусідом з діапазоном всього набору даних (рис.\(\PageIndex{2}\)).
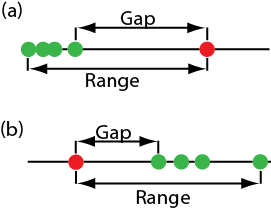
Статистика тесту, Q exp, становить
\[Q_\text{exp} = \frac {\text{gap}} {\text{range}} = \frac {|\text{outlier's value} - \text{nearest value}|} {\text{largest value} - \text{smallest value}} \nonumber\]
Це рівняння підходить для оцінки одного викиду. Інші форми Q -тесту Діксона дозволяють його розширення для виявлення декількох викидів [Rorabacher, D.B. анал. Хім. 1991, 63, 139—146].
Значення Q exp порівнюється з критичним значенням\(Q(\alpha, n)\), де\(\alpha\) є ймовірність того, що ми відхилимо допустиму точку даних (помилка типу 1) і n - загальна кількість точок даних. Щоб захистити від відхилення дійсної точки даних, зазвичай ми застосовуємо більш консервативний двоххвостий Q-тест, хоча можливий викид є найменшим або найбільшим значенням у наборі даних. Якщо Q exp більше\(Q(\alpha, n)\), то ми відхиляємо нульову гіпотезу і можемо виключити викиди. Ми зберігаємо можливий викид, коли Q exp менше або дорівнює\(Q(\alpha, n)\). Таблиця\(\PageIndex{2}\) містить значення\(Q(\alpha, n)\) для набору даних, який має 3—10 значень. Більш велика таблиця знаходиться в додатку 4. Значення для\(Q(\alpha, n)\) припускають базовий нормальний розподіл.
| п | Q (0,05, н) |
|---|---|
| 3 | 0,970 |
| 4 | 0,829 |
| 5 | 0,710 |
| 6 | 0,625 |
| 7 | 0.568 |
| 8 | 0.526 |
| 9 | 0,493 |
| 10 | 0,466 |
Тест Грубба
Хоча Q -тест Діксона є загальним методом оцінки викидів, він більше не підтримується Міжнародною організацією зі стандартизації (ISO), яка рекомендує тест Грубба. Існує кілька версій тесту Грубба в залежності від кількості потенційних викидів. Тут ми розглянемо випадок, коли є єдиний підозрюваний викид.
Детальніше про цю рекомендацію див. Міжнародні стандарти ISO Guide 5752-2 «Точність (правдивість і точність) методів вимірювання та результатів - частина 2: основні методи визначення повторюваності та відтворюваності стандартного методу вимірювання» 1994.
Статистика тесту для тесту Грубба, G exp, - це відстань між середнім значенням зразка та потенційним викидом\(X_\text{out}\), з точки зору стандартного відхилення зразка, с.\(\overline{X}\)
\[G_\text{exp} = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber\]
Порівнюємо значення G exp з критичним значенням\(G(\alpha, n)\), де\(\alpha\) є ймовірність того, що ми відхилимо дійсну точку даних, а n - кількість точок даних у вибірці. Якщо G exp більше\(G(\alpha, n)\), то ми можемо відхилити точку даних як викид, інакше ми збережемо точку даних як частину вибірки. Таблиця\(\PageIndex{3}\) містить значення G (0,05, n) для зразка, що містить 3—10 значень. Більш велика таблиця знаходиться в Додатку 5. Значення для\(G(\alpha, n)\) припускають базовий нормальний розподіл.
| п | Г (0,05, н) |
|---|---|
| 3 | 1,115 |
| 4 | 1.481 |
| 5 | 1.715 |
| 6 | 1.887 |
| 7 | 2.020 |
| 8 | 2.126 |
| 9 | 2.215 |
| 10 | 2.290 |
Критерій Шовене
Наш остаточний метод виявлення викиду - критерій Шовене. На відміну від Q -Test Діксона та тесту Грубба, ви можете застосувати цей метод до будь-якого розподілу, якщо ви знаєте, як обчислити ймовірність для конкретного результату. Критерій Шовене стверджує, що ми можемо відхилити точку даних, якщо ймовірність отримання значення точки даних менше\((2n^{-1})\), де n - розмір вибірки. Наприклад, якщо n = 10, результат з ймовірністю менше\((2 \times 10)^{-1}\), або 0,05, вважається викидом.
Для обчислення ймовірності потенційного викиду спочатку обчислимо його стандартизоване відхилення, z
\[z = \frac {|X_\text{out} - \overline{X}|} {s} \nonumber\]
де\(X_\text{out}\) потенційний викид,\(\overline{X}\) - середнє значення зразка, а s - стандартне відхилення зразка. Зауважте, що це рівняння ідентично рівнянню для G exp у тесті Грубба. Для нормального розподілу можна знайти ймовірність отримання значення z за допомогою таблиці ймовірностей в Додатку 1.
Таблиця\(\PageIndex{1}\) містить маси за дев'ять циркулюючих США копійки. Один запис, 2,514 г, здається, є викидом. Визначте, чи є цей пенні викидом, використовуючи Q -тест, тест Грубба та критерій Шовене. Для Q -тесту та тесту Grubb давайте\(\alpha = 0.05\).
Рішення
Для Q -тесту значення для\(Q_\text{exp}\) дорівнює
\[Q_\text{exp} = \frac {|2.514 - 3.039|} {3.109 - 2.514} = 0.882 \nonumber\]
З таблиці\(\PageIndex{2}\) критичне значення для Q (0,05, 9) дорівнює 0,493. Оскільки Q exp більше Q (0,05, 9), ми можемо припустити, що копійка з масою 2,514 г, ймовірно, є викидом.
Для тесту Грубба спочатку потрібні середнє значення і стандартне відхилення, які складають 3,011 г і 0,188 г відповідно. Значення для G exp дорівнює
\[G_\text{exp} = \frac {|2.514 - 3.011|} {0.188} = 2.64 \nonumber\]
Використовуючи Таблицю\(\PageIndex{3}\), знаходимо, що критичне значення для G (0,05, 9) дорівнює 2,215. Оскільки G exp більше G (0,05, 9), можна припустити, що копійка з масою 2,514 г, ймовірно, є викидом.
Для критерію Шовене критична ймовірність дорівнює\((2 \times 9)^{-1}\), або 0,0556. Значення z таке ж, як G exp, або 2,64. Використовуючи додаток 1, ймовірність для z = 2.64 дорівнює 0,00415. Оскільки ймовірність отримання маси 0,2514 г менше критичної ймовірності, можна припустити, що копійка з масою 2,514 г, швидше за все, є викидом.
Ви повинні проявляти обережність при використанні тесту на значущість для викидів, оскільки є ймовірність, що ви відхилите дійсний результат. Крім того, слід уникати відхилення викиду, якщо це призводить до точності, яка набагато краща, ніж очікувалося, на основі поширення невизначеності. Враховуючи ці побоювання, не дивно, що деякі статистики застерігають проти видалення викидів [Демінг, У.Е. Статистичний аналіз даних; Wiley: Нью-Йорк, 1943 (перевидано Dover: Нью-Йорк, 1961); стор. 171].
Ви також можете прийняти більш сувору вимогу щодо відхилення даних. Наприклад, при використанні тесту Грубба, настанови ISO 5752 пропонують зберегти значення, якщо ймовірність відхилення його більше\(\alpha = 0.05\), ніж, і позначити значення як «відсторонювач», якщо ймовірність відхилення від нього знаходиться між\(\alpha = 0.05\) і\(\alpha = 0.01\). «Відхилення» зберігається, якщо немає вагомих причин для його відхилення. Керівні принципи рекомендують використовувати\(\alpha = 0.01\) як мінімальний критерій для відхилення можливого викиду.
З іншого боку, тестування на викиди може надати корисну інформацію, якщо ми спробуємо зрозуміти джерело підозрюваного викиду. Наприклад, викид в таблиці\(\PageIndex{1}\) являє собою значну зміну маси копійки (приблизно на 17% зменшення маси), що є результатом зміни складу американського пенні. У 1982 році склад американського пенні змінився з латунного сплаву, який становив 95% w/w Cu і 5% w/w Zn (з номінальною масою 3,1 г), до чистого цинкового сердечника, покритого міддю (номінальною масою 2,5 г) [Richardson, T.H. J. chem. Едук. 1991, 68, 310—311]. Копійки в таблиці\(\PageIndex{1}\), таким чином, були залучені з різних популяцій.