5.2: Теоретичні моделі розподілу даних
- Page ID
- 17656
Існує чотири важливі типи розподілів, які ми розглянемо в цьому розділі: рівномірний розподіл, біноміальний розподіл, розподіл Пуассона та нормальний, або Гауссоновий, розподіл. У главі 3 та главі 4 ми використовували аналіз мішків M&Ms для вивчення способів візуалізації даних та узагальнення даних. Тут ми будемо використовувати той самий набір даних для вивчення розподілу даних.
Рівномірний розподіл
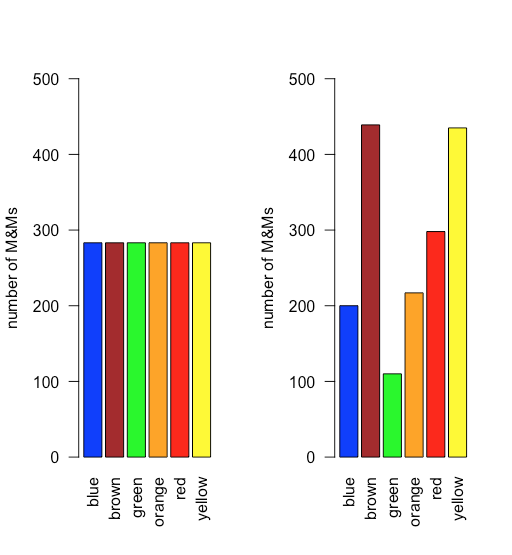
При рівномірному розподілі всі результати однаково вірогідні. Припустимо, населення M&Ms має рівномірний розподіл. Якщо це так, то з шістьма кольорами ми очікуємо, що кожен колір з'явиться з ймовірністю 1/6 або 16,7%. \(\PageIndex{1}\)На малюнку показано порівняння теоретичних результатів, якщо ми намалюємо 1699 M&Ms - загальна кількість M & Ms у нашій вибірці з 30 мішків - від популяції з рівномірним розподілом (зліва) до фактичного розподілу 1699 M&Ms у нашому зразку (праворуч). Здається малоймовірним, що населення M&Ms має рівномірний розподіл кольорів!
Біноміальний розподіл
Біноміальний розподіл показує ймовірність отримання певного результату у фіксованій кількості випробувань, де відомі шанси того результату, що відбувається в одному дослідженні. Математично біноміальний розподіл визначається рівнянням
\[P(X, N) = \frac {N!} {X! (N - X)!} \times p^{X} \times (1 - p)^{N - X} \nonumber\]
де P (X, N) - ймовірність того, що подія відбудеться X разів у N випробуваннях, а де p - ймовірність того, що подія відбудеться в одному дослідженні. Біноміальний розподіл має теоретичне середнє\(\mu\), і теоретичну\(\sigma^2\) дисперсію,
\[\mu = Np \quad \quad \quad \sigma^2 = Np(1 - p) \nonumber\]
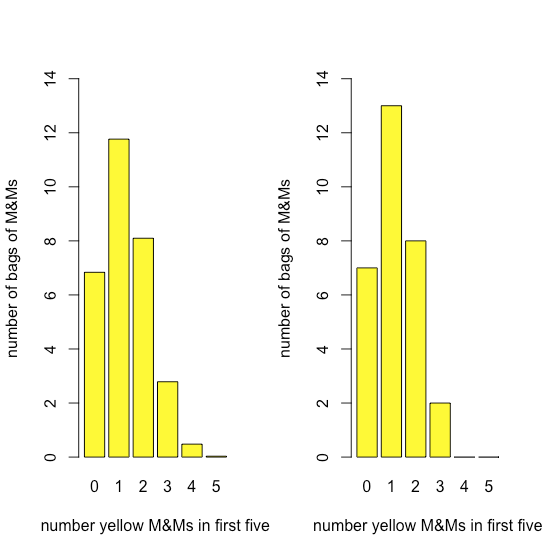
Рисунок\(\PageIndex{2}\) порівнює очікуваний біноміальний розподіл для малювання 0, 1, 2, 3, 4 або 5 жовтих M & Ms у перших п'яти M&MS - припускаючи, що ймовірність нанесення жовтого M & M становить 435/1699, співвідношення кількості жовтих M & Ms та загальної кількості M & MS - до фактичного розподілу результати. Подібність між теоретичними та фактичними результатами здається очевидною; у розділі 6 ми розглянемо способи перевірки цього твердження.
Розподіл Пуассона
Біноміальний розподіл корисний, якщо ми хочемо змоделювати ймовірність знаходження фіксованої кількості жовтих M & Ms у вибірці M & Ms фіксованого розміру - таких як перші п'ять M & Ms, які ми витягуємо з мішка, але не ймовірність знайти фіксовану кількість жовтих M & Ms в одній сумці, оскільки є деяка мінливість у загальній кількості M & Ms на мішок.
Розподіл Пуассона дає ймовірність того, що задана кількість подій відбудеться за фіксований проміжок часу або простору, якщо подія має відомий середній показник і якщо кожна нова подія не залежить від попередньої події. Математично розподіл Пуассона визначається рівнянням
\[P(X, \lambda) = \frac {e^{-\lambda} \lambda^X} {X !} \nonumber\]
де\(P(X, \lambda)\) - ймовірність того, що подія трапиться X разів, враховуючи середню швидкість події,\(\lambda\). Розподіл Пуассона має\(\mu\) теоретичне середнє значення та теоретичну дисперсію\(\sigma^2\), які кожен дорівнює\(\lambda\).
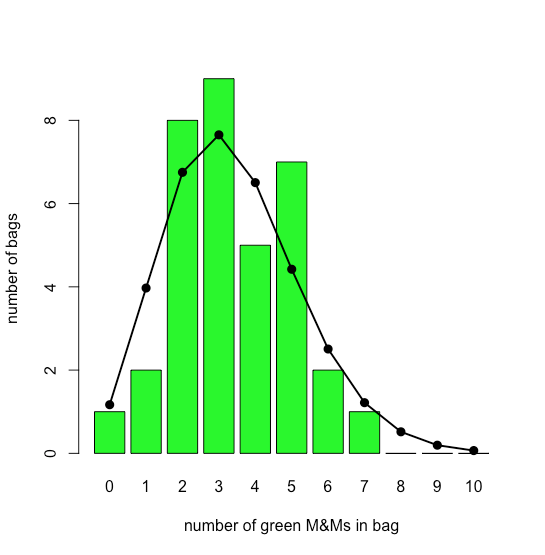
Графік бару на малюнку\(\PageIndex{3}\) показує фактичний розподіл зелених M & Ms у 35 маленьких мішках M&Ms (як повідомляє М.А. Сю-Фрідман «Ілюстрація концепцій квантового аналізу з інтуїтивною моделлю класу», адв. Physiol. Едук. 2013, 37, 112—116). На смугу накладається теоретичний розподіл Пуассона, заснований на їх повідомленій середній швидкості 3.4 зелених M & Ms за мішок. Подібність між теоретичними та фактичними результатами здається очевидною; у розділі 6 ми розглянемо способи перевірки цього твердження.
Нормальний розподіл
Рівномірний розподіл, біноміальний розподіл та розподіл Пуассона прогнозують ймовірність дискретної події, такої як ймовірність знаходження рівно двох зелених M&Ms у наступному мішку M&Ms, який ми відкриваємо. Не всі дані, які ми збираємо, є дискретними. Вага нетто мішків M&Ms є прикладом безперервних даних, оскільки маса окремого мішка не обмежується дискретним набором дозволених значень. У багатьох випадках ми можемо моделювати неперервні дані за допомогою нормального (або гаусового) розподілу, що дає ймовірність отримання певного результату, P (x), від популяції з відомим середнім значенням та відомою дисперсією\(\sigma^2\).\(\mu\) Математично нормальний розподіл визначається рівнянням
\[P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber\]
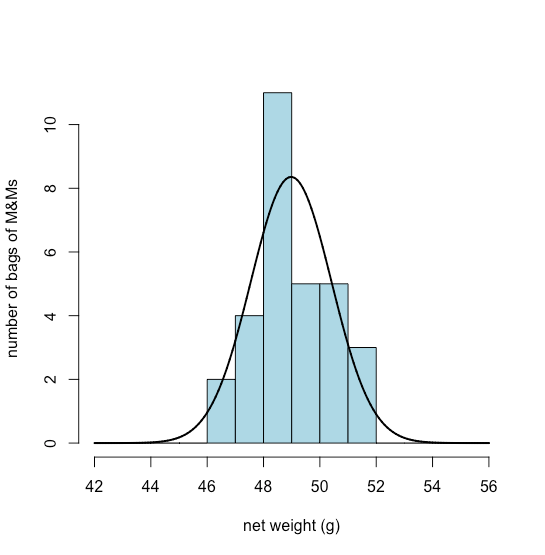
\(\PageIndex{4}\)На малюнку показано очікуваний нормальний розподіл ваги нетто нашої вибірки з 30 мішків M & Ms, якщо припустити\(\overline{X}\), що їх середнє значення 48,98 г і стандартне відхилення, с, 1.433 г є хорошими предикторами середнього показника популяції та стандартного відхилення,\(\mu\) \(\sigma\). Враховуючи невеликий зразок із 30 мішків, угода між моделлю та даними здається розумною.