16.2: Поширення невизначеності
- Page ID
- 24876
У розділі 4 ми розглянули основні математичні деталі поширення невизначеності, обмежуючи наше лікування поширенням похибки вимірювання. Це лікування є неповним, оскільки воно пропускає інші джерела невизначеності, які сприяють загальній невизначеності наших результатів. Розглянемо, наприклад, вправу 4.3.1, в якому ми визначили невизначеність в стандартному розчині Cu 2 +, приготованому розчиненням відомої маси дроту Cu з HNO 3, розведенням до обсягу в об'ємній колбі об'ємом 500 мл, а потім розведенням 1-мл цієї порції запас розчину до обсягу в об'ємній колбі об'ємом 250 мл. Для розрахунку загальної невизначеності ми включили невизначеність при зважуванні зразка та невизначеність використання об'ємного скляного посуду. Ми не розглядали інших джерел невизначеності, включаючи чистоту дроту Cu, вплив температури на об'ємний скляний посуд, повторюваність наших вимірювань. У цьому додатку ми детальніше розглянемо поширення невизначеності, використовуючи стандартизацію NaOH як приклад.
Стандартизація рішення NaOH
Оскільки твердий NaOH є нечистим матеріалом, ми не можемо безпосередньо приготувати запасний розчин, зважуючи зразок NaOH та розбавляючи до об'єму. Натомість ми визначаємо концентрацію розчину за допомогою процесу, який називається стандартизацією. Досить типовою процедурою є використання розчину NaOH для титрування ретельно зваженого зразка раніше висушеного фталату водню калію, C 8 H 5 O 4 K, який ми напишемо тут, в скороченому вигляді, як КХП. Наприклад, після приготування номінально 0,1 М розчину NaOH поміщаємо точно зважений 0,4-г зразок висушеного КХП в реакційну ємність автоматизованого титратора і розчиняємо його приблизно в 50 мл води (точна кількість води не важливо). Автоматизований титратор додає NaOH до розчину КХП і записує рН як функцію обсягу NaOH. Отримана крива титрування забезпечує нам обсяг NaOH, необхідний для досягнення кінцевої точки титрування.
Приклад нижче адаптований з Еллісона, С.Л. Р.; Росслійн, М.; Вільямс, A. EURACHEM/CITAC Керівництво: Кількісна оцінка невизначеності в аналітичних вимірах, 3-е видання, 2012. Див. Розділ 5 для отримання додаткової інформації про стандартизацію та див. Розділ 9 для отримання детальної інформації про титрування.
Кінцевою точкою титрування є обсяг NaOH, який відповідає стехіометричної реакції між NaOH і KHP.
\[\ce{NaOH}(aq) + \ce{C8H5O4K}(aq) \ce{->} \ce{C8H4O4^{2-}}(aq) + \ce{K+}(aq) + \ce{Na+}(aq) + \ce{H2O}(l) \nonumber\]
Знаючи масу КХП і обсяг NaOH, необхідний для досягнення кінцевої точки, використовуємо наступне рівняння для обчислення молярності розчину NaOH.
\[C_\ce{NaOH} = \frac {1000 \times m_\ce{KHP} \times P_\ce{KHP}} {FW_\ce{KHP} \times V_\ce{NaOH}} \nonumber\]
де С NaOH - концентрація NaOH (в моль КХП/Л), м КХП - маса взятої КХП (в г), Р КХП - чистота КХП (де Р КХП = 1 означає КХП чистий і не має домішок), FW КХП - молярна маса КХП (в г КХП/моль КХП), а V NaOH - обсяг NaOH (в мл). Коефіцієнт 1000 просто перетворює обсяг в мл в L.
Виявлення та аналіз джерел невизначеності
Хоча це здається простим, виявлення джерел невизначеності вимагає обережності, оскільки легко не помітити важливі джерела невизначеності. Один з підходів полягає у використанні причинно-наслідкової діаграми, також відомої як діаграма Ісікава, названа на честь свого винахідника, Каору Ісікава - або діаграми риб'ячої кістки. Для побудови причинно-наслідкової діаграми спочатку намалюємо стрілку, яка вказує на бажаний результат; це стовбур діаграми. Потім ми додаємо п'ять основних гілок до стовбура, по одній для кожного з чотирьох параметрів, що визначають концентрацію NaOH (m KHP, P KHP, FW KHP та V NaOH) і по одному для повторюваності методу, Р. Далі ми додаємо додаткові гілки до основної гілки для кожного з цих п'яти факторів, продовжуючи до тих пір, поки не врахуємо всі потенційні джерела невизначеності. На малюнку Template:index показано повну причинно-наслідкову діаграму для цього аналізу.
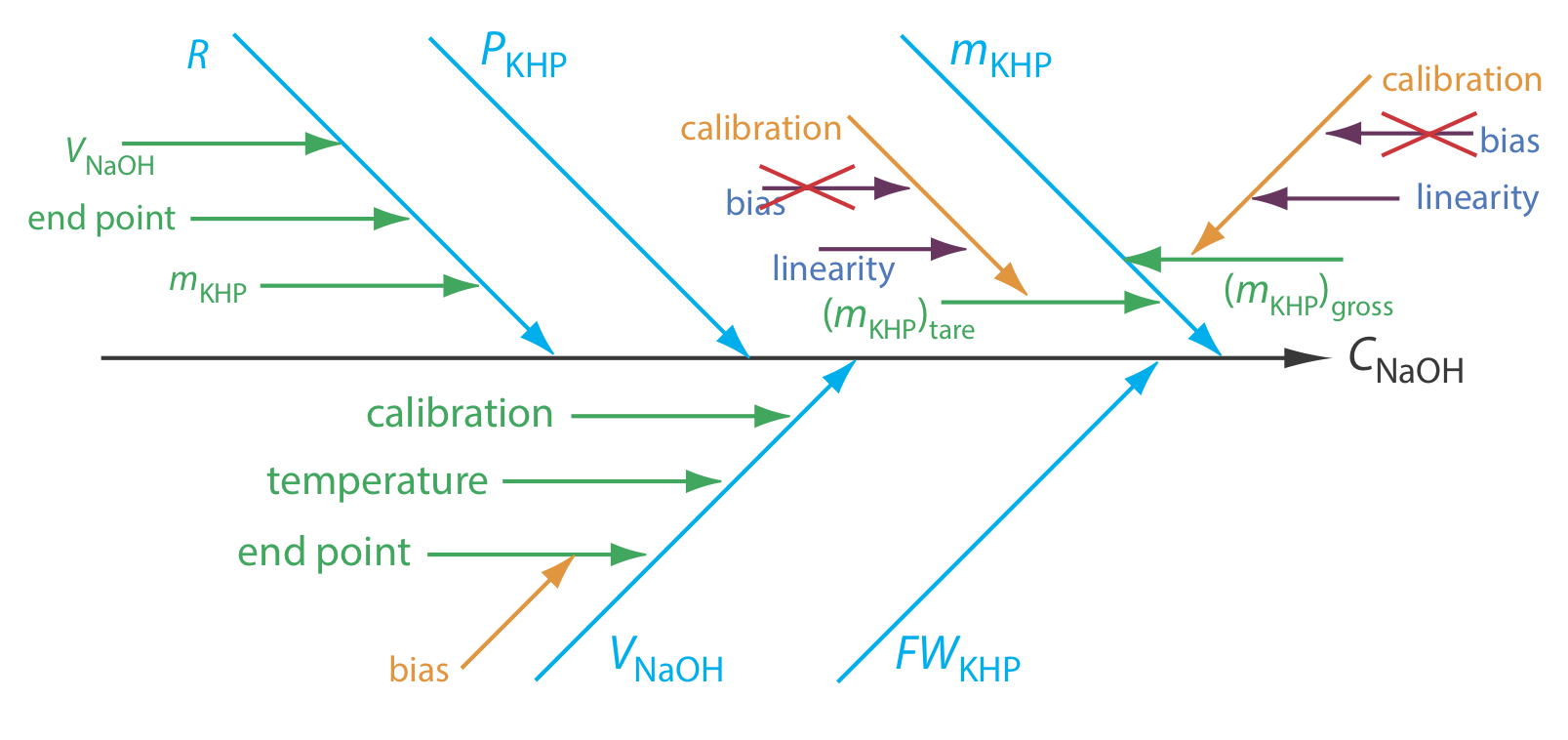
Перш ніж продовжити, давайте детальніше розглянемо Figure Template:index, щоб переконатися, що ми розуміємо кожну гілку діаграми. Для визначення маси КХП, м КХП проводимо два виміри: таринг ваги і зважування брутто проби. Кожне з цих вимірювань підлягає калібрувальній невизначеності. Коли ми калібруємо баланс, ми по суті створюємо калібрувальну криву сигналу балансу як функції маси. Будь-яка калібрувальна крива піддається невизначеності у -перехопленні (зміщення) та невизначеності нахилу (лінійності). Ми можемо ігнорувати калібрувальний ухил, оскільки він однаково сприяє як (м КХП) брутто, так і (м КХП) тари, і тому, що ми визначаємо масу КХП по різниці.
\[m_\ce{KHP} = \left( m_\ce{KHP} \right)_\text{gross} - \left( m_\ce{KHP} \right)_\text{tare} \nonumber\]
Обсяг NaOH, V NaOH, в кінцевій точці має три джерела невизначеності. По-перше, автоматизований титратор використовує поршень для доставки NaOH до реакційної посудини, що означає, що обсяг NaOH піддається невизначеності калібрування поршня. По-друге, оскільки обсяг розчину змінюється залежно від температури, виникає додаткове джерело невизначеності через будь-які коливання температури навколишнього середовища під час аналізу. Нарешті, існує зміщення кінцевої точки титрування, якщо NaOH реагує з будь-якими видами, крім КХП.
Повторюваність, R, є мірою того, наскільки послідовно ми можемо повторити аналіз. Кожен інструмент, який ми використовуємо - баланс і автоматизований титратор - сприяє цій невизначеності. Крім того, наша здатність послідовно виявляти кінцеву точку також сприяє повторюваності. Нарешті, немає вторинних факторів, які впливають на невизначеність чистоти КХП, П КХП, або його молярної маси, ФВ КХП.
Оцінка стандартного відхилення для вимірювань
Щоб завершити поширення невизначеності, ми повинні виразити невизначеність кожного вимірювання так само, як правило, як стандартне відхилення. Вимірювання стандартного відхилення для кожного вимірювання вимагає часу і не завжди є практичним. На щастя, більшість виробників забезпечує діапазон допусків для скляного посуду та інструментів. Наприклад, об'ємний скляний посуд об'ємом 100 мл має допуск\(\pm 0.1 \text{ mL}\) при температурі 20 o С. Ми можемо перетворити діапазон допуску в стандартне відхилення, використовуючи один з наступних трьох підходів.
Припустимо рівномірний розподіл
Рисунок Template:index a показує рівномірний розподіл між межами\(\pm x\), при якому кожен результат між межами однаково вірогідний. Рівномірний розподіл - це вибір, коли виробник забезпечує діапазон допуску без вказівки рівня довіри і коли немає підстав вважати, що результати поблизу центру діапазону є більш імовірними, ніж результати на кінцях діапазону. Для рівномірного розподілу розрахункове стандартне відхилення, s, дорівнює
\[s = \frac {x} {\sqrt{3}} \nonumber\]
Це найбільш консервативна оцінка невизначеності, оскільки вона дає найбільшу оцінку стандартного відхилення.

Припустимо трикутний розподіл
На рисунку Template:index b показано трикутний розподіл між межами\(\pm x\), в якому найбільш ймовірний результат знаходиться в центрі розподілу, лінійно зменшується до кожної межі. Трикутний розподіл - це вибір, коли виробник забезпечує діапазон допуску без вказівки рівня довіри і коли є вагомі підстави вважати, що результати поблизу центру діапазону є більш імовірними, ніж результати на кінцях діапазону. Для трикутного розподілу розрахункове стандартне відхилення, s, дорівнює
\[s = \frac {x} {\sqrt{6}} \nonumber\]
Це менш консервативна оцінка невизначеності, оскільки для будь-якого значення x стандартне відхилення менше, ніж для рівномірного розподілу.
Припустімо нормальний розподіл
Рисунок Template:index c показує нормальний розподіл, який, як треба\(\pm x\), виходить за межі, і який знаходиться в центрі між — x і + x. Нормальний розподіл - це вибір, коли ми знаємо довірчий інтервал для діапазону. Для нормального розподілу розрахункове стандартне відхилення, с, дорівнює
\[s = \frac {x} {z} \nonumber\]
де z дорівнює 1.96 для 95% довірчого інтервалу і 3.00 для довірчого інтервалу 99,7%.
Завершення поширення невизначеності
Тепер ми готові повернутися до нашого прикладу і визначити невизначеність для стандартизації NaOH. Спочатку встановлено невизначеність для кожного з п'яти первинних джерел - маса КХП, об'єм NaOH в кінцевій точці, чистота КХП, молярна маса для КХП та повторюваність титрування. Встановивши їх, ми можемо об'єднати їх, щоб досягти остаточної невизначеності.
Невизначеність маси КХП
Після висихання КХП зберігаємо його в герметичній тарі, щоб він не засвоював вологу. Для знаходження маси КХП спочатку зважуємо тару, отримуючи значення 60,5450 г, а потім зважуємо тару після зняття частини КХП, отримавши значення 60,1562 м Маса КХП, отже, становить 60,5450 — 60.1562 = 0,3888 г, або 388,8 мг.
Щоб знайти невизначеність у цій масі, ми вивчаємо сертифікат калібрування балансу, який вказує на його допуск до лінійності\(\pm 0.15 \text{ mg}\). Ми будемо вважати рівномірний розподіл, оскільки немає підстав вважати, що будь-який результат у цьому діапазоні є більш імовірним, ніж будь-який інший результат. Наша оцінка невизначеності для будь-якого єдиного вимірювання маси, u (м), становить
\[u(m) = \frac {0.15 \text{ mg}} {\sqrt{3}} = \pm 0.087 \text{ mg} \nonumber\]
Оскільки ми визначаємо масу КХП шляхом віднімання кінцевої маси контейнера від його початкової маси, невизначеність в масі КХП u (м КХП) задається наступним поширенням невизначеності.
\[u(m_{\text{KHP}}) = \sqrt{\left( 0.087 \text{ mg} \right)^2 + \left( 0.087 \text{ mg} \right)^2} =\pm 0.12 \text{ mg} \nonumber\]
Невизначеність в обсязі NaOH
Після того, як ми поміщаємо зразок КХП в реакційну ємність автоматизованого титратора і розчиняємо КХП водою, ми завершуємо титрування і виявляємо, що для досягнення кінцевої точки потрібно 18,64 мл NaOH. Щоб знайти невизначеність у цьому обсязі, нам потрібно врахувати, як показано на рисунку Template:index, три джерела невизначеності: автоматизоване калібрування титратора, температуру навколишнього середовища та будь-який ухил при визначенні кінцевої точки.
Щоб знайти невизначеність від калібрування автоматизованого титратора, ми вивчаємо сертифікат приладу, який вказує діапазон\(\pm 0.03 \text{ mL}\) для 20-мл поршня. Оскільки ми очікуємо, що ефективний виробничий процес швидше виробляє поршень, який працює поблизу центру цього діапазону, ніж в крайності, ми будемо вважати трикутне розподіл. Наша оцінка невизначеності внаслідок калібрування, u (V cal) дорівнює
\[u(V_\text{cal}) = \frac {0.03 \text{ mL}} {\sqrt{6}} = \pm 0.012 \text{ mL} \nonumber\]
Щоб визначити невизначеність через відсутність контролю температури, ми спираємося на нашу попередню роботу в лабораторії, яка встановила коливання температури\(\pm 3 \text{°C}\) з довірчим рівнем 95%. Для знаходження невизначеності перетворюємо температурний діапазон в діапазон об'ємів, використовуючи коефіцієнт розширення води.
\[(2.1 \times 10^{-4} \text{°C}) \times (\pm 3 \text{°C}) \times 18.64 \text{ mL} = \pm 0.012 \text{ mL} \nonumber\]
а потім оцінити невизначеність через температуру, u (V temp) як
\[u(V_\text{temp}) = \frac {\pm 0.012 \text{ mL}} {1.96} = \pm 0.006 \text{ mL} \nonumber\]
Титрування з використанням NaOH піддаються зміщенню через адсорбцію CO 2, який може реагувати з OH - як показано тут.
\[\ce{CO2}(aq) + \ce{2OH-}(aq) \ce{->} \ce{CO3^{2-}}(aq) + \ce{H2O}(l) \nonumber\]
Якщо присутній СО 2, об'єм NaOH в кінцевій точці включає як NaOH, який реагує з KHP, так і NaOH, який реагує з CO 2. Замість того, щоб намагатися оцінити цей ухил, легше купати реакційну посудину в потоці аргону, який виключає СО 2 з реакційного судини автоматизованого титратора.
Додавання разом невизначеності для калібрування поршня та температури лабораторії дає невизначеність у невизначеності в обсязі NaOH, u (V NaOH) як
\[u(V_\ce{NaOH}) = \sqrt{(0.012 \text{ mL})^2 + (0.006 \text{ mL})^2} = \pm 0.013 \text{ mL} \nonumber\]
Невизначеність в чистоті КХП
За словами виробника, чистота КХП буває\(100 \% \pm 0.05 \%\), або\(1.0 \pm 0.0005\). Припускаючи прямокутний розподіл, ми повідомляємо невизначеність, u (P KHP) як
\[u(P_\ce{KHP}) = \frac {\pm 0.0005} {\sqrt{3}} = \pm 0.00029 \nonumber\]
Невизначеність молярної маси КХП
Молярна маса C 8 H 5 O 4 K становить 204,2212 г/моль, виходячи з наступних атомарних ваг: 12,0107 для вуглецю, 1,00794 для водню, 15,9994 для кисню та 39.0983 для калію. Кожен з цих атомних ваг має лапки невизначеність, яку ми можемо перетворити на стандартну невизначеність, припускаючи прямокутний розподіл, як показано тут (деталі обчислень залишаються вам).
| елемент |
цитується невизначеність (на атом) |
стандартна невизначеність (на атом) |
кількість атомів | повна невизначеність |
|---|---|---|---|---|
| вуглець | \(\pm 0.008\) | \(\pm 0.00046\) | 8 | \(\pm 0.00368\) |
| водню | \(\pm 0.00007\) | \(\ 0.000040\) | 5 | \(\pm 0.00020\) |
| кисень | \(\pm 0.0003\) | \(\pm 0.00017\) | 4 | \(\pm 0.00068\) |
| калій | \(\pm 0.0001\) | \(\pm 0.000058\) | 1 | \(\pm 0.000058\) |
Додавання цих невизначеностей дає невизначеність в молярній масі, u (M KHP), як
\[u(FW_\ce{KHP}) = \sqrt{(0.00368)^2 + (0.00020)^2 + (0.00068)^2 + (0.0.000058)^2} = \pm 0.0037 \text{ g/mL} \nonumber\]
Невизначеність у повторюваності титрування
Для оцінки невизначеності, обумовленої повторюваністю, виконано п'ять титрувань, отримавши наступні результати для концентрації NaOH: 0,1021 М, 0,1022 М, 0,1022 М, 0,1021 М та 0,1021 М. Відносне стандартне відхилення, s rel, для цих титрувань становить
\[s_{rel} = \frac {s} {\overline{X}} = \frac {5.48 \times 10^{-5}} {0.1021} = \pm 0.0005 \nonumber\]
Якщо розглядати ідеальну повторюваність як 1,0, то невизначеність, обумовлена повторюваністю, u (R), є відносним стандартним відхиленням, або, в даному випадку, 0,0005.
Поєднання невизначеностей
Наведена нижче таблиця узагальнює п'ять первинних джерел невизначеності.
| термін | джерело | значення, х | невизначеність, u (x) |
|---|---|---|---|
| \(m_\ce{KHP}\) | маса КХП | 0,3888 г | \(\pm 0.00012\)г |
| \(V_\ce{naOH}\) | обсяг NaOH в кінцевій точці | 18.64 мл | \(\pm 0.013\)мл |
| \(P_\ce{KHP}\) | чистота КХП | 1.0 | \(\pm 0.00029\) |
| \(M_\ce{KHP}\) | молярна маса КХП | 204.2212 г/моль | \(\pm 0.0037\)г/моль |
| \(R\) | повторюваність | 1.0 | \(\pm 0.0005\) |
Як описано раніше, для обчислення концентрації NaOH ми використовуємо наступне рівняння, яке трохи змінено для включення терміна повторюваності титрування, який, як описано вище, має значення 1,0.
\[C_\ce{NaOH} = \frac {1000 \times m_\ce{KHP} \times P_\ce{KHP}} {FW_\ce{KHP} \times V_\ce{NaOH}} \times R \nonumber\]
Використовуючи значення з нашої таблиці, знаходимо, що концентрація NaOH дорівнює
\[C_\ce{NaOH} = \frac {1000 \times 0.3888 \times 1.0} {204.2212 \times 18.64} \times 1.0 = 0.1021 \text{ M} \nonumber\]
Оскільки розрахунок C NaOH включає тільки множення і ділення, невизначеність в концентрації, u (C NaOH) задається наступним поширенням невизначеності.
\[\frac {u(C_\ce{NaOH})} {C_\ce{NaOH}} = \frac {u(C_\ce{NaOH})} {0.1021} = \sqrt{\frac {(0.00012)^2} {(0.3888)^2} + \frac {(0.00029)^2} {(1.0)^2} + \frac {(0.0037)^2} {(204.2212)^2} + \frac {(0.013)^2} {(18.64)^2} + \frac {(0.0005)^2} {(1.0)^2}} \nonumber\]
Розв'язування для u (C NaOH) дає його значення як\(\pm 0.00010 \text{ M}\), що є кінцевою невизначеністю для аналізу.
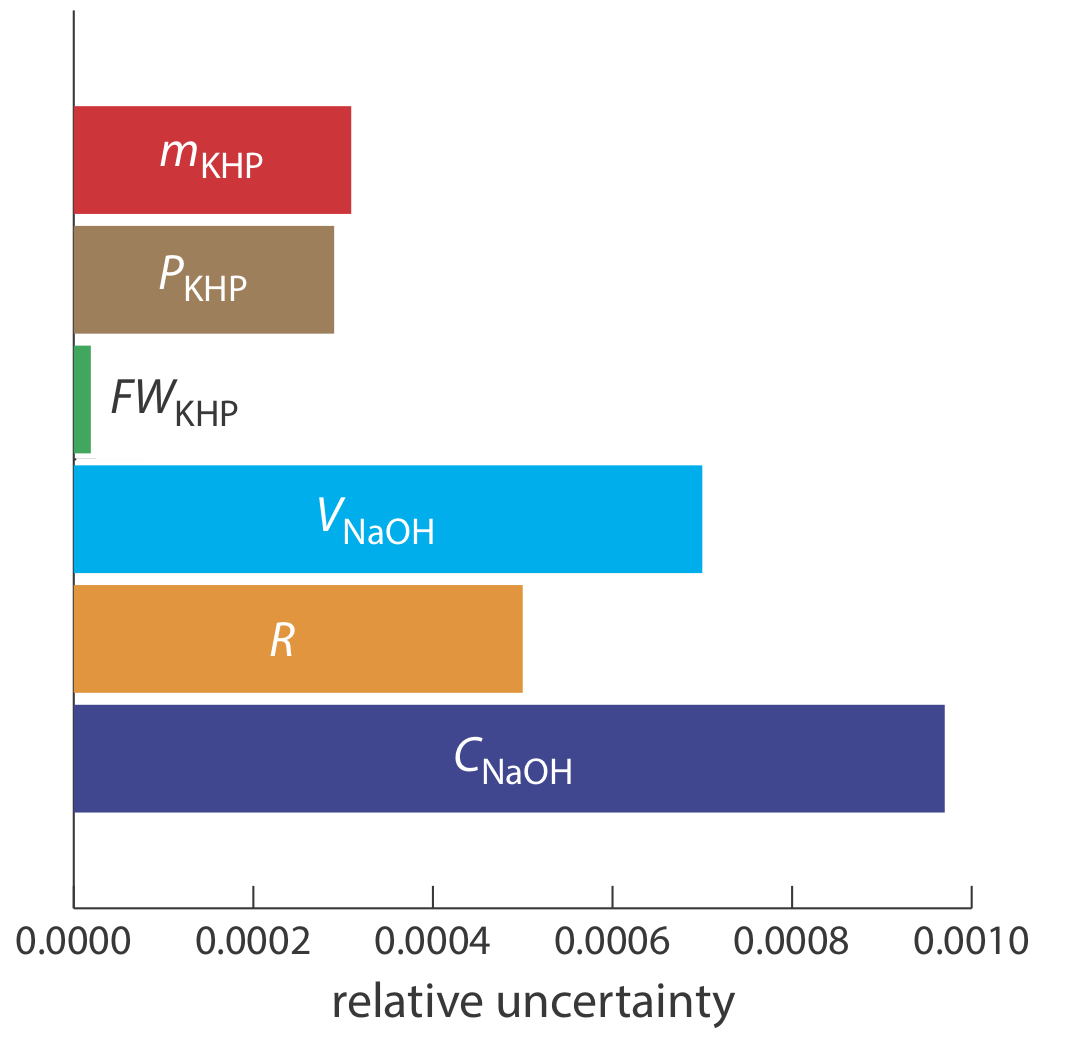
Оцінка джерел невизначеності
Рисунок Template:index показує відносну невизначеність концентрації NaOH та відносну невизначеність для кожного з п'яти внесків у загальну невизначеність. З внесків найважливішим є обсяг NaOH, і саме тут ми повинні зосередити свою увагу, якщо хочемо покращити загальну невизначеність щодо стандартизації.