5.4: Лінійна регресія та калібрувальні криві
- Page ID
- 24954
При одноточковій зовнішній стандартизації визначаємо значення k A шляхом вимірювання сигналу для єдиного стандарту, який містить відому концентрацію аналіту. Використовуючи це значення k A і сигнал нашого зразка, ми потім обчислюємо концентрацію аналіту в нашому зразку (див. Приклад 5.3.1). При єдиному визначенні k A кількісний аналіз з використанням одноточкової зовнішньої стандартизації простий.
Багатоточкова стандартизація представляє більш складну проблему. Розглянемо дані в таблиці Template:index для багатоточкової зовнішньої стандартизації. Яка наша найкраща оцінка співвідношення між S std та C std? Спокусливо розглядати ці дані як п'ять окремих одноточкових стандартизацій, визначаючи k A для кожного стандарту та повідомляючи про середнє значення для п'яти випробувань. Незважаючи на простоту, це не є підходящим способом лікування множинної стандартизації.
| \(C_{std}\)(довільні одиниці) | \(S_{std}\)(довільні одиниці) | \(k_A = S_{std}/C_{std}\) |
|---|---|---|
| \ (C_ {std}\) (довільні одиниці виміру) ">0.000 | \ (S_ {std}\) (довільні одиниці виміру) ">0.00 | \ (K_a = S_ {std} /C_ {std}\) ">— |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.100 | \ (S_ {std}\) (довільні одиниці виміру) ">12.36 | \ (K_a = S_ {std} /C_ {std}\) ">123.6 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.200 | \ (S_ {std}\) (довільні одиниці виміру) ">24.83 | \ (K_a = S_ {std} /C_ {std}\) ">124.2 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.300 | \ (S_ {std}\) (довільні одиниці виміру) ">35.91 | \ (K_a = S_ {std} /C_ {std}\) ">119.7 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.400 | \ (S_ {std}\) (довільні одиниці виміру) ">48.79 | \ (K_a = S_ {std} /C_ {std}\) ">122.0 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.500 | \ (S_ {std}\) (довільні одиниці виміру) ">60.42 | \ (K_a = S_ {std} /C_ {std}\) ">122.8 |
| \ (C_ {std}\) (довільні одиниці)» клас = "lt-chem-132505"> | \ (S_ {std}\) (довільні одиниці виміру) "> | \ (K_a = S_ {std} /C_ {std}\) ">середнє k A = 122,5 |
Так чому ж недоцільно обчислювати середнє значення для k A за допомогою даних у таблиці Template:index? При одноточковій стандартизації ми припускаємо, що порожній реагент (перший рядок у таблиці Template:index) виправляє всі постійні джерела визначеної помилки. Якщо це не так, то значення k A з одноточкової стандартизації має постійну детермінантну похибку. Таблиця Template:index демонструє, як невиправлена постійна помилка впливає на наше визначення k A. Перші три стовпці показують концентрацію аналіту в наборі стандартів, C std, сигнал без будь-якого джерела постійної помилки, S std, і фактичне значення k A протягом п'яти стандарти. Як ми очікуємо, значення k A однакове для кожного стандарту. У четвертому стовпці додаємо постійну детермінантну похибку +0,50 до сигналів, (S std) e. Останній стовпець містить відповідні видимі значення k A. Зауважте, що ми отримуємо різне значення k A для кожного стандарту і що кожне видиме k A більше істинного значення.
| \(C_{std}\) |
\(S_{std}\) |
\(k_A = S_{std}/C_{std}\) |
\((S_{std})_e\) |
\(k_A = (S_{std})_e/C_{std}\) |
|---|---|---|---|---|
| \ (C_ {std}\) ">1.00 | \ (S_ {std}\) (без постійної помилки) ">1.00 | \ (K_a = S_ {std} /C_ {std}\) (фактичний) ">1,00 | \ (S_ {std}) _e\) (з постійною помилкою) ">1.50 | \ (K_a = (S_ {std}) _e/c_ {std}\) (очевидно) ">1.50 |
| \ (C_ {std}\) ">2.00 | \ (S_ {std}\) (без постійної помилки) ">2.00 | \ (K_a = S_ {std} /C_ {std}\) (фактичний) ">1,00 | \ (S_ {std}) _e\) (з постійною помилкою) ">2.50 | \ (K_a = (S_ {std}) _e/c_ {std}\) (очевидно) ">1.25 |
| \ (C_ {std}\) ">3.00 | \ (S_ {std}\) (без постійної помилки) ">3.00 | \ (K_a = S_ {std} /C_ {std}\) (фактичний) ">1,00 | \ ((S_ {std}) _e\) (з постійною помилкою) ">3.50 | \ (K_a = (S_ {std}) _e/c_ {std}\) (очевидно) ">1.17 |
| \ (C_ {std}\) ">4.00 | \ (S_ {std}\) (без постійної помилки) ">4.00 | \ (K_a = S_ {std} /C_ {std}\) (фактичний) ">1,00 | \ (S_ {std}) _e\) (з постійною помилкою) ">4.50 | \ (K_a = (S_ {std}) _e/c_ {std}\) (очевидно) ">1.13 |
| \ (C_ {std}\) ">5.00 | \ (S_ {std}\) (без постійної помилки) ">5.00 | \ (K_a = S_ {std} /C_ {std}\) (фактичний) ">1,00 | \ (S_ {std}) _e\) (з постійною помилкою) ">5.50 | \ (K_a = (S_ {std}) _e/c_ {std}\) (очевидно) ">1.10 |
| \ (C_ {std}\)» клас = "лт-хім-132505"> | \ (S_ {std}\) (без постійної помилки) "> | \ (K_a = S_ {std} /C_ {std}\) (фактичний) ">середнє k A (істинно) = 1,00 | \ (S_ {std}) _e\) (з постійною помилкою) "> | \ (K_a = (S_ {std}) _e/c_ {std}\) (очевидно) ">середнє k A (очевидно) = 1.23 |
Як ми знаходимо найкращу оцінку зв'язку між сигналом та концентрацією аналіту в багатоточковій стандартизації? Рисунок Template:index показує дані в таблиці Template:index, побудованої як звичайна калібрувальна крива. Хоча дані, безумовно, падають по прямій лінії, фактична крива калібрування інтуїтивно не очевидна. Процес визначення найкращого рівняння для калібрувальної кривої називається лінійною регресією.
Лінійна регресія прямолінійних калібрувальних кривих
Коли калібрувальна крива є прямою, ми представляємо її за допомогою наступного математичного рівняння
\[y = \beta_0 + \beta_1 x \label{5.1}\]
де y - сигнал аналіта, S std, а x - концентрація аналіта, C std. Константи\(\beta_0\) і\(\beta_1\) є, відповідно, очікуваним y -перехопленням калібрувальної кривої та очікуваним нахилом. Через невизначеність наших вимірювань найкраще, що ми можемо зробити, це оцінити значення для\(\beta_0\) і\(\beta_1\), які ми представляємо як b 0 і b 1. Метою лінійного регресійного аналізу є визначення найкращих оцінок для b 0 та b 1. Як ми це робимо, залежить від невизначеності наших вимірювань.
Незважена лінійна регресія з помилками у y
Найпоширеніший метод завершення лінійної регресії для Equation\ ref {5.1} робить три припущення:
- що різниця між нашими експериментальними даними та обчисленою лінією регресії є результатом невизначеної помилки, що впливають на y
- що невизначені помилки, які впливають на y, зазвичай розподіляються
- що невизначені похибки в y не залежать від значення x
Оскільки ми припускаємо, що невизначені помилки однакові для всіх стандартів, кожен стандарт однаково вносить свій внесок у нашу оцінку нахилу та y -перехоплення. З цієї причини результат вважається незваженою лінійною регресією.
Друге припущення, як правило, вірно через центральну граничну теорему, яку ми розглянули в главі 4. Обґрунтованість двох інших припущень менш очевидна, і ви повинні оцінити їх, перш ніж приймати результати лінійної регресії. Зокрема, перше припущення завжди є підозрюваним, оскільки, безумовно, є певна невизначена похибка вимірювання x. Коли ми готуємо калібрувальну криву, однак, незвично виявити, що невизначеність у сигналі, S std, значно більша, ніж невизначеність в концентрації аналіта, C std. За таких обставин перше припущення, як правило, є розумним.
Як працює лінійна регресія
Щоб зрозуміти логіку лінійної регресії, розглянемо приклад, показаний на малюнку Template:index, де показано три точки даних і дві можливі прямі лінії, які можуть обґрунтовано пояснити дані. Як ми вирішуємо, наскільки добре ці прямі лінії відповідають даним, і як ми визначаємо найкращу пряму лінію?
Давайте зосередимося на суцільній лінії на малюнку Template:index. Рівняння для цього рядка
\[\hat{y} = b_0 + b_1 x \label{5.2}\]
де b 0 і b 1 - оцінки для y -перехоплення та нахилу, і\(\hat{y}\) є прогнозованим значенням y для будь-якого значення x. Оскільки ми припускаємо, що вся невизначеність є результатом невизначеної помилки у, різниця між y і\(\hat{y}\) для кожного значення x є залишковою похибкою, r, в нашій математичній моделі.
\[r_i = (y_i - \hat{y}_i) \nonumber\]
Рисунок Template:index показує залишкові помилки для трьох точок даних. Чим менше загальна залишкова помилка, R, яку ми визначаємо як
\[R = \sum_{i = 1}^{n} (y_i - \hat{y}_i)^2 \label{5.3}\]
тим краще прилягання між прямою лінією і даними. У лінійному регресійному аналізі ми шукаємо значення b 0 та b 1, які дають найменшу загальну залишкову похибку.
Причина квадратизації окремих залишкових помилок полягає в тому, щоб запобігти позитивній залишковій помилку від скасування негативної залишкової помилки. Ви бачили це раніше в рівняннях для вибірки і популяції стандартних відхилень. З цього рівняння також видно, чому лінійну регресію іноді називають методом найменших квадратів.
Знаходження схилу і y -Перехоплення
Хоча формально ми не будемо розробляти математичні рівняння для лінійного регресійного аналізу, ви можете знайти похідні в багатьох стандартних статистичних текстах [Див., наприклад, Draper, Н.Р.; Smith, H. прикладний регресійний аналіз, 3-е видання; Wiley: Нью-Йорк, 1998]. Отримане рівняння для ухилу, b 1, дорівнює
і рівняння для y -перехоплення, b 0, дорівнює
\[b_0 = \frac {\sum_{i = 1}^{n} y_i - b_1 \sum_{i = 1}^{n} x_i} {n} \label{5.5}\]
Хоча Equation\ ref {5.4} і Equation\ ref {5.5} виглядають грізними, необхідно лише оцінити наступні чотири підсумовування
\[\sum_{i = 1}^{n} x_i \quad \sum_{i = 1}^{n} y_i \quad \sum_{i = 1}^{n} x_i y_i \quad \sum_{i = 1}^{n} x_i^2 \nonumber\]
Багато калькуляторів, електронних таблиць та інших статистичних програмних пакетів здатні виконувати лінійний регресійний аналіз на основі цієї моделі. Щоб заощадити час і уникнути виснажливих розрахунків, дізнайтеся, як використовувати один із цих інструментів (докладніше про завершення лінійного регресійного аналізу за допомогою Excel та R. Для наочних цілей необхідні розрахунки детально показані на наступному прикладі.
Рівняння\ ref {5.4} і Equation\ ref {5.5} записуються через загальні змінні x і y. Коли ви працюєте над цим прикладом, пам'ятайте, що x відповідає C std, а що y відповідає S std.
Використовуючи дані з таблиці Template:index, визначте зв'язок між S std і C std за допомогою незваженої лінійної регресії.
Рішення
Ми починаємо з налаштування таблиці, яка допоможе нам організувати розрахунок.
| \(x_i\) | \(y_i\) | \(x_i y_i\) | \(x_i^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (x_i y_i\) ">0.000 | \ (x_i ^ 2\) ">0.000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (x_i\) ">1.236 | \ (x_i^2\) ">0,010 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (x_i\) ">4.966 | \ (x_i^2\) ">0,040 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (x_i\) ">10.773 | \ (x_i^2\) ">0,090 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (x_i\) ">19.516 | \ (x_i^2\) ">0.160 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (x_i\) ">30.210 | \ (x_i^2\) ">0,250 |
Додавання значень у кожному стовпці дає
\[\sum_{i = 1}^{n} x_i = 1.500 \quad \sum_{i = 1}^{n} y_i = 182.31 \quad \sum_{i = 1}^{n} x_i y_i = 66.701 \quad \sum_{i = 1}^{n} x_i^2 = 0.550 \nonumber\]
Підставляючи ці значення в Equation\ ref {5.4} і Equation\ ref {5.5}, ми виявимо, що нахил і y -перехоплення є
\[b_1 = \frac {(6 \times 66.701) - (1.500 \times 182.31)} {(6 \times 0.550) - (1.500)^2} = 120.706 \approx 120.71 \nonumber\]
\[b_0 = \frac {182.31 - (120.706 \times 1.500)} {6} = 0.209 \approx 0.21 \nonumber\]
Відносини між сигналом і аналітом, отже, є
\[S_{std} = 120.71 \times C_{std} + 0.21 \nonumber\]
Наразі ми зберігаємо два знака після коми, щоб відповідати кількості десяткових знаків у сигналі. Отриману калібрувальну криву показано на рисунку Template:index.
Невизначеність у регресійному аналізі
Як показано на малюнку Template:index, оскільки невизначені помилки в сигналі, лінія регресії може не проходити через точний центр кожної точки даних. Сукупне відхилення наших даних від лінії регресії - тобто загальної залишкової помилки - пропорційно невизначеності в регресії. Ми називаємо цю невизначеність стандартним відхиленням про регресію, s r, яка дорівнює
\[s_r = \sqrt{\frac {\sum_{i = 1}^{n} \left( y_i - \hat{y}_i \right)^2} {n - 2}} \label{5.6}\]
де y i - i експериментальне значення, і\(\hat{y}_i\) відповідне значення, передбачене лінією регресії в Equation\ ref {5.2}. Зауважте, що знаменник Equation\ ref {5.6} вказує на те, що наш регресійний аналіз має n - 2 ступені свободи - ми втрачаємо два ступені свободи, оскільки використовуємо для обчислення два параметри: нахил і y -перехоплення\(\hat{y}_i\).
Ви помітили схожість між стандартним відхиленням щодо регресії (Equation\ ref {5.6}) та стандартним відхиленням для вибірки (Equation 4.1.1)?
Більш корисним поданням невизначеності в нашому регресійному аналізі є врахування впливу невизначених помилок на нахил, b 1, і y -перехоплення, b 0, який ми виражаємо як стандартні відхилення.
Ми використовуємо ці стандартні відхилення для встановлення довірчих інтервалів для очікуваного нахилу\(\beta_1\), і очікуваного y -перехоплення,\(\beta_0\)
\[\beta_1 = b_1 \pm t s_{b_1} \label{5.9}\]
\[\beta_0 = b_0 \pm t s_{b_0} \label{5.10}\]
де виділено t для рівня значущості,\(\alpha\) а для n — 2 ступенів свободи. Зауважте, що Equation\ ref {5.9} та Equation\ ref {5.10} не містять множника,\((\sqrt{n})^{-1}\) оскільки довірчий інтервал базується на одній лінії регресії.
Обчисліть 95% довірчих інтервалів для нахилу та y -перехоплення з Прикладу Template:index.
Рішення
Почнемо з розрахунку стандартного відхилення про регресію. Для цього ми повинні обчислити передбачені сигнали\(\hat{y}_i\), використовуючи нахил і y -перехоплення з Прикладу Template:index, і квадрати залишкової помилки,\((y_i - \hat{y}_i)^2\). Використовуючи останній стандарт як приклад, ми виявимо, що передбачуваний сигнал
\[\hat{y}_6 = b_0 + b_1 x_6 = 0.209 + (120.706 \times 0.500) = 60.562 \nonumber\]
і що квадрат залишкової помилки
\[(y_i - \hat{y}_i)^2 = (60.42 - 60.562)^2 = 0.2016 \approx 0.202 \nonumber\]
Наступна таблиця відображає результати для всіх шести рішень.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) |
\(\left( y_i - \hat{y}_i \right)^2\) |
|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (\ hat {y} _i\) ">0.209 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0437 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (\ hat {y} _i\) ">12.280 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0064 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (\ hat {y} _i\) ">24.350 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.2304 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (\ hat {y} _i\) ">36.421 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.2611 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (\ hat {y} _i\) ">48.491 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0894 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (\ hat {y} _i\) ">60.562 | \ (\ ліворуч (y_i -\ hat {y} _i\ праворуч) ^2\) ">0.0202 |
Складання даних в останньому стовпці дає чисельник Equation\ ref {5.6} як 0.6512; таким чином, стандартне відхилення щодо регресії дорівнює
\[s_r = \sqrt{\frac {0.6512} {6 - 2}} = 0.4035 \nonumber\]
Далі обчислюємо стандартні відхилення для ухилу і y -перехоплення за допомогою Equation\ ref {5.7} і Equation\ ref {5.8}. Значення термінів підсумовування взято з Прикладу Template:index.
\[s_{b_1} = \sqrt{\frac {6 \times (0.4035)^2} {(6 \times 0.550) - (1.500)^2}} = 0.965 \nonumber\]
\[s_{b_0} = \sqrt{\frac {(0.4035)^2 \times 0.550} {(6 \times 0.550) - (1.500)^2}} = 0.292 \nonumber\]
Нарешті, 95% довірчих інтервалів (\(\alpha = 0.05\)4 ступеня свободи) для нахилу та y -перехоплення є
\[\beta_1 = b_1 \pm ts_{b_1} = 120.706 \pm (2.78 \times 0.965) = 120.7 \pm 2.7 \nonumber\]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.209 \pm (2.78 \times 0.292) = 0.2 \pm 0.80 \nonumber\]
де t (0,05, 4) з додатка 4 дорівнює 2.78. Стандартне відхилення щодо регресії, s r, говорить про те, що сигнал, S std, є точним до одного знака після коми. З цієї причини ми повідомляємо нахил і y -перехоплення до одного знака після коми.
Мінімізація невизначеності в моделі калібрування
Щоб мінімізувати невизначеність нахилу калібрувальної кривої та y -перехоплення, ми рівномірно розміщуємо наші стандарти в широкому діапазоні концентрацій аналітів. Уважне вивчення Equation\ ref {5.7} і Equation\ ref {5.8} допоможе нам зрозуміти, чому це правда. Знаменники обох рівнянь включають в себе термін\(\sum_{i = 1}^{n} (x_i - \overline{x}_i)^2\). Чим більше значення цього терміна - що ми досягаємо, збільшуючи діапазон x навколо його середнього значення - менше стандартні відхилення в нахилі і y -перехоплення. Крім того, щоб мінімізувати невизначеність у -перехопленні, це допомагає зменшити значення члена\(\sum_{i = 1}^{n} x_i\) в Equation\ ref {5.8}, що ми досягаємо, включивши стандарти для нижчих концентрацій аналіту.
Отримання концентрації аналіту з рівняння регресії
Після того, як ми отримаємо наше рівняння регресії, легко визначити концентрацію аналіту в зразку. Наприклад, коли ми використовуємо нормальну калібрувальну криву, ми вимірюємо сигнал для нашого зразка, S samp, і обчислюємо концентрацію аналіта, C A, використовуючи рівняння регресії.
\[C_A = \frac {S_{samp} - b_0} {b_1} \label{5.11}\]
Менш очевидним є те, як повідомити про довірчий інтервал для C A, який виражає невизначеність в нашому аналізі. Для обчислення довірчого інтервалу нам потрібно знати стандартне відхилення в концентрації аналіта\(s_{C_A}\), яке задається наступним рівнянням
де m - кількість реплікації, яку ми використовуємо для встановлення середнього сигналу зразка, S samp, n - кількість калібрувальних стандартів, S std - середній сигнал для калібрування стандарти,\(C_{std_1}\) і\(\overline{C}_{std}\) є індивідуальними та середніми концентраціями для стандартів калібрування. Знаючи значення\(s_{C_A}\), довірчий інтервал для концентрації аналіта становить
\[\mu_{C_A} = C_A \pm t s_{C_A} \nonumber\]
де\(\mu_{C_A}\) - очікуване значення С А при відсутності детермінантних похибок, а при значенні t базується на бажаному рівні довіри і n — 2 ступеня свободи.
Рівняння\ ref {5.12} записано в терміні калібрувального експерименту. Тут наведено більш загальну форму рівняння, записаного через x і y.
\[s_{x} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{Y} - \overline{y} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber\]
Уважне вивчення Equation\ ref {5.12} має переконати вас, що невизначеність в C A є найменшою\(\overline{S}_{samp}\), коли середній сигнал вибірки, дорівнює середньому сигналу для стандартів,\(\overline{S}_{std}\). Коли це практично, слід спланувати калібрувальну криву так, щоб S samp потрапляла посередині калібрувальної кривої. Для отримання додаткової інформації про ці рівняння регресії див. (а) Міллер, Дж. Аналітик 1991, 116, 3—14; (б) Шараф, М.А.; Іллман, Д.Л.; Ковальський, Б.Р. Chemometrics, Wiley-Interscience: Нью-Йорк, 1986, стор. 126-127; (c) Комітет з аналітичних методів» Невизначеність концентрацій, оцінених в результаті калібрувальних експериментів», Технічний бриф КУА, березень 2006.
Три репліковані аналізи для зразка, який містить невідому концентрацію аналіту, значення виходу для S samp 29,32, 29.16 та 29.51 (довільні одиниці). Використовуючи результати з Прикладу Template:index та Example Template:index, визначте концентрацію аналіта, C A та його 95% довірчий інтервал.
Рішення
Середній сигнал 29.33\(\overline{S}_{samp}\), який, використовуючи Equation\ ref {5.11} і нахил і y -перехоплення з Приклад Template:index, дає концентрацію аналіта як
\[C_A = \frac {\overline{S}_{samp} - b_0} {b_1} = \frac {29.33 - 0.209} {120.706} = 0.241 \nonumber\]
Щоб розрахувати стандартне відхилення для концентрації аналіта, ми повинні визначити значення для\(\overline{S}_{std}\) і за\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\). Перший є лише середнім сигналом для стандартів калібрування, який, використовуючи дані таблиці Template:index, дорівнює 30.385. Обчислення\(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\) виглядає грізним, але ми можемо спростити його обчислення, визнавши, що ця сума квадратів є чисельником у рівнянні стандартного відхилення; таким чином,
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (s_{C_{std}})^2 \times (n - 1) \nonumber\]
де\(s_{C_{std}}\) - стандартне відхилення для концентрації аналіту в нормах калібрування. Використовуючи дані в таблиці Template:index, ми виявимо, що\(s_{C_{std}}\) це 0.1871 і
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (0.1872)^2 \times (6 - 1) = 0.175 \nonumber\]
Підстановка відомих значень у рівняння\ ref {5.12} дає
\[s_{C_A} = \frac {0.4035} {120.706} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(29.33 - 30.385)^2} {(120.706)^2 \times 0.175}} = 0.0024 \nonumber\]
Нарешті, 95% довірчий інтервал для 4 ступенів свободи
\[\mu_{C_A} = C_A \pm ts_{C_A} = 0.241 \pm (2.78 \times 0.0024) = 0.241 \pm 0.007 \nonumber\]
На малюнку Template:index показано калібрувальну криву з кривими, що показують 95% довірчий інтервал для C A.
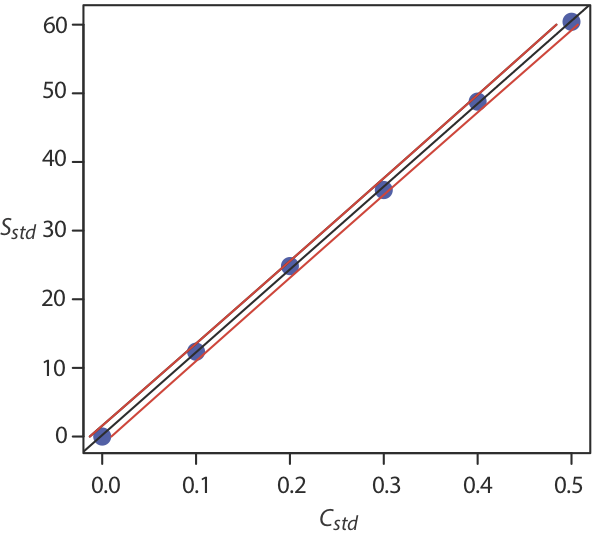
У стандартному доповненні ми визначаємо концентрацію аналіта шляхом екстраполяції калібрувальної кривої на x -перехоплення. У цьому випадку значення C A дорівнює
\[C_A = x\text{-intercept} = \frac {-b_0} {b_1} \nonumber\]
а стандартне відхилення в С А дорівнює
\[s_{C_A} = \frac {s_r} {b_1} \sqrt{\frac {1} {n} + \frac {(\overline{S}_{std})^2} {(b_1)^2 \sum_{i = 1}^{n}(C_{std_i} - \overline{C}_{std})^2}} \nonumber\]
де n - кількість стандартних доповнень (включаючи зразок без доданого стандарту), і\(\overline{S}_{std}\) є середнім сигналом для n стандартів. Оскільки ми визначаємо концентрацію аналіта шляхом екстраполяції, а не інтерполяцією,\(s_{C_A}\) для методу стандартних доповнень зазвичай більше, ніж для нормальної калібрувальної кривої.
Рисунок Template:index показує нормальну калібрувальну криву для кількісного аналізу Cu 2 +. Дані для калібрувальної кривої наведені тут.
| [Cu 2+] (М) | Поглинання |
|---|---|
| 0 | 0 |
| \(1.55 \times 10^{-3}\) | 0,050 |
| \(3.16 \times 10^{-3}\) | 0.093 |
| \(4.74 \times 10^{-3}\) | 0.143 |
| \(6.34 \times 10^{-3}\) | 0.188 |
| \(7.92 \times 10^{-3}\) | 0,236 |
Виконайте лінійний регресійний аналіз для цих даних калібрування, повідомляючи про рівняння калібрування та 95% довірчий інтервал для нахилу та y -перехоплення. Якщо три репліковані зразки дають S samp 0,114, яка концентрація аналіту в зразку та його 95% довірчий інтервал?
- Відповідь
-
Починаємо з налаштування таблиці, яка допоможе нам організувати розрахунок
\(x_i\) \(y_i\) \(x_i y_i\) \(x_i^2\) \ (x_i\) ">0.000 \ (y_i\) ">0.000 \ (x_i y_i\) ">0.000 \ (x_i ^ 2\) ">0.000 \ (x_i\) ">\(1.55 \times 10^{-3}\) \ (y_i\) ">0,050 \ (x_i y_i\) ">\(7.750 \times 10^{-5}\) \ (x_i^2\) ">\(2.403 \times 10^{-6}\) \ (x_i\) ">\(3.16 \times 10^{-3}\) \ (y_i\) ">0,093 \ (x_i y_i\) ">\(2.939 \times 10^{-4}\) \ (x_i^2\) ">\(9.986 \times 10^{-6}\) \ (x_i\) ">\(4.74 \times 10^{-3}\) \ (y_i\) ">0.143 \ (x_i y_i\) ">\(6.778 \times 10^{-4}\) \ (x_i^2\) ">\(2.247 \times 10^{-5}\) \ (x_i\) ">\(6.34 \times 10^{-3}\) \ (y_i\) ">0.188 \ (x_i y_i\) ">\(1.192 \times 10^{-3}\) \ (x_i^2\) ">\(4.020 \times 10^{-5}\) \ (x_i\) ">\(7.92 \times 10^{-3}\) \ (y_i\) ">0,236 \ (x_i y_i\) ">\(1.869 \times 10^{-3}\) \ (x_i^2\) ">\(6.273 \times 10^{-5}\) Додавання значень у кожному стовпці дає
\[\sum_{i = 1}^{n} x_i = 2.371 \times 10^{-2} \quad \sum_{i = 1}^{n} y_i = 0.710 \quad \sum_{i = 1}^{n} x_i y_i = 4.110 \times 10^{-3} \quad \sum_{i = 1}^{n} x_i^2 = 1.378 \times 10^{-4} \nonumber\]
Коли ми підставляємо ці значення в Equation\ ref {5.4} і Equation\ ref {5.5}, ми виявимо, що нахил і y -перехоплення
\[b_1 = \frac {6 \times (4.110 \times 10^{-3}) - (2.371 \times 10^{-2}) \times 0.710} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}) = 29.57 \nonumber\]
\[b_0 = \frac {0.710 - 29.57 \times (2.371 \times 10^{-2}} {6} = 0.0015 \nonumber\]
і що рівняння регресії
\[S_{std} = 29.57 \times C_{std} + 0.0015 \nonumber\]
Щоб розрахувати 95% довірчих інтервалів, спочатку потрібно визначити стандартне відхилення щодо регресії. Наведена нижче таблиця допомагає нам організувати розрахунок.
\(x_i\) \(y_i\) \(\hat{y}_i\) \((y_i - \hat{y}_i)^2\) \ (x_i\) ">0.000 \ (y_i\) ">0.000 \ (\ hat {y} _i\) ">0.0015 \ ((y_i -\ hat {y} _i) ^2\) ">\(2.250 \times 10^{-6}\) \ (x_i\) ">\(1.55 \times 10^{-3}\) \ (y_i\) ">0,050 \ (\ hat {y} _i\) ">0.0473 \ ((y_i -\ hat {y} _i) ^2\) ">\(7.110 \times 10^{-6}\) \ (x_i\) ">\(3.16 \times 10^{-3}\) \ (y_i\) ">0,093 \ (\ hat {y} _i\) ">0.0949 \ ((y_i -\ hat {y} _i) ^2\) ">\(3.768 \times 10^{-6}\) \ (x_i\) ">\(4.74 \times 10^{-3}\) \ (y_i\) ">0.143 \ (\ hat {y} _i\) ">0.1417 \ ((y_i -\ hat {y} _i) ^2\) ">\(1.791 \times 10^{-6}\) \ (x_i\) ">\(6.34 \times 10^{-3}\) \ (y_i\) ">0.188 \ (\ hat {y} _i\) ">0.1890 \ ((y_i -\ hat {y} _i) ^2\) ">\(9.483 \times 10^{-6}\) \ (x_i\) ">\(7.92 \times 10^{-3}\) \ (y_i\) ">0,236 \ (\ hat {y} _i\) ">0.2357 \ ((y_i -\ hat {y} _i) ^2\) ">\(9.339 \times 10^{-6}\) Складання даних в останньому стовпці дає чисельник Equation\ ref {5.6} as\(1.596 \times 10^{-5}\). Стандартне відхилення щодо регресії, отже,
\[s_r = \sqrt{\frac {1.596 \times 10^{-5}} {6 - 2}} = 1.997 \times 10^{-3} \nonumber\]
Далі нам потрібно обчислити стандартні відхилення для ухилу і y -перехоплення за допомогою Equation\ ref {5.7} і Equation\ ref {5.8}.
\[s_{b_1} = \sqrt{\frac {6 \times (1.997 \times 10^{-3})^2} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}} = 0.3007 \nonumber\]
\[s_{b_0} = \sqrt{\frac {(1.997 \times 10^{-3})^2 \times (1.378 \times 10^{-4})} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}} = 1.441 \times 10^{-3} \nonumber\]
і використовувати їх для обчислення 95% довірчих інтервалів для нахилу і y -перехоплення
\[\beta_1 = b_1 \pm ts_{b_1} = 29.57 \pm (2.78 \times 0.3007) = 29.57 \text{ M}^{-1} \pm 0.84 \text{ M}^{-1} \nonumber\]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.0015 \pm (2.78 \times 1.441 \times 10^{-3}) = 0.0015 \pm 0.0040 \nonumber\]
При середній самці S 0,114 концентрація аналіту, С А, становить
\[C_A = \frac {S_{samp} - b_0} {b_1} = \frac {0.114 - 0.0015} {29.57 \text{ M}^{-1}} = 3.80 \times 10^{-3} \text{ M} \nonumber\]
Стандартне відхилення в С А дорівнює
\[s_{C_A} = \frac {1.997 \times 10^{-3}} {29.57} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(0.114 - 0.1183)^2} {(29.57)^2 \times (4.408 \times 10^{-5})}} = 4.778 \times 10^{-5} \nonumber\]
і 95% довіри інтервал
\[\mu = C_A \pm t s_{C_A} = 3.80 \times 10^{-3} \pm \{2.78 \times (4.778 \times 10^{-5})\} \nonumber\]
\[\mu = 3.80 \times 10^{-3} \text{ M} \pm 0.13 \times 10^{-3} \text{ M} \nonumber\]
Оцінка моделі лінійної регресії
Ніколи не слід приймати результат лінійного регресійного аналізу без оцінки достовірності моделі. Мабуть, найпростішим способом оцінки регресійного аналізу є вивчення залишкових помилок. Як ми бачили раніше, залишкова похибка для єдиного стандарту калібрування, r i, дорівнює
\[r_i = (y_i - \hat{y}_i) \nonumber\]
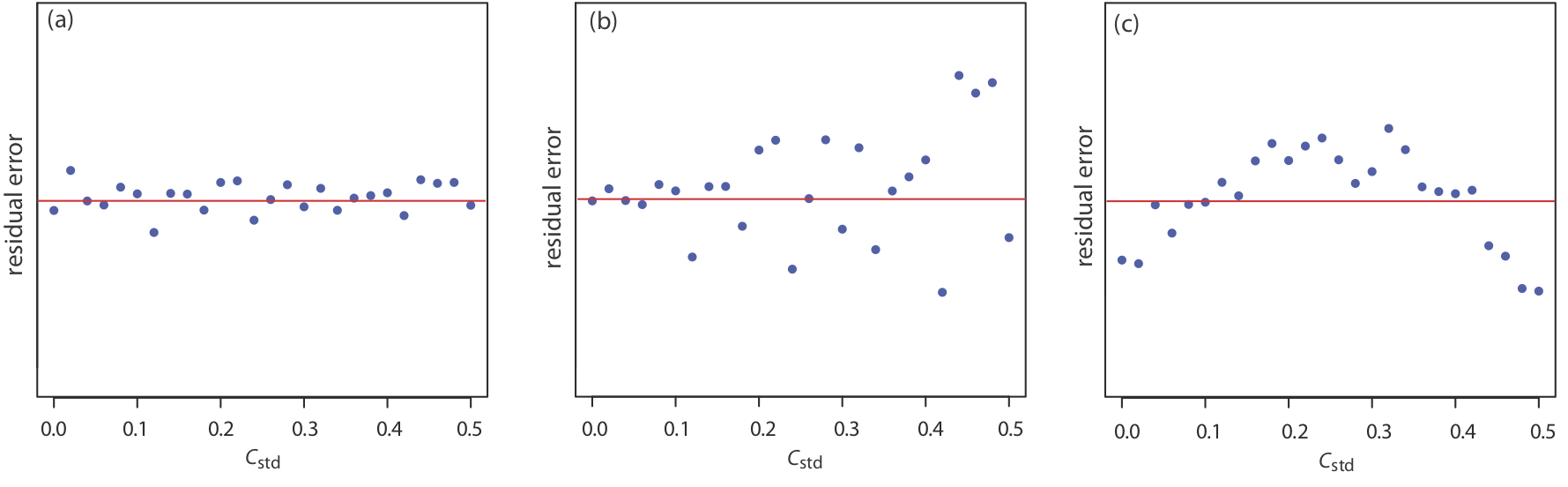
Якщо модель регресії дійсна, залишкові помилки слід розподіляти випадковим чином щодо середньої залишкової помилки нуля, без видимої тенденції до менших або більших залишкових помилок (Рисунок Template:index a). Такі тенденції, як наведені на рисунку Template:index b та Figure Template:index c, свідчать про те, що принаймні одне з припущень моделі є неправильним. Наприклад, тенденція до більших залишкових помилок при більш високих концентраціях, рис. Template:index b, свідчить про те, що невизначені помилки, що впливають на сигнал, не залежать від концентрації аналіта. На рисунку Template:index c залишкові помилки не є випадковими, що говорить про те, що ми не можемо моделювати дані за допомогою прямолінійного зв'язку. Регресійні методи для останніх двох випадків розглядаються в наступних розділах.
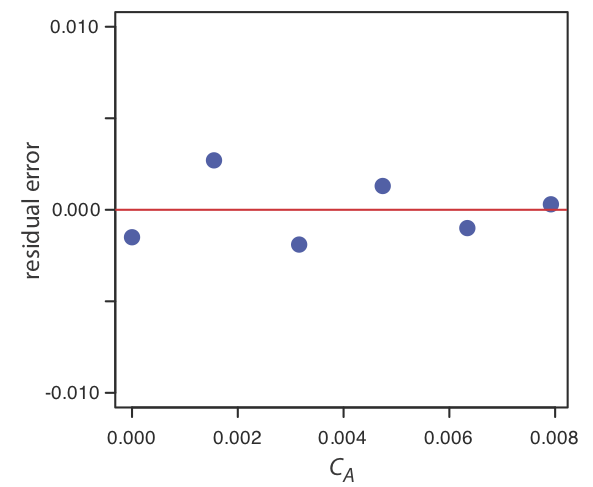
Використовуючи ваші результати з вправи Template:index, побудуйте залишковий графік і поясніть його значення.
- Відповідь
-
Для створення залишкової ділянки нам потрібно обчислити залишкову похибку для кожного стандарту. Наступна таблиця містить відповідну інформацію.
\(x_i\) \(y_i\) \(\hat{y}_i\) \(y_i - \hat{y}_i\) \ (x_i\) ">0.000 \ (y_i\) ">0.000 \ (\ hat {y} _i\) ">0.0015 \ (y_i -\ hat {y} _i\) ">—0.0015 \ (x_i\) ">\(1.55 \times 10^{-3}\) \ (y_i\) ">0,050 \ (\ hat {y} _i\) ">0.0473 \ (y_i -\ hat {y} _i\) ">0.0027 \ (x_i\) ">\(3.16 \times 10^{-3}\) \ (y_i\) ">0,093 \ (\ hat {y} _i\) ">0.0949 \ (y_i -\ hat {y} _i\) ">—0.0019 \ (x_i\) ">\(4.74 \times 10^{-3}\) \ (y_i\) ">0.143 \ (\ hat {y} _i\) ">0.1417 \ (y_i -\ hat {y} _i\) ">0.0013 \ (x_i\) ">\(6.34 \times 10^{-3}\) \ (y_i\) ">0.188 \ (\ hat {y} _i\) ">0.1890 \ (y_i -\ hat {y} _i\) ">—0,0010 \ (x_i\) ">\(7.92 \times 10^{-3}\) \ (y_i\) ">0,236 \ (\ hat {y} _i\) ">0.2357 \ (y_i -\ hat {y} _i\) ">0.0003 На малюнку нижче показана схема отриманих залишкових помилок. Залишкові помилки з'являються випадковими, хоча вони чергуються за знаком, і які не показують значної залежності від концентрації аналіта. Узяті разом ці спостереження свідчать про те, що наша регресійна модель є доречною.
Зважена лінійна регресія з помилками у y
Наша обробка лінійної регресії до цього моменту передбачає, що невизначені помилки, що впливають на y, не залежать від значення x. Якщо це припущення є помилковим, як це стосується даних на малюнку Template:index b, то ми повинні включити дисперсію для кожного значення y до нашого визначення y -перехоплення, b 0 та нахилу, b 1; таким чином
\[b_0 = \frac {\sum_{i = 1}^{n} w_i y_i - b_1 \sum_{i = 1}^{n} w_i x_i} {n} \label{5.13}\]
де w i - ваговий коефіцієнт, який враховує дисперсію в y i
\[w_i = \frac {n (s_{y_i})^{-2}} {\sum_{i = 1}^{n} (s_{y_i})^{-2}} \label{5.15}\]
і\(s_{y_i}\) є стандартним відхиленням для y i. У зваженій лінійній регресії внесок кожної xy -пари в лінію регресії обернено пропорційний точності y i; тобто чим точніше значення y, тим більший її внесок у регресія.
Тут наведені дані для зовнішньої стандартизації, в якій s std є стандартним відхиленням для трьох реплікаційних визначення сигналу. Це ті самі дані, які використовуються в прикладі Template:index з додатковою інформацією про стандартні відхилення сигналу.
| \(C_{std}\)(довільні одиниці) | \(S_{std}\)(довільні одиниці) | \(s_{std}\) |
|---|---|---|
| \ (C_ {std}\) (довільні одиниці виміру) ">0.000 | \ (S_ {std}\) (довільні одиниці виміру) ">0.00 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.100 | \ (S_ {std}\) (довільні одиниці виміру) ">12.36 | \ (s_ {std}\) ">0.02 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.200 | \ (S_ {std}\) (довільні одиниці виміру) ">24.83 | \ (s_ {std}\) ">0.07 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.300 | \ (S_ {std}\) (довільні одиниці виміру) ">35.91 | \ (s_ {std}\) ">0.13 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.400 | \ (S_ {std}\) (довільні одиниці виміру) ">48.79 | \ (s_ {std}\) ">0.22 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.500 | \ (S_ {std}\) (довільні одиниці виміру) ">60.42 | \ (s_ {std}\) ">0.33 |
Визначте рівняння калібрувальної кривої за допомогою зваженої лінійної регресії. Коли ви працюєте над цим прикладом, пам'ятайте, що x відповідає C std, а що y відповідає S std.
Рішення
Ми починаємо з налаштування таблиці, яка допоможе в обчисленні вагових коефіцієнтів.
| \(C_{std}\)(довільні одиниці) | \(S_{std}\)(довільні одиниці) | \(s_{std}\) | \((s_{y_i})^{-2}\) | \(w_i\) |
|---|---|---|---|---|
| \ (C_ {std}\) (довільні одиниці виміру) ">0.000 | \ (S_ {std}\) (довільні одиниці виміру) ">0.00 | \ (s_ {std}\) ">0.02 | \ (s_ {y_i}) ^ {-2}\) ">2500.00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.100 | \ (S_ {std}\) (довільні одиниці виміру) ">12.36 | \ (s_ {std}\) ">0.02 | \ (s_ {y_i}) ^ {-2}\) ">250.00 | \ (w_i\) ">2.8339 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.200 | \ (S_ {std}\) (довільні одиниці виміру) ">24.83 | \ (s_ {std}\) ">0.07 | \ (s_ {y_i}) ^ {-2}\) ">204.08 | \ (w_i\) ">0.2313 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.300 | \ (S_ {std}\) (довільні одиниці виміру) ">35.91 | \ (s_ {std}\) ">0.13 | \ (s_ {y_i}) ^ {-2}\) ">59,17 | \ (w_i\) ">0.0671 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.400 | \ (S_ {std}\) (довільні одиниці виміру) ">48.79 | \ (s_ {std}\) ">0.22 | \ (s_ {y_i}) ^ {-2}\) ">20.66 | \ (w_i\) ">0.0234 |
| \ (C_ {std}\) (довільні одиниці виміру) ">0.500 | \ (S_ {std}\) (довільні одиниці виміру) ">60.42 | \ (s_ {std}\) ">0.33 | \ (s_ {y_i}) ^ {-2}\) ">9.18 | \ (w_i\) ">0.0104 |
Складання значень у четвертому стовпці дає
\[\sum_{i = 1}^{n} (s_{y_i})^{-2} \nonumber\]
які ми використовуємо для обчислення індивідуальних ваг в останньому стовпці. Як перевірки на ваших розрахунках сума окремих ваг повинна дорівнювати числу калібрувальних нормативів, n. Сума записів в останньому стовпці дорівнює 6.0000, тому все добре. Після обчислення окремих ваг ми використовуємо другу таблицю для обчислення чотирьох термінів підсумовування в Equation\ ref {5.13} і Equation\ ref {5.14}.
| \(x_i\) | \(y_i\) | \(w_i\) | \(w_i x_i\) | \(w_i y_i\) | \(w_i x_i^2\) | \(w_i x_i y_i\) |
|---|---|---|---|---|---|---|
| \ (x_i\) ">0.000 | \ (y_i\) ">0.00 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0,0000 | \ (w_i y_i\) ">0,0000 | \ (w_i x_i^2\) ">0,0000 | \ (w_i x_i y_i\) ">0,0000 |
| \ (x_i\) ">0.100 | \ (y_i\) ">12,36 | \ (w_i\) ">2.8339 | \ (w_i x_i\) ">0.2834 | \ (w_i\) ">35.0270 | \ (w_i x_i^2\) ">0.0283 | \ (w_i x_i\) ">3.5027 |
| \ (x_i\) ">0,200 | \ (y_i\) ">24.83 | \ (w_i\) ">0.2313 | \ (w_i x_i\) ">0.0463 | \ (w_i\) ">5.7432 | \ (w_i x_i^2\) ">0,0093 | \ (w_i x_i\) ">1.1486 |
| \ (x_i\) ">0,300 | \ (y_i\) ">35.91 | \ (w_i\) ">0.0671 | \ (w_i x_i\) ">0.0201 | \ (w_i\) ">2.4096 | \ (w_i x_i^2\) ">0,0060 | \ (w_i x_i\) ">0.7229 |
| \ (x_i\) ">0,400 | \ (y_i\) ">48.79 | \ (w_i\) ">0.0234 | \ (w_i x_i\) ">0,0094 | \ (w_i\) ">1.1417 | \ (w_i x_i^2\) ">0.0037 | \ (w_i x_i\) ">0,4567 |
| \ (x_i\) ">0,500 | \ (y_i\) ">60.42 | \ (w_i\) ">0.0104 | \ (w_i x_i\) ">0,0052 | \ (w_i\) ">0.6284 | \ (w_i x_i^2\) ">0,0026 | \ (w_i x_i\) ">0.3142 |
Додавання значень в останніх чотирьох стовпцях дає
\[\sum_{i = 1}^{n} w_i x_i = 0.3644 \quad \sum_{i = 1}^{n} w_i y_i = 44.9499 \quad \sum_{i = 1}^{n} w_i x_i^2 = 0.0499 \quad \sum_{i = 1}^{n} w_i x_i y_i = 6.1451 \nonumber\]
Підставляючи ці значення в Рівняння\ ref {5.13} і Equation\ ref {5.14} дає розрахунковий нахил і оцінений y -перехоплення як
\[b_1 = \frac {(6 \times 6.1451) - (0.3644 \times 44.9499)} {(6 \times 0.0499) - (0.3644)^2} = 122.985 \nonumber\]
\[b_0 = \frac{44.9499 - (122.985 \times 0.3644)} {6} = 0.0224 \nonumber\]
Рівняння калібрування
\[S_{std} = 122.98 \times C_{std} + 0.2 \nonumber\]
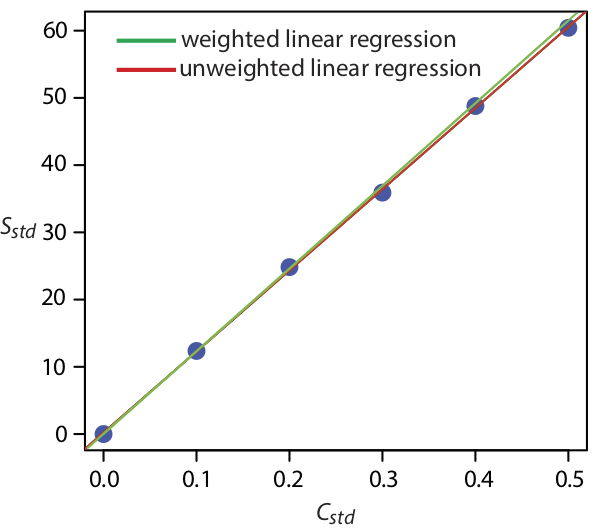
Рисунок Template:index показує калібрувальну криву для зваженої регресії та калібрувальну криву для незваженої регресії у прикладі Template:index. Хоча дві калібрувальні криві дуже схожі, є невеликі відмінності в нахилі та у -перехопленні. Найбільш примітно, що y -перехоплення для зваженої лінійної регресії ближче до очікуваного значення нуля. Оскільки стандартне відхилення для сигналу, S std, менше для менших концентрацій аналіту, C STD, зважена лінійна регресія надає більше уваги цим стандартам, що дозволяє краще оцінити y -перехоплення.
Рівняння для обчислення довірчих інтервалів для нахилу, y -перехоплення та концентрації аналіту при використанні зваженої лінійної регресії визначити не так просто, як для незваженої лінійної регресії [Bonate, P.J. Anal. Хім. 1993, 65, 1367—1372]. Однак довірчий інтервал для концентрації аналіта знаходиться на оптимальному значенні, коли сигнал аналіта знаходиться поблизу зважених центроїдів, y c, калібрувальної кривої.
\[y_c = \frac {1} {n} \sum_{i = 1}^{n} w_i x_i \nonumber\]
Зважена лінійна регресія з помилками як у x, так і у
Якщо ми приберемо наше припущення, що невизначені помилки, що впливають на калібрувальну криву, присутні тільки в сигналі (y), то ми також повинні враховувати в регресійній моделі невизначені помилки, які впливають на концентрацію аналіта в стандартах калібрування (x). Рішення для результуючої лінії регресії більш задіяно, ніж для незважених або зважених ліній регресії. Хоча ми не будемо розглядати деталі в цьому підручнику, ви повинні знати, що нехтування наявністю невизначеної помилки в x може змістити результати лінійної регресії.
Див., наприклад, Комітет з аналітичних методів, «Встановлення лінійного функціонального зв'язку до даних з помилкою обох змінних», Технічний бриф КУА, березень 2002), а також додаткові ресурси цієї глави.
Криволінійна і багатовимірна регресія
Прямолінійна регресійна модель, незважаючи на її очевидну складність, є найпростішим функціональним зв'язком між двома змінними. Що ми робимо, якщо наша калібрувальна крива криволінійна - тобто, якщо це крива, а не пряма? Один з підходів полягає в тому, щоб спробувати перетворити дані в пряму лінію. Таким чином були використані логарифми, експоненціальні, зворотні, квадратні корені та тригонометричні функції. Типовим прикладом є графік log (y) проти x. Такі перетворення не позбавлені ускладнень, з яких найбільш очевидним є те, що дані з рівномірною дисперсією в y не збережуть цю рівномірну дисперсію після її перетворення.
Варто відзначити, що термін «лінійний» не означає пряму. Лінійна функція може містити більше одного адитивного члена, але кожен такий термін має один і тільки один регульований мультиплікативний параметр. Функція
\[y = ax + bx^2 \nonumber\]
є прикладом лінійної функції, оскільки терміни x та x 2 містять один мультиплікативний параметр, a та b відповідно. Функція
\[y = x^b \nonumber\]
є нелінійним, оскільки b не є мультиплікативним параметром; це, натомість, потужність. Ось чому ви можете використовувати лінійну регресію, щоб пристосувати поліноміальне рівняння до ваших даних.
Іноді вдається перетворити нелінійну функцію в лінійну функцію. Наприклад, взяття журналу обох сторін нелінійної функції вище дає лінійну функцію.
\[\log(y) = b \log(x) \nonumber\]
Іншим підходом до розробки моделі лінійної регресії є пристосування поліноміального рівняння до даних, таких як\(y = a + b x + c x^2\). Ви можете використовувати лінійну регресію для обчислення параметрів a, b та c, хоча рівняння відрізняються від рівнянь для лінійної регресії прямої. Якщо ви не можете вмістити дані за допомогою одного поліноміального рівняння, можливо, можна встановити окремі поліноміальні рівняння до коротких відрізків калібрувальної кривої. Результатом є одна безперервна калібрувальна крива, відома як сплайн-функція.
Детальніше про криволінійну регресію див. (а) Шараф, М.А.; Іллман, Д.Л.; Ковальський, Б.Р. хемометрика, Wiley-Interscience: Нью-Йорк, 1986; (б) Демінг, С.Н.; Морган, С.Л. Експериментальний дизайн: Хемометричний підхід, Elsevier: Амстердам, 1987.
Регресійні моделі в цьому розділі застосовуються лише до функцій, які містять одну незалежну змінну, наприклад сигнал, який залежить від концентрації аналіта. При наявності інтерферента, однак, сигнал може залежати від концентрацій як аналіту, так і інтерферентного
\[S = k_A C_A + k_I CI + S_{reag} \nonumber\]
де k I - чутливість інтерферента, а C I - концентрація інтерферента. Багатовимірні калібрувальні криві готуються з використанням стандартів, які містять відомі кількості як аналіту, так і інтерференту, і моделюються з використанням багатовимірної регресії.
Див. Бібі, К. Р.; Ковальський, Б.Р. анал. Хім. 1987, 59, 1007A—1017A. для отримання додаткової інформації та ознайомтеся з Додатковими ресурсами цього розділу для отримання додаткової інформації про лінійну регресію з помилками обох змінних, криволінійну регресію та багатовимірну регресію.