5.3: Визначення чутливості
- Page ID
- 24960
Для стандартизації аналітичного методу ми також повинні визначити чутливість аналіта, k A, в Equation Template:index або Equation Template:index.
\[S_{total} = k_A n_A + S_{reag} \label{5.1}\]
\[S_{total} = k_A C_A + S_{reag} \label{5.2}\]
В принципі, можна вивести значення k A для будь-якого аналітичного методу, якщо зрозуміти повністю всі хімічні реакції і фізичні процеси, що відповідають за сигнал. На жаль, такі розрахунки нездійсненні, якщо бракує достатньо розвиненої теоретичної моделі фізичних процесів або якщо хімічна реакція свідчить про неідеальну поведінку. У таких ситуаціях ми повинні визначити значення k A шляхом аналізу одного або декількох стандартних рішень, кожен з яких містить відому кількість аналіту. У цьому розділі розглянуто кілька підходів до визначення значення k A. Для простоти ми припустимо, що S reag враховується належним порожнім реагентом, що дозволяє замінити S total в Equation\ ref {5.1} і Equation\ ref {5.2} сигналом аналіта, S А.
Рівняння\ ref {5.3} і Equation\ ref {5.4} по суті ідентичні, відрізняються лише тим, чи ми вибрали вираження кількості аналіту в молі або у вигляді концентрації. Для решти цієї глави ми обмежимо наше лікування рівнянням\ ref {5.4}. Ви можете розширити цю обробку до Equation\ ref {5.3}, замінивши C A на n A.
Одноточкові та множинні стандартизації
Найпростішим способом визначення значення k A в Equation\ ref {5.4} є використання одноточкової стандартизації, в якій ми вимірюємо сигнал для стандарту S std, який містить відому концентрацію аналіту, C стд. Підставляємо ці значення в рівняння\ ref {5.4}
\[k_A = \frac {S_{std}} {C_{std}} \label{5.5}\]
дає нам значення для k A. Визначивши k A, ми можемо обчислити концентрацію аналіту в зразку шляхом вимірювання його сигналу, S samp, і обчислення C A за допомогою Equation\ ref {5.6}.
\[C_A = \frac {S_{samp}} {k_A} \label{5.6}\]
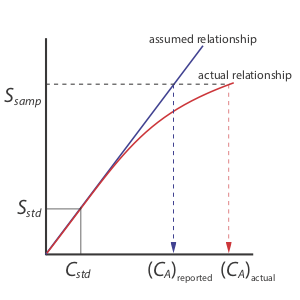
Одноточкова стандартизація є найменш бажаним методом стандартизації методу. Цьому є дві причини. По-перше, будь-яка похибка в нашому визначенні k A переноситься в наш розрахунок C A. По-друге, наше експериментальне значення для k A базується на одній концентрації аналіту. Щоб розширити це значення k A до інших концентрацій аналіту, потрібно припустити лінійну залежність між сигналом і концентрацією аналіта, припущення, яке часто не відповідає дійсності [Кардон, М.Дж.; Palmero, P J.; Sybrandt, LB Anal. Хім. 1980, 52, 1187—1191]. Рисунок Template:index показує, як припущення постійної величини k A призводить до визначеної помилки в C A, якщо k A стає меншим при більш високих концентраціях аналіту. Незважаючи на ці обмеження, одноточкові стандартизації знаходять звичайне використання, коли очікуваний діапазон концентрацій аналіта невеликий. У цих умовах часто можна з упевненістю припустити, що k A є постійним (хоча ви повинні перевірити це припущення експериментально). Так відбувається, наприклад, в клінічних лабораторіях, де багато автоматизованих аналізаторів використовують лише єдиний стандарт.
Кращим способом стандартизації методу є підготовка ряду стандартів, кожен з яких містить різну концентрацію аналіту. Стандарти вибираються такі, що вони відповідають очікуваному діапазону концентрації аналіта. Багатоточкова стандартизація повинна включати щонайменше три стандарти, хоча більш кращими є. Графік S std проти C std називається калібрувальною кривою. Точна стандартизація, або залежність калібрування, визначається відповідним алгоритмом підгонки кривої.
Лінійна регресія, яка також відома як метод найменших квадратів, є одним з таких алгоритмів. Його використання розглянуто в розділі 5.4.
Є дві переваги багатоточкової стандартизації. По-перше, хоча детермінантна помилка в одному стандарті вносить детермінантну похибку, її вплив зводиться до мінімуму іншими стандартами. По-друге, оскільки ми вимірюємо сигнал для декількох концентрацій аналіту, ми більше не повинні вважати, що k A не залежить від концентрації аналіта. Натомість ми можемо побудувати калібрувальну криву, подібну до «фактичного відношення» на малюнку Template:index.
Зовнішні стандарти
Найбільш поширений метод стандартизації використовує один або кілька зовнішніх стандартів, кожен з яких містить відому концентрацію аналіту. Ми називаємо ці стандарти «зовнішніми», оскільки вони готуються і аналізуються окремо від зразків.
Додавання прикметника «зовнішній» до іменника «стандарт» може здатися вам дивним у цей момент, оскільки здається розумним припустити, що стандарти та зразки аналізуються окремо. Однак, як ми скоро дізнаємося, ми можемо додати стандарти до наших зразків і аналізувати обидва одночасно.
Одномісний зовнішній стандарт
За допомогою єдиного зовнішнього стандарту визначаємо k A за допомогою eEquation\ ref {5.5}, а потім обчислюємо концентрацію аналіту C A, використовуючи Equation\ ref {5.6}.
Спектрофотометричний метод кількісного аналізу Pb 2+ в крові дає S std 0,474 для єдиного стандарту, для якого концентрація свинцю становить 1,75 ppb. Яка концентрація Pb 2 + в зразку крові, для якої S самп дорівнює 0,361?
Рішення
Рівняння\ ref {5.5} дозволяє обчислити значення k A, використовуючи дані для єдиного зовнішнього стандарту.
\[k_A = \frac {S_{std}} {C_{std}} = \frac {0.474} {1.75 \text{ ppb}} = 0.2709 \text{ ppb}^{-1} \nonumber\]
Визначивши значення k А, обчислюємо концентрацію Pb 2 + в пробі крові, розраховується за допомогою Equation\ ref {5.6}.
\[C_A = \frac {S_{samp}} {k_A} = \frac {0.361} {0.2709 \text{ ppb}^{-1}} = 1.33 \text{ ppb} \nonumber\]
Кілька зовнішніх стандартів
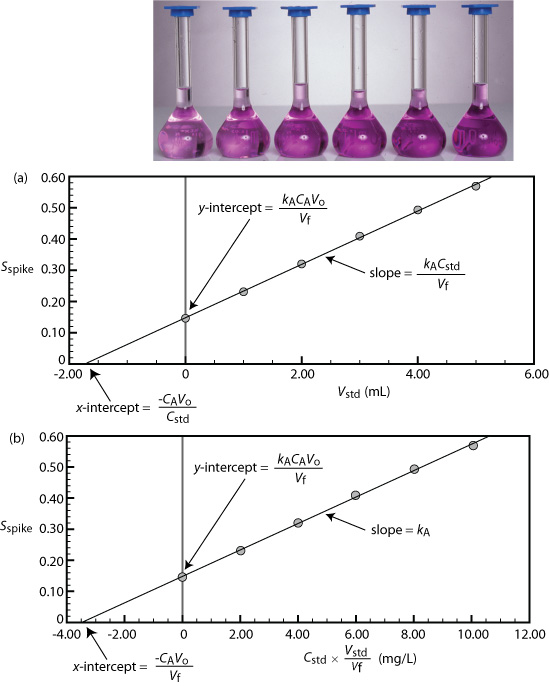
Рисунок Template:index показує типову багатоточкову зовнішню стандартизацію. Об'ємна колба зліва містить заготовку реагенту, а решта об'ємних колб містять зростаючі концентрації Cu 2 +. Нижче наведені об'ємні колби - отримана калібрувальна крива. Оскільки це найпоширеніший метод стандартизації, отримане співвідношення називається нормальною калібрувальною кривою.

Коли калібрувальна крива є прямолінійною, як це показано на рисунку Template:index, нахил прямої дає значення k A. Це найбільш бажана ситуація, оскільки чутливість методу залишається постійною у всьому діапазоні концентрацій аналіта. Коли калібрувальна крива не є прямою, чутливість методу є функцією концентрації аналіта. Наприклад, на малюнку Template:index}, наприклад, значення k A є найбільшим, коли концентрація аналіту мала, і вона постійно зменшується для більш високих концентрацій аналіту. Значення k A в будь-якій точці вздовж калібрувальної кривої на рисунку Template:index є нахилом у цій точці. У будь-якому випадку калібрувальна крива дозволяє пов'язати S samp з концентрацією аналіта.
Другий спектрофотометричний метод кількісного аналізу Pb 2+ в крові має нормальну калібрувальну криву, для якої
\[S_{std} = (0.296 \text{ ppb}^{-1} \times C_{std}) + 0.003 \nonumber\]
Яка концентрація Pb 2 + в зразку крові, якщо S самп дорівнює 0,397?
Рішення
Для визначення концентрації Pb 2 + в зразку крові замінюємо S std в калібрувальному рівнянні на S samp і вирішуємо для C A .
\[C_A = \frac {S_{samp} - 0.003} {0.296 \text{ ppb}^{-1}} = \frac {0.397 - 0.003} {0.296 \text{ ppb}^{-1}} = 1.33 \text{ ppb} \nonumber\]
Варто зазначити, що рівняння калібрування в цій задачі включає додатковий член, який не відображається в Equation\ ref {5.6}. В ідеалі ми очікуємо, що наша калібрувальна крива матиме сигнал нуля, коли C A дорівнює нулю. Це мета використання заготовки реагенту для корекції вимірюваного сигналу. Додатковий член +0,003 в нашому калібрувальному рівнянні є результатом невизначеності вимірювання сигналу для заготовки реагенту та стандартів.
Рисунок Template:index показує нормальну калібрувальну криву для кількісного аналізу Cu 2 +. Рівняння для калібрувальної кривої дорівнює
\[S_{std} = 29.59 \text{ M}^{-1} \times C_{std} + 0.015 \nonumber\]
Яка концентрація Cu 2 + у зразку, поглинання якого, S samp, становить 0,114? Порівняйте свою відповідь з одноточковою стандартизацією, де стандарт\(3.16 \times 10^{-3} \text{ M}\) Cu 2 + дає сигнал 0.0931.
- Відповідь
-
Підставляючи поглинання зразка в калібрувальне рівняння та розв'язування для C A дають
\[S_{samp} = 0.114 = 29.59 \text{ M}^{-1} \times C_{A} + 0.015 \nonumber\]
\[C_A = 3.35 \times 10^{-3} \text{ M} \nonumber\]
Для одноточкової стандартизації спочатку вирішуємо для k A
\[k_A = \frac {S_{std}} {C_{std}} = \frac {0.0931} {3.16 \times 10^{-3} \text{ M}} = 29.46 \text{ M}^{-1} \nonumber\]
а потім використовувати це значення k A для вирішення для C A.
\[C_A = \frac {S_{samp}} {k_A} = \frac {0.114} {29.46 \text{ M}^{-1}} = 3.87 \times 10^{-3} \text{ M} \nonumber\]
При використанні декількох стандартів невизначені помилки, що впливають на сигнал для одного стандарту, частково компенсуються невизначеними помилками, що впливають на інші стандарти. Стандарт, обраний для одноточкової стандартизації, має сигнал, менший, ніж передбачений рівнянням регресії, яке занижує k A і завищує C A.
Зовнішня стандартизація дозволяє аналізувати серію зразків за допомогою однієї калібрувальної кривої. Це важлива перевага, коли у нас є багато зразків для аналізу. Не дивно, що багато найбільш поширених кількісних аналітичних методів використовують зовнішню стандартизацію.
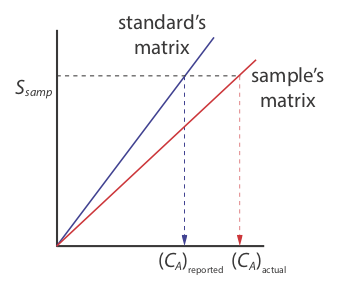
Однак існує серйозне обмеження зовнішньої стандартизації. Коли ми визначаємо значення k A за допомогою Equation\ ref {5.5}, аналіт присутній у матриці зовнішнього стандарту, яка зазвичай є набагато простішою матрицею, ніж матриця наших зразків. Коли ми використовуємо зовнішню стандартизацію, ми припускаємо, що матриця не впливає на значення k A. Якщо це не так, то вводимо в наш аналіз пропорційну детермінантну похибку. Це не так на малюнку Template:index, наприклад, де ми показуємо калібрувальні криві для аналіта в матриці зразка та в матриці стандарту. У цьому випадку використання калібрувальної кривої для зовнішніх стандартів призводить до негативної детермінантної помилки в повідомленій концентрації аналіту. Якщо ми очікуємо, що матричні ефекти важливі, то ми намагаємося відповідати матриці стандарту з матрицею зразка, процесу, відомого як відповідність матриці. Якщо ми не впевнені в матриці зразка, то ми повинні показати, що матричні ефекти незначні або використовувати альтернативний метод стандартизації. Обидва підходи розглядаються в наступному розділі.
Матрицею зовнішніх стандартів на рис. Template:index, наприклад, є розбавленим аміаком. Оскільки\(\ce{Cu(NH3)4^{2+}}\) комплекс поглинає сильніше, ніж Cu 2 +, додавання аміаку збільшує величину сигналу. Якщо нам не вдасться додати таку ж кількість аміаку в наші зразки, то ми внесемо в наш аналіз пропорційну детермінантну похибку.
Стандартні доповнення
Уникнути ускладнення узгодження матриці стандартів з матрицею зразка можна, якщо провести стандартизацію в вибірці. Це відомо як метод стандартних доповнень.
Одномісний стандарт з доповненням
Найпростіша версія стандартного доповнення показана на рисунку Template:index. Спочатку додаємо порцію зразка, V o, в об'ємну колбу, розводимо її до обсягу, V f, і вимірюємо його сигнал, S samp. Далі ми додаємо другу ідентичну частину зразка до еквівалентної об'ємної колбі разом із шипом, V std, зовнішнього стандарту, концентрація якого становить C std. Після того, як розводимо шиповану пробу до такого ж кінцевого обсягу, заміряємо його сигнал, S шип.
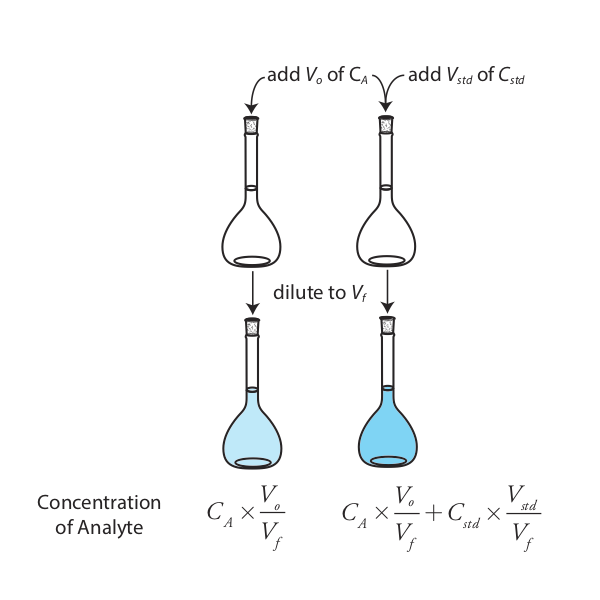
Наступні два рівняння пов'язують S samp і S спайк до концентрації аналіту, C A, у вихідному зразку.
\[S_{samp} = k_A C_A \frac {V_o} {V_f} \label{5.7}\]
\[S_{spike} = k_A \left( C_A \frac {V_o} {V_f} + C_{std} \frac {V_{std}} {V_f} \right) \label{5.8}\]
Поки V std невеликий щодо V o, вплив матриці стандарту на матрицю зразка незначний. За цих умов значення k A однакове в Рівнянні\ ref {5.7} та Equation\ ref {5.8}. Розв'язування обох рівнянь для k A і рівняння дає
який ми можемо вирішити для концентрації аналіту, C A, у вихідному зразку.
Третій спектрофотометричний метод кількісного аналізу Pb 2+ в крові дає S samp 0,193 при розведенні 1,00 мл зразка крові до 5,00 мл. Другий зразок крові 1,00 мл шипують 1,00 мл зовнішнього стандарту 1560-ppb Pb 2 + і розбавляють до 5,00 мл, що дає S-шип 0,419. Яка концентрація Pb 2 + в вихідному зразку крові?
Рішення
Ми починаємо з внесення відповідних замін в Equation\ ref {5.9} і рішення для C A. Зверніть увагу, що всі томи повинні бути в однакових одиницях; таким чином, ми спочатку приховаємо V std від 1.00 mL до\(1.00 \times 10^{-3} \text{ mL}\).
\[\frac {0.193} {C_A \frac {1.00 \text{ mL}} {5.00 \text{ mL}}} = \frac {0.419} {C_A \frac {1.00 \text{ mL}} {5.00 \text{ mL}} + 1560 \text{ ppb} \frac {1.00 \times 10^{-3} \text{ mL}} {5.00 \text{ mL}}} \nonumber\]
\[\frac {0.193} {0.200C_A} = \frac {0.419} {0.200C_A + 0.3120 \text{ ppb}} \nonumber\]
\[0.0386C_A + 0.0602 \text{ ppb} = 0.0838 C_A \nonumber\]
\[0.0452 C_A = 0.0602 \text{ ppb} \nonumber\]
\[C_A = 1.33 \text{ ppb} \nonumber\]
Концентрація Pb 2 + в вихідному зразку крові становить 1,33 ppb.
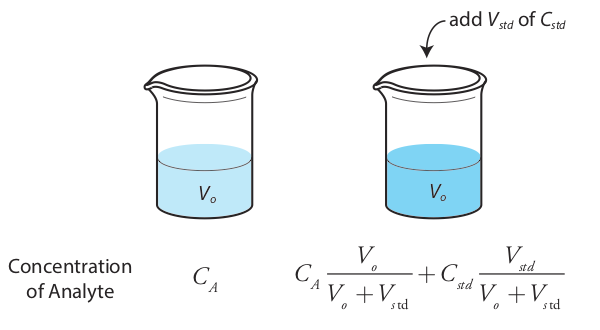
Також можна додати стандартне додавання безпосередньо до вибірки, вимірюючи сигнал як до, так і після спайка (Рисунок Template:index). У цьому випадку кінцевим об'ємом після стандартного додавання буде V o + V std і Equation\ ref {5.7}, Equation\ ref {5.8}, і Equation\ ref {5.9} стають
\[S_{samp} = k_A C_A \nonumber\]
Четвертий спектрофотометричний метод кількісного аналізу Pb 2+ в крові дає S samp 0,712 для зразка крові 5,00 мл. Після спайки зразка крові 5,00 мл зовнішнього стандарту 1560-ppb Pb 2 + вимірюється спайк S 1,546. Яка концентрація Pb 2 + в вихідному зразку крові?
Рішення
\[\frac {0.712} {C_A} = \frac {1.546} {C_A \frac {5.00 \text{ mL}} {5.005 \text{ mL}} + 1560 \text{ ppb} \frac {5.00 \times 10^{-3} \text{ mL}} {5.005 \text{ mL}}} \nonumber\]
\[\frac {0.712} {C_A} = \frac {1.546} {0.9990C_A + 1.558 \text{ ppb}} \nonumber\]
\[0.7113C_A + 1.109 \text{ ppb} = 1.546C_A \nonumber\]
\[C_A = 1.33 \text{ ppb} \nonumber\]
Концентрація Pb 2+ в вихідному зразку крові становить 1,33 ppb.
Кілька стандартних доповнень
Ми можемо адаптувати одноточкове стандартне доповнення до множинного стандартного додавання, підготувавши серію зразків, які містять зростаючі обсяги зовнішнього стандарту. На малюнку Template:index показано два способи побудови стандартної калібрувальної кривої додавання на основі Equation\ ref {5.8}. На малюнку Template:index a ми будуємо шип S відносно обсягу шипів, V std. Якщо k A постійна, то калібрувальна крива - пряма. Легко показати, що х -перехоплення еквівалентно — C A V o /C std.
Починаючи з Equation\ ref {5.8} показують, що рівняння на малюнку Template:index} a для нахилу, y -перехоплення та x -перехоплення правильні.
Рішення
Ми починаємо з перезапису Equation\ ref {5.8} як
\[S_{spike} = \frac {k_A C_A V_o} {V_f} + \frac {k_A C_{std}} {V_f} \times V_{std} \nonumber\]
який у вигляді рівняння для прямої
\[y = y\text{-intercept} + \text{slope} \times x\text{-intercept} \nonumber\]
де y - S шип, а х - V std. Нахил лінії, отже, дорівнює k A C std/V f, а y -перехоплення дорівнює k A C A В о /В ф. X -intercept - це значення x, коли y дорівнює нулю, або
\[0 = \frac {k_A C_A V_o} {V_f} + \frac {k_A C_{std}} {V_f} \times x\text{-intercept} \nonumber\]
\[x\text{-intercept} = - \frac {k_A C_A V_o / V_f} {K_A C_{std} / V_f} = - \frac {C_A V_o} {C_{std}} \nonumber\]
Починаючи з рівняння\ ref {5.8} показують, що рівняння на малюнку Template:index b для нахилу, y -перехоплення та x -перехоплення правильні.
- Відповідь
-
Почнемо з рівняння\ ref {5.8}
\[S_{spike} = k_A \left( C_A \frac {V_o} {V_f} + C_{std} \frac {V_{std}} {V_f} \right) \nonumber\]
переписуючи його як
\[S_{spike} = \frac {k_A C_A V_o} {V_f} + k_A \left( C_{std} \frac {V_{std}} {V_f} \right) \nonumber\]
який у вигляді лінійного рівняння
\[y = y\text{-intercept} + \text{slope} \times x\text{-intercept} \nonumber\]
де y - S шип, а х - C std \(\times\)V std/V f. Нахил лінії, отже, дорівнює k A, а y -перехоплення - k A C A V o /V f. X -intercept - це значення x, коли y дорівнює нулю, або
\[x\text{-intercept} = - \frac {k_A C_A V_o/V_F} {k_A} = - \frac {C_A V_o} {V_f} \nonumber\]
Оскільки ми знаємо об'єм вихідного зразка, V o, і концентрацію зовнішнього стандарту, C std, ми можемо обчислити концентрації аналіта з x -перехоплення множинних стандартних доповнень.
П'ятий спектрофотометричний метод кількісного аналізу Pb 2+ в крові використовує багатоточкове стандартне додавання на основі Equation\ ref {5.8}. Вихідний зразок крові має об'єм 1,00 мл, а стандарт, який використовується для шипування зразка, має концентрацію 1560 ppb Pb 2 +. Всі зразки були розведені до 5,00 мл перед вимірюванням сигналу. Калібрувальна крива S спайка проти V std має наступне рівняння
\[S_{spike} = 0.266 + 312 \text{ mL}^{-1} \times V_{std} \nonumber\]
Яка концентрація Pb 2+ в вихідному зразку крові?
Рішення
Щоб знайти x -перехоплення, ми встановимо S шип рівний нулю.
\[S_{spike} = 0.266 + 312 \text{ mL}^{-1} \times V_{std} \nonumber\]
Розв'язуючи для V std, отримаємо значення\(-8.526 \times 10^{-4} \text{ mL}\) для x -перехоплення. Підставляємо значення x -перехоплення у рівняння з рисунка Template:index a
\[-8.526 \times 10^{-4} \text{ mL} = - \frac {C_A V_o} {C_{std}} = - \frac {C_A \times 1.00 \text{ mL}} {1560 \text{ ppb}} \nonumber\]
а рішення для С А дає концентрацію Pb 2 + в зразку крові як 1,33 ppb.
На малюнку Template:index показана стандартна крива калібрування доповнення для кількісного аналізу Mn 2 +. Кожен розчин містить 25,00 мл вихідного зразка і 0, 1,00, 2,00, 3,00, 4,00 або 5,00 мл зовнішнього стандарту 100,6 мг/л Mn 2 +. Всі стандартні зразки додавання були розведені до 50,00 мл водою перед читанням поглинання. Рівняння для калібрувальної кривої на рисунку Template:index a дорівнює
\[S_{std} = 0.0854 \times V_{std} + 0.1478 \nonumber\]
Яка концентрація Mn 2 + в цій пробі? Порівняйте свою відповідь з даними на рисунку Template:index b, для яких є калібрувальна крива
\[S_{std} = 0.425 \times C_{std}(V_{std}/V_f) + 0.1478 \nonumber\]
- Відповідь
-
Використовуючи калібрувальне рівняння з рисунка Template:index a, ми виявимо, що x -перехоплення
\[x\text{-intercept} = - \frac {0.1478} {0.0854 \text{ mL}^{-1}} = - 1.731 \text{ mL} \nonumber\]
Якщо включити цей результат в рівняння для x -перехоплення і вирішити для C A, то виявимо, що концентрація Mn 2 + дорівнює
\[C_A = - \frac {x\text{-intercept} \times C_{std}} {V_o} = - \frac {-1.731 \text{ mL} \times 100.6 \text{ mg/L}} {25.00 \text{ mL}} = 6.96 \text{ mg/L} \nonumber\]
Для малюнка Template:index b, x -перехоплення є
\[x\text{-intercept} = - \frac {0.1478} {0.0425 \text{ mL/mg}} = - 3.478 \text{ mg/mL} \nonumber\]
і концентрація Mn 2 + становить
\[C_A = - \frac {x\text{-intercept} \times V_f} {V_o} = - \frac {-3.478 \text{ mg/mL} \times 50.00 \text{ mL}} {25.00 \text{ mL}} = 6.96 \text{ mg/L} \nonumber\]
Оскільки ми будуємо стандартну криву калібрування доповнення в зразку, ми не можемо використовувати калібрувальне рівняння для інших зразків. Кожен зразок, таким чином, вимагає власних стандартних доповнень калібрувальної кривої. Це серйозний недолік, якщо у вас багато зразків. Наприклад, припустимо, вам потрібно проаналізувати 10 зразків за допомогою п'ятиточкової калібрувальної кривої. Для нормальної калібрувальної кривої потрібно проаналізувати всього 15 розчинів (п'ять стандартів і десять зразків). Якщо ви використовуєте метод стандартних доповнень, ви повинні проаналізувати 50 розчинів (кожен з десяти зразків аналізується п'ять разів, один раз перед шипами і після кожного з чотирьох шипів).
Використання стандартного доповнення для ідентифікації матричних ефектів
Ми можемо використовувати метод стандартних доповнень для перевірки зовнішньої стандартизації, коли узгодження матриці неможливо. Спочатку готуємо нормальну калібрувальну криву S std проти C std і визначаємо значення k A з її нахилу. Далі готуємо стандартну криву калібрування доповнень за допомогою Equation\ ref {5.8}, будуючи дані, як показано на малюнку Template:index b. Ухил цієї стандартної калібрувальної кривої доповнення забезпечує незалежне визначення k A. Якщо між двома значеннями k A немає суттєвої різниці, то ми можемо ігнорувати різницю між матрицею вибірки та матрицею зовнішніх стандартів. Коли значення k A значно відрізняються, то за допомогою нормальної калібрувальної кривої вводиться пропорційна визначальна похибка.
Внутрішні стандарти
Щоб використовувати зовнішню стандартизацію або метод стандартних доповнень, ми повинні вміти однаково ставитися до всіх зразків і стандартів. Коли це неможливо, точність та точність нашої стандартизації можуть постраждати. Наприклад, якщо наш аналіт знаходиться в летючому розчиннику, то його концентрація збільшиться, якщо ми втратимо розчинник до випаровування. Припустимо, у нас є зразок і стандарт з однаковими концентраціями аналіту і ідентичними сигналами. Якщо обидва відчувають однакові пропорційні втрати розчинника, то їх відповідні концентрації аналіту та сигналів залишаються ідентичними. Фактично, ми можемо ігнорувати випаровування, якщо зразки та стандарти відчувають еквівалентну втрату розчинника. Однак якщо ідентичний стандарт і зразок втрачають різну кількість розчинника, то їх відповідні концентрації та сигнали вже не рівні. У цьому випадку проста зовнішня стандартизація або стандартне додавання неможливе.
Ми все ще можемо завершити стандартизацію, якщо посилаємо сигнал аналіта на сигнал іншого виду, який ми додаємо до всіх зразків та стандартів. Вид, який ми називаємо внутрішнім стандартом, повинен відрізнятися від аналіта.
Оскільки аналіт і внутрішній стандарт отримують однакове лікування, на співвідношення їх сигналів не впливає відсутність відтворюваності в процедурі. Якщо розчин містить аналіт концентрації C A і внутрішній стандарт концентрації C IS, то сигнали, обумовлені аналітом, S A, і внутрішнім стандартом, S ІС, є
\[S_A = k_A C_A \nonumber\]
\[S_{IS} = k_{SI} C_{IS} \nonumber\]
де\(k_A\) і\(k_{IS}\) є чутливості для аналіту і внутрішнього стандарту відповідно. Прийняття співвідношення двох сигналів дає фундаментальне рівняння для внутрішньої стандартизації.
Оскільки K є співвідношенням чутливості аналіта та чутливості внутрішнього стандарту, не потрібно самостійно визначати значення для k A або k IS.
Одномісний внутрішній стандарт
При одноточковій внутрішній стандартизації ми готуємо єдиний стандарт, який містить аналіт і внутрішній стандарт, і використовуємо його для визначення значення K в Equation\ ref {5.12}.
Стандартизувавши метод, концентрація аналіта задається
\[C_A = \frac {C_{IS}} {K} \times \left( \frac {S_A} {S_{IS}} \right)_{samp} \nonumber\]
Шостий спектрофотометричний метод кількісного аналізу Pb 2+ в крові використовує Cu 2 + як внутрішній стандарт. Стандарт, який становить 1,75 ppb Pb 2 + і 2,25 ppb Cu 2 + дає співвідношення (S A/S IS) std 2,37. Зразок крові з шипами з однаковою концентрацією Cu 2 + дає коефіцієнт сигналу, (S A/S IS) samp, 1.80. Яка концентрація Pb 2 + в зразку крові?
Рішення
Рівняння\ ref {5.13} дозволяє обчислити значення K, використовуючи дані для стандарту
\[K = \left( \frac {C_{IS}} {C_A} \right)_{std} \times \left( \frac {S_A} {S_{IS}} \right)_{std} = \frac {2.25 \text{ ppb } \ce{Cu^{2+}}} {1.75 \text{ ppb } \ce{Pb^{2+}}} \times 2.37 = 3.05 \frac {\text{ppb } \ce{Cu^{2+}}} {\text{ppb } \ce{Pb^{2+}}} \nonumber\]
Концентрація Pb 2 +, отже, становить
\[C_A = \frac {C_{IS}} {K} \times \left( \frac {S_A} {S_{IS}} \right)_{samp} = \frac {2.25 \text{ ppb } \ce{Cu^{2+}}} {3.05 \frac {\text{ppb } \ce{Cu^{2+}}} {\text{ppb } \ce{Pb^{2+}}}} \times 1.80 = 1.33 \text{ ppb } \ce{Pb^{2+}} \nonumber\]
Кілька внутрішніх стандартів
Одноточкова внутрішня стандартизація має ті ж обмеження, що і одноточкова нормальна калібрування. Для побудови внутрішньої стандартної калібрувальної кривої ми готуємо ряд стандартів, кожен з яких містить однакову концентрацію внутрішнього стандарту та різні концентрації аналіту. У цих умовах калібрувальна крива (S A/S IS) std проти C A є лінійною з нахилом K/ C IS .
Хоча звичайна практика полягає в підготовці стандартів так, щоб кожен містив ідентичну кількість внутрішнього стандарту, це не є вимогою.
Сьомий спектрофотометричний метод кількісного аналізу Pb 2+ в крові дає лінійну внутрішню норму калібрувальної кривої, для якої
\[\left( \frac {S_A} {S_{IS}} \right)_{std} = (2.11 \text{ ppb}^{-1} \times C_A) - 0.006 \nonumber\]
Що таке ppb Pb 2 + в зразку крові, якщо (S A/S IS) samp дорівнює 2,80?
Рішення
Для визначення концентрації Pb 2 + в зразку крові замінюємо (S A/S IS) std в калібрувальному рівнянні на (S A/ S IS) samp і вирішити для C A.
\[C_A = \frac {\left( \frac {S_A} {S_{IS}} \right)_{samp} + 0.006} {2.11 \text{ ppb}^{-1}} = \frac {2.80 + 0.006} {2.11 \text{ ppb}^{-1}} = 1.33 \text{ ppb } \ce{Pb^{2+}} \nonumber\]
Концентрація Pb 2 + в зразку крові становить 1,33 ppb.
За деяких обставин неможливо підготувати стандарти так, щоб кожен містив однакову концентрацію внутрішнього стандарту. Це той випадок, наприклад, коли ми готуємо зразки по масі замість обсягу. Ми все ще можемо підготувати калібрувальну криву, однак, шляхом побудови графіка\((S_A / S_{IS})_{std}\) проти C A/C IS, даючи лінійну калібрувальну криву з нахилом K.
Ви можете задатися питанням, чи можна включити внутрішній стандарт у метод стандартних доповнень для виправлення як матричних ефектів, так і для неконтрольованих варіацій між зразками; ну, відповідь так, як описано в статті «Стандартний аналіз розведення», повне посилання на який є Джонс, В.Б.; Донаті, Г.Л.; Калловей, К.П.; Джонс, Б.Т. анал. Хім. 2015, 87, 2321-2327.
