22.3: Електродні потенціали

Ми почали цю главу з вивчення електрохімічної осередку на малюнку 22.1.1, де\(\ce{Zn(s)}\) окислюється до\(\ce{Zn^{2+}(aq)}\) і зводиться до\(\ce{Ag(s)}\), як показано\(\ce{Ag^{+}(aq)}\) наступною реакцією.

\[2 \mathrm{Ag}(s)+\mathrm{Zn}^{2+}(\mathrm{aq}) \rightleftharpoons \mathrm{Zn}(s)+2 \mathrm{Ag}^{+}(a q) \nonumber \]

Реакція протікає як написано, оскільки зменшення Ag ⁺ (aq) до Ag (s)

\[\mathrm{Ag}^{+}(a q)+e^{-} \rightleftharpoons \mathrm{Ag}(s) \label{red_ag} \]

є більш термодинамічно сприятливим, ніж зниження\(\ce{Zn^{2+}(aq)}\) до\(\ce{Zn(s)}\)

\[\text{ Zn}^{2+}(aq)+2 e^{-} \rightleftharpoons \mathrm{Zn}(s) \label{red_zn} \]

Але, як ми знаємо, що це правда? У цьому розділі ми відповімо на це питання, уважно розглянувши електродні потенціали.

Природа електродних потенціалів

Потенціал електрохімічної комірки - це різниця між потенціалом на катоді та потенціалом на аноді\(E_\text{anode}\), де обидва потенціали визначаються через реакцію відновлення (і називаються відновними потенціалами); таким чином\(E_\text{cathode}\)

\[E_\text{cell} = E_\text{cathode} - E_\text{anode} \label{cell_pot} \]

\[\mathrm{H}^{+}(a q)+e^{-}=\frac{1}{2} \mathrm{H}_{2}(g) \label{she} \]

яка є реакцією, яка визначає стандартний водневий електрод, або SHE.

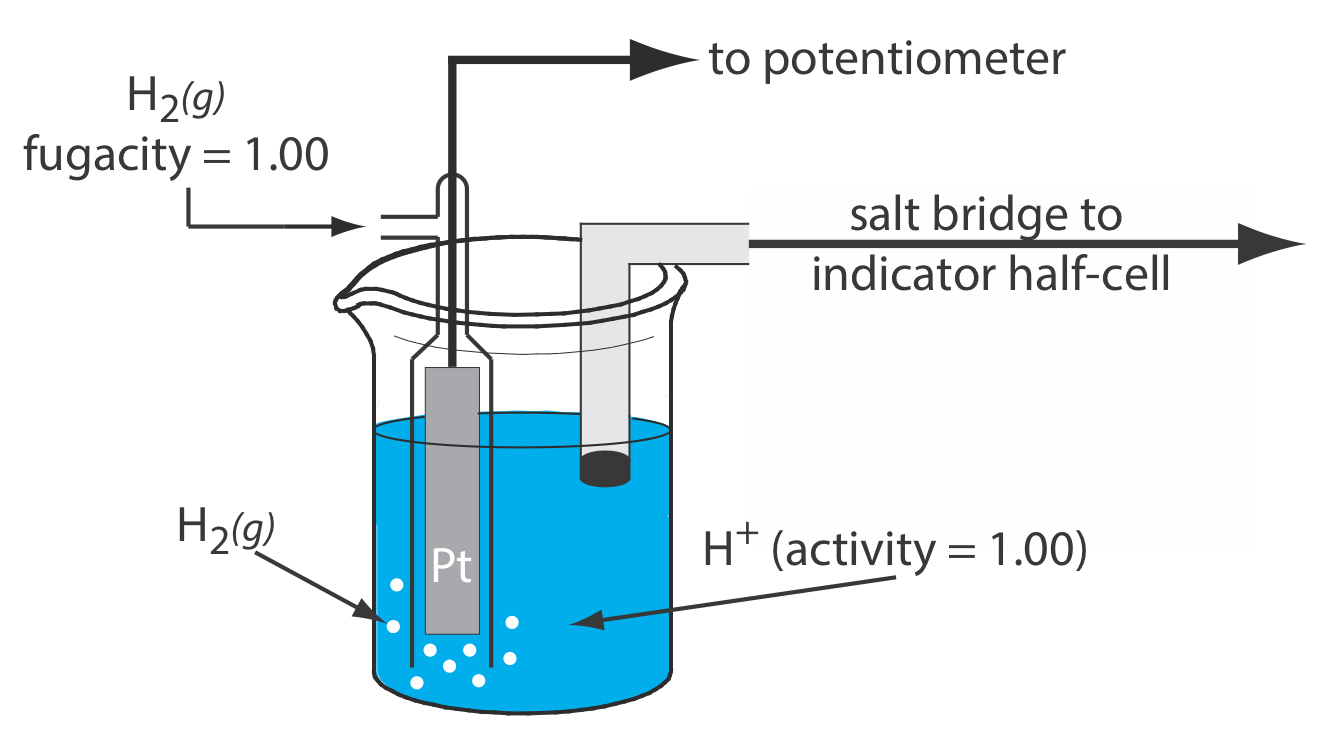
Стандартний водневий електрод (SHE)

SHE складається з електрода Pt, зануреного в розчин, в якому активність іона водню становить 1,00 і в якому парціальний тиск Н ₂ (г) становить 1,00 атм (рис.\(\PageIndex{1}\)). Звичайний соляний міст з'єднує SHE з індикатором напівосередку. Коротке позначення руки для стандартного водневого електрода є

\[\text{Pt}(s), \text{ H}_{2}\left(g, f_{\mathrm{H}_{2}}=1.00\right) | \text{ H}^{+}\left(a q, a_{\mathrm{H}^{+}}=1.00\right) \| \label{she_cell} \]

а потенціал стандартного стану для реакції\ ref {she} становить, за визначенням, 0.000 В при всіх температурах.

Малюнок\(\PageIndex{1}\). Принципова схема, що показує стандартний водневий електрод.

Практичні довідкові електроди

Хоча стандартний водневий електрод є стандартом, на який посилаються всі інші потенціали, він не є практичним для звичайного використання, оскільки його важко підготувати та підтримувати. Замість цього ми використовуємо один з декількох інших опорних електродів. Двома найпоширенішими з цих альтернативних еталонних електродів є каломель, або електрод Hg/Hg _{2 Cl 2}, який заснований на наступній окислювально-відновній парі між Hg _{2 Cl 2} і Hg (каломель - загальна назва Hg ₂ Cl ₂)

\[\mathrm{Hg}_{2} \mathrm{Cl}_{2}(s)+2 e^{-}\rightleftharpoons2 \mathrm{Hg}(l)+2 \mathrm{Cl}^{-}(a q) \nonumber \]

і опорний електрод Ag/AgCl, який заснований на зниженні AgCl до Ag

\[\operatorname{AgCl}(s)+e^{-} \rightleftharpoons \mathrm{Ag}(s)+\mathrm{Cl}^{-}(a q) \nonumber \]

Більш детальний огляд цих двох опорних електродів знаходиться в главі 23.1.

Визначення електродного потенціалу

Для визначення потенціалу зниження Zn ^{2 +} (aq) до Zn (s) зробимо його катодом в наступній електрохімічній комірці

\[\text{Pt}(s), \text{ H}_{2}\left(g, P_{\mathrm{H}_{2}}=1.00\right) | \text{ H}^{+}\left(a q, a_{\mathrm{H}^{+}}=1.00\right) \| \ce{Zn^{2+}}\left(a q, a_{\mathrm{Zn}^{2+}}=x\right) | \ce{Zn}(s) \label{she_zn} \]

де x - активність Zn ^{2 +} в його напівклітині. Наприклад, коли\(a_{\mathrm{Zn}^{2+}} = 1.00\), потенціал електрохімічної клітини є\(-0.763 \text{V}\). Якщо ми виявимо, що потенціал для електрохімічної клітини

\[\ce{Zn}(s) | \ce{Zn^{2+}} (aq, a_{\mathrm{Zn}^{2+}} = 1.00) \| \ce{Ag+} (aq, a_{\mathrm{Ag}^{+}} = 1.00) | \ce{Ag}(s) \nonumber \]

це +1,562 В, то знаючи, що

\[E_{cell} = E_{\ce{Ag+} / \ce{Ag}} - E_{\ce{Zn^{2+}} / \ce{Zn}} = E_{\ce{Ag+} / \ce{Ag}} - (-0.763 \text{V}) \nonumber \]

дає\(E_{\ce{Ag+} / \ce{Ag}} = +0.799\). Таким чином ми можемо побудувати таблиці потенціалів для окремих напівреакцій.

Угода про підписання електродних потенціалів

У розділі 22.2 ми відзначили наступний зв'язок між електрохімічним потенціалом та вільною енергією Гіббса,\(E\)\(\Delta G\)

\[\Delta G = - n F E \label{dg} \]

який говорить нам про те, що позитивний потенціал відповідає термодинамічно сприятливій реакції. Знання того, що потенціал електрохімічної комірки в рівнянні\ ref {she_zn}\(-0.763 \text{V}\) говорить нам про те, що зменшення Zn ^{2 +} (aq) до Zn (s) не є термодинамічно сприятливим щодо зменшення H ⁺ (aq) до H 2 (г); тобто ми не очікуємо реакції

\[\ce{Zn^{2+}}(aq) + \ce{H2}(g) \rightleftharpoons 2 \ce{H+}(aq) + \ce{Zn}(s) \label{zn_h} \]

відбуватися; однак, з потенціалом +0,799 В, ми очікуємо реакції

\[2 \ce{Ag+}(aq) + \ce{H2}(g) \rightleftharpoons 2 \ce{H+}(aq) + 2 \ce{Ag}(s) \label{ag_h} \]

відбуватися. Або, дивлячись на це по-іншому, ми очікуємо, що Zn (s), але не Ag (s), розчиниться в кислоті.

Вплив активності на електродні потенціали

У розділі 22.2 ми написали рівняння Нернста для реакції

\[\mathrm{Zn}(s)+2 \mathrm{Ag}^{+}(a q) \rightleftharpoons 2 \mathrm{Ag}(s)+\mathrm{Zn}^{2+}(\mathrm{aq}) \label{net_rxn} \]

в перерахунку на концентрації Zn ^{2 +} (aq) і Ag ⁺ (aq)

\[E = E^{\circ} - \frac{0.05916}{2} \log \frac {\left[ \ce{Zn^{2+}} \right]} {\left[ \ce{Ag+} \right]^2} \label{zn_ag_conc} \]

Хоча бувають випадки, коли ми будемо писати рівняння Нернста з точки зору концентрацій, термодинамічні функції більш правильно записані з точки зору діяльності іонів. В ідеальних умовах окремі іони і молекули газів поводяться як самостійні частинки. Коли це правда, то активність та концентрація іона рівні, і ми можемо записати рівняння Нернста, використовуючи концентрації; за інших умов рівняння Нернста правильніше записано з точки зору діяльності

\[E = E^{\circ} - \frac{0.05916}{2} \log \frac {a_{\ce{Zn^{2+}}}} {\left( a_{\ce{Ag+}} \right)^2} \label{zn_ag_activity} \]

де\(a_{\ce{Zn^{2+}}}\) і\(a_{\ce{Ag+}}\) знаходяться діяльність Zn ^{2 +} і Ag ⁺. Рівняння\ ref {zn_ag_activity} показує нам, як змінюється потенціал у міру зміни діяльності Zn ^{2 +} та Ag ⁺.

Якщо ви не знайомі з діяльністю або вам потрібно нагадування про взаємозв'язок між активністю та концентрацією, перегляньте додаток у розділі 35.7, де пояснюється, що таке діяльність, чому важливо розрізняти активність та концентрацію, а також коли розумно використовувати концентрації в місце діяльності.

Стандартний електродний потенціал\(E^{\circ}\)

Стандартний електродний потенціал\(E^{\circ}\), для напівреакції - це потенціал, коли всі види присутні при одиничній активності або, для газів, одиничній неміцності. Його значення не залежить від того, як ми вирішили записати напівреакцію; тобто стандартний потенціал стану для зниження Ag ⁺ (aq) до Ag (s), який є катодом в електрохімічній комірці на малюнку 22.1.1, становить +0,799 В чи записуємо напівреакцію як

\[\ce{Ag+}(aq) + e^{-} \rightleftharpoons \ce{Ag}(s) \label{ag1} \]

або як

\[2 \ce{Ag+}(aq) + e^{-} \rightleftharpoons 2 \ce{Ag}(s) \label{ag2} \]

На перший погляд це здається контрінтуїтивним; однак, якщо обчислити потенціал, коли активність Ag+ становить 0,50, ми отримаємо

\[E = E^{\circ} - \frac{0.05916}{1} \log \frac{1}{a_{\ce{Ag+}}} = 0.799 - \frac{0.05916}{1} \log \frac{1}{0.50} = 0.781 \text{V} \nonumber \]

при використанні реакції\ ref {ag1}, і

\[E = E^{\circ} - \frac{0.05916}{2} \log \frac{1}{(a_{\ce{Ag+}})^2} = 0.799 - \frac{0.05916}{2} \log \frac{1}{0.50^2} = 0.781 \text{V} \nonumber \]

У додатку до глави 35.8 наведена таблиця стандартних потенціалів відновлення стану для найрізноманітніших напівреакцій при 298 К.

Деякі обмеження використання стандартних електродних потенціалів

Хоча стандартні електродні потенціали цінні, вони є декількома важливими обмеженнями для їх використання, які ми викладемо тут.

Заміна концентрації на діяльність

Одним з важливих обмежень є те, що рівняння Нернста визначається з точки зору активності іонів замість їх концентрацій. Хоча легко приготувати розчин, для якого концентрація Na ⁺ становить 0,100 М, використовуючи NaCl - просто зважте 5,844 г NaCl і розчинити в 1,00 л води - набагато складніше приготувати розчин, для якого активність Na ⁺ становить 0,100. З цієї причини в розрахунках ми зазвичай підставляємо концентрації для діяльності при використанні рівняння Нернста. Це спрощення, як правило, добре для розбавлених розчинів, де різниця між діяльністю та концентраціями невелика.

Вплив інших реакцій рівноваги

Стандартний потенціал стану говорить нам про рівноважне положення окисно-відновної реакції напівреакції в стандартних умовах стану. Якщо один або кілька видів в напівреакції беруть участь в інших рівноважних реакціях, то ці реакції будуть впливати на величину стандартного потенціалу. Наприклад, Fe ^{2 +} і Fe ^{3 +} утворюють різноманітні метало-лігандні комплекси з Cl ^— що пояснює,\(E_{\ce{Fe^{3+}}/\ce{Fe^{2+}}}^{\circ}\) чому 0,771 при відсутності хлорид-іона, але становить 0,70 в 1 М HCl.

Формальні потенціали

Одним із способів компенсації використання концентрацій та парціальних тисків замість діяльності та невимушеності та компенсації інших реакцій рівноваги є заміна потенціалів стандартного стану\(E^{\circ}\) формальним потенціалом\(E^{\circ \prime}\), який вимірюється за допомогою концентрацій 1,00 для іонів, парціальний тиск 1,00 для газів, а для певної концентрації інших реагентів. ^{У наведеній нижче таблиці, яка адаптована з додатка в розділі 35.8, наведені формальні потенціали для напівреакції Fe 3 +/Fe 2 + в п'яти різних розчинниках.}

залізо	\(E^{\circ}\)(V)	\(E^{\circ \prime}\)(V)
\(\ce{Fe^{3+}} + e^{-} \rightleftharpoons \ce{Fe^{2+}}\)	\ (E^ {\ circ}\) (V) ">0.771	\ (E^ {\ circ\ прайм}\) (V) "> 0,70 в 1 М\(\ce{HCl}\) 0,767 в 1 М\(\ce{HClO4}\) 0,746 в 1 М\(\ce{HNO3}\) 0,68 в 1 М\(\ce{H2SO4}\) 0,44 в 0,3 Мб\(\ce{H3PO4}\)

Швидкість реакції

Зниження Fe ^{3 +} до Fe ^{2 +} споживає електрон, який витягується з електрода. Окислення іншого виду, можливо, розчинника, на другому електроді є джерелом цього електрона. Оскільки зменшення Fe ^{3 +} до Fe ^{2 +} споживає один електрон, потік електронів між електродами - іншими словами, струм - є мірою швидкості, з якою Fe ^{3 +} зменшується. Одним з важливих наслідків цього спостереження є те, що струм дорівнює нулю, коли реакція\(\text{Fe}^{3+}(aq) \rightleftharpoons \text{ Fe}^{2+}(aq) + e^-\) знаходиться в рівновазі. Якщо окислювально-відновна напівреакція не може підтримувати рівновагу, оскільки реакція в одному напрямку занадто повільна, то ми не можемо виміряти значущий стандартний потенціал стану.