6.1: Випадкові величини та ймовірності

Last updated
Save as PDF

Page ID: 98751

Paul Pfeiffer
Rice University

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Імовірність пов'язує з подією число, яке вказує на ймовірність виникнення цієї події на будь-якому судовому розгляді. Подія моделюється як сукупність тих можливих результатів експерименту, які задовольняють властивість або пропозицію, що характеризує подію.

Найчастіше кожен результат характеризується числом. Експеримент виконується. Якщо результат спостерігається як фізична величина, розмір цієї кількості (у встановлених одиницях) є фактично спостережуваним суб'єктом. У багатьох нечислових випадках зручно привласнювати число кожному результату. Наприклад, в експерименті з гортання монет «голова» може бути зображена 1, а «хвіст» - 0. У випробуванні Бернуллі успіх може бути представлений 1, а невдача - 0. У послідовності випробувань нас може зацікавити кількість успіхів у послідовності випробувань$n$ компонентів. Можна призначити окремий номер кожній картці в колоді гральних карт. Спостереження за результатом вибору карти могли бути записані в розрізі окремих номерів. У кожному конкретному випадку асоційоване число стає властивістю результату.

Випадкові величини як функції

Розглянемо в цьому розділі реальні випадкові величини (тобто дійсні випадкові величини). У розділі про випадкові вектори та спільні розподіли ми поширюємо поняття на векторні випадкові кількості. Фундаментальною ідеєю реальної випадкової величини є присвоєння дійсного числа кожному$\omega$ елементарному результату в базовому просторі$\Omega$. Таке присвоєння зводиться до визначення функції$X$, область якої дорівнює$\Omega$ і діапазон якої є підмножиною дійсної лінії R. Нагадаємо, що дійсна функція на домені (скажімо інтервал$I$ на дійсному рядку) характеризується присвоєнням дійсного числа$y$ кожному елементу$x$ (аргументу) в області. Для реальної функції дійсної змінної часто можна написати формулу або іншим чином вказати правило, що описує присвоєння значення кожному аргументу. За винятком особливих випадків, ми не можемо написати формулу для випадкової величини$X$. Однак випадкові величини мають деякі важливі загальні властивості функцій, які відіграють важливу роль у визначенні їх корисності.

Відображення та зворотні відображення

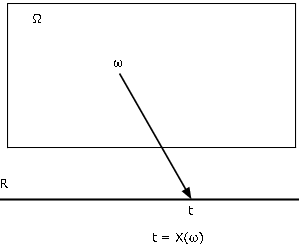
Існують різні способи характеристики функції. Напевно, найбільш корисним для наших цілей є відображення від домену$\Omega$ до кодомену R. Ми знаходимо діаграму відображення на малюнку 1 надзвичайно корисною для візуалізації основних закономірностей. Випадкова величина$X$, як відображення з базового простору$\Omega$ в дійсну лінію R, привласнює кожному елементу$\omega$ значення$t = X(\omega)$. Точка об'єкта$\omega$ зіставляється або переноситься в точку зображення$t$. Кожен$\omega$ зіставляється точно в одну$t$, хоча кілька$\omega$ можуть мати однакову точку зображення.

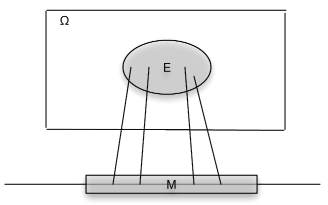
Малюнок 6.1. 1. Базова діаграма відображення$t = X(\omega)$.

З функцією$X$ як відображення пов'язані зворотне відображення$X^{-1}$ та зворотні зображення, які вона створює. $M$Дозволяти набір чисел на дійсному рядку. Під зворотним зображенням$M$ під відображенням$X$ ми маємо на увазі безліч всіх тих,$\omega \in \Omega$ які$M$ відображені в$X$ (див. Рис. Якщо$X$ не приймає значення в$M$, обернене зображення є порожнім набором (неможлива подія). Якщо$M$ включає діапазон$X$, (набір всіх можливих значень$X$), то зворотним зображенням буде весь базовий простір$\Omega$. Формально пишемо

$X^{-1} (M) = \{\omega: X(\omega) \in M\}$

Тепер ми припускаємо$X^{-1} (M)$, що набір,$\Omega$ підмножина, є подією для кожного$M$. Детальний розгляд цього твердження є темою теорії мір. На щастя, результати теорії вимірювань гарантують, що ми можемо зробити припущення для будь-якої$X$ підмножини$M$ реальної лінії, яка може зустрітися на практиці. Набір$X^{-1} (M)$ - це подія, яка$X$ приймає значення в$M$. Як події йому може бути призначена ймовірність.

Малюнок 6.1. 2. Е - зворотне зображення$X^{-1} (M)$.

Приклад$\PageIndex{1}$ Some illustrative examples

$I_E$де$E$ подія з ймовірністю$p$. Тепер$X$ приймає тільки два значення, 0 і 1. Подія, яка$X$ приймає значення 1, є множиною
$\{\omega: X(\omega) = 1\} = X^{-1} (\{1\}) = E$

так що$P(\{\omega: X(\omega) = 1\}) = p$. Це досить невиграшне позначення скорочується до$P(X = 1) = p$. Аналогічно,. Розглянемо будь-який набір$M$. Якщо ні 1, ні 0 знаходиться в$M$, то$X^{-1}(M) = \emptyset$ Якщо 0 знаходиться в$M$, а 1 - ні, то$X^{-1} (M) = E^c$ Якщо 1 знаходиться в$M$, а 0 - ні, то$X^{-1} (M) = E$ Якщо і 1, і 0 знаходяться$X^{-1} (M) = \Omega$ в$M$, то У цьому випадку клас всіх подій$X^{-1} (M)$ складається з події$E$, його доповнення$E^c$, неможлива подія$\emptyset$, і вірна подія$\Omega$.
Розглянемо послідовність випробувань$n$ Бернуллі, з$p$ ймовірністю успіху. $S_n$Дозволяти випадкова величина, значення якої є числом успіхів у послідовності випробувань$n$ компонентів. Потім, згідно з аналізом у розділі "Випробування Бернуллі та біноміальний розподіл"
$P(S_n = k) = C(n, k) p^k (1-p)^{n - k}$$0 \le k \le n$

Перш ніж розглядати подальші приклади, відзначимо загальну властивість зворотних зображень. Викладемо його через випадкову величину, яка відображає$\Omega$ дійсну пряму (див. Рис.

Збереження встановлених операцій

$X$Дозволяти відображення від$\Omega$ до дійсної лінії R. Якщо$M, M_i, i \in J$ множини дійсних чисел, з відповідними оберненими зображеннями$E$$E_i$, то

$X^{-1} (M^c) = E^c$,$X^{-1} (\bigcup_{i \in J} M_i) = \bigcup_{i \in J} E_i$ і$X^{-1} (\bigcap_{i \in J} M_i) = \bigcap_{i \in J} E_i$

Експертиза простих графічних прикладів демонструє правдоподібність цих закономірностей. Формальні докази зводяться до ретельного прочитання позначень. Центральними в структурі є факти, що кожен елемент ω відображається лише в одній точці зображення t і що зворотне зображення$M$ є сукупністю всіх тих,$\omega$ які відображені в точках зображення в$M$.

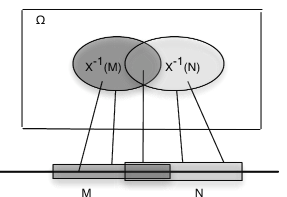
Малюнок 6.1. 3. Збереження множини операцій зворотними зображеннями.

Легким, але важливим наслідком загальних закономірностей є те, що зворотні зображення непоєднуваних також$M, N$ є неспільними. З цього випливає, що обернене нероз'єднаного союзу$M_i$ - це неспільний союз окремих обернених зображень.

Приклад$\PageIndex{2}$ Events determined by a random variable

Розглянемо, знову ж таки, випадкову$S_n$ величину, яка підраховує кількість успіхів у послідовності випробувань$n$ Бернуллі. Нехай$n = 10$ і$p = 0.33$. Припустимо, ми хочемо визначити ймовірність$P(2 < S_{10} \le 8)$. Нехай$A_k = \{\omega: S_{10} (\omega) = k\}$, які ми зазвичай скорочуємо до$A_k = \{S_{10} = k\}$. Тепер$A_k$ формуємо розділ, оскільки ми не можемо мати$\omega \in A_k$ і$\omega \in A_k$$j \ne k$ (тобто для будь-якого$\omega$, ми не можемо мати два значення для$S_n (\omega)$). Тепер,

$\{2 < S_{10} \le 8\} = A_3 \bigvee A_4 \bigvee A_5 \bigvee A_6 \bigvee A_7 \bigvee A_8$

оскільки$S_{10}$ приймає значення більше 2, але не більше 8, якщо воно приймає одне з цілих значень від 3 до 8. За адитивності ймовірності,

Масоперенесення та індукований розподіл ймовірностей

Через абстрактну природу базового простору і класу подій ми обмежені в видах розрахунків, які можуть бути виконані осмислено з ймовірностями на базовому просторі. Ми представляємо імовірність як масу, розподілену на базовому просторі, і візуалізуємо це за допомогою загальних діаграм Венна та мінтермальних карт. Тепер ми думаємо про відображення від$\Omega$ до R як створення точкового перенесення маси ймовірності до реальної лінії. Зробити це можна наступним чином:

До будь-якої множини$M$ на реальному рядку призначте масу ймовірності$P_X(M) = P(X^{-1}(M))$

Очевидно, що$P_X(M) \ge 0$ і$P_X$ (R)$= P(\Omega) = 1$. А через збереження множини операцій зворотним відображенням

$P_X(\bigvee_{i = 1}^{\infty} M_i) = P(X^{-1}(\bigvee_{i = 1}^{\infty} M_i)) = P(\bigvee_{i = 1}^{\infty} X^{-1}(M_i)) = \sum_{i = 1}^{\infty} P(X^{-1}(M_i)) = \sum_{i = 1}^{\infty} P_X(M_i)$

Це означає, що$P_X$ має властивості міри ймовірності, визначеної на підмножині дійсної лінії. Деякі результати теорії вимірювань показують, що ця ймовірність визначена однозначно на класі підмножин R, який включає будь-яку множину, яка зазвичай зустрічається у додатках. Домігся точкового перенесення апарату ймовірностей на реальну пряму таким чином, щоб ми могли проводити розрахунки щодо випадкової величини$X$. Ми називаємо$P_X$ міру ймовірності, індуковану X. Його важливість полягає в тому, що$P(X \in M) = P_X(M)$. Таким чином, щоб визначити ймовірність того, що випадкова величина X прийме значення в множині M, ми визначаємо, скільки індукованої маси ймовірності знаходиться в множині M. Ця передача виробляє те, що називається розподілом ймовірностей для X. У розділі «Функції розподілу та щільності» ми розглянемо корисні способи опису розподілу ймовірностей, індукованого випадковою величиною. Переходимо спочатку до спеціального класу випадкових величин.

Прості випадкові величини

Детально розглянуто випадкові величини, які мають лише скінченну множину можливих значень. Вони називаються простими випадковими величинами. При цьому термін «простий» вживається в особливому, технічному сенсі. Важливість простих випадкових величин спирається на два факти. З одного боку, на практиці можна виділити лише кінцевий набір можливих значень для будь-якої випадкової величини. Крім того, будь-яка випадкова величина може бути наближена так само близько, як задоволена простою випадковою величиною. Коли була розглянута структура і властивості простих випадкових величин, переходимо до більш загальних випадків. Багато властивостей простих випадкових величин поширюються на загальний випадок за допомогою процедури наближення.

Представлення за допомогою індикаторних функцій

Для того, щоб чітко і точно розібратися з простими випадковими величинами, ми повинні знайти відповідні способи їх вираження аналітично. Робимо це за допомогою індикаторних функцій. Зустрічаються три основні форми представлення. Це не взаємовиключні уявлення.

Стандартна або канонічна форма, в якій відображаються можливі значення і відповідні події. Якщо X набуває різних значень

$\{t_1, t_2, \cdot\cdot\cdot, t_n\}$з відповідними ймовірностями$\{p_1, p_2, \cdot\cdot\cdot, p_n\}$

а якщо$A_i = \{X = t_i\}$, для$1 \le i \le n$, то$\{A_1, A_2, \cdot \cdot\cdot, A_n\}$ це розділ (тобто на будь-якому судовому процесі відбувається саме одне з цих подій). Ми називаємо це розділом, визначеним (або, згенерованим) X. Ми можемо написати

$X = t_1 I_{A_1} + t_2 I_{A_2} + \cdot\cdot\cdot + t_n I_{A_n} = \sum_{i = 1}^{n} t_i I_{A_i}$

Якщо$X(\omega) = t_i$, то$\omega \in A_i$, так що$I_{A_i} (\omega) = 1$ і всі інші функції індикатора мають значення нуль. Таким чином, вираз підсумовування вибирає правильне значення$t_i$. Це вірно для будь-якого$t_i$, тому вираз представляє$X(\omega)$ для всіх$\omega$. Чіткий$\{A, B, C\}$ набір значень і відповідні ймовірності$\{p_1, p_2, \cdot\cdot\cdot, p_n\}$ складають розподіл для X. Розрахунки ймовірності для Х робляться в плані його розподілу. Однією з переваг канонічної форми є те, що вона відображає діапазон (набір значень), а якщо ймовірності$\{A, B, C, D\}$ відомі, то визначається розподіл. Зверніть увагу, що в канонічній формі, якщо один з$t_i$ має значення нуль, ми включаємо цей термін. Для деяких розподілів ймовірності це може бути, що$P(A_i) = 0$ для одного або декількох з$t_i$. У такому випадку ми називаємо ці значення нульовими значеннями, бо вони можуть виникати тільки з ймовірністю нуль, а значить, практично неможливі. У загальну формулювання включаємо можливі нульові значення, так як вони не впливають на будь-які обчислення ймовірності.

Приклад$\PageIndex{3}$ Successes in Bernoulli trials

Як показує аналіз випробувань Бернуллі та біноміального розподілу (див. Розділ 4.8), канонічна форма повинна бути

$S_n = \sum_{k = 0}^{n} k I_{A_k}$з$P(A_k) = C(n, k) p^{k} (1-p)^{n - k}$,$0 \le k \le n$

Для багатьох цілей бажана як теоретична, так і практична, канонічна форма. З одного боку, він відображає безпосередньо діапазон (тобто набір значень) випадкової величини. Розподіл складається з безлічі значень в$\{t_k: 1 \le k \le n\}$ парі з відповідним набором ймовірностей$\{p_k: 1 \le k \le n\}$, де$p_k = P(A_k) = P(X = t_k)$.

Проста випадкова величина X може бути представлена примітивною формою

$X = c_1 I_{C_1} + c_2 I_{C_2} + \cdot \cdot \cdot, c_m I_{C_m}$, де$\{C_j: 1 \le j \le m\}$ знаходиться перегородка

Зауваження

Якщо$\{C_j: 1 \le j \le m\}$ є незв'язаним класом, але$\bigcup_{j = 1}^{m} C_j \ne \Omega$, ми можемо додати подію$C_{m + 1} = [\bigcup_{j = 1}^{m} C_j]^c$ і призначити йому нуль.
Ми говоримо примітивну форму, так як уявлення не є унікальним. Будь-який з C _i може бути розділений, з однаковим значенням,$c_i$ пов'язаним з кожною сформованою підмножиною.
Канонічна форма - це особлива примітивна форма. Канонічна форма унікальна, і багато в чому нормативна.

Приклад$\PageIndex{4}$ Simple random variables in primitive form

Колесо обертається, що дає, на однаково ймовірній основі, цілі числа від 1 до 10. Нехай$C_i$ буде подія, на якій колесо зупиняється$i$,$1 \le i \le 10$. Кожному$P(C_i) = 0.1$. Якщо цифри 1, 4 або 7 з'являються, гравець втрачає десять доларів; якщо цифри 2, 5 або 8 з'являються, гравець нічого не отримує; якщо цифри 3, 6 або 9 з'являються, гравець отримує десять доларів; якщо число 10 з'являється, гравець втрачає один долар. Випадкова величина, що виражає результати, може бути виражена в примітивній формі як
$X = -10 I_{C_1} + 0 I_{C_2} + 10 I_{C_3} - 10 I_{C_4} + 0 I_{C_5} + 10 I_{C_6} - 10 I_{C_7} + 0 I_{C_8} + 10I_{C_9} - I_{C_{10}}$
У магазині є вісім предметів для продажу. Ціни складають $3.50, $5.00, $3.50, $7.50, $5.00, $5.00, $3.50 і $7,50 відповідно. Заходить клієнт. Вона купує один з предметів з ймовірностями 0,10, 0,15, 0,15, 0,20, 0,10 0,05, 0,10 0,15. Може бути записана випадкова величина, що виражає суму її покупки

$X = 3.5 I_{C_1} + 5.0 I_{C_2} + 3.5 I_{C_3} + 7.5 I_{C_4} + 5.0 I_{C_5} + 5.0 I_{C_6} + 3.5 I_{C_7} + 7.5 I_{C_8}$

Ми зазвичай маємо X, представлений в афінній формі, в якому випадкова величина представлена у вигляді афінної комбінації індикаторних функцій (тобто лінійна комбінація функцій індикатора плюс константа, яка може бути нульовою).

$X = c_0 + c_1 I_{E_1} + c_2 I_{E_2} + \cdot\cdot \cdot + c_m I_{E_m} = c_0 + \sum_{j = 1}^{m} c_j I_{E_j}$

У такому вигляді клас не обов'язково$\{E_1, E_2, \cdot\cdot\cdot, E_m\}$ є взаємовиключним, а коефіцієнти не відображають безпосередньо набір можливих значень. По суті,$E_i$ часто утворюють самостійний клас. Зауваження. Будь-яка примітивна форма - це особлива афінна форма, в якій$c_0 = 0$ і$E_i$ утворюють перегородку.

Приклад$\PageIndex{5}$

Розглянемо, знову ж таки, випадкову$S_n$ величину, яка підраховує кількість успіхів у послідовності випробувань$n$ Бернуллі. Якщо$E_i$ це подія успіху на$i$ судовому процесі, то одним природним способом висловити підрахунок є

$S_n = \sum_{i = 1}^{n} I_{E_i}$, з$P(E_i) = p$$1 \le i \le n$

Це афінна форма, з$c_0 = 0$ і$c_i =1$ для$1 \le i \le n$. У цьому випадку вони$E_i$ не можуть утворювати взаємовиключний клас, так як вони утворюють незалежний клас.

Події, породжені простою випадковою величиною: канонічна форма
Ми можемо охарактеризувати клас всіх обернених зображень, утворених простим випадковим з$X$ точки зору визначеного розділу. Розглянемо будь-який набір$M$ дійсних чисел. Якщо$t_i$ в діапазоні$X$ знаходиться в$M$, то кожна точка$\omega \in A_i$ відображає в$t_i$, отже, в$M$. Якщо множина$J$ є сукупністю індексів$i$ такі$t_i \in M$, що, то

Тільки ті точки$\omega$ на$A_M = \bigvee_{i \in J} A_i$ карті в$M$.

Отже, клас подій (тобто обернених зображень), що визначається$\emptyset$,$X$ складається з неможливої події$\Omega$, певної події та об'єднання будь-якого підкласу$A_i$ в розділі, визначеному$X$.

Приклад$\PageIndex{6}$ Events determined by a simple random variable

Припустимо, проста випадкова величина$X$ представлена в канонічному вигляді

$X = -2I_A - I_B + 0 I_C + 3I_D$

Тоді клас$\{A, B, C, D\}$ - це розділ, який визначається$X$ і діапазон$X$ is$\{-2, -1, 0, 3\}$.

Якщо$M$ інтервал [-2, 1], то значення -2, -1 і 0 знаходяться в$M$ і$X^{-1}(M) = A \bigvee B \bigvee C$.
Якщо$M$ множина (-2, -1]$\cup$ [1, 5], то значення -1, 3 знаходяться в$M$ і$X^{-1}(M) = B \bigvee D$.
Захід$\{X \le 1\} = \{X \in (-\infty, 1]\} = X^{-1} (M)$, де$M = (- \infty, 1]$. Оскільки значення -2, -1, 0 знаходяться в$M$, подія$\{X \le 1\} = A \bigvee B \bigvee C$.

Визначення розподілу

Визначення розділу, породженого простою випадковою величиною, зводиться до визначення канонічної форми. Потім розподіл завершується визначенням ймовірностей кожної події$A_k = \{X = t_k\}$.

З примітивної форми

Перш ніж записати загальну закономірність, розглянемо наочний приклад.

Приклад$\PageIndex{7}$ The distribution from a primitive form

Припустимо, що один елемент вибирається випадковим чином з групи з десяти елементів. Значення (у доларах) та відповідні ймовірності


$c_j$	2.00	1,50	2.00	2.50	1,50	1,50	1.00	2.50	2.00	1,50
$P(C_j)$	0,08	0,11	0,07	0,15	0,10	0,09	0,14	0,08	0,08	0,10

За допомогою огляду ми знаходимо чотири різних значення:$t _ 1 = 1.00$,$t_2 = 1.50$,$t_3 = 2.00$, і$t_4 = 2.50$. Значення 1,00 береться за$\omega \in C_7$, так що$A_1 = C_7$ і$P(A_1) = P(C_7) = 0.14$. Значення 1.50 береться за$\omega \in C_2, C_5, C_6, C_{10}$ так, щоб

$A_2 = C_2 \bigvee C_5 \bigvee C_6 \bigvee C_{10}$і$P(A_2) = P(C_2) + P(C_5) + P(C_6) + P(C_{10}) = 0.40$

Аналогічно

$P(A_3) = P(C_1) + P(C_3) + P(C_9) = 0.23$і$P(A_4) = P(C_4) + P(C_8) = 0.25$

Таким чином, розподіл для X


$k$	1.00	1,50	2.00	2.50
$P(X = k)$	0,14	0,40	0,23	0,23

Загальна процедура може бути сформульована наступним чином:

Якщо$X = \sum_{j = 1}^{m} c_j I_{c_j}$, ми ідентифікуємо набір різних значень у множині$\{c_j: 1 \le j \le m\}$. Припустимо, що такі є$t_1 < t_2 < \cdot\cdot\cdot < t_n$. Для будь-якого можливого значення$t_i$ в діапазоні визначте набір$J_i$ індексів$j$ таких, що$c_j = t_i$ Тоді терміни

$\sum_{J_i} c_j I_{c_j} = t_i \sum_{J_i} I_{c_j} = t_i I_{A_i}$, де$A_i = \bigvee_j \in J_i C_j$,

$P(A_i) = P(X = t_i) = \sum_{j \in J} P(C_j)$

Експертиза даної процедури показує, що існує дві фази:

Виділення та сортування різних значень$t_1, t_2, \cdot\cdot\cdot, t_n$
Додайте всі ймовірності, пов'язані з кожним значенням$t_i$, щоб визначити$P(X = t_i)$

Ми використовуємо m-функцію csort, яка виконує ці дві операції (див. Приклад 4 з «Розрахунки Minterms та MATLAB»).

Приклад$\PageIndex{8}$ Use of csort on Example 6.1.7

>> C = [2.00 1.50 2.00 2.50 1.50 1.50 1.00 2.50 2.00 1.50];  % Matrix of c_j
>> pc = [0.08 0.11 0.07 0.15 0.10 0.09 0.14 0.08 0.08 0.10]; % Matrix of P(C_j)
>> [X,PX] = csort(C,pc);     % The sorting and consolidating operation
>> disp([X;PX]')             % Display of results
    1.0000    0.1400
    1.5000    0.4000
    2.0000    0.2300
    2.5000    0.2300

Для цієї невеликої проблеми використання такого інструменту, як csort, насправді не потрібно. Але в багатьох проблемах з великими наборами даних m-функція csort дуже корисна.

Від афінної форми

$X$Припустимо, в афінній формі,

$X = c_0 + c_1 I_{E_1} + c_2 I_{E_2} + \cdot\cdot\cdot + c_m I_{E_m} = c_0 + \sum_{j = 1}^{m} c_j I_{E_j}$

Визначаємо ту чи іншу примітивну форму, визначаючи значення$X$ на кожному мінтермі, породженому класом$\{E_j: 1 \le j \le m\}$. Ми робимо це систематично, використовуючи мінтермальні вектори та властивості індикаторних функцій.

$X$є постійною на кожному мінтермі, породженому класом,$\{E_1, E_2, \cdot\cdot\cdot, E_m\}$ оскільки, як зазначається при обробці мінтермального розширення, кожна індикаторна функція$I_{E_i}$ є постійною на кожному мінтермі. Визначаємо$s_i$ значення$X$ на кожному мінтерміні$M_i$. Це описується$X$ в особливій примітивній формі

$X = \sum_{k = 0}^{2^m - 1} s_i I_{M_i}$, з$P(M_i) = p_i$,$0 \le i \le 2^m - 1$

Застосовується операція csort до матриць значень та мінтермальних ймовірностей для визначення розподілу для$X$.

Проілюструємо простим прикладом. Розширення на загальний випадок має бути досить кидатися в очі. Спочатку робимо завдання «від руки» в табличній формі. Потім використовуємо m-процедури для проведення потрібних операцій.

Приклад$\PageIndex{9}$ Finding the distribution from affine form

Будинок поштового замовлення містить три елементи (обмежте один з кожного виду на клієнта). Нехай

$E_1$= подія замовник замовляє пункт 1, за ціною 10 доларів.
$E_2$= подія замовник замовляє пункт 2, за ціною 18 доларів.
$E_3$= подія замовник замовляє пункт 3, за ціною 10 доларів.

Існує поштова плата в розмірі 3 доларів за замовлення.

Ми вважаємо$\{E_1, E_2, E_3\}$ незалежним з ймовірностями 0,6, 0,3, 0,5 відповідно. Дозвольте$X$ бути сума, яку клієнт, який замовляє спеціальні товари, витрачає на них плюс вартість розсилки. Потім, в афінній формі,

$X = 10 I_{E_1} + 18 I_{E_2} + 10 I_{E_3} + 3$

Ми шукаємо спочатку примітивну форму, використовуючи мінтермальні ймовірності, які можна обчислити в даному випадку за допомогою m-функції minprob.

Для отримання значення$X$ на кожному мінтермі ми

Помножте мінтермальний вектор для кожної породжуючої події на коефіцієнт для цієї події
Підсумуйте значення на кожному мінтермі і додайте константу

Щоб заповнити таблицю, перерахуйте відповідні мінтермальні ймовірності.

$i$	10$I_{E_1}$	18$I_{E_2}$	10$I_{E_3}$	c	$s-i$	$pm_i$
0	0	0	0	3	3	0,14
1	0	0	10	3	13	0,14
2	0	18	0	3	21	0,06
3	0	18	10	3	31	0,06
4	10	0	0	3	13	0,21
5	10	0	10	3	23	0,21
6	10	18	0	3	31	0,09
7	10	18	10	3	41	0,09

Потім ми сортуємо на$s_i$, значення на різних$M_i$, щоб викрити більш чітко примітивну форму для$X$.

Значення «Примітивна форма»
$i$	$s_i$	$pm_i$
0	3	0,14
1	13	0,14
4	13	0,21
2	21	0,06
5	23	0,21
3	31	0,06
6	31	0,09
7	41	0,09

Примітивна форма$X$ є таким чином

\ (X = 3I_ {М_0} + 12I_ {M_1} + 13I_ {M_4} + 21I_ {M_2} + 23I_ {M_5} + 31I_ {M_3} + 31I_ {M_6} + 41I_ {M_7}

Відзначимо, що значення 13 приймається на мінтермах$M_1$ і$M_4$. Імовірність$X$ має значення 13, таким чином$p(1) + p(4)$. Аналогічно$X$ має значення 31 на мінтермах$M_3$ і$M_6$.

Для завершення процесу визначення розподілу перерахуємо відсортовані значення і закріпимо, склавши воєдино ймовірності мінтермів, на яких береться кожне значення, наступним чином:

$k$	$t_k$	$p_k$
1	3	0,14
2	13	0.14 + 0,21 = 0,35
3	21	0,06
4	23	0,21
5	31	0.06 + 0.09 = 0,15
6	41	0,09

Результати можуть бути поміщені в матрицю$X$ можливих значень і відповідну матрицю PX ймовірностей, яка$X$ приймає кожне з цих значень. Експертиза таблиці показує, що

$X =$[3 13 21 23 31 41] і$PX =$ [0.14 0.35 0,06 0.21 0.15 0.09]

Матриці$X$ та PX описують розподіл для$X$.

M-процедура визначення розподілу від афінної форми

Зараз ми розглянемо відповідні етапи MATLAB у визначенні розподілу від афінної форми, а потім включимо їх у канонічну m-процедуру для здійснення трансформації. Ми починаємо з випадкової величини в афінній формі, і припустимо, що ми маємо доступні або можемо обчислити, мінтермальні ймовірності.

Процедура використовує mintable для встановлення основних векторних шаблонів minterm, потім використовує матрицю коефіцієнтів, включаючи постійний член (встановлений нулем, якщо відсутній), для отримання значень на кожному мінтермі. Мінтермальні ймовірності включені в матрицю рядків.
Отримавши значення на кожному мінтермі, процедура виконує потрібну консолідацію за допомогою m-функції csort.

Приклад$\PageIndex{10}$ Steps in determining the distribution for X in Example 6.1.9

>> c = [10 18 10 3];                 % Constant term is listed last
>> pm = minprob(0.1*[6 3 5]);
>> M  = mintable(3)                  % Minterm vector pattern
M =
     0     0     0     0     1     1     1     1
     0     0     1     1     0     0     1     1
     0     1     0     1     0     1     0     1
% - - - - - - - - - - - - - -        % An approach mimicking ``hand'' calculation
>> C = colcopy(c(1:3),8)             % Coefficients in position
C =
    10    10    10    10    10    10    10    10
    18    18    18    18    18    18    18    18
    10    10    10    10    10    10    10    10
>> CM = C.*M                         % Minterm vector values
CM =
     0     0     0     0    10    10    10    10
     0     0    18    18     0     0    18    18
     0    10     0    10     0    10     0    10
>> cM = sum(CM) + c(4)               % Values on minterms
cM =
     3    13    21    31    13    23    31    41
% - - - - - - - - - - - -  -         % Practical MATLAB procedure
>> s = c(1:3)*M + c(4)
s =
     3    13    21    31    13    23    31    41
>> pm = 0.14  0.14  0.06  0.06  0.21  0.21  0.09  0.09   % Extra zeros deleted
>> const = c(4)*ones(1,8);}

>> disp([CM;const;s;pm]')            % Display of primitive form
     0     0     0   3    3    0.14  % MATLAB gives four decimals
     0     0    10   3   13    0.14
     0    18     0   3   21    0.06
     0    18    10   3   31    0.06
    10     0     0   3   13    0.21
    10     0    10   3   23    0.21
    10    18     0   3   31    0.09
    10    18    10   3   41    0.09
>> [X,PX] = csort(s,pm);              % Sorting on s, consolidation of  pm
>> disp([X;PX]')                      % Display of final result
     3    0.14
    13    0.35
    21    0.06
    23    0.21
    31    0.15
    41    0.09

Два основних етапи об'єднані в m-процедуру canonic, яку ми використовуємо для вирішення попередньої проблеми.

Приклад$\PageIndex{11}$ Use of canonic on the variables of Example 6.1.10

>> c = [10 18 10 3]; % Note that the constant term 3 must be included last
>> pm = minprob([0.6 0.3 0.5]);
>> canonic
 Enter row vector of coefficients  c
 Enter row vector of minterm probabilities  pm
Use row matrices X and PX for calculations
Call for XDBN to view the distribution
>> disp(XDBN)
    3.0000    0.1400
   13.0000    0.3500
   21.0000    0.0600
   23.0000    0.2100
   31.0000    0.1500
   41.0000    0.0900

З розподілом, доступним у матрицях$X$ (набір значень) та PX (набір ймовірностей), ми можемо обчислити найрізноманітніші величини, пов'язані з випадковою величиною.

Ми використовуємо два ключових пристрої:

Використовуйте реляційні та логічні операції над матрицею значень,$X$ щоб визначити матрицю,$M$ яка має ті значення, які відповідають заданій умові. $P(X \in M)$: ПМ = М* РХ
Визначте$G = g(X) = [g(X_1) g(X_2) \cdot\cdot\cdot g(X_n)]$ за допомогою операцій масиву на матриці$X$. У нас є дві альтернативи:
1. Використовуйте матрицю$G$, яка має значення$g(t_i)$ для кожного можливого значення$t_i$ для$X$, або,
2. Застосуйте csort до пари$(G, PX)$, щоб отримати розподіл для$Z = g(X)$. Цей розподіл (у матрицях значень та ймовірностей) може бути використаний точно так само, як і для вихідної випадкової величини$X$.

Приклад$\PageIndex{12}$ Continuation of Example 6.1.11

Припустимо, для випадкової величини$X$ в прикладі 6.11 бажано визначити ймовірності

$P(15 \le X \le 35)$,$P(|X - 20| \le 7)$, і$(X - 10) (X - 25) > 0)$

>> M = (X>=15)&(X<=35);
M = 0   0    1    1    1    0    % Ones for minterms on which 15 <= X <= 35
>> PM = M*PX'                    % Picks out and sums those minterm probs
PM =  0.4200
>> N = abs(X-20)<=7;
N = 0    1    1    1    0    0   % Ones for minterms on which |X - 20| <= 7
>> PN = N*PX'                    % Picks out and sums those minterm probs
PN =  0.6200
>> G = (X - 10).*(X - 25)
G = 154 -36 -44 -26 126 496      % Value of g(t_i) for each possible value
>> P1 = (G>0)*PX'                % Total probability for those t_i such that
P1 =  0.3800                     % g(t_i) > 0
>> [Z,PZ] = csort(G,PX)          % Distribution for Z = g(X)
Z =  -44   -36   -26   126   154   496
PZ =  0.0600    0.3500    0.2100    0.1500    0.1400    0.0900
>> P2 = (Z>0)*PZ'                % Calculation using distribution for Z
P2 =  0.3800

Приклад$\PageIndex{13}$ Alternate formulation of Example 4.3.3 from "Composite Trials"

Десять гоночних автомобілів беруть участь у випробуваннях часу, щоб визначити полюсні позиції для майбутньої гонки. Щоб кваліфікуватися, вони повинні розмістити середню швидкість 125 миль/год або більше на пробному запуску. Нехай$E_i$ буде подією$i$ тй автомобіль робить кваліфікаційну швидкість. Здається розумним припустити,$\{E_i: 1 \le i \le 10\}$ що клас незалежний. Якщо відповідні ймовірності успіху становлять 0,90, 0,88, 0,93, 0,77, 0,85, 0,96, 0,72, 0,83, 0,91, 0,84, яка ймовірність того, що$k$ або більше буде кваліфікуватися ($k$= 6,7,8,9,10)?

Рішення

Нехай$X = \sum_{i = 1}^{10} I_{E_i}$

>> c = [ones(1,10) 0];
>> P = [0.90, 0.88, 0.93, 0.77, 0.85, 0.96, 0.72, 0.83, 0.91, 0.84];
>> canonic
 Enter row vector of coefficients  c
 Enter row vector of minterm probabilities  minprob(P)
Use row matrices X and PX for calculations
Call for XDBN to view the distribution
>> k = 6:10;
>> for i = 1:length(k)
    Pk(i) = (X>=k(i))*PX';
end
>> disp(Pk)
    0.9938    0.9628    0.8472    0.5756    0.2114

Таке рішення не так зручно виписувати. Однак з розподілом для$X$ як визначено, можна визначити безліч інших ймовірностей. Особливо це стосується випадків, коли бажано порівняти результати двох незалежних заїздів або «заїздів». Розглядаються такі проблеми при дослідженні незалежних класів випадкових величин.

Функціональна форма для канонічних

Одним з недоліків процедури canonic є те, що вона завжди називає вихід$X$ і PX. Хоча їх можна легко перейменувати, часто бажано використовувати якесь інше ім'я для випадкової величини з самого початку. Форма функції, яку ми називаємо canonicf, корисна в даному випадку.

Приклад$\PageIndex{14}$ Alternate solution of Example 6.1.13, using canonicf

>> c = [10 18 10 3];
>> pm = minprob(0.1*[6 3 5]);
>> [Z,PZ] = canonicf(c,pm);
>> disp([Z;PZ]')                % Numbers as before, but the distribution
    3.0000    0.1400            % matrices are now named Z and PZ
   13.0000    0.3500
   21.0000    0.0600
   23.0000    0.2100
   31.0000    0.1500
   41.0000    0.0900

Загальні випадкові величини

Розподіл для простої випадкової величини легко візуалізується у вигляді точкових масових концентрацій при різних значеннях в діапазоні, а клас подій, визначених простою випадковою величиною, описується в терміні розбиття, породженого$X$ (тобто класом тих подій виду $A_i = [X = t_i]$для кожного$t_i$ в асортименті). Ситуація концептуально та ж для загального випадку, але деталі складніше. Якщо випадкова величина приймає континуум значень, то розподіл маси ймовірності може бути плавно розподілений по лінії. Або розподіл може бути сумішшю точкових масових концентрацій і плавних розподілів на деяких інтервалах. Класом подій$X$ визначається множина всіх обернених зображень$X^{-1} (M)$ для$M$ будь-якого члена загального класу підмножин дійсного рядка, відомого в математичній літературі як множини Бореля. Існують технічні математичні причини не сказати, що M - це будь-яка підмножина, але клас множин Бореля є досить загальним, щоб включати будь-який набір, який може зустрічатися в додатках - звичайно, на рівні цього лікування. Набори Бореля включають будь-який інтервал і будь-який набір, який може бути сформований доповненнями, підрахунковими союзами та лічильними перетинами множин Бореля. Це тип класу, відомий як сигма-алгебра подій. Через збереження множини операцій зворотним зображенням клас подій, що визначаються випадковою величиною, також$X$ є сигма-алгеброю, і часто позначається$\sigma(X)$. Є деякі технічні питання щодо міри ймовірності$X$,$P_X$ викликаної, отже, розподіл. Вони також врегульовані таким чином, що немає необхідності в занепокоєнні на цьому рівні аналізу. Однак деякі з цих питань стають важливими при роботі з випадковими процесами та іншими просунутими поняттями, які все частіше використовуються в додатках. Два факти забезпечують свободу, яку нам потрібно продовжувати з невеликою турботою про технічні деталі.

$X^{-1} (M)$подія для кожного Borel set$M$ iff для кожного напівнескінченного інтервалу$(-\infty, t]$ на реальному рядку$X^{-1} ((-\infty, t])$ є подією.
Індукований розподіл ймовірностей визначається однозначно його присвоєнням всім інтервалам форми$(-\infty, t]$.

Ці факти вказують на важливість функції розподілу, введеної в наступному розділі.

Інший факт, згаданий вище і детально розглянутий в наступному розділі, полягає в тому, що будь-яка загальна випадкова величина може бути наближена так само близько, як задоволена простою випадковою величиною. У наступному розділі ми перейдемо до опису деяких поширених розподілів ймовірностей і способів їх опису аналітично.

\(c_j\)	2.00	1,50	2.00	2.50	1,50	1,50	1.00	2.50	2.00	1,50
\(P(C_j)\)	0,08	0,11	0,07	0,15	0,10	0,09	0,14	0,08	0,08	0,10

\(i\)	10\(I_{E_1}\)	18\(I_{E_2}\)	10\(I_{E_3}\)	c	\(s-i\)	\(pm_i\)
0	0	0	0	3	3	0,14
1	0	0	10	3	13	0,14
2	0	18	0	3	21	0,06
3	0	18	10	3	31	0,06
4	10	0	0	3	13	0,21
5	10	0	10	3	23	0,21
6	10	18	0	3	31	0,09
7	10	18	10	3	41	0,09

\(i\)	\(s_i\)	\(pm_i\)
0	3	0,14
1	13	0,14
4	13	0,21
2	21	0,06
5	23	0,21
3	31	0,06
6	31	0,09
7	41	0,09

\(k\)	\(t_k\)	\(p_k\)
1	3	0,14
2	13	0.14 + 0,21 = 0,35
3	21	0,06
4	23	0,21
5	31	0.06 + 0.09 = 0,15
6	41	0,09