2.1: Мінтермс

Перегородки і мінтерми

Щоб побачити, як природним чином виникає фундаментальна перегородка, розглянемо спочатку розділ основного простору, виробленого єдиною подією\(A\).

\[\Omega = A \bigvee A^c\]

Тепер якщо\(B\) це друга подія, то

\[A = AB \bigvee AB^c\]

і

\[A^c = A^c B \bigvee A^c B^c\]

так що

\[\Omega = A^c B^c \bigvee A^c B \bigvee AB^c \bigvee AB\]

Пара\(\{A, B\}\)\(\Omega\) розділилася на\(\{A^c B^c, A^c B, AB^c, AB\}\). Продовження саме таким чином призводить систематично до поділу на три події\(\{A, B, C\}\), чотири події\(\{A, B, C, D\}\) і т.д.

Ми ілюструємо фундаментальні закономірності у випадку чотирьох подій\(\{A, B, C, D\}\). Формуємо мінтерми як перетину членів класу, з різними закономірностями доповнення. Для класу з чотирьох подій існують\(2^4 = 16\) такі закономірності, звідси і 16 мінтермів. Це, в систематичній домовленості,

\(A^c B^c C^c D^c\)	\(A^c B C^c D^c\)	\(A B^c C^c D^c\)	\(A B C^c D^c\)
\(A^c B^c C^c D\)	\(A^c B C^c D\)	\(A B^c C^c D\)	\(A B C^c D\)
\(A^c B^c C D^c\)	\(A^c B C D^c\)	\(A B^c C D^c\)	\(A B C D^c\)
\(A^c B^c C D\)	\(A^c B C D\)	\(A B^c C D\)	\(A B C D\)

Жоден елемент не може бути більш ніж за один мінтермін, тому що кожен відрізняється від інших доповненням хоча б однієї події учасника. Кожному елементу\(\omega\) присвоюється рівно один з мінтермів шляхом визначення відповідей на чотири питання:

Це в\(A\)? Це в\(B\)? Це в\(C\)? Це в\(D\)?

Припустимо, наприклад, відповіді такі: Так, Ні, Ні, Так. Тоді ω знаходиться в мінтермі\(A B^c C^c D\). Аналогічним чином ми можемо визначити приналежність кожного\(\omega\) в базовому просторі. Таким чином, мінтерми утворюють перегородку. Тобто мінтерми являють собою взаємовиключні події, одне з яких обов'язково відбудеться на кожному судовому розгляді. Членство будь-якого мінтерму залежить від членства кожного генеруючого набору\(A, B, C\) або\(D\), і відносин між ними. Для деяких класів один або кілька мінтермів є порожніми (неможливі події). Як ми бачимо нижче, це не викликає ніяких проблем.

Експертиза розвитку вище показує, що якщо ми починаємо з класу n подій, існують\(2^n\) мінтерми. Щоб допомогти в систематичному поводженні, ми запроваджуємо просту систему нумерації для мінтермів, яку ми проілюструємо, знову розглядаючи чотири події\(A, B, C, D\), в такому порядку. Відповіді на чотири питання вище можна представити чисельно схемою

Ні\(\sim 0\) і так\(\sim 1\)

Таким чином, якщо\(\omega\) знаходиться в\(A^c B^c C^c D^c\), відповіді табличні як 0 0 0 0. Якщо\(\omega\) знаходиться в\(A B^c C^c D\), то це позначається 1 0 0 1. При такій схемі розташування мінтерма вище стає

0000\(\sim\) 0	0100\(\sim\) 4	1000\(\sim\) 8	1100\(\sim\) 12
0001\(\sim\) 1	0101\(\sim\) 5	1001\(\sim\) 9	1101\(\sim\) 13
0010\(\sim\) 2	0110\(\sim\) 6	1010\(\sim\) 10	1110\(\sim\) 14
0011\(\sim\) 3	0111\(\sim\) 7	1011\(\sim\) 11	1111\(\sim\) 15

Ми можемо розглядати ці четвірки нулів і одиниць як двійкові зображення цілих чисел, які також можуть бути представлені їх десятковими еквівалентами, як показано в таблиці. Часто корисно посилатися на мінтерми за номером. Якщо члени генеруючого класу обробляються у фіксованому порядку, то кожне число minterm, що надійшло у вищевказаному порядку, визначає minterm однозначно. Таким чином, для генеруючого класу\(\{A, B, C, D\}\), в такому порядку, ми можемо позначити

\(A^c B^c C^c D^c = M_0\)(мінтерм 0)\(AB^cC^c D = M_9\) (мінтерм 9) і т.д.

Ми використовуємо цю схему нумерації на спеціальних діаграмах Венна, які називаються minterm maps. Вони проілюстровані на малюнку, для випадків трьох, чотирьох та п'яти генеруючих подій. Оскільки фактичний зміст будь-якого мінтерма залежить від множин\(A, B, C\), а\(D\) в генеруючому класі прийнято називати ці множини змінними. У випадку з трьома змінними, set\(A\) є правою половиною діаграми, а set\(C\) - нижня половина; але набір B розділений, так що це об'єднання другого та четвертого стовпців. Подібні розколи трапляються і в інших випадках.

Зауваження. Інші корисні домовленості мінтерм-карт використовуються при аналізі схем комутації.

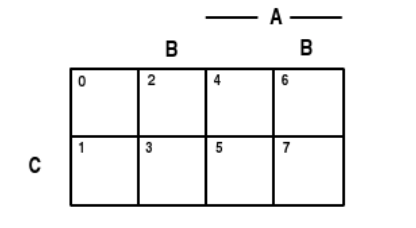
Три змінні

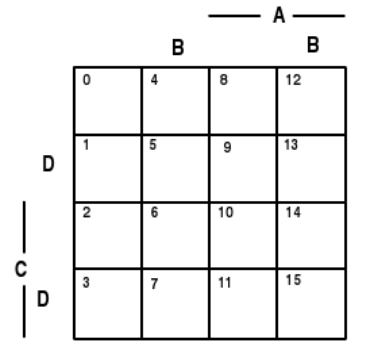
Чотири змінні

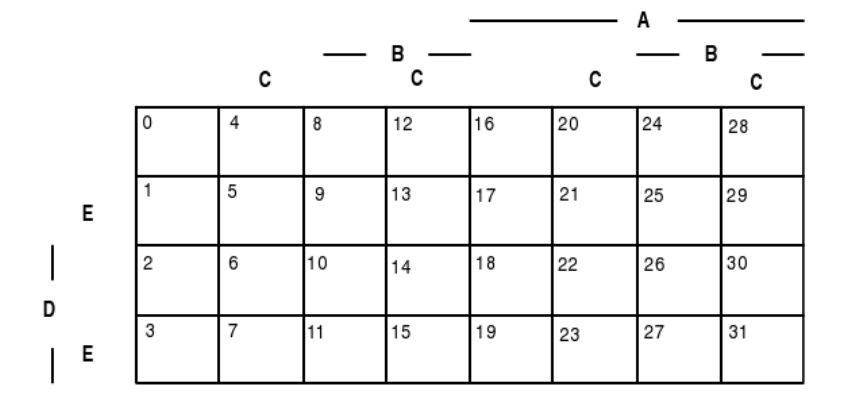
П'ять змінних

Малюнок 2.1.1. Мінтерм карти для трьох, чотирьох або п'яти змінних

Мінтерм карти і мінтерм розширення

Значення мінтермального поділу основного простору багато в чому спирається на наступний факт.

Мінтермінне розширення

Кожна логічна комбінація елементів у генеруючому класі може бути виражена як нероздільне об'єднання відповідного підкласу мінтермів. Це уявлення відоме як мінтермальне розширення для комбінації.

При отриманні виразу для заданої логічної комбінації, яка тримає для будь-якого класу\(\{A, B, C, D\}\) з чотирьох подій, ми включаємо всі можливі мінтерми, будь то порожній чи ні. Якщо minterm порожній для даного класу, його наявність не змінює вміст набору або присвоєння ймовірності для булевої комбінації.

Існування та унікальність розширення стає правдоподібним на простих прикладах з використанням мінтермальних карт для графічного визначення мінтермального змісту різних логічних комбінацій. Використовуючи систему розташування та нумерації, введену вище, ми дозволимо\(M_i\) представляти\(i\) той мінтерм (нумерація від нуля) і нехай\(p(i)\) представляємо ймовірність цього мінтерму. Коли ми маємо справу з об'єднанням мінтермів у мінтермальному розширенні, зручно використовувати скорочення, проілюстроване нижче.

\(M(1, 3, 7) = M_1 \bigvee M_3 \bigvee M_7\)і\(p(1, 3, 7) = p(1) + p(3) + p(7)\)

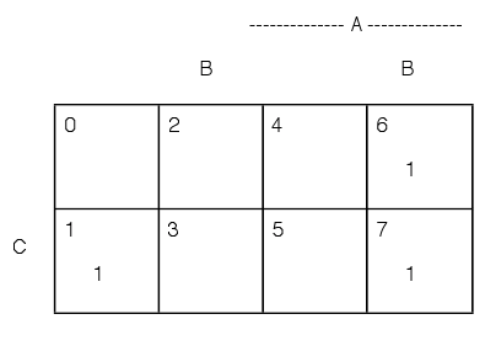
Малюнок 2.1.2. \(E = AB \cup A^c (B \cup C^c)^c = M(1:6, 7)\)Мінтерм-розширення для прикладу 2.1.1

Розглянемо наступний простий приклад.

Приклад\(\PageIndex{1}\) Minterm expansion

Припустимо\(E = AB \cup A^c (B \cup C^c)^c\). Експертиза мінтерм-карти на малюнку 2.1.2 показує, що\(AB\) складається з об'єднання\(M_6\) мінтермів\(M_7\), які ми позначимо\(M(6,7)\). Поєднання\(B \cup C^c = M(0, 2, 3, 4, 6, 7)\), так що його доповнюють\((B \cup C^c)^c = M(1, 5)\). Це залишає загальну частину\(A^c (B \cup C^c)^c = M_1\), отже,\(E = M(1, 6, 7)\). Аналогічно,\(F = A \cup B^c C = M(1, 4, 5, 6, 7)\).

Ключем до встановлення розширення є зауваження, що кожен мінтерм є або підмножиною комбінації, або не з'єднаний з нею. Розширення, таким чином, є об'єднанням тих мінтермів, включених в комбінацію. Загальна перевірка з використанням індикаторних функцій намальована в останньому розділі цього модуля.

Використання мінтерм карт

Типова задача шукає ймовірність певних булевих комбінацій класу подій, коли задано ймовірності різних інших комбінацій. Розглянемо кілька простих прикладів і проілюструємо використання мінтерм-карт у формулюванні та розв'язанні.

Приклад\(\PageIndex{2}\) Survey on software

Статистичні дані беруться для певного студентського населення з персональними комп'ютерами. Індивід вибирається випадковим чином. Нехай\(A =\) подія, яку вибрана особа має обробку\(B =\) текстів, подія, яку він або вона має програму розповсюдження аркушів, і\(C =\) подія, яку людина має програму бази даних. Дані мають на увазі

• Імовірність дорівнює 0.80, що у людини є програма для обробки текстів:\(P(A) = 0.8\)
• Імовірність становить 0,65, що у людини є програма розвороту листів:\(P(B) = 0.65\)
• Ймовірність 0,30, що у людини є програма бази даних:\(P(C) = 0.3\)
• Імовірність дорівнює 0,10, що у людини є всі три:\(P(ABC) = 0.1\)
• Імовірність 0,05, що людина не має ні обробки текстів, ні розкладного листа:\(P(A^c B^c = 0.05\)
• Імовірність становить 0,65, що у людини є як мінімум два:\(P(AB \cup AC \cup BC) = 0.65\)
• Імовірність текстового процесора і бази даних, але без розвороту аркуша вдвічі більша ймовірність поширення аркуша і бази даних, але немає\(P(AB^cC) = 2P(A^cBC)\)
  
  текстового процесора: а Яка ймовірність того, що людина має рівно дві програми?
  б Яка ймовірність того, що людина має тільки програму бази даних?

Виникає кілька питань:

• Чи є ці дані узгодженими?
• Чи достатньо даних, щоб відповісти на питання?
• Як дані можуть бути використані для відповіді на питання?

Рішення

Дані, виражені з точки зору мінтермінних ймовірностей, такі:

\(P(A) = p(4, 5, 6, 7) = 0.80\); звідси\(P(A^c) = p(0, 1, 2, 3) = 0.20\)

\(P(B) = p(2, 3, 6, 7) = 0.65\); звідси\(P(B^c) = p(0, 1, 4, 5) = 0.35\)

\(P(C) = p(1, 3, 5, 7) = 0.30\); звідси\(P(C^c) = p(0, 2, 4, 6) = 0.70\)

\(P(ABC) = p(7) = 0.10\)\(P(A^c B^c) = p(0, 1) = 0.05\)

\(P(AB \cup AC \cup BC) = p(3, 5, 6, 7) = 0.65\)

\(P(AB^c C) = p(5) = 2p(3) = 2P(A^c BC)\)

Ці дані наведені на карті minterm на малюнку 2.1.3 a Ми використовуємо шаблони, відображені на карті minterm, щоб допомогти в алгебраїчному розв'язанні для різних мінтермальних ймовірностей.

\(p(2, 3) = p(0, 1, 2, 3) - p(0, 1) = 0.20 - 0.05 = 0.15\)

\(p(6,7) = p(2, 3, 6, 7) - p(2, 3) = 0.65 - 0.15 = 0.50\)

\(p(6) = p(6,7) - p(7) = 0.50 - 0.10 = 0.40\)

\(p(3,5) = p(3, 5, 6, 7) - p(6,7) = 0.65 -0.50 = 0.15 \Rightarrow p(3) = 0.05\),

\(p(5) = 0.10 \Rightarrow p(2) = 0.10\)

\(p(1) = p(1, 3, 5, 7) - p(3, 5) - p(7) = 0.30 - 0.15 - 0.10 = 0.05 \Rightarrow p(0) = 0\)

\(p(4) = p(4, 5, 6, 7) - p(5) - p(6, 7) = 0.80 - 0.10 - 0.50 = 0.20\)

Таким чином, визначаються всі проміжні ймовірності. Вони відображаються на малюнку 2.1.3 б. з них отримуємо

\(P(A^c BC \bigvee AB^cC \bigvee ABC^c) = p(3, 5, 6) = 0.05 + 0.10 + 0.40 = 0.55\)і\(P(A^c B^c C) = p(1) = 0.05\)

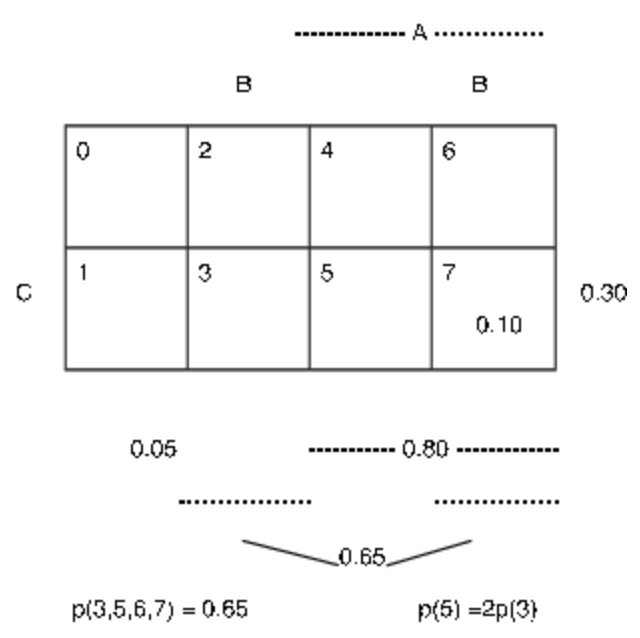
a. дані для обстеження програмного забезпечення, приклад 2.3.1

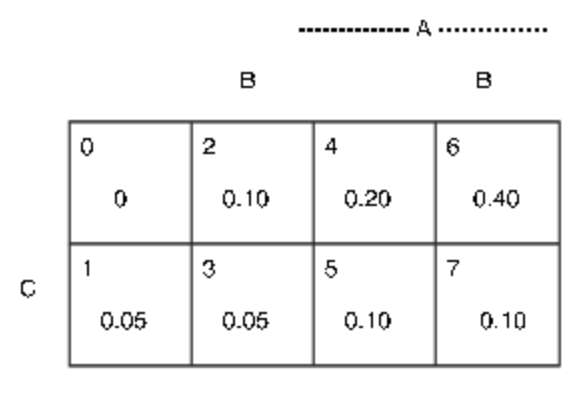
b Мінтермальні ймовірності для обстеження програмного забезпечення. Приклад 3.3.1

Малюнок 2.1.3. Мінтерм карти для обстеження програмного забезпечення.

Приклад\(\PageIndex{3}\) Survey on personal computers

Опитування 1000 студентів показує, що 565 мають настільні комп'ютери, сумісні з ПК, 515 мають настільні комп'ютери Macintosh, а 151 мають портативні комп'ютери. 51 мають всі три, 124 мають як ПК, так і портативні комп'ютери, 212 мають принаймні два з трьох, і вдвічі більше володіють як ПК, так і ноутбук, як ті, хто має обидва Настільний комп'ютер Macintosh і ноутбук. Людина вибирається навмання з цієї популяції. Яка ймовірність того, що він чи вона має хоча б один з цих типів комп'ютерів? Яка ймовірність того, що у обраної людини є тільки ноутбук?

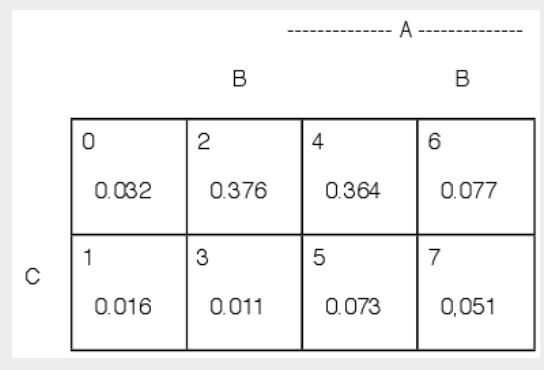
Малюнок 2.1.4. Мінтермінні ймовірності для комп'ютерного опитування. Приклад 2.1.3

Рішення

Нехай\(A =\) подія володіння настільним ПК,\(B =\) подія володіння настільним комп'ютером Macintosh та\(C =\) подія володіння ноутбуком. Ми використовуємо карту minterm для трьох змінних, щоб допомогти визначити minterm закономірності. Наприклад, захід\(AC = M_5 \bigvee M_7\) так, що\(P(AC) = p(5) + p(7) = p(5, 7)\).

Дані, виражені з точки зору мінтермінних ймовірностей, такі:

\(P(A) = p(4, 5, 6, 7) = 0.565\), звідси\(P(A^c) = p(0, 1, 2, 3) = 0.435\)

\(P(B) = p(2, 3, 6, 7) = 0.515\), звідси\(P(B^c) = p(0, 1, 4, 5) = 0.485\)

\(P(C) = p(1, 3, 5, 7) = 0.151\), звідси\(P(C^c) = p(0, 2, 4, 6) = 0.849\)

\(P(ABC) = p(7) = 0.051\)\(P(AC) = p(5, 7) = 0.124\)

\(P(AB \cup AC \cup BC) = p(3, 5, 6, 7) = 0.212\)

\(P(AC) = p(5, 7) = 2p(3, 7) = 2 P(BC)\)

Ми використовуємо шаблони, відображені на карті minterm, щоб допомогти в алгебраїчному розв'язанні для різних мінтермальних ймовірностей.

\(p(5) = p(5, 7) - p(7) = 0.124 - 0.051 = 0.073\)

\(p(1, 3) = P(A^c C) = 0.151 - 0.124 = 0.027\)\(P(AC^c) = p(4, 6) = 0.565 - 0.124 = 0.441\)

\(p(3, 7) = P(BC) = 0.124/2 = 0.062\)

\(p(3) = 0.062 - 0.051 = 0.011\)

\(p(6) = p(3, 4, 6, 7) - p(3) - p(5, 7) = 0.212 - 0.011 - 0.124 = 0.077\)

\(p(4) = P(A) - p(6) - p(5, 7) = 0.565 - 0.077 - 0.1124 = 0.364\)

\(p(1) = p(1, 3) - p(3) = 0.027 - 0.11 = 0.016\)

\(p(2) = P(B) - p(3, 7) - p(6) = 0.515 - 0.062 - 0.077 = 0.376\)

\(p(0) = P(C^c) - p(4, 6) - p(2) = 0.849 0.441 - 0.376 = 0.032\)

Визначили мінтермальні ймовірності, які відображаються на мінтермальній карті Рисунок 2.1.4. Тепер ми можемо обчислити ймовірність будь-якої логічної комбінації генеруючих подій\(A, B, C\). Таким чином,

\(P(A \cup B \cup C) = 1 - P(A^c B^c C^c) - 1 - p(0) = 0.968\)і\(P(A^c B^c C) = p(1) = 0.016\)

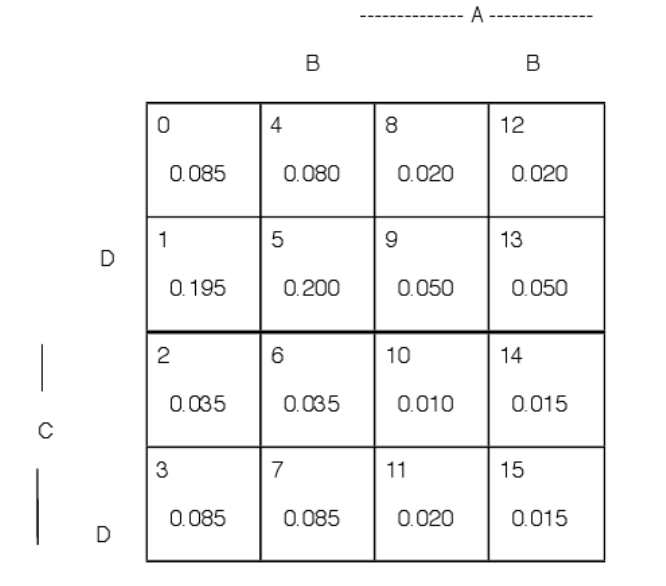
Малюнок 2.1.5. Мінтермінні ймовірності для опитування думок. Приклад 2.1.4

Приклад\(\PageIndex{4}\) Opinion survey

Проводиться опитування 1000 осіб для визначення їхньої думки щодо чотирьох пропозицій. \(A, B, C, D\)Дозволяти подіям обраної особи погоджується з відповідними пропозиціями. Результати опитування показують наступні ймовірності для різних комбінацій:

\(P(A) = 0.200\),\(P(B) = 0.500\),\(P(C) = 0.300\),\(P(D) = 0.700\),\(P(A(B \cup C^c) D^c) = 0.055\)

\(P(A \cup BC \cup D^c) = 0.520\),\(P(A^cBC^c D) = 0.120\),\(P(ABCD) = 0.015\),\(P(AB^c C) = 0.030\)

\(P(A^c B^c C^c D) = 0.195\),\(P(A^c BC) = 0.120\),\(P(A^c B^c D^c) = 0.120\),\(P(AC^c) = 0.140\)

\(P(ACD^c) = 0.025\),\(P(ABC^cD^c) = 0.020\)

Визначте ймовірності для кожного мінтерму і для кожної з наступних комбінацій:

\(A^c (BC^c \cup B^c C)\)- тобто не\(A\) і (\(B\)або\(C\), але не обидва)

\(A \cup BC^c\)- тобто,\(A\) або (\(B\)і ні\(C\))

Рішення

На початку не зрозуміло, чи дані є послідовними або достатніми для визначення мінімальних ймовірностей. Однак експертиза даних показує, що існує шістнадцять пунктів (включаючи той факт, що сума всіх мінтермальних ймовірностей одна). Таким чином, є надія, але немає впевненості в тому, що рішення існує. Поетапна процедура ліквідації, як і в попередніх прикладах, показує, що всі мінтерми насправді можуть бути розраховані. Результати відображаються на мінтерм-карті на малюнку 2.1.5. Хочеться вміти систематично аналізувати проблему. Формулювання вище передбачає більш систематичну алгебраїчну рецептуру, яка повинна зробити можливим автоматичне рішення.

Систематична рецептура

Використання мінтермальної карти має перевагу візуалізації мінтермального розширення в прямому відношенні до логічної комбінації. Алгебраїчні розв'язки попередніх задач передбачали спеціальні маніпуляції з даними мінтермальних комбінацій ймовірностей для пошуку ймовірності бажаної цільової комбінації. Ми шукаємо систематичне формулювання даних у вигляді набору лінійних алгебраїчних рівнянь з мінтермальними ймовірностями як невідомими, щоб можна було використовувати стандартні методи розв'язання. Розглянемо ще раз опитування програмного забезпечення Приклад 2.1.1.

Приклад\(\PageIndex{5}\) The softerware survey problem reformulated

Дані, виражені з точки зору мінтермінних ймовірностей, такі:

\(P(A) = p(4, 5, 6, 7) = 0.80\)

\(P(B) = p(2, 3, 6, 7) = 0.65\)

\(P(C) = p(1, 3, 5, 7) = 0.30\)

\(P(ABC) = p(7) = 0.10\)

\(P(A^cB^c) = p(0,1) = 0.05\)

\(P(AB \cup AC \cup BC) = p(3, 5, 6, 7) = 0.65\)

\(P(AB^cC) = p(5) = 2p(3) = 2P(A^cBC)\), щоб\(p(5) - 2p(3) = 0\)

У нас також є в будь-якому випадку

\(P(\Omega) = P(A \cup A^c) = p(0,1, 2, 3, 4, 5, 6, 7) = 1\)

завершити вісім пунктів даних, необхідних для визначення всіх восьми мінтермальних ймовірностей. Перша база може бути виражена у вигляді рівняння в мінтермових ймовірностях:

\(0 \cdot p(0) + 0 \cdot p(1) + 0 \cdot p(2) + 0 \cdot p(3) + 1 \cdot p(4) + 1 \cdot p(5) + 1 \cdot p(6) + 1 \cdot p(7) = 0.80\)

Це алгебраїчне рівняння в\(p(0), \cdot\cdot\cdot, p(7)\) з матрицею коефіцієнтів

[0 0 0 1 1 1]

Інші можуть бути виписані відповідно, даючи вісім лінійних алгебраїчних рівнянь у восьми змінних\(p(0)\) через\(p(7)\). Кожне рівняння має матрицю або вектор коефіцієнтів нуль-один, що вказують, які мінтерми включені. Вони можуть бути записані в матричному вигляді наступним чином:

\(\begin{bmatrix} 1 & 1 & 1&  & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 &  & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 &  & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 &  & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 &  & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 &  & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 &  & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 &  & -2 & 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} p(0) \\ p(1) \\ p(2) \\ p(3) \\ p(4) \\ p(5) \\ p(6) \\ p(7) \end{bmatrix} = \begin{bmatrix} 1 \\ 0.80 \\ 0.65 \\ 0.30 \\ 0.10 \\0.05 \\ 0.65 \\ 0 \end{bmatrix} = \begin{bmatrix} P(\Omega) \\ P(A) \\ P(B) \\ P(C) \\ P(ABC) \\ P(A^c B^c) \\ P(AB \cup AC \cup BC) \\ P(AB^cC) - 2P(A^c BC) \end{bmatrix}\)

• Патерни в матриці коефіцієнтів визначаються логічними операціями. Ми отримали їх за допомогою мінтерм-карти.
• Рішення використовує алгебраїчну процедуру, яка може здійснюватися різними способами, включаючи кілька стандартних комп'ютерних пакетів для матричних операцій.

Ми показуємо в модулі Minterm Vectors і MATLAB, як ми можемо використовувати MATLAB для обох аспектів.

Функції індикатора і мінтермінне розширення

Попереднє обговорення індикаторної функції показує, що індикаторна функція для булевої комбінації множин є числовою значеною функцією індикаторних функцій для окремих множин.

• Як індикаторна функція приймає тільки значення нуль і одиниця.
• Значення індикаторної функції для будь-якої булевої комбінації має бути постійним на кожному мінтермі. Наприклад, для кожного ω в мінтермі\(AB^cCD^c\) ми повинні мати\(I_A(\omega) = 1\),\(I_B(\omega) = 0\),\(I_C(\omega) = 1\), і\(I_D(\omega) = 0\). Таким чином, будь-яка функція\(I_A\),\(I_B\),\(I_C\),\(I_D\) повинна бути постійною протягом мінтерму.
• Розглянемо булеву\(E\) комбінацію генеруючих установок. Якщо\(\omega\) є в\(E \cap M_i\), то\(I_E(\omega) = 1\) для всіх\(\omega \in M_i\), так що\(M_i \subset E\). Оскільки кожен\(\omega \in M_i\) або деякі\(i, E\) повинні бути об'єднанням тих мінтермів, які діляться\(\omega\) з\(E\).
• \(\{M_i: i \in J_E\}\)Дозволяти підклас тих мінтермів, на яких\(I_E\) має значення одиницю. Тоді

\(E = \bigvee_{J_E} M_i\)

який є мінімальним розширенням\(E\).