Площа прямокутника

Last updated
Save as PDF

Page ID: 97286

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Результати навчання

Знайдіть площу прямокутника.
Знайдіть висоту прямокутника, враховуючи, що площа дорівнює 1.

Прямокутники мають принципове значення в частині статистики, яка передбачає рівномірний розподіл. Кожен прямокутник має підставу, висоту та площу. Формула для площі прямокутника така:

\[\text{Area} = \text{Base} \times \text{Height} \label{AreaFormula} \]

При роботі з рівномірним розподілом площа представляє ймовірність того, що подія знаходиться в межах підстави.

Приклад\(\PageIndex{1}\)

Розглянемо прямокутник, показаний нижче.

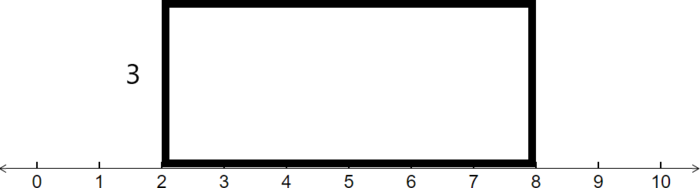
Прямокутник з основою від 2 до 8 і висотою 3.

Знайдіть площу цього прямокутника.

Рішення

Використовуємо формулу Площа (Equation\ ref {AreaFormula}). Щоб знайти базу, помічаємо, що вона проходить від 2 до 8, тому віднімаємо ці числа, щоб отримати базу:

\[Base\:=\:8\:-\:2\:=\:6\nonumber \]

Далі множимо на висоту, 3, щоб отримати

\[Area\:=\:Base\:\times Height\:=\:6\:\times3\:=\:18\nonumber \]

Приклад\(\PageIndex{2}\)

Виходить, що площа прямокутників, яка дорівнює 1, буде зустрічатися найчастіше для рівномірного розподілу. Припустимо, що ми знаємо, що площа прямокутника, який зображує рівномірний розподіл, дорівнює 1 і що основа прямокутника йде від 4 до 7. Знайдіть висоту прямокутника.

Рішення

Спочатку намалюйте прямокутник нижче, позначивши висоту як\(h\).

Прямокутник з основою від 4 до 7 і висотою h

Далі знайдіть основу прямокутника, що йде від 4 до 7 шляхом віднімання:

\[Base\:=\:7-4=3\nonumber \]

Далі підключіть те, що ми знаємо, до рівняння площі:

\[1\:=\:Area\:=\:Base\:\times Height\:=\:3\times h\nonumber \]

Це говорить нам про те, що 3 рази число дорівнює 1. Щоб дізнатися, що таке число, просто ділимо обидві сторони на 3, щоб отримати:

\[h=\frac{1}{3}\nonumber \]

Тому висота прямокутника площі 1 з основою від 4 до 7 дорівнює\(\frac{1}{3}\).

Приклад\(\PageIndex{3}\)

Припустимо, що ми знаємо, що площа прямокутника, який зображує рівномірний розподіл, дорівнює 1 і що основа прямокутника йде від 3 до 5. Існує менший прямокутник всередині більшого з тією ж висотою, але основа якого йде від 3,7 до 4,4. Знайдіть площу меншого прямокутника.

Рішення

Спочатку намалюйте більший прямокутник із заштрихованим меншим прямокутником.

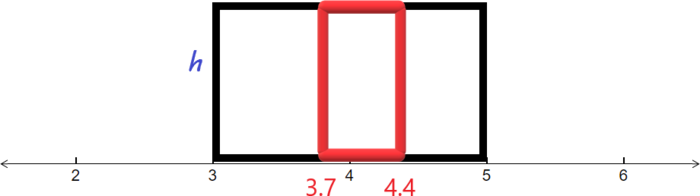
Невеликий прямокутник з основою від 3,7 до 4,4 в межах великого прямокутника з основою від 3 до 5

Далі знаходимо висоту прямокутника. Ми знаємо, що площа більшого прямокутника дорівнює 1. База йде від 3 до 5, тому база\(5-3=2\) Отже:

\[1\:=\:Area\:=\:Base\:\times Height\:=\:2h\nonumber \]

Діливши на 2, дає нам, що висота дорівнює\(\frac{1}{2}\) або 0,5. Тепер ми готові знайти площу меншого прямокутника. Спочатку знаходимо базу, віднімаючи:

\[\text{Base}\:=\:4.4-3.7\:=\:0.7\nonumber \]

Далі скористайтеся формулою площі:

\[Area\:=\:Base\:\times Height\:=\:0.7\:\times0.5\:=\:0.35\nonumber \]

Вправа\(\PageIndex{1}\)

Припустимо, що молодший вік учнів рівномірно розподілений від 5 до 11 років. Прямокутник, який зображує це, має основу від 5 до 11 і область 1. Прямокутник, який відображає ймовірність того, що випадково виділена дитина буде віком від 6,5 до 8,6 років, має основу від 6,5 до 8,6 і таку ж висоту, як і більший прямокутник. Знайдіть площу меншого прямокутника