11.7: Тест однієї дисперсії

Тест однієї дисперсії передбачає, що основний розподіл є нормальним. Нульова та альтернативна гіпотези викладені з точки зору дисперсії популяції (або стандартного відхилення населення). Статистика тесту така:

$$\chi^{2} = \frac{(n-1)s^{2}}{\sigma^{2}} \label{test}$$

де:

• $n$це загальна кількість даних
• $s^{2}$є дисперсією вибірки
• $\sigma^{2}$це дисперсія населення

Ви можете думати про$s$ випадкову величину в цьому тесті. Кількість ступенів свободи - це$df = n - 1$. Тест однієї дисперсії може бути правохвостий, лівохвостий або двохвостий. Наступний приклад покаже вам, як налаштувати нульову та альтернативну гіпотези. Нульова та альтернативна гіпотези містять твердження про дисперсію популяції.

Приклад$\PageIndex{1}$

Інструктори з математики зацікавлені не тільки в тому, як їхні студенти роблять на іспитах, в середньому, але як бали іспиту варіюються. Для багатьох інструкторів дисперсія (або стандартне відхилення) може бути важливішою, ніж середня.

Припустимо, інструктор з математики вважає, що стандартне відхилення для його підсумкового іспиту становить п'ять балів. Один з його кращих учнів думає інакше. Студент стверджує, що стандартне відхилення становить більше п'яти балів. Якби студент проводив тест гіпотези, якими були б нульові та альтернативні гіпотези?

Відповідь

Незважаючи на те, що нам дано стандартне відхилення населення, ми можемо налаштувати тест, використовуючи дисперсію населення наступним чином.

• $H_{0}: \sigma^{2} = 5^{2}$
• $H_{a}: \sigma^{2} > 5^{2}$

Вправа$\PageIndex{1}$

Інструктор SCUBA хоче записати колективні глибини кожного зі своїх учнів під час їх перевірки. Його цікавить, як змінюються глибини, хоча всі повинні були бути на одній глибині. Він вважає, що стандартне відхилення становить три фути. Його помічник вважає, що стандартне відхилення становить менше трьох футів. Якби інструктор проводив тест, якими були б нульові та альтернативні гіпотези?

Відповідь

• $H_{0}: \sigma^{2} = 3^{2}$
• $H_{a}: \sigma^{2} > 3^{2}$

Приклад$\PageIndex{2}$

З окремими лініями біля різних вікон поштове відділення виявляє, що стандартне відхилення для нормально розподіленого часу очікування для клієнтів у п'ятницю вдень становить 7,2 хвилини. Поштове відділення експериментує з єдиною, основною лінією очікування і виявляє, що для випадкової вибірки з 25 клієнтів час очікування клієнтів має стандартне відхилення 3,5 хвилини.

З рівнем значущості 5%, перевірити твердження, що один рядок викликає меншу різницю між часом очікування (коротший час очікування) для клієнтів.

Відповідь

Оскільки твердження полягає в тому, що один рядок викликає меншу варіацію, це тест однієї дисперсії. Параметр - дисперсія популяції$\sigma^{2}$, або стандартне відхилення популяції,$\sigma$.

Випадкова величина: стандартне відхилення$s$ зразка - це випадкова величина. Нехай$s = \text{standard deviation for the waiting times}$.

• $H_{0}: \sigma^{2} = 7.2^{2}$
• $H_{a}: \sigma^{2} < 7.2^{2}$

Слово «менше» говорить вам, що це тест з лівим хвостом.

Дистрибутив для тесту:$\chi^{2}_{24}$, де:

• $n = \text{the number of customers sampled}$
• $df = n - 1 = 25 - 1 = 24$

Обчисліть статистику тесту (Equation\ ref {test}):

$$\chi^{2} = \frac{(n-1)s^{2}}{\sigma^{2}} = \frac{(25-1)(3.5)^{2}}{7.2^{2}} = 5.67 \nonumber$$

де$n = 25$,$s = 3.5$, і$\sigma = 7.2$.

Графік:

Малюнок$\PageIndex{1}$.

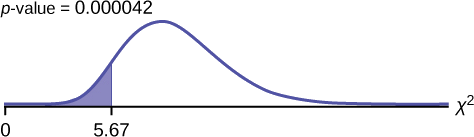
Заява про ймовірність:$p\text{-value} = P(\chi^{2} < 5.67) = 0.000042$

Порівняйте$\alpha$ і$p\text{-value}$:

$$\alpha = 0.05 (p\text{-value} = 0.000042 \alpha > p\text{-value} \nonumber$$

Прийміть рішення: З тих пір$\alpha > p\text{-value}$, відхилити$H_{0}$. Це означає, що ви відкидаєте$\sigma^{2} = 7.2^{2}$. Іншими словами, ви не думаєте, що зміна часу очікування становить 7,2 хвилини; ви думаєте, що зміна часу очікування менше.

Висновок: На рівні 5% значущості, з даних, є достатньо доказів, щоб зробити висновок, що один рядок викликає меншу різницю між часом очікування або з одним рядком час очікування клієнта змінюється менше 7,2 хвилин.

У 2-му DISR використовуйте 7: ρ2cdf. Синтаксис (нижній, верхній, df) для списку параметрів. Наприклад, 2cdf (-1Е99,5.67,24). The$p\text{-value} = 0.000042$.

Вправа$\PageIndex{2}$

FCC проводить тести швидкості широкосмугового зв'язку, щоб виміряти, скільки даних в секунду проходить між комп'ютером споживача та Інтернетом. Станом на серпень 2012 року стандартне відхилення швидкості Інтернету між провайдерами Інтернет-послуг (провайдерами) становило 12,2 відсотка. Припустимо, береться вибірка з 15 провайдерів, а стандартне відхилення - 13,2. Аналітик стверджує, що стандартне відхилення швидкостей більше, ніж повідомлялося. Викладіть нульову та альтернативну гіпотези, обчислите ступені свободи, статистику тесту, накидайте графік p -значення та зробіть висновок. Тест на рівні 1% значущості.

Відповідь

• $H_{0}: \sigma^{2} = 12.2^{2}$
• $H_{a}: \sigma^{2} > 12.2^{2}$

У 2-му DISTR використовуйте 7: 2cdf. Синтаксис (нижній, верхній, df) для списку параметрів. ρ2cd (16,39,10^99,14). The$p\text{-value} = 0.2902$.

$df = 14$

$$\text{chi}^{2} \text{test statistic} = 16.39 \nonumber$$

Малюнок$\PageIndex{2}$.

$p\text{-value}$Тобто$0.2902$, тому ми відмовляємося відкидати нульову гіпотезу. Недостатньо доказів, щоб припустити, що дисперсія більша, ніж$12.2^{2}$.

Посилання

1. «Посібники з цін Apple Insider». Інсайдер Apple, 2013. Доступно в Інтернеті за адресою http://appleinsider.com/mac_price_guide (доступ до 14 травня 2013 р.).
2. Дані Світового банку від 5 червня 2012 року.

Рецензія

Для перевірки мінливості використовуйте тест хі-квадрата однієї дисперсії. Тест може бути ліво-, правий або двохвіст, і його гіпотези завжди виражаються в терміні дисперсії (або стандартного відхилення).

Огляд формули

$\chi^{2} = \frac{(n-1) \cdot s^{2}}{\sigma^{2}}$Тест однієї дисперсійної статистики, де:

$n: \text{sample size}$

$s: \text{sample standard deviation}$

$\sigma: \text{population standard deviation}$

$df = n – 1 \text{Degrees of freedom}$

Тест однієї дисперсії

• Використовуйте тест, щоб визначити варіацію.
• Ступінь свободи - це$\text{number of samples} - 1$.
• Статистика тесту - це$\frac{(n-1) \cdot s^{2}}{\sigma^{2}}$, де$n = \text{the total number of data}$$s^{2} = \text{sample variance}$, і$\sigma^{2} = \text{population variance}$.
• Тест може бути ліво-, правий або двохвостий.

Використовуйте наступну інформацію, щоб відповісти на наступні три вправи: Стандартне відхилення лучника для його ударів - шість (дані вимірюються на відстані від центру цілі). Спостерігач стверджує, що стандартне відхилення менше.

Вправа$\PageIndex{3}$

Який тип тесту слід використовувати?

Відповідь

тест однієї дисперсії

Вправа$\PageIndex{4}$

Створіть нульову та альтернативну гіпотези.

Вправа$\PageIndex{5}$

Це правий, лівохвостий або двохвостий тест?

Відповідь

тест з лівого хвоста

Використовуйте наступну інформацію, щоб відповісти на наступні три вправи: Стандартне відхилення висот для учнів у школі становить 0,81. Береться випадкова вибірка з 50 учнів, а стандартне відхилення висот вибірки дорівнює 0,96. Дослідник, відповідальний за дослідження, вважає, що стандартне відхилення висот для школи перевищує 0,81.

Вправа$\PageIndex{6}$

Який тип тесту слід використовувати?

Вправа$\PageIndex{5}$

Створіть нульову та альтернативну гіпотези.

Відповідь

$H_{0}: \sigma^{2} = 0.81^{2}$;

$H_{a}: \sigma^{2} > 0.81^{2}$

Вправа$\PageIndex{6}$

$df =$________

Використовуйте наступну інформацію, щоб відповісти на наступні чотири вправи: Середній час очікування в кабінеті лікаря варіюється. Стандартне відхилення часу очікування в кабінеті лікаря становить 3,4 хвилини. Вибірка з 30 пацієнтів в кабінеті лікаря має стандартне відхилення часу очікування 4,1 хвилини. Один лікар вважає, що дисперсія часу очікування більша, ніж спочатку вважалося.

Вправа$\PageIndex{7}$

Який тип тесту слід використовувати?

Відповідь

тест однієї дисперсії

Вправа$\PageIndex{8}$

Що таке тестова статистика?

Вправа$\PageIndex{9}$

Що таке$p\text{-value}$?

Відповідь

0.0542

Вправа$\PageIndex{10}$

Що ви можете зробити висновок на рівні 5% значущості?