4.4: Біноміальний розподіл

Біноміальний розподіл часто використовується для моделювання кількості успіхів у вибірці розміру,$n$ проведеної із заміною чисельності населення$N$.

Три характеристики біноміального експерименту

1. Існує фіксована кількість випробувань. Подумайте про випробування як про повторення експерименту. Буква$n$ позначає кількість випробувань.
2. Є тільки два можливі результати, звані «успіх» і «невдача», для кожного судового розгляду. Буква$p$ позначає ймовірність успіху на одному випробуванні, і$q$ позначає ймовірність невдачі на одному випробуванні. $p + q = 1$.
3. $n$Випробування незалежні і повторюються з використанням однакових умов. Оскільки$n$ судові процеси незалежні, результат одного судового розгляду не допомагає передбачити результат іншого судового розгляду. Інший спосіб сказати це полягає в тому, що для кожного окремого випробування ймовірність успіху та ймовірності невдачі залишається однаковою.$p$$q$ Наприклад, випадкове вгадування на правдиво-помилкове статистичне запитання має лише два результати. Якщо на успіх ворожіння правильно, то невдача ворожить неправильно. Припустимо, Джо завжди правильно вгадає на будь-яку статистику істинно-помилкове питання з ймовірністю$p = 0.6$. Потім,$q = 0.4$. Це означає, що на кожне правдиво-помилкове статистичне запитання Джо відповідає, його ймовірність успіху ($p = 0.6$) та його ймовірність невдачі ($q = 0.4$) залишаються однаковими.

Результати біноміального експерименту відповідають біноміальному розподілу ймовірностей. Випадкова$X =$ величина - кількість успіхів, отриманих в$n$ незалежних випробуваннях. Середнє$\mu$ значення та дисперсія для$\sigma^{2}$ біноміального розподілу ймовірностей є

$$\mu = np$$

і

$$\sigma^{2} = npq.$$

Стандартне відхилення$\sigma$,

$$\sigma = \sqrt{npq}.$$

Будь-який експеримент, який має характеристики два і три і де$n = 1$ називається Судом Бернуллі (названий на честь Якова Бернуллі, який наприкінці 1600-х років їх широко вивчав). Біноміальний експеримент відбувається, коли кількість успіхів підраховується в одному або декількох випробуваннях Бернуллі.

Приклад$\PageIndex{1}$

У коледжі ABC коефіцієнт виведення з елементарного курсу фізики становить 30% для будь-якого даного терміну. Це означає, що протягом будь-якого даного терміну 70% учнів залишаються в класі протягом усього терміну. «Успіх» можна визначити як особа, яка вийшла. Випадкова$X =$ величина - кількість учнів, які вийшли з випадково обраного класу елементарної фізики.

Вправа$\PageIndex{1}$

Державна рада охорони здоров'я стурбована кількістю фруктів, доступних у шкільних обідах. Сорок вісім відсотків шкіл штату пропонують фрукти в обідах щодня. Це означає, що 52% цього не роблять. Яким був би «успіх» в цьому випадку?

Відповідь

школа, яка пропонує фрукти в їх обід кожен день

Приклад$\PageIndex{2}$

Припустимо, ви граєте в гру, яку ви можете тільки або виграти, або програти. Імовірність того, що ви виграєте будь-яку гру, становить 55%, а ймовірність того, що ви програєте - 45%. Кожна гра, в яку ви граєте, незалежна. Якщо ви граєте в гру 20 разів, напишіть функцію, яка описує ймовірність того, що ви виграєте 15 з 20 разів. Тут, якщо визначити$X$ як кількість виграшів, то$X$ приймає значення 0, 1, 2, 3,..., 20. Імовірність успіху є$p = 0.55$. Імовірність поломки є$q = 0.45$. Кількість випробувань - це$n = 20$. Питання ймовірності може бути викладено математично як$P(x = 15)$.

Вправа$\PageIndex{2}$

Тренер навчає дельфіна робити трюки. Імовірність того, що дельфін успішно виконає трюк, становить 35%, а ймовірність того, що дельфін не успішно виконає трюк, становить 65%. З 20 спроб хочеться знайти ймовірність того, що дельфіну вдасться 12 разів. Викладіть питання ймовірності математично.

Відповідь

$P(x = 12)$

Приклад$\PageIndex{3}$

Справедлива монета перевертається 15 разів. Кожен фліп незалежний. Яка ймовірність отримати більше десяти голів? Нехай$X =$ кількість голів в 15 сальто справедливої монети. $X$приймає значення 0, 1, 2, 3,..., 15. Так як монета справедлива,$p = 0.5$ і$q = 0.5$. Кількість випробувань - це$n = 15$. Викладіть питання ймовірності математично.

Рішення

$P(x > 10)$

Вправа$\PageIndex{4}$

Справедлива шестигранна плашка прокочується десять разів. Кожен рулон незалежний. Ви хочете знайти ймовірність прокатки одного більше трьох разів. Викладіть питання ймовірності математично.

Відповідь

$P(x > 3)$

Приклад$\PageIndex{5}$

Приблизно 70% студентів статистики роблять домашнє завдання вчасно, щоб його збирали та оцінювали. Кожен учень робить домашнє завдання самостійно. У класі статистики з 50 учнів, яка ймовірність того, що принаймні 40 вчасно виконають домашнє завдання? Студенти вибираються випадковим чином.

1. Це біноміальна проблема, оскільки є лише успіх або __________, існує фіксована кількість випробувань, а ймовірність успіху становить 0,70 для кожного випробування.
2. Якщо нас цікавить кількість учнів, які вчасно виконують домашнє завдання, то як ми визначаємо$X$?
3. Які значення$x$ набуває?
4. Що таке «провал», на словах?
5. Якщо$p + q = 1$, то що таке$q$?
6. Слова «хоча б» переводять як яка нерівність для ймовірності питання$P(x$ ____$40$).

Рішення

1. невдача
2. $X$= кількість студентів статистики, які виконують домашнє завдання вчасно
3. 0, 1, 2,..., 50
4. Невдача визначається як студент, який не виконує свою домашню роботу вчасно. Імовірність успіху є$p = 0.70$. Кількість випробувань - це$n = 50$.
5. $q = 0.30$
6. більше або дорівнює ($\geq$). Ймовірність питання є$P(x \geq 40)$.

Вправа$\PageIndex{5}$

Шістдесят п'ять відсотків людей здають державний іспит водія з першого разу. Група з 50 осіб, які склали іспит з водія, вибирається випадковим чином. Наведіть дві причини, чому це біноміальна проблема.

Відповідь

Це біноміальна проблема, оскільки є лише успіх чи невдача, і існує певна кількість випробувань. Імовірність успіху залишається однаковою для кожного судового розгляду.

Позначення для біноміала:$B =$ Binomial Probability Distribution Function

$$X \sim B(n, p)$$

Прочитайте це як "$X$є випадковою величиною з біноміальним розподілом.» Параметри є$n$ і$p$;$n =$ кількість випробувань,$p =$ ймовірність успіху на кожному дослідженні.

Приклад$\PageIndex{6}$

Було заявлено, що близько 41% дорослих працівників мають диплом середньої школи, але не продовжують жодної подальшої освіти. Якщо випадковим чином відібрано 20 дорослих працівників, знайдіть ймовірність того, що не більше 12 з них мають диплом про середню школу, але не продовжують жодної подальшої освіти. Скільки дорослих працівників ви очікуєте мати диплом середньої школи, але не продовжуєте жодної подальшої освіти?

Нехай$X$ = кількість працівників, які мають диплом середньої школи, але не продовжують жодної подальшої освіти.

$X$приймає значення 0, 1, 2,..., 20 де$n = 20, p = 0.41$, і$q = 1 – 0.41 = 0.59$. $X \sim B(20, 0.41)$

Знайти$P(x \leq 12)$. $P(x \leq 12) = 0.9738$. (калькулятор або комп'ютер)

Заходимо в ^2-й DISTR. Синтаксис інструкцій виглядає наступним чином:

Для обчислення ($x = \text{value}): \text{binompdf}(n, p, \text{number}$), якщо «число» залишилося поза увагою, результатом є біноміальна таблиця ймовірностей.

Щоб обчислити,$P(x \leq \text{value}): \text{binomcdf}(n, p, \text{number})$ якщо «число» залишилося поза увагою, результатом є кумулятивна біноміальна таблиця ймовірностей.

Для цієї проблеми: Після того, як ви перебуваєте у ^2-му DISTR, стрілка вниз до binomcdf. Натисніть клавішу ENTER. Введіть 20,0.41,12). Результат є$P(x \leq 12) = 0.9738$.

Якщо ви хочете знайти$P(x = 12)$, використовуйте pdf (binompdf). Якщо хочете знайти$P(x > 12)$, скористайтеся$1 - \text{binomcdf}(20,0.41,12)$.

Імовірність того, що максимум 12 працівників мають диплом середньої школи, але не продовжують жодної подальшої освіти, становить 0,9738.

Графік роботи$X \sim B(20, 0.41)$ виглядає наступним чином:

Малюнок$\PageIndex{1}$: Графік$X \sim B(20, 0.41)$.

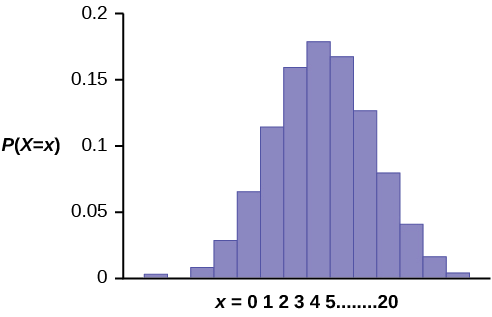
Вісь y містить ймовірність$x$, where $X =$ the number of workers who have only a high school diploma.

Кількість дорослих працівників, які ви очікуєте мати диплом середньої школи, але не продовжувати будь-яку подальшу освіту, є середнім,$\mu = np = (20)(0.41) = 8.2$.

Формула для дисперсії є$\sigma^{2} = npq$. Стандартне відхилення - це$\sigma = \sqrt{npq}$.

$$\sigma = \sqrt{(20)(0.41)(0.59)} = 2.20.$$

Вправа 4.4.5

Близько 32% учнів беруть участь у волонтерській програмі громади поза школою. Якщо 30 учнів відібрано випадковим чином, знайдіть ймовірність того, що не більше 14 з них беруть участь у волонтерській програмі громади поза школою. Скористайтеся калькулятором TI-83+ або TI-84, щоб знайти відповідь.

Відповідь

$P(x \leq 14) = 0.9695$

Приклад$\PageIndex{7}$

У каталозі художніх приладдя Jerry's Artarama 2013 року налічується 560 сторінок. На восьми сторінках розміщені виконавці підписів. Припустимо, ми випадковим чином вибірки 100 сторінок. Дозвольте$X =$ кількість сторінок, на яких розміщені виконавці підпису.

1. Які значення$x$ набуває?
2. Що таке розподіл ймовірностей? Знайдіть такі ймовірності:
   1. ймовірність того, що на двох сторінках розміщені виконавці підписів
   2. ймовірність того, що максимум на шести сторінках розміщуються виконавці підписів
   3. ймовірність того, що більш ніж на трьох сторінках розміщено підпис художників.
3. За допомогою формул обчислити (i) середнє і (ii) стандартне відхилення.

Відповідь

1. $x = 0, 1, 2, 3, 4, 5, 6, 7, 8$
2. $X \sim B(100,8560)(100,8560)$
   1. $P(x = 2) = \text{binompdf}\left(100,\dfrac{8}{560},2\right) = 0.2466$
   2. $P(x \leq 6) = \text{binomcdf}\left(100,\dfrac{8}{560},6\right) = 0.9994$
   3. $P(x > 3) = 1 – P(x \leq 3) = 1 – \text{binomcdf}\left(100,\dfrac{8}{560},3\right) = 1 – 0.9443 = 0.0557$
3. 1. Середнє$= np = (100)\left(\dfrac{8}{560}\right) = \dfrac{800}{560} \approx 1.4286$
   2. Стандартне відхилення$= \sqrt{npq} = \sqrt{(100)\left(\dfrac{8}{560}\right)\left(\dfrac{552}{560}\right)} \approx 1.1867$

Вправа$\PageIndex{7}$

Згідно з опитуванням Gallup, 60% дорослих американців вважають за краще економити, а не витрачати. Нехай$X$ = кількість дорослих американців з випадкової вибірки 50, які вважають за краще економити витрати.

1. Для чого потрібен розподіл ймовірностей$X$?
2. Скористайтеся калькулятором, щоб знайти наступні ймовірності:
   1. ймовірність того, що 25 дорослих людей у вибірці воліють економити, а не витрачати
   2. ймовірність того, що максимум 20 дорослих вважають за краще економити
   3. ймовірність того, що більше 30 дорослих людей вважають за краще економити
3. Використовуючи формули, обчислити (i) середнє і (ii) стандартне відхилення$X$.

Відповідь

1. $X \sim B(50, 0.6)$
2. Використання калькулятора TI-83, 83+, 84 з інструкціями, наведеними в прикладі:
   1. $P(x = 25) = \text{binompdf}(50, 0.6, 25) = 0.0405$
   2. $P(x \leq 20) = \text{binomcdf}(50, 0.6, 20) = 0.0034$
   3. $(x > 30) = 1 - \text{binomcdf}(50, 0.6, 30) = 1 – 0.5535 = 0.4465$
3. 1. Середнє$= np = 50(0.6) = 30$
   2. Стандартне відхилення$= \sqrt{npq} = \sqrt{50(0.6)(0.4)} \approx 3.4641$

Приклад$\PageIndex{8}$

Довічний ризик розвитку раку підшлункової залози становить приблизно один з 78 (1,28%). Припустимо, ми випадковим чином відбираємо 200 чоловік. Нехай$X$ = кількість людей, у яких буде розвиватися рак підшлункової залози.

1. Для чого потрібен розподіл ймовірностей$X$?
2. Використовуючи формули, обчислити (i) середнє і (ii) стандартне відхилення$X$.
3. Скористайтеся калькулятором, щоб знайти ймовірність того, що не більше восьми людей захворіють на рак підшлункової залози
4. Чи більш імовірно, що у п'яти-шести людей буде розвиватися рак підшлункової залози? Обґрунтуйте свою відповідь чисельно.

Відповідь

1. $X \sim B(200, 0.0128)$
2. 1. Середнє$= np = 200(0.0128) = 2.56$
   2. Стандартне відхилення$= \sqrt{npq} = \sqrt{(200)(0.0128)(0.9872)} \approx 1.5897$
3. Використання калькулятора TI-83, 83+, 84 з інструкціями, наведеними в прикладі:
   $P(x \leq 8) = \text{binomcdf}(200, 0.0128, 8) = 0.9988$
4. $P(x = 5) = \text{binompdf}(200, 0.0128, 5) = 0.0707$
   $P(x = 6) = \text{binompdf}(200, 0.0128, 6) = 0.0298$
   Отже$P(x = 5) > P(x = 6)$; більш імовірно, що п'ять людей захворіють на рак, ніж у шести.

Вправа$\PageIndex{8}$

Під час регулярного сезону НБА 2013 року ДеАндре Джордан з «Лос-Анджелес Кліпперс» мав найвищий показник завершення голів у лізі. ДеАндре забив 61,3% своїх пострілів. Припустимо, ви вибрали випадковий зразок із 80 знімків, зроблених ДеАндре протягом сезону 2013 року. Нехай кількість$X =$ пострілів, які набрали очки.

1. Для чого потрібен розподіл ймовірностей$X$?
2. Використовуючи формули, обчислити (i) середнє і (ii) стандартне відхилення$X$.
3. Скористайтеся калькулятором, щоб знайти ймовірність того, що ДеАндре забив 60 з цих пострілів.
4. Знайдіть ймовірність того, що ДеАндре забив більш ніж 50 з цих пострілів.

Відповідь

1. $X \sim B(80, 0.613)$
2. 1. Середнє$= np = 80(0.613) = 49.04$
   2. Стандартне відхилення$= \sqrt{npq} = \sqrt{80(0.613)(0.387)} \approx 4.3564$
3. Використання калькулятора TI-83, 83+, 84 з інструкціями, наведеними в прикладі:
   $P(x = 60) = \text{binompdf}(80, 0.613, 60) = 0.0036$
4. $P(x > 50) = 1 – P(x \leq 50) = 1 – \text{binomcdf}(80, 0.613, 50) = 1 – 0.6282 = 0.3718$

Приклад$\PageIndex{9}$

Наступний приклад ілюструє проблему, яка не є біноміальною. Вона порушує умову незалежності. ABC College має студентський консультативний комітет, що складається з десяти співробітників і шести студентів. Комітет бажає обрати голову і диктофон. Яка ймовірність того, що голова і реєстратор обидва студенти? Імена всіх членів комітету поміщаються в коробку, а два імена малюються без заміни. Перше намальоване ім'я визначає голову, а друге ім'я реєстратора. Є два випробування. Однак судові процеси не є незалежними, оскільки результат першого судового розгляду впливає на результат другого судового розгляду. Імовірність студента на першому розіграші є$\dfrac{6}{16}$. Імовірність учня на другому розіграші така$\dfrac{5}{15}$, коли перший розіграш вибирає студента. Імовірність така$\dfrac{6}{15}$, коли перший розіграш вибирає співробітника. Імовірність нанесення імені учня змінюється для кожного з випробувань і, отже, порушує умову незалежності.

Вправа$\PageIndex{9}$

Команда лакросу вибирає капітана. Імена всіх старших кладуть в капелюх, а перші три, які намальовані, будуть капітанами. Імена не замінюються після того, як вони намальовані (одна людина не може бути двома капітанами). Ви хочете побачити, чи всі капітани грають однакову позицію. Створіть, чи є це біноміальним чи ні, і вкажіть чому.

Відповідь

Це не є біноміальним, оскільки імена не замінюються, що означає, що ймовірність змінюється для кожного разу, коли буде намальовано ім'я. Це порушує умову незалежності.

Посилання

1. «Доступ до електроенергії (% населення)», Світовий банк, 2013. Доступно в Інтернеті за адресою http://data.worldbank.org/indicator/...first&sort=asc (доступ до 15 травня 2015 р.).
2. «Дистанційна освіта». Вікіпедія. Доступно в Інтернеті за адресою http://en.Wikipedia.org/wiki/Distance_education (доступ до 15 травня 2013 р.).
3. «Статистика НБА — 2013», ESPN НБА, 2013. Доступно в Інтернеті за адресою http://espn.go.com/nba/statistics/_/seasontype/2 (доступ до 15 травня 2013 р.).
4. Ньюпорт, Френк. «Американці все ще користуються економією, а не витратами: мало демографічних відмінностей, що спостерігаються в цих поглядах, крім доходів», GALLUP® Economy, 2013. Доступно в Інтернеті за адресою http://www.gallup.com/poll/162368/am... -spending.aspx (доступ до 15 травня 2013 р.).
5. Прайор, Джон Х., Лінда ДеАнджело, Лаура Палукі Блейк, Сільвія Уртадо, Серж Тран. Американський першокурсник: Національні норми осінь 2011. Лос-Анджелес: Спільна інституційна дослідницька програма в Науково-дослідному інституті вищої освіти в UCLA, 2011. Також доступний в Інтернеті за адресою http://heri.ucla.edu/PDFs/pubs/TFS/N...eshman2011.pdf (доступ до 15 травня 2013).
6. «Всесвітня книга фактів», Центральне розвідувальне управління. Доступно в Інтернеті за адресою https://www.cia.gov/library/publicat...k/geos/af.html (доступ до 15 травня 2013 р.).
7. «Які ключові статистичні дані щодо раку підшлункової залози?» Американське онкологічне товариство, 2013. Доступна в Інтернеті за адресою www.cancer.org/cancer/pancer/pancera... ключова статистика (доступ до 15 травня 2013).

Рецензія

Статистичний експеримент можна класифікувати як біноміальний експеримент при дотриманні наступних умов:

Є фіксована кількість випробувань,$n$.

Існує лише два можливі результати, звані «успіхом» та «невдачею» для кожного судового процесу. Буква$p$ позначає ймовірність успіху на одному випробуванні і$q$ позначає ймовірність невдачі на одному випробуванні.

$n$Випробування незалежні і повторюються з використанням однакових умов.

Результати біноміального експерименту відповідають біноміальному розподілу ймовірностей. Випадкова$X =$ величина - кількість успіхів, отриманих в$n$ незалежних випробуваннях. Середнє значення$X$ можна обчислити за формулою$\mu = np$, а стандартне відхилення задається за формулою$\sigma = \sqrt{npq}$.

Огляд формули

• $X \sim B(n, p)$означає, що дискретна випадкова величина$X$ має біноміальний розподіл ймовірностей з$n$ випробуваннями та ймовірністю успіху$p$.
• $X =$кількість успіхів у$n$ незалежних випробуваннях
• $n =$кількість незалежних випробувань
• $X$бере на себе цінності$x = 0, 1, 2, 3, \dotsc, n$
• $p =$ймовірність успіху для будь-якого судового розгляду
• $q =$ймовірність невдачі для будь-якого судового розгляду
• $p + q = 1$
• $q = 1 – p$

Середнє значення$X$ є$\mu = np$. Стандартне відхилення$X$ є$\sigma = \sqrt{npq}$.

Використовуйте наступну інформацію, щоб відповісти на наступні вісім вправ: Науково-дослідний інститут вищої освіти в UCLA зібрав дані з 203,967 вступників вперше, повний робочий день першокурсників з 270 чотирирічних коледжів та університетів США. 71,3% цих студентів відповіли, що так, вони вважають, що одностатеві пари повинні мати право на законний сімейний стан. Припустимо, що ви випадковим чином вибираєте вісім перших, повноцінних першокурсників з опитування. Вас цікавить число, яке вважає, що одностатеві пари повинні мати право на законний сімейний стан.

Вправа 4.4.9

У словах визначаємо випадкову величину$X$.

Відповідь

$X =$число, яке відповідає «yes»

Вправа 4.4.10

$X \sim$_____ (_____, _____)

Вправа 4.4.11

Які значення приймає випадкова величина$X$?

Відповідь

0, 1, 2, 3, 4, 5, 6, 7, 8

Вправа 4.4.12

Побудувати функцію розподілу ймовірностей (PDF).

$x$	$P(x)$

Вправа 4.4.13

У середньому ($\mu$), скільки ви очікуєте відповісти «так»?

Відповідь

5.7

Вправа 4.4.14

Що таке стандартне відхилення ($\sigma$)?

Вправа 4.4.15

Яка ймовірність того, що максимум п'ятеро першокурсників відповідають «так»?

Відповідь

0,4151

Вправа 4.4.16

Яка ймовірність того, що хоча б двоє першокурсників відповідають «так»?

Глосарій

Біноміальний експеримент

статистичний експеримент, який задовольняє наступним трьом умовам:

1. Є фіксована кількість випробувань,$n$.
2. Існує лише два можливі результати, які називаються «успіх» та «невдача» для кожного судового процесу. Буква$p$ позначає ймовірність успіху на одному випробуванні, і$q$ позначає ймовірність невдачі на одному випробуванні.
3. $n$Випробування незалежні і повторюються з використанням однакових умов.

Випробування Бернуллі

експеримент з наступними характеристиками:

1. Є тільки два можливі результати, які називаються «успіх» і «невдача» для кожного судового розгляду.
2. $p$Імовірність успіху однакова для будь-якого судового розгляду (тому ймовірність$q = 1 − p$ невдачі однакова для будь-якого судового розгляду).

Біноміальний розподіл ймовірностей

дискретна випадкова величина (RV), яка виникає з випробувань Бернуллі; є фіксоване число$n$, незалежних випробувань. «Незалежний» означає, що результат будь-якого судового розгляду (наприклад, пробного) не впливає на результати наступних випробувань, і всі судові процеси проводяться в однакових умовах. За цих обставин біноміальний RV$X$ визначається як кількість успіхів у$n$ випробуваннях. Позначення це:$X ~ B(n, p)$. Середнє значення є$\mu = np$ і стандартне відхилення є$\sigma = \sqrt{npq}$. Імовірність точно$x$ успіхів у$n$ випробуваннях є
$P(X = x) = {n \choose x}p^{x}q^{n-x}$.