2.5: Коробкові сюжети

Last updated
Save as PDF

Page ID: 98432

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Коробкові ділянки (також називаються ділянками коробки та вусів або ділянками коробки-вуса) дають гарне графічне зображення концентрації даних. Вони також показують, наскільки крайні значення знаходяться від більшості даних. Графік коробки будується з п'яти значень: мінімальне значення, перший квартиль, медіана, третій квартиль і максимальне значення. Ми використовуємо ці значення, щоб порівняти, наскільки близькі інші значення даних до них.

Для побудови прямокутної ділянки використовуйте горизонтальну або вертикальну цифру та прямокутну коробку. Найменші та найбільші значення даних позначають кінцеві точки осі. Перший квартиль позначає один кінець коробки, а третій квартиль позначає інший кінець коробки. Приблизно середні 50 відсотків даних потрапляють всередину коробки. «Вуса» простягаються від торців коробки до найменших і найбільших значень даних. Медіана або другий квартиль може перебувати між першим і третім квартилями, або він може бути одним, або іншим, або обома. Сюжет коробки дає хорошу, швидку картину даних.

Ви можете зіткнутися з ділянками коробки та вусів, які мають крапки, що позначають значення викидів. У тих випадках вуса не поширюються до мінімальних і максимальних значень.

Розглянемо, знову ж таки, цей набір даних.

1; 1; 2; 4; 6; 6; .8; 7.2; 8; 8.3; 9; 10; 10; 11.5

Перший квартиль - два, медіана - сім, а третій квартиль - дев'ять. Найменша величина - одна, а найбільша - 11,5. На наступному зображенні показана побудована ділянка коробки.

Дивіться інструкцію калькулятора на сайті TI або в додатку.

Перший вус горизонтального boxplot простягається від найменшого значення, 1, до першого квартиля, 2, коробка починається з першого квартилі і простягається до третього квартиля, 9, вертикальна пунктирна лінія проводиться на медіані, 7, а другий вус простягається від третього квартиля до найбільшого значення 11,5. — Малюнок\(\PageIndex{1}\)

Два вуса простягаються від першого квартилі до найменшого значення і від третього квартиля до найбільшого значення. Медіана показана пунктирною лінією.

Важливо почати графік коробки з масштабованого числового рядка. В іншому випадку ділянка коробки може не стати в нагоді.

Приклад\(\PageIndex{1}\)

Наступні дані - це висоти 40 учнів у класі статистики.

59; 60; 61; 62; 62; 63; 63; 64; 64; 64; 64; 65; 65; 65; 65; 65; 65; 65; 65; 65; 66; 66; 67; 67; 68; 69; 70; 70; 70; 70; 70; 71; 71; 72; 73; 74; 74; 75; 77

Побудувати квадратний графік з наступними властивостями; інструкції калькулятора для мінімальних і максимальних значень, а також квартилей наведені за прикладом.

Мінімальне значення = 59
Максимальне значення = 77
Q 1: Перший квартиль = 64,5
Q 2: Другий квартиль або медіана = 66
Q 3: Третій квартиль = 70

Горизонтальний boxplot з першим вусом, що простягається від найменшого значення, 59, до Q1, 64,5, коробка, починаючи від Q1 до Q3, 70, медіана пунктирною лінією на Q2, 66, і другим вусом, що простягається від Q3 до найбільшого значення, 77. — Малюнок\(\PageIndex{2}\)

Кожен квартал має приблизно 25% даних.
Спреди чотирьох кварталів складають 64,5 - 59 = 5,5 (перша чверть), 66 - 64,5 = 1,5 (друга чверть), 70 - 66 = 4 (третя чверть) та 77 - 70 = 7 (четверта чверть). Так, другий квартал має найменший спред, а четвертий квартал має найбільший спред.
\(\text{Range} = \text{maximum value} - \text{the minimum value} = 77 - 59 = 18\)
Міжквартильний діапазон:\(IQR = Q_{3} – Q_{1} = 70 - 64.5 = 5.5\).
Інтервал 59—65 має більше 25% даних, тому він має більше даних у ньому, ніж інтервал 66 через 70, який має 25% даних.
Середні 50% (середня половина) даних мають діапазон 5,5 дюймів.

Калькулятор

Щоб знайти мінімум, максимум і квартилі:

Введіть дані в редактор списків (Pres STAT 1:EDIT). Якщо вам потрібно очистити список, стрілка вгору до імені L1, натисніть CLEAR, а потім стрілку вниз.

Помістіть значення даних в список L1.

Натисніть STAT і стрілку до CALC. Натисніть 1:1 - Статистика VAR. Введіть L1.

Натисніть клавішу ENTER.

Використовуйте клавіші зі стрілками вниз і вгору для прокрутки.

Найменше значення = 59.

Найбільше значення = 77.

Q ₁: Перший квартиль = 64,5.

Q ₂: Другий квартиль або медіана = 66.

Q ₃: Третій квартиль = 70.

Для побудови ділянки коробки:

Натисніть 4: Плотсофф. Натисніть клавішу ENTER.

Стрілка вниз, а потім використовуйте клавішу зі стрілкою вправо, щоб перейти на п'яту картинку, яка є коробкою сюжету. Натисніть клавішу ENTER.

Стрілка вниз до Xlist: Натисніть 2nd 1 для L1

Стрілка вниз до частоти: натисніть альфа. Натисніть 1.

Натисніть «Збільшити». Натисніть 9: ZoomStat.

Натисніть TRACE, і використовувати клавіші зі стрілками, щоб вивчити вікно ділянки.

Вправа\(\PageIndex{1}\)

Наступні дані - це кількість сторінок в 40 книгах на полиці. Побудуйте квадратний графік за допомогою графічного калькулятора та вкажіть інтерквартильний діапазон.

136; 140; 178; 190; 205; 215; 217; 218; 232; 234; 240; 255; 270; 275; 290; 301; 303; 317; 318; 326; 333; 343; 349; 360; 369; 377; 388; 391; 392; 398; 400; 402; 408; 422; 429; 450; 475; 512

Відповідь

\(IQR = 158\)

Для деяких наборів даних деякі найбільші значення, найменше значення, перший квартиль, медіана і третій квартиль можуть бути однаковими. Наприклад, у вас може бути набір даних, в якому медіана і третій квартиль однакові. У цьому випадку діаграма не матиме пунктирної лінії всередині вікна, що відображає медіану. У правій частині вікна буде відображатися як третій квартиль, так і медіана. Наприклад, якби найменше значення і перший квартиль були обидва одиниці, медіана і третій квартиль були п'ять, а найбільше значення - сім, графік коробки виглядав би так:

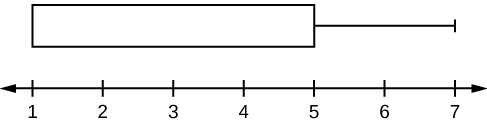
Горизонтальна коробка boxplot починається з найменшого значення і Q1, 1, поки Q3 і медіана, 5, не позначена медіана лінія, і має свій самотній вус, що простягається від Q3 до найбільшого значення, 7. — Малюнок\(\PageIndex{4}\)

При цьому не менше 25% значень дорівнюють одиниці. Двадцять п'ять відсотків значень становлять від одного до п'яти включно. Не менше 25% значень дорівнюють п'яти. Верхні 25% значень припадають на п'ять і сім включно.

Приклад\(\PageIndex{2}\)

Тестові бали для класу статистики коледжу, що проводяться протягом дня, є:

99; 56; 78; 55,5; 32; 90; 80; 81; 56; 59; 45; 77; 84.5; 84; 70; 72; 68; 32; 79; 90

Тестові бали для класу статистики коледжу, що проводиться протягом вечора, є:

98; 78; 68; 83; 81; 89; 88; 76; 65; 45; 98; 90; 80; 84,5; 85; 79; 78; 98; 90; 79; 79; 81; 25.5

Знайдіть найменші та найбільші значення, медіану та перший і третій квартиль для денного класу.
Знайдіть найменші та найбільші значення, медіану та перший і третій квартиль для нічного класу.
Для кожного набору даних, який відсоток даних знаходиться між найменшим значенням і першим квартилем? перший квартиль і медіана? медіана і третій квартиль? третій квартиль і найбільша величина? Який відсоток даних знаходиться між першим квартилем і найбільшим значенням?
Створіть графік коробки для кожного набору даних. Використовуйте один номер рядка для обох ділянок коробки.
Який квадратний сюжет має найширший розкид для середніх 50% даних (дані між першим і третім квартилями)? Що це означає для цього набору даних у порівнянні з іншим набором даних?

Відповідь

- Хв = 32
- Q ₁ = 56
- М = 74,5
- Q ₃ = 82,5
- Макс = 99
- Хв = 25,5
- Q ₁ = 78
- М = 81
- Q ₃ = 89
- Макс = 98
Денний клас: Існує шість значень даних від 32 до 56:30%. Існує шість значень даних в діапазоні від 56 до 74,5:30%. Існує п'ять значень даних в діапазоні від 74,5 до 82,5:25%. Існує п'ять значень даних в діапазоні від 82,5 до 99:25%. Є 16 значень даних між першим квартилем, 56, і найбільшим значенням, 99:75%. Нічний клас:
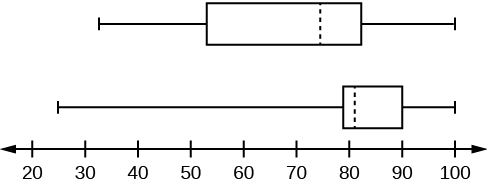
Малюнок\(\PageIndex{5}\)
Перший набір даних має більш широкий розкид для середніх 50% даних. IQR для першого набору даних більше, ніж IQR для другого набору. Це означає, що в середньому 50% першого набору даних більше мінливості.

Вправа\(\PageIndex{2}\)

Наступний набір даних показує висоту в дюймах для хлопчиків у класі з 40 студентів.

66; 66; 67; 67; 68; 68; 68; 68; 68; 68; 68; 69; 69; 69; 70; 71; 72; 72; 73; 74

Наступний набір даних показує висоту в дюймах для дівчат у класі з 40 учнів.

61; 61; 62; 62; 63; 63; 63; 65; 65; 65; 66; 66; 66; 67; 68; 68; 68; 69; 69; 69; 69

Побудуйте графічний графік за допомогою графічного калькулятора для кожного набору даних та вкажіть, який графічний графік має ширший розкид для середніх 50% даних.

Відповідь

IQR для хлопчиків = 4

IQR для дівчаток = 5

Ділянка коробки для висот дівчат має більш широкий розкид на середні 50% даних.

Приклад\(\PageIndex{3}\)

Графік графік графік коробки та вуса для показаних значень даних.

10; 10; 10; 15; 35; 75; 90; 95; 100; 175; 420; 490; 515; 515; 790

П'ять чисел, які використовуються для створення ділянки коробки та вуса:

Мін.: 10
Q ₁: 15
Мед: 95
Питання ₃: 490
Макс: 790

Наступний графік показує графік коробки і вуса.

Вправа\(\PageIndex{3}\)

Дотримуйтесь інструкцій, які ви використовували для побудови графіка графіка коробки та вуса для показаних значень даних.

0; 5; 5; 15; 30; 30; 45; 50; 50; 60; 75; 110; 140; 240; 330

Відповідь

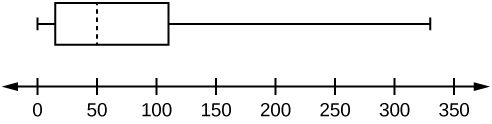
Дані знаходяться в порядку від найменшого до найбільшого. Всього 15 значень, тому восьме число по порядку - це медіана: 50. Є сім значень даних, записаних зліва від медіани і 7 значень праворуч. П'ять значень, які використовуються для створення boxplot:

Хв: 0
Q ₁: 15
Мед: 50
Питання ₃: 110
Макс: 330

Посилання

Дані з журналу West.

Рецензія

Графіки коробки - це тип графіка, який може допомогти візуально організувати дані. Для побудови графіка квадратного графіка необхідно обчислити наступні точки даних: мінімальне значення, перший квартиль, медіана, третій квартиль та максимальне значення. Після того, як графічний графік коробки, ви можете відображати та порівнювати розподіли даних.

Шістдесят п'ять випадково відібраних продавців автомобілів запитали кількість автомобілів, які вони зазвичай продають за один тиждень. Чотирнадцять людей відповіли, що вони взагалі продають три машини; дев'ятнадцять зазвичай продають чотири машини; дванадцять зазвичай продають п'ять автомобілів; дев'ять взагалі продають шість автомобілів; одинадцять зазвичай продають сім автомобілів.

Вправа 2.5.4

Побудуйте ділянку коробки нижче. Використовуйте лінійку для точного вимірювання та масштабування.

Вправа 2.5.5

Дивлячись на ваш квадратний сюжет, чи здається, що дані зосереджені разом, розподілені рівномірно або зосереджені в одних областях, але не в інших? Як ви можете сказати?

Відповідь

Більше 25% продавців продають чотири автомобілі за типовий тиждень. Ви можете побачити цю концентрацію на графіку коробки, оскільки перший квартиль дорівнює медіані. Верхні 25% і нижні 25% розподілені рівномірно; вуса мають однакову довжину.

З'єднавши його разом

Вправа 2.5.6

Округ Санта-Клара, Каліфорнія, має приблизно 27,873 японсько-американців. Їх вік такий:

Вікова група	Відсоток громади
0—17	18.9
18—24	8.0
25—34	22.8
35—44	15,0
45—54	13.1
55-64	11.9
65+	10.3

Побудувати гістограму японсько-американської спільноти в окрузі Санта-Клара, Каліфорнія. Бруски не будуть однакової ширини для цього прикладу. Чому б і ні? Який вплив це робить на достовірність графіка?
Який відсоток громади молодше 35 років?
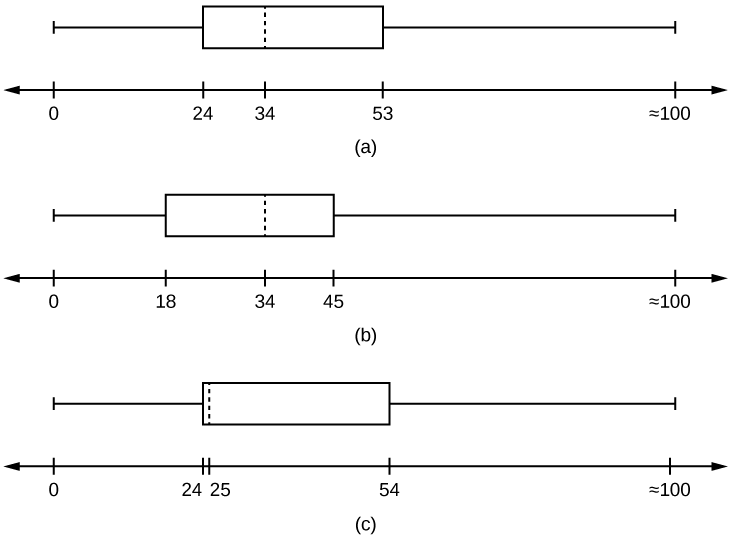
Який квадратний сюжет найбільше нагадує інформацію вище?

Три графіки коробки зі значеннями від 0 до 100. Ділянка I має Q1 на 24, M на 34, і Q3 на 53; Ділянка II має Q1 в 18, M в 34, і Q3 в 45; Ділянка III має Q1 в 24, M в 25, а Q3 в 54. — Малюнок\(\PageIndex{9}\).

Відповідь

Для графіка перевірте рішення студента.
49,7% населення — молодше 35 років.
Виходячи з інформації в таблиці, графік (а) найбільш точно представляє дані.

Глосарій

Скринька сюжет: графік, який дає швидке уявлення про середні 50% даних

Перший квартиль: значення, яке є медіаною нижньої половини впорядкованого набору даних

Багатокутник частоти: виглядає як лінійний графік, але використовує інтервали для відображення діапазонів великих обсягів даних

Інтервал: також називається інтервалом класів; інтервал представляє діапазон даних і використовується при відображенні великих наборів даних

Парний набір даних

два набори даних, які мають відношення один до одного, так що:

обидва набори даних мають однаковий розмір, і
кожна точка даних в одному наборі даних збігається з точно однією точкою з іншого набору.

Перекосений: використовується для опису даних, які не є симетричними; коли права частина графіка виглядає «відрізаною» порівняно з лівою стороною, ми говоримо, що вона «перекошена вліво». Коли ліва частина графіка виглядає «відрізаною» порівняно з правою стороною, ми говоримо, що дані «перекошені вправо». Альтернативно: коли нижчі значення даних більш поширені, ми говоримо, що дані перекошені вліво. Коли більші значення більш поширені, дані перекосуються вправо.