3.1: Типи візуалізацій
- Page ID
- 17572
Припустимо, ми хочемо вивчити склад 1,69 унцій (47,9 г) пакетів простих M&Ms. Ми отримуємо 30 мішків M&Ms (по десять з кожного з трьох магазинів) і видаляємо M&Ms з кожного пакета один за іншим, записуючи кількість синіх, коричневих, зелених, помаранчевих, червоних і жовтих M&Ms. M&Ms у перших п'яти цукерок, витягнутих з кожного мішка, і записують фактичну вагу нетто M & Ms в кожному мішку. Таблиця\(\PageIndex{1}\) узагальнює дані, зібрані на цих зразках. Ідентифікатор мішка визначає порядок, в якому мішки були відкриті та проаналізовані.
| сумка | магазин | блакитний | коричневий | зелений | помаранчевий | червоний | жовтий | жовтий_перший_п'ять | нетто_вага |
|---|---|---|---|---|---|---|---|---|---|
| 1 | CVS | 3 | 18 | 1 | 5 | 7 | 23 | 2 | 49.287 |
| 2 | CVS | 3 | 14 | 9 | 7 | 8 | 15 | 0 | 48.870 |
| 3 | Цільова | 4 | 14 | 5 | 10 | 10 | 16 | 1 | 51.250 |
| 4 | Крогер | 3 | 13 | 5 | 4 | 15 | 16 | 0 | 48.692 |
| 5 | Крогер | 3 | 16 | 5 | 7 | 8 | 18 | 1 | 48.777 |
| 6 | Крогер | 2 | 12 | 6 | 10 | 17 | 7 | 1 | 46.405 |
| 7 | CVS | 13 | 11 | 2 | 8 | 6 | 17 | 1 | 49.693 |
| 8 | CVS | 13 | 12 | 7 | 10 | 7 | 8 | 2 | 49.391 |
| 9 | Крогер | 6 | 17 | 5 | 4 | 8 | 16 | 1 | 48.196 |
| 10 | Крогер | 8 | 13 | 2 | 5 | 10 | 17 | 1 | 47.326 |
| 11 | Цільова | 9 | 20 | 1 | 4 | 12 | 13 | 3 | 50.974 |
| 12 | Цільова | 11 | 12 | 0 | 8 | 4 | 23 | 0 | 50.081 |
| 13 | CVS | 3 | 15 | 4 | 6 | 14 | 13 | 2 | 47.841 |
| 14 | Крогер | 4 | 17 | 5 | 6 | 14 | 10 | 2 | 48.377 |
| 15 | Крогер | 9 | 13 | 3 | 8 | 14 | 8 | 0 | 47.004 |
| 16 | CVS | 8 | 15 | 1 | 10 | 9 | 15 | 1 | 50.037 |
| 17 | CVS | 10 | 11 | 5 | 10 | 7 | 13 | 2 | 48.599 |
| 18 | Крогер | 1 | 17 | 6 | 7 | 11 | 14 | 1 | 48.625 |
| 19 | Цільова | 7 | 17 | 2 | 8 | 4 | 18 | 1 | 48.395 |
| 20 | Крогер | 9 | 13 | 1 | 8 | 7 | 22 | 1 | 51.730 |
| 21 | Цільова | 7 | 17 | 0 | 15 | 4 | 15 | 3 | 50.405 |
| 22 | CVS | 12 | 14 | 4 | 11 | 9 | 5 | 2 | 47.305 |
| 23 | Цільова | 9 | 19 | 0 | 5 | 12 | 12 | 0 | 49.477 |
| 24 | Цільова | 5 | 13 | 3 | 4 | 15 | 16 | 0 | 48.027 |
| 25 | CVS | 7 | 13 | 0 | 4 | 15 | 16 | 2 | 48.212 |
| 26 | Цільова | 6 | 15 | 1 | 13 | 10 | 14 | 1 | 51.682 |
| 27 | CVS | 5 | 17 | 6 | 4 | 8 | 19 | 1 | 50.802 |
| 28 | Крогер | 1 | 21 | 6 | 5 | 10 | 14 | 0 | 49.055 |
| 29 | Цільова | 4 | 12 | 6 | 5 | 13 | 14 | 2 | 46.577 |
| 30 | Цільова | 15 | 8 | 9 | 6 | 10 | 8 | 1 | 48.317 |
Зібравши наші дані, ми далі вивчаємо їх на предмет можливих проблем, таких як відсутні значення (Чи забули ми записати кількість коричневих M & Ms в будь-якому з наших зразків?) , для помилок, що вводяться, коли ми записували дані (Чи неправильно записана десяткова крапка для будь-якої з чистих ваг?) , або для незвичайних результатів (Це дійсно так, що ця сумка має тільки жовтий M & M?). Ми також вивчаємо наші дані, щоб виявити цікаві спостереження, які ми, можливо, забажаємо вивчити (Здається, що більшість ваги нетто більше, ніж вага нетто, вказана на окремих упаковках. Чому це може бути? Різниця значна?) Коли наш набір даних невеликий, ми зазвичай можемо виявити можливі проблеми та цікаві спостереження без особливих труднощів; однак для великого набору даних це стає проблемою. Замість того, щоб намагатися досліджувати окремі цінності, ми можемо подивитися на наші результати візуально. Хоча може бути важко знайти одну, непарну точку даних, коли нам доводиться індивідуально переглядати 1000 зразків, вона часто вискакує, коли ми дивимося на дані, використовуючи один або кілька підходів, які ми вивчимо в цьому розділі.
Точкові ділянки
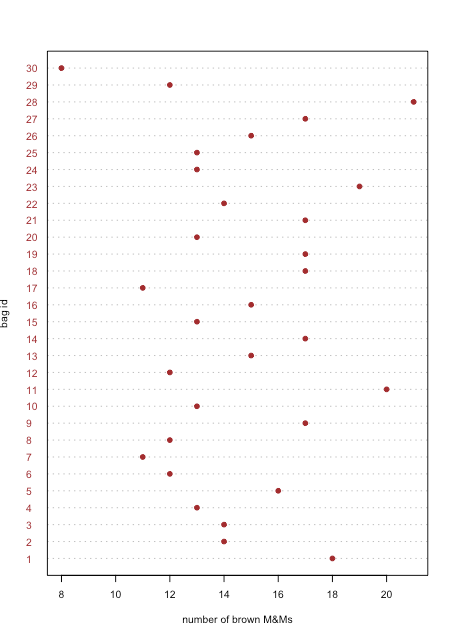
Точковий графік відображає дані для однієї змінної, причому значення кожного зразка побудовано на осі x. Окремі точки організовані вздовж осі y з першим зразком внизу і останнім зразком вгорі. \(\PageIndex{1}\)На малюнку показаний точковий графік для кількості коричневих M & Ms у 30 мішках M & Ms з табл\(\PageIndex{1}\). Розподіл точок виглядає випадковим, оскільки немає кореляції між ідентифікатором вибірки та кількістю коричневих M & Ms. Ми були б здивовані, якби виявили, що точки були розташовані від нижнього лівого до верхнього правого, оскільки це означає, що порядок, в якому ми відкриваємо мішки, визначає, чи вони мають багато або кілька коричневих M & Ms.
Стріп-діаграми
Точковий графік забезпечує швидкий спосіб дати нам впевненість у тому, що наші дані вільні від незвичайних закономірностей, але ціною простору, оскільки ми використовуємо вісь y, щоб включити ідентифікатор зразка як змінну. Stripchart використовує ту саму вісь x, як точковий графік, але не використовує вісь y для розрізнення зразків. Оскільки всі зразки з однаковою кількістю коричневих M & Ms з'являться в одному місці, що робить неможливим відрізнити їх один від одного, ми складаємо точки вертикально, щоб розкласти їх, як показано на малюнку\(\PageIndex{2}\).
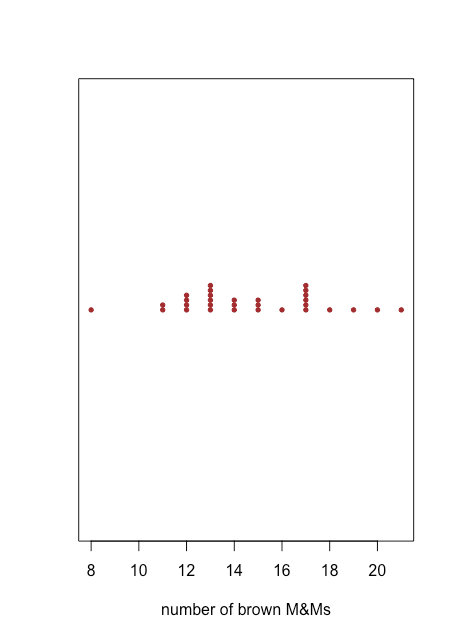
Як точковий графік на малюнку, так\(\PageIndex{1}\) і смугаста діаграма на малюнку\(\PageIndex{2}\) припускають, що існує менша щільність точок на нижній межі та верхній межі наших результатів. Ми бачимо, наприклад, що є лише одна сумка з 8, 16, 18, 19, 20 та 21 коричневим M&Ms, але є шість сумок з 13 та 17 коричневими M & Ms.
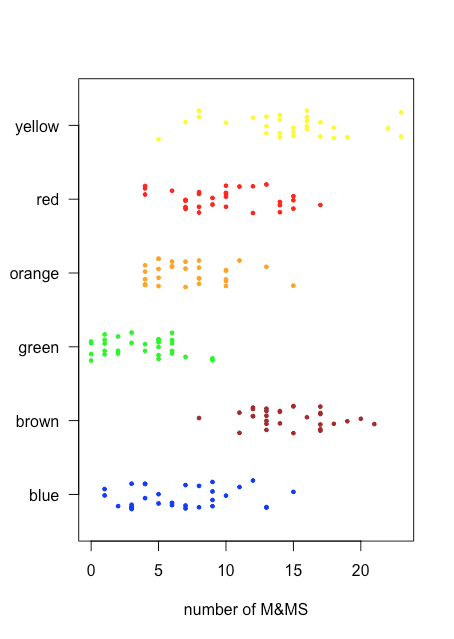
Оскільки stripchart не використовує вісь y для надання значущої категоріальної інформації, ми можемо легко відобразити кілька stripcharts одночасно. Рисунок\(\PageIndex{3}\) показує це для даних у табл\(\PageIndex{1}\). Замість того, щоб укладати окремі точки, ми перехитати їх, застосовуючи невелике випадкове зміщення до кожної точки. Серед речей, які ми дізнаємося з цієї смугової діаграми, є те, що лише коричневі та жовті M & Ms мають кількість більше 20 і що лише сині та зелені M & Ms мають кількість трьох або менше M & Ms.
Коробка і вуса ділянки
Стріп-діаграму на малюнку нам\(\PageIndex{3}\) легко вивчити, оскільки кількість зразків, 30 мішків та кількість M & Ms на мішок досить мала, щоб ми могли бачити окремі точки. У міру того, як щільність точок стає більшою, смужкова діаграма стає менш корисною. Графік коробки та вусів забезпечує подібний вигляд, але фокусується на даних з точки зору діапазону значень, що охоплюють середні 50% даних.
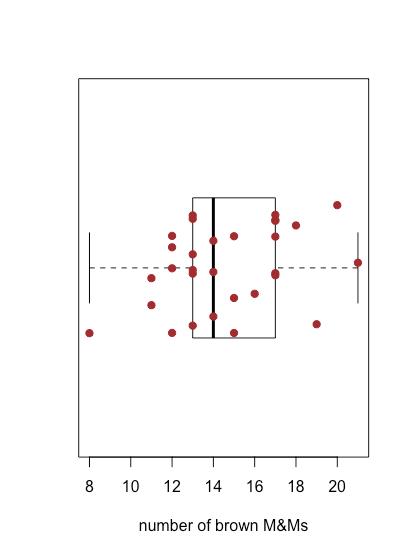
\(\PageIndex{4}\)На малюнку показано графік коробки та вуса для коричневих M&Ms, використовуючи дані в табл\(\PageIndex{1}\). 30 окремих зразків накладаються як смугаста діаграма. Центральна коробка ділить вісь x на три області: мішки з менш ніж 13 коричневими M & Ms (сім зразків), мішки з 13 і 17 коричневими M & Ms (19 зразків) та мішки з більш ніж 17 коричневими M & Ms (чотири зразки). Обмеження коробки встановлені таким чином, щоб він включав принаймні середні 50% наших даних. У цьому випадку коробка містить 19 із 30 зразків (63%) мішків, оскільки переміщення будь-якого кінця коробки до середини призводить до коробки, яка включає менше 50% зразків. Різниця між верхньою межею коробки (19) та її нижньою межею (13) називається інтерквартильним діапазоном (IQR). Товста лінія в коробці - це медіана, або середнє значення (докладніше про це і IQR в наступному розділі). Пунктирні лінії в будь-якому кінці коробки називаються вусами, і вони поширюються на найбільший або найменший результат, який знаходиться в межах\(\pm 1.5 \times \text{IQR}\) правого або лівого краю коробки відповідно.
Оскільки графік коробки та вусів не використовує вісь y для надання значущої категоріальної інформації, ми можемо легко відобразити кілька графіків у одному кадрі. Рисунок\(\PageIndex{5}\) показує це для даних у табл\(\PageIndex{1}\). Зауважте, що коли значення потрапляє за межі вуса, як це відбувається тут для жовтих M & Ms, воно позначається відображенням його як відкритого кола.
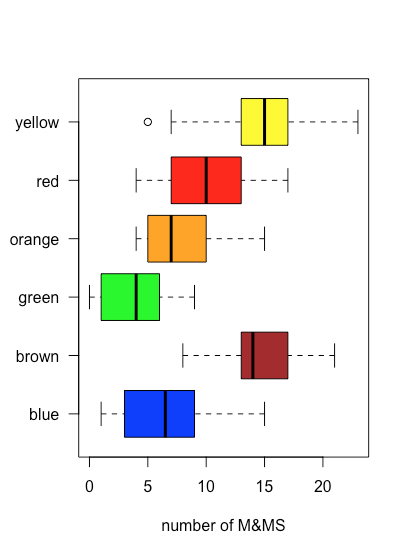
Одним із застосувань ділянки коробки та вусів є вивчення розподілу окремих зразків, особливо щодо симетрії. За винятком одиничного зразка, який потрапляє за межі вусів, розподіл жовтих M&Ms виглядає симетричним: медіана знаходиться поблизу центру коробки, а вуса простягаються однаково в обидві сторони. Розподіл помаранчевих M&Ms асиметричний: половина зразків має 4—7 M&Ms (лише чотири можливі результати), а половина - 7—15 M&Ms (дев'ять можливих результатів), що дозволяє припустити, що розподіл нахилений у бік більшої кількості помаранчевих M&Ms (див. Розділ 5 для отримання додаткової інформації про розподіл зразків).
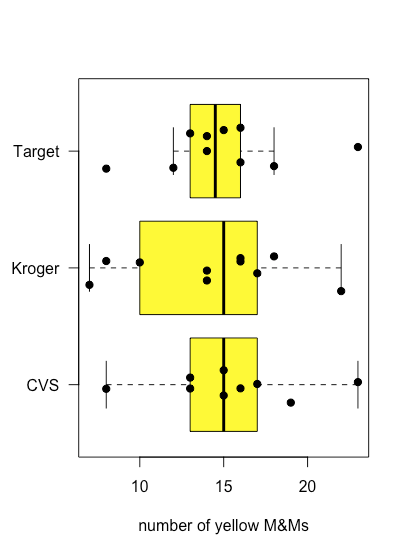
\(\PageIndex{6}\)На малюнку показані ділянки коробки та вусів для жовтих M&Ms, згруповані відповідно до магазину, де були придбані мішки M&Ms. Хоча ділянки коробки та вусів досить різні з точки зору відносних розмірів коробок та відносної довжини вусів, точкові ділянки припускають, що розподіл базових даних відносно аналогічний тим, що більшість мішків містять 12-18 жовтих M & Ms і лише кілька мішків відхиляються від ці межі. Ці спостереження обнадіюють, оскільки ми не очікуємо, що вибір магазину вплине на склад мішків M&Ms. якби ми побачили докази того, що вибір магазину вплинув на наші результати, то ми б більш уважно подивилися на самі сумки для доказів погано контрольованої змінної, наприклад типу (Чи були ми випадково придбати пакетики арахісового масла M&Ms з одного магазину?) або номер партії товару (Чи змінив виробник склад кольорів між партіями?).
Барні ділянки
Хоча точковий графік, смугова діаграма та графік коробки та вуса дають деякі якісні докази того, як розподіляються значення змінної - нам доведеться більше сказати про розподіл даних у розділі 5 - вони менш корисні, коли нам потрібна більш кількісна картина розподілу. Для цього ми можемо використовувати смуговий графік, який відображає кількість кожного дискретного результату. \(\PageIndex{7}\)На малюнку показані штрихові графіки для помаранчевого та жовтого M&Ms, використовуючи дані в таблиці\(\PageIndex{1}\).
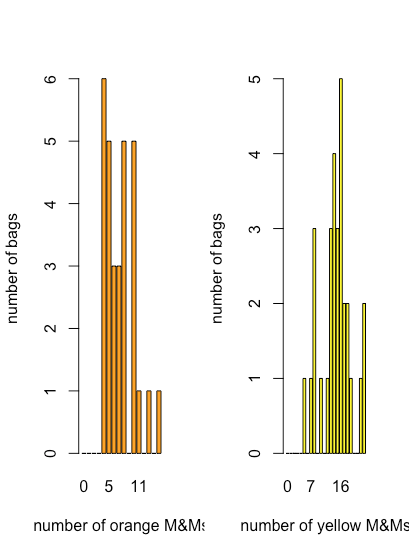
Тут ми бачимо, що найпоширеніша кількість помаранчевих M & Ms на мішок становить чотири, що також є найменшою кількістю помаранчевих M & Ms на мішок, і що спостерігається загальне зменшення кількості мішків у міру збільшення кількості помаранчевих M & M на мішок. Для жовтих M & Ms найпоширеніша кількість M & Ms на мішок становить 16, що падає поблизу середини діапазону жовтих M & Ms.
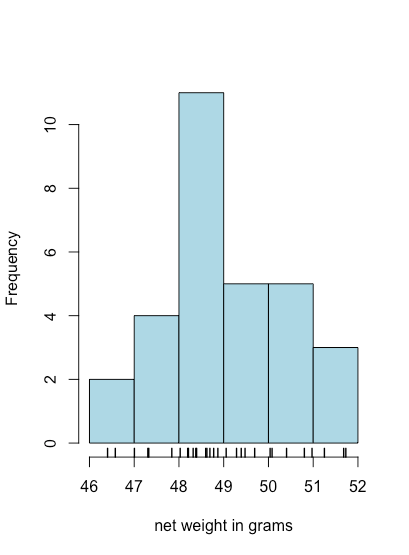
Гістограми
Графік смуги є корисним способом подивитися на розподіл дискретних результатів, таких як кількість помаранчевих або жовтих M&Ms, але це не корисно для безперервних даних, де кожен результат унікальний. Гістограма, в якій ми показуємо кількість результатів, які потрапляють у послідовність однаково розташованих контейнерів, забезпечує вигляд, подібний до вигляду штрихового графіка, але який працює з безперервними даними. На малюнку\(\PageIndex{8}\), наприклад, показана гістограма для чистих ваг 30 мішків M&Ms в табл\(\PageIndex{1}\). Окремі значення відображаються вертикальними хеш-мітками внизу гістограми.