14.8: Вступ до множинної регресії

Last updated
Save as PDF

Page ID: 98195

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Створіть рівняння регресії
Визначте «коефіцієнт регресії»
Визначте «бета-вагу»
Поясніть\(R\), що таке і як це пов'язано\(r\)
Поясніть, чому вага регресії називається «частковим нахилом»
Поясніть, чому сума квадратів, пояснена в моделі множинної регресії, зазвичай менше суми сум квадратів у простій регресії
\(R^2\)Визначте з точки зору пропорції пояснив
Тест\(R^2\) на значущість
Перевірте різницю між повною та зменшеною моделлю на значущість
Викладіть припущення множинної регресії та вкажіть, які аспекти аналізу вимагають припущень

У простій лінійній регресії передбачається змінна критерію з однієї змінної предиктора. При множинній регресії критерій прогнозується двома або більше змінними. Наприклад, у прикладному дослідженні SAT ви можете передбачити середній бал студента на основі середнього балу середньої школи (\(HSGPA\)) та їх загального балу SAT (словесний + математика). Основна ідея полягає в тому, щоб знайти лінійну комбінацію\(HSGPA\) і\(SAT\) що найкраще прогнозує університетський GPA (\(UGPA\)). Тобто, проблема полягає в тому, щоб знайти значення\(b_1\) і\(b_2\) в рівнянні, показаному нижче, які дають найкращі прогнози\(UGPA\). Як і у випадку з простою лінійною регресією, ми визначаємо найкращі прогнози як прогнози, які мінімізують квадратні помилки прогнозування.

\[UGPA' = b_1HSGPA + b_2SAT + A\]

де\(UGPA'\) передбачувана величина ВНЗ і\(A\) є постійною. Для цих даних найкраще рівняння прогнозування наведено нижче:

\[UGPA' = 0.541 \times HSGPA + 0.008 \times SAT + 0.540\]

Іншими словами, щоб обчислити прогноз балу університету студента, ви складаєте середній бал середньої школи помножений на\(0.541\), їх\(SAT\) помножене на\(0.008\), і\(0.540\). Таблиця\(\PageIndex{1}\) показує дані та прогнози для перших п'яти учнів у наборі даних.

Таблиця\(\PageIndex{1}\): Дані та прогнози
HSGPA	СИДІВ	УГПА
3.45	1232	3.38
2.78	1070	2.89
2.52	1086	2.76
3.67	1287	3.55
3.24	1130	3.19

Значення\(b\) (\(b_1\)і\(b_2\)) іноді називають «коефіцієнтами регресії», а іноді називають «регресійними вагами». Ці два терміни є синонімами.

Кратна кореляція (\(R\)) дорівнює кореляції між прогнозованими балами і фактичними балами. У цьому прикладі саме кореляція між\(UGPA'\) і\(UGPA\), яка виявляється\(0.79\). Тобто,\(R = 0.79\). Зверніть увагу, що ніколи не\(R\) буде негативним, оскільки якщо між змінними предиктора та критерієм існують негативні кореляції, ваги регресії будуть негативними, так що кореляція між прогнозованими та фактичними оцінками буде позитивною.

Інтерпретація коефіцієнтів регресії

Коефіцієнт регресії при множинній регресії - це нахил лінійної залежності між змінною критерію та частиною змінної предиктора, яка не залежить від усіх інших змінних предиктора. У цьому прикладі коефіцієнт регресії для\(HSGPA\) може бути обчислений спочатку\(HSGPA\) прогнозуванням\(SAT\) і збереженням помилок прогнозування (відмінностей між\(HSGPA\) і\(HSGPA'\)). Ці помилки прогнозування називаються «залишками», оскільки вони є тим, що залишилося\(HSGPA\) після того, як прогнози\(SAT\) віднімаються, і представляють частину,\(HSGPA\) що не залежить від\(SAT\). Ці залишки називаються\(HSGPA.SAT\), що означає, що вони є залишками\(HSGPA\) після того, як були передбачені\(SAT\). Співвідношення між\(HSGPA.SAT\) і\(SAT\) є обов'язково\(0\).

Останнім кроком обчислення коефіцієнта регресії є пошук нахилу співвідношення між цими залишками і\(UGPA\). Цей нахил є коефіцієнтом регресії для\(HSGPA\). Наступне рівняння використовується для прогнозування\(HSGPA\) з\(SAT\):

\[HSGPA' = -1.314 + 0.0036 \times SAT\]

Потім залишки обчислюються як:

\[HSGPA - HSGPA'\]

Рівняння лінійної регресії для прогнозування\(UGPA\) за залишками

\[UGPA' = 0.541 \times HSGPA.SAT + 3.173\]

Зверніть увагу, що нахил (\(0.541\)) є тим самим значенням, зазначеним раніше для\(b_1\) рівняння множинної регресії.

Це означає, що коефіцієнт регресії для\(HSGPA\) - це нахил зв'язку між змінною критерію та частиною\(HSGPA\), яка не залежить від інших змінних предиктора (не корелюється з). Він являє собою зміну змінної критерію, пов'язану зі зміною одиниці в змінній предиктора, коли всі інші змінні предиктора залишаються постійними. Оскільки коефіцієнт регресії для\(HSGPA\) є\(0.54\), це означає, що, тримаючись\(SAT\) постійною, зміна\(HSGPA\) одиниці в пов'язана зі зміною\(0.54\) в\(UGPA'\). Якби два студенти мали однакові\(SAT\) і відрізнялися\(HSGPA\) по\(2\), то ви б передбачили, що вони будуть відрізнятися\(UGPA\) по\((2)(0.54) = 1.08\). Аналогічно, якщо вони відрізнялися\(0.5\), то ви б передбачили, що вони будуть відрізнятися на\((0.50)(0.54) = 0.27\).

Нахил співвідношення між частиною змінної предиктора, незалежною від інших змінних предиктора, і критерієм є її частковий нахил. Таким чином, коефіцієнт регресії\(0.541\) for\(HSGPA\) і коефіцієнт регресії\(0.008\) for\(SAT\) є частковими нахилами. Кожен частковий нахил представляє зв'язок між змінною предиктора і критерієм, що містить постійну всі інші змінні предиктора.

Складно порівнювати коефіцієнти для різних змінних безпосередньо, оскільки вони вимірюються за різними шкалами. Різниця\(1\) в\(HSGPA\) є досить великою різницею, тоді як\(SAT\) різниця\(1\) на незначна. Тому може бути вигідно перетворити змінні так, щоб вони були в одному масштабі. Найбільш простий підхід полягає в стандартизації змінних таким чином, щоб кожен з них мав стандартне відхилення\(1\). Вага регресії для стандартизованих змінних називається «бета-вагою» і позначається грецькою літерою\(β\). Для цих даних бета-вагами є\(0.625\) і\(0.198\). Ці значення представляють зміну критерію (у стандартних відхиленнях), пов'язану зі зміною одного стандартного відхилення на предикторі [утримуючи постійну величину (и) на іншому предикторі (ах)]. Зрозуміло, що зміна одного стандартного відхилення на\(HSGPA\) пов'язане з більшою різницею, ніж зміна одного стандартного відхилення\(SAT\). У практичному плані це означає, що якщо ви знаєте студента\(HSGPA\), знання студента\(SAT\) не допомагає передбачення\(UGPA\) багато чого. Однак, якщо ви не знаєте студента\(HSGPA\), його або її\(SAT\) може допомогти в прогнозі, оскільки\(β\) вага в простому регресії передбачення\(UGPA\) від\(SAT\) є\(0.68\). Для порівняння\(β\) вага в простій регресії, що прогнозує\(UGPA\) від\(HSGPA\) є\(0.78\). Як це зазвичай буває, часткові схили менші, ніж схили в простій регресії.

Розбиття сум квадратів

Так само, як і у випадку простої лінійної регресії, сума квадратів для критерію (\(UGPA\)у цьому прикладі) може бути розділена на суму прогнозованих квадратів і суму квадратів похибки. Тобто,

\[SSY = SSY' + SSE\]

які для цих даних:

\[20.798 = 12.961 + 7.837\]

Сума передбачуваних квадратів також називається «сума квадратів, пояснених». Знову ж таки, як у випадку з простою регресією,

\[\text{Proportion Explained} = SSY'/SSY\]

У простій регресії частка дисперсії пояснюється дорівнює\(r^2\); при множинній регресії частка дисперсії пояснюється дорівнює\(R^2\).

При множинній регресії часто інформативно розділити суму квадратів, пояснену між змінними предиктора. Наприклад, сума квадратів, пояснена для цих даних, є\(12.96\). Як це значення ділиться між\(HSGPA\) і\(SAT\)? Один підхід, який, як буде видно, не працює, полягає\(UGPA\) в прогнозуванні окремих простих регресій для\(HSGPA\) і\(SAT\). Як видно з таблиці\(\PageIndex{2}\), сума квадратів в цих окремих простих регресіях дорівнює\(12.64\) for\(HSGPA\) і\(9.75\) for\(SAT\). Якщо скласти ці дві суми квадратів, ми отримаємо\(22.39\), значення набагато більше, ніж сума квадратів, пояснена\(12.96\) в множинному регресійному аналізі. Пояснення полягає в тому, що\(HSGPA\) і\(SAT\) сильно\(r = 0.78\) корелюються () і тому значна частина дисперсії в\(UGPA\) плутається між\(HSGPA\) і\(SAT\). Тобто це можна пояснити\(HSGPA\) або або\(SAT\) і підраховується двічі, якщо суми квадратів для\(HSGPA\) і просто\(SAT\) додаються.

Таблиця\(\PageIndex{2}\): Суми квадратів для різних предикторів
Провісники	Сума квадратів
HSGPA	12.64
СИДІВ	9.75
HSGPA і САТ	12.96

Таблиця\(\PageIndex{3}\) показує поділ суми квадратів на суму квадратів, однозначно пояснювану кожною змінною предиктора, сумою квадратів, плутаних між двома змінними предиктора, і сумою похибки квадратів. З цієї таблиці зрозуміло, що більша частина суми пояснених квадратів плутається між\(HSGPA\) і\(SAT\). Зауважте, що сума квадратів, однозначно пояснюється змінною предиктора, аналогічна частковому нахилу змінної, оскільки обидва передбачають зв'язок між змінною та критерієм з іншою змінною (ами), керованою.

Таблиця\(\PageIndex{3}\): Розбивка суми квадратів
Джерело	Сума квадратів	Пропорція
HSGPA (унікальний)	3.21	0,15
SAT (унікальний)	0,32	0,02
HSGPA і SAT (змішаний)	9.43	0,45
Помилка	7.84	0,38
Всього	20.80	1.00

Сума квадратів, однозначно віднесена до змінної, обчислюється шляхом порівняння двох моделей регресії: повної моделі та зменшеної моделі. Повна модель являє собою множинну регресію з усіма змінними предиктора включеними (\(HSGPA\)і\(SAT\) в цьому прикладі). Зменшена модель - це модель, яка залишає одну зі змінних предиктора. Сума квадратів, однозначно віднесена до змінної, є сумою квадратів для повної моделі мінус сума квадратів для зменшеної моделі, в якій змінна, що цікавить, опущена. Як показано в таблиці\(\PageIndex{2}\), сума квадратів для повної моделі (\(HSGPA\)і\(SAT\)) дорівнює\(12.96\). Сума квадратів для зменшеної моделі, в якій\(HSGPA\) опущено, - це просто сума квадратів, пояснена використанням\(SAT\) як змінної предиктора і є\(9.75\). Тому сума квадратів, однозначно віднесена до\(HSGPA\) є\(12.96 - 9.75 = 3.21\). Аналогічно, сума квадратів, однозначно\(SAT\) віднесена до є\(12.96 - 12.64 = 0.32\). Сума квадратів у цьому прикладі обчислюється шляхом віднімання суми квадратів, однозначно віднесеної до змінних предиктора, із суми квадратів для повної моделі:\(12.96 - 3.21 - 0.32 = 9.43\). Обчислення заплутаних сум квадратів в аналізі з більш ніж двома предикторами є більш складним і виходить за рамки цього тексту.

Оскільки дисперсія - це просто сума квадратів, розділених на ступені свободи, можна посилатися на пропорцію дисперсії, пояснену так само, як пояснюється пропорція суми квадратів. Трохи частіше посилатися на пропорцію дисперсії, поясненої, ніж пропорція суми квадратів, пояснена, і, отже, ця термінологія буде часто застосовуватися тут.

Коли змінні сильно корелюють, дисперсія, пояснена однозначно окремими змінними, може бути невеликою, хоча дисперсія, пояснена змінними разом, велика. Наприклад, хоча пропорції дисперсії пояснюються однозначно\(HSGPA\) і\(SAT\) є лише\(0.15\) і\(0.02\) відповідно, разом ці дві\(0.62\) змінні пояснюють дисперсію. Таким чином, ви можете легко недооцінити важливість змінних, якщо розглядається лише дисперсія, пояснена однозначно кожною змінною. Отже, часто корисно розглянути набір пов'язаних змінних. Наприклад, припустімо, що ви були зацікавлені в прогнозуванні продуктивності роботи з великої кількості змінних, деякі з яких відображають когнітивні здібності. Цілком ймовірно, що ці заходи когнітивних здібностей будуть сильно корелювати між собою, і тому ніхто з них не пояснить значну частину дисперсії незалежно від інших змінних. Однак ви могли б уникнути цієї проблеми, визначивши частку дисперсії, пояснену всіма змінними когнітивних здібностей, які розглядаються разом як набір. Дисперсія, пояснена множиною, буде включати всю дисперсію, однозначно пояснювану змінними у множині, а також всю дисперсію, плутану між змінними у множині. Це не буде включати дисперсію, плутану зі змінними поза множиною. Коротше кажучи, ви б обчислювали дисперсію, пояснену набором змінних, які не залежать від змінних, яких немає у множині.

Статистика інференційних

Почнемо з представлення формули перевірки значущості вкладу безлічі змінних. Потім ми покажемо, як окремі випадки цієї формули можуть бути використані для перевірки значущості, а\(R^2\) також для перевірки значущості унікального внеску окремих змінних.

Першим кроком є обчислення двох регресійних аналізів:

аналіз, в якому включені всі змінні предиктора і
аналіз, в якому змінні в наборі перевіряються змінних виключаються.

Колишня регресійна модель називається «повною моделлю», а друга - «зменшеною моделлю». Основна ідея полягає в тому, що якщо зменшена модель пояснює набагато менше, ніж повна модель, то важливий набір змінних, виключених із зменшеної моделі.

Формула тестування внеску групи змінних така:

\[F=\cfrac{\cfrac{SSQ_C-SSQ_R}{p_C-p_R}}{\cfrac{SSQ_T-SSQ_C}{N-p_C-1}}=\cfrac{MS_{explained}}{MS_{error}}\]

де:

\(SSQ_C\)сума квадратів для повної моделі,

\(SSQ_R\)сума квадратів для зменшеної моделі,

\(p_C\)кількість провісників у повній моделі,

\(p_R\)кількість предикторів в скороченій моделі,

\(SSQ_T\)- сума квадратів total (сума квадратів відхилень змінної критерію від її середнього), і

\(N\)загальна кількість спостережень

Ступені свободи для чисельника є,\(p_C - p_R\) а ступені свободи для знаменника є\(N - p_C -1\). Якщо значення значення,\(F\) то можна зробити висновок, що змінні, виключені в скороченому множині, сприяють прогнозуванню змінної критерію незалежно від інших змінних.

Ця формула може бути використана для перевірки значущості\(R^2\) шляхом визначення зменшеної моделі як не має змінних предиктора. У цьому додатку\(SSQ_R\) і\(p_R = 0\). Формула потім спрощується наступним чином:

\[F=\cfrac{\cfrac{SSQ_C}{p_C}}{\cfrac{SSQ_T-SSQ_C}{N-p_C-1}}=\cfrac{MS_{explained}}{MS_{error}}\]

який для цього прикладу стає:

\[F=\cfrac{\cfrac{12.96}{2}}{\cfrac{20.80-12.96}{105-2-1}}=\cfrac{6.48}{0.08}=84.35\]

Ступенями свободи є\(2\) і\(102\). Калькулятор\(F\) розподілу показує, що\(p < 0.001\).

F Калькулятор

Зменшена модель, яка використовується для перевірки дисперсії, поясненої однозначно одним предиктором, складається з усіх змінних, крім відповідної змінної предиктора. Наприклад, скорочена модель для тесту унікального внеску\(HSGPA\) містить лише змінну\(SAT\). Отже, сума квадратів для зменшеної моделі - це сума квадратів, коли\(UGPA\) передбачається\(SAT\). Ця сума квадратів дорівнює\(9.75\). Розрахунки для\(F\) наведені нижче:

\[F=\cfrac{\cfrac{12.96-9.75}{2-1}}{\cfrac{20.80-12.96}{105-2-1}}=\cfrac{3.212}{0.077}=41.80\]

Ступенями свободи є\(1\) і\(102\). Калькулятор\(F\) розподілу показує, що\(p < 0.001\).

Аналогічно, зменшена модель в тесті для унікального внеску\(SAT\) складається з\(HSGPA\).

\[F=\cfrac{\cfrac{12.96-12.64}{2-1}}{\cfrac{20.80-12.96}{105-2-1}}=\cfrac{0.322}{0.077}=4.19\]

Ступенями свободи є\(1\) і\(102\). Калькулятор\(F\) розподілу показує, що\(p = 0.0432\).

Тест на значущість дисперсії, що пояснюється однозначно змінною, ідентичний тесту значущості коефіцієнта регресії для цієї змінної. Коефіцієнт регресії та дисперсія, що пояснюється однозначно змінною, відображають зв'язок між змінною та критерієм, незалежним від інших змінних. Якщо дисперсія, пояснена однозначно змінною, не дорівнює нулю, то коефіцієнт регресії не може бути нульовим. Зрозуміло, що змінна з нульовим коефіцієнтом регресії не пояснила б ніякої дисперсії.

Інші статистичні дані, пов'язані з множинною регресією, виходять за рамки цього тексту. Два особливого значення мають:

довірчі інтервали на схилах регресії та
довірчі інтервали на прогнози для конкретних спостережень.

Ці інференційні статистичні дані можуть бути обчислені стандартними пакетами статистичного аналізу\(R\), такими як\(SPSS\)\(STATA\),,\(SAS\), і\(JMP\).

Вихід SPSS Вихід JMP

припущення

Ніяких припущень не потрібно для обчислення коефіцієнтів регресії або для поділу суми квадратів. Однак є кілька припущень, зроблених при інтерпретації інференційної статистики. Помірні порушення Припущень\(1-3\) не становлять серйозної проблеми для перевірки значущості змінних предиктора. Однак навіть невеликі порушення цих припущень створюють проблеми для довірчих інтервалів на прогнозах для конкретних спостережень.

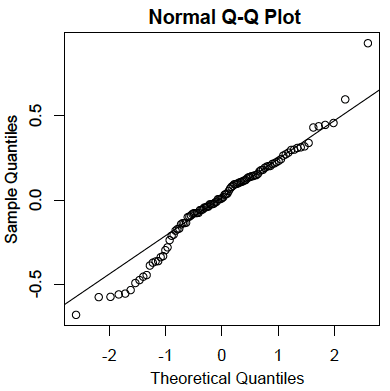
Залишки зазвичай розподіляються:

Як і у випадку з простою лінійною регресією, залишки є похибками прогнозування. Зокрема, це відмінності між фактичними балами за критерієм та прогнозованими балами. \(Q-Q\)Графік для залишків для прикладу даних наведено нижче. Цей сюжет показує, що фактичні значення даних у нижньому кінці розподілу не збільшуються настільки, як очікувалося б для нормального розподілу. Він також показує, що найбільше значення в даних вище, ніж очікувалося б для найвищого значення у вибірці такого розміру від нормального розподілу. Тим не менш, розподіл не сильно відхиляється від нормальності.

Звичайний Q-Q.png — Малюнок\(\PageIndex{1}\)\(Q-Q\): Графік для залишків для прикладу даних

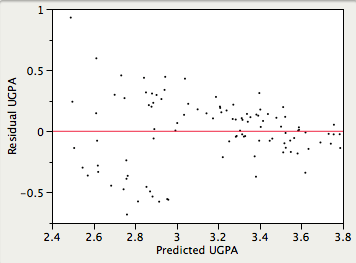
Гомоседастичність:

Передбачається, що дисперсії похибок прогнозування однакові для всіх прогнозованих значень. Як видно нижче, це припущення порушується в прикладі даних, оскільки похибки прогнозування набагато більші для спостережень з низькими та середніми прогнозованими балами, ніж для спостережень з високими прогнозованими балами. Зрозуміло, що довірчий інтервал на низькому прогнозованому\(UGPA\) буде занижувати невизначеність.

Малюнок\(\PageIndex{2}\): Низький прогнозований\(UGPA\)

Лінійність:

Передбачається, що зв'язок між кожною змінною предиктора і змінною критерію є лінійним. Якщо це припущення не виконується, то прогнози можуть систематично переоцінювати фактичні значення для одного діапазону значень на змінній предиктора і недооцінювати їх для іншого.