Skip to main content
LibreTexts - Ukrayinska

12.E: Випробування засобів (вправи)

  1. Last updated
  2. Save as PDF
  • Page ID
    98055

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Загальні питання

    Q1

    Оцінки випадкової вибірки\(8\) студентів на тесті з фізики такі:\(60, 62, 67, 69, 70, 72, 75, 78\).

    1. Перевірте, чи значно відрізняється середнє значення зразка від\(65\) на\(0.05\) рівні. Повідомте про\(t\) і\(p\) цінності.
    2. Дослідниця розуміє, що вона випадково записала рахунок, який повинен був бути\(76\) таким\(67\). Чи суттєво відрізняються ці виправлені\(65\) бали від\(0.05\) рівня? (відповідний розділ)

    Q2

    Проводиться (гіпотетичний) експеримент щодо впливу алкоголю на перцептивну рухову здатність. Десять суб'єктів перевіряються двічі, один раз після двох напоїв і один раз після двох склянок води. Два тести були в два різні дні, щоб дати алкоголю шанс стиратися. Половині випробовуваних спочатку давали алкоголь, а половину спочатку давали воду. Оцінки\(10\) предметів наведені нижче. Перше число для кожного предмета - це їх виконання в «водяному» стані. Більш високі бали відображають кращу продуктивність. Тест, щоб перевірити, чи мав алкоголь значний ефект. Повідомте про\(t\) і\(p\) цінності. (відповідний розділ)

    вода

    алкоголь

    16

    13

    15

    13

    11

    10

    20

    18

    19

    17

    14

    11

    13

    10

    15

    15

    14

    11

    16

    16

    Q3

    Оцінки на (гіпотетичному) словниковому тесті групи\(20\) річних дітей та групи\(60\) річних дітей наведені нижче.

    20 років

    60 років

    27

    26

    26

    29

    21

    29

    24

    29

    15

    27

    18

    16

    17

    20

    12

    27

    13
    1. Перевірте середню різницю значущості за допомогою\(0.05\) рівня. (відповідний розділ).
    2. Перерахуйте припущення, зроблені при обчисленні вашої відповіді. (відповідний розділ)

    Q4

    Розподіл вибірки статистики зазвичай розподіляється з оцінюваною стандартною похибкою\(12\), (\(df = 20)\).

    1. Яка ймовірність того, що ви отримали б середнє значення\(107\) (або більш екстремальне), якби параметр популяції був\(100\)? Чи значна ця ймовірність на\(0.05\) рівні (двохвоста)?
    2. Яка ймовірність того, що ви отримали б середнє\(95\) або менше (однохвостий)? Чи значна ця ймовірність на\(0.05\) рівні? Можливо, ви захочете скористатися калькулятором розподілу t для вирішення цієї проблеми. (відповідний розділ)

    Q5

    Як ви вирішуєте, чи використовувати незалежний\(t\) груповий тест або корельований\(t\) тест (тест залежних засобів)? (відповідний розділ та відповідний розділ)

    Q6

    Експеримент порівнював здатність трьох груп суб'єктів запам'ятовувати коротко представлені шахові позиції. Дані наведені нижче.

    Не-гравці

    Початківці

    Гравці турніру

    22.1

    32.5

    40.1

    22.3

    37.1

    45.6

    26.2

    39.1

    51.2

    29.6

    40.5

    56.4

    31.7

    45.5

    58.1

    33.5

    51.3

    71.1

    38.9

    52.6

    74.9

    39.7

    55.7

    75.9

    43.2

    55.9

    80.3

    43.2

    57.7

    85.3
    1. Використовуючи процедуру Tukey HSD, визначте, які групи істотно відрізняються один від одного на\(0.05\) рівні. (відповідний розділ)
    2. Тепер порівняйте кожну пару груп за допомогою\(t\) -tests. Переконайтеся, що контролюйте частоту помилок сім'ї (at\(0.05\)) за допомогою виправлення Bonferroni. Вкажіть альфа-рівень, який ви використовували.

    Q7

    Нижче наведені дані, що показують результати шести випробовуваних на тесті пам'яті. Три бали на предмет - це їх оцінки на трьох випробуваннях (\(a\)\(b\),, і\(c\)) завдання пам'яті. Чи випробовувані покращуються з кожним випробуванням? Перевірте лінійний ефект випробування для даних.

    a

    б

    c

    4

    6

    7

    3

    7

    8

    2

    8

    5

    1

    4

    7

    4

    6

    9

    2

    4

    2
    1. Обчислити\(L\) для кожного предмета, використовуючи\(-1\) контрастні ваги\(0\), і\(1\). Тобто обчислюйте\((-1)(a) + (0)(b) + (1)(c)\) для кожного предмета.
    2. Обчислити один зразок\(t\) -тест на цьому стовпці (зі\(L\) значеннями для кожного предмета), який ви створили. (відповідний розділ)

    Q8

    Учасники кидали дартс в ціль. В одному стані вони використовували свою бажану руку; в іншому стані вони використовували іншу руку. Всі суб'єкти виконувалися в обох умовах (порядок умов був врівноважений). Їх оцінки наведені нижче.

    Переважний

    Небажаний

    12

    7

    7

    9

    11

    8

    13

    10

    10

    9
    1. Який вид\(t\) -тесту слід використовувати?
    2. Обчисліть двоххвості\(t\) і\(p\) значення за допомогою цього\(t\) тесту.
    3. Обчисліть однохвосте\(t\) і\(p\) значення за допомогою цього\(t\) тесту.

    Q9

    Припустімо, що дані в попередній задачі були зібрані з використанням двох різних груп суб'єктів: одна група використовувала свою бажану руку, а інша група використовувала свою небажану руку. Проаналізуйте дані та порівняйте результати з результатами попередньої проблеми (відповідний розділ)

    Q10

    У вас є\(4\) засоби, і ви хочете порівняти кожне середнє значення з кожним іншим.

    1. Скільки всього тестів ви збираєтеся обчислити?
    2. Який був би шанс зробити принаймні одну помилку типу I, якщо помилка типу I для кожного тесту була\(0.05\) і тести були незалежними? (відповідний розділ та відповідний розділ)
    3. Чи є тести незалежними і як незалежність/ненезалежність впливають на ймовірність в (b).

    Q11

    В експерименті учасники були розділені на\(4\) групи. У кожній групі були\(20\) учасники, тому ступеня свободи (похибки) для цього дослідження були\(80 - 4 = 76\). Тест на HSD в Туреччині був проведений на даних.

    1. Обчисліть\(p\) значення для кожної пари на основі\(Q\) значення, наведеного нижче. Ви хочете використовувати калькулятор Studentized діапазону.
    2. Які відмінності значні на\(0.05\) рівні? (відповідний розділ)

    Порівняння груп

    Q

    А - Б

    3.4

    А - С

    3.8

    А - Д

    4.3

    Б - С

    1.7

    Б - Д

    3.9

    С - Д

    3.7

    Q12

    Якщо у вас є\(5\) групи у вашому дослідженні, чому б вам просто не обчислити\(t\) тест кожної групи середнього значення один з одним групою? (відповідний розділ)

    Q13

    Ви проводите дослідження, щоб побачити, чи роблять студенти краще, коли вони вивчають все відразу або з інтервалами. Одна група\(12\) учасників пройшла тест після навчання протягом однієї години безперервно. Інша група\(12\) учасників пройшла тест після навчання протягом трьох двадцятихвилинних занять. Перша група мала середній бал\(75\) і дисперсію\(120\). Друга група мала середній бал\(86\) і дисперсію\(100\).

    1. Що таке розрахункова\(t\) величина? Чи суттєво відрізняються середні бали тестів цих двох груп на\(0.05\) рівні?
    2. Якою була б\(t\) цінність, якби в кожній групі були лише\(6\) учасники? Чи були б бали значними на\(0.05\) рівні?

    Q14

    Новий тест був розроблений таким чином, щоб мати середнє значення\(80\) і стандартне відхилення\(10\). Випадкова вибірка\(20\) учнів у вашій школі здають тест, і середній бал виявляється\(85\). Чи суттєво відрізняється цей бал від\(80\)? Щоб відповісти на цю проблему, ви можете скористатися калькулятором нормального розподілу. (відповідний розділ)

    Q15

    Ви виконуєте\(t\) тест на один зразок і обчислюєте\(t\) статистику\(3.0\). Середнє значення вашого зразка було\(1.3\) і стандартне відхилення було\(2.6\). Скільки учасників було використано в цьому дослідженні? (відповідний розділ)

    Q16

    True/False: Контрасти\((-3, 1 1 1)\) і\((0, 0 , -1, 1)\) є ортогональними. (відповідний розділ)

    Q17

    True/false: Якщо ви робите\(4\) порівняння між засобами, то на основі корекції Бонферроні вам слід використовувати альфа-рівень\(0.01\) для кожного тесту. (відповідний розділ)

    Q18

    True/false:\(t\) Корельовані тести майже завжди мають більшу потужність, ніж незалежні\(t\) тести. (відповідний розділ)

    КВАРТАЛ 19

    True/false: Графік нижче представляє порушення однорідності припущення дисперсії. (відповідний розділ)

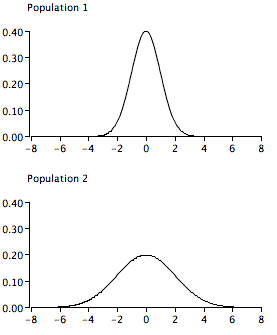
    hetero_var.gif

    Q20

    True/false: Коли ви проводите\(t\) тест на один зразок і знаєте стандартне відхилення населення, ви шукаєте критичне\(t\) значення в таблиці на основі ступенів свободи. (відповідний розділ)

    Питання з тематичних досліджень

    Наступні питання використовують дані з тематичного дослідження Angry Moods (AM).

    Q21

    (AM #17) Чи заспокоюються спортсмени чи не спортсмени більше, коли гніваються? Проведіть\(t\) тест, щоб перевірити, чи є різниця між групами в балах Control-In статистично значущою.

    Q22

    Чи мають люди взагалі вищий бал Anger-Out або Anger-In? Проведіть\(t\) тест на різницю між засобами цих двох балів. Чи є ці два засоби незалежними або залежними? (відповідний розділ)

    Наступні питання використовують дані з тематичного дослідження «Посмішки та поблажливість» (SL).

    Q23

    Порівняйте кожне середнє з нейтральним середнім. Обов'язково контролюйте частоту помилок сімейного характеру. (відповідний розділ)

    Q24

    Чи «відчувається посмішка» призводить до більшої поблажливості, ніж інші типи посмішок?

    1. Обчисліть\(L\) (лінійну комбінацію), використовуючи наступні контрастні ваги\(false: -1,\; felt: 2,\; miserable: -1,\; neutral: 0\).
    2. Виконайте тест значущості на цьому значенні\(L\). (відповідний розділ)

    Наступні питання взяті з тематичного дослідження Animal Research (AR).

    Q25

    (AR #8) Проведіть незалежний\(t\) тест зразків, порівнюючи чоловіків і жінок на переконання, що дослідження тварин необхідні. (відповідний розділ)

    Q26

    (AR #9) Виходячи з\(t\) тесту, який ви провели в попередній задачі, чи можете ви відхилити нульову гіпотезу, якщо\(alpha = 0.05\)? А як щодо того, якщо\(alpha = 0.1\)? (відповідний розділ)

    Q27

    (AR #10) Чи є якісь докази того, що\(t\) тестове припущення однорідності дисперсії порушується в\(t\) тесті, який ви обчислили в #25? (відповідний розділ)

    Наступні питання використовують дані з тематичного дослідження лікування СДУГ (AT).

    Q28

    Порівняйте кожну дозу з дозуванням нижче неї (\(d0\)\(d15\)порівняйте\(d15\) і\(d30\), і,\(d30\) і\(d60\)). Пам'ятайте, що пацієнти виконали завдання після кожного дозування.

    1. Якщо рівень помилок у сімейному відношенні є\(0.05\), який альфа-рівень ви будете використовувати для кожного порівняння під час корекції Бонферроні?
    2. Які відмінності суттєві на цьому рівні? (відповідний розділ)

    Q29

    Чи зростає продуктивність лінійно з дозуванням?

    1. Побудуйте лінійний графік цих даних.
    2. Обчислення\(L\) для кожного пацієнта. Для цього створіть нову змінну, де помножте наступні коефіцієнти на відповідні дози, а потім підсумуйте загальну суму:\((-3)d0 + (-1)d15 + (1)d30 + (3)d60\) (див. #8). Що таке середнє\(L\)?
    3. Виконайте тест на значущість на\(L\). Обчислити\(95\%\) довірчий інтервал для\(L\). (відповідний розділ)

    Виберіть відповіді

    S1

    1. \(t(7) = 1.91\)

    S4

    1. \(0.035\)

    S7

    1. двохвостий\(p = 0.0088\)

    S8

    1. \(p = 0.1662\)

    S11

    1. \(A - B: p = 0.085\)

    S13

    1. \(t(22) = 2.57\)

    S23

    \(t(76) = 3.04\)

    S25

    1. \(p = 0.0745\)

    S29

    1. \(p = 0.0006\)