3.12: Міри мінливості
- Page ID
- 98151
Цілі навчання
- Обчислити діапазон
- Обчислити дисперсію в популяції
- Обчислити стандартне відхилення від дисперсії
Що таке мінливість?
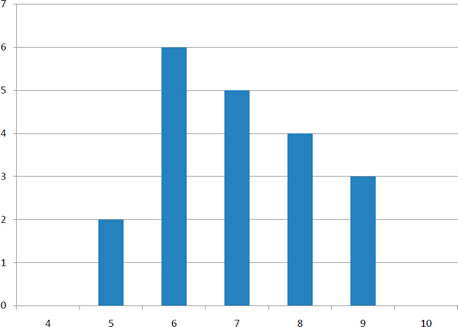
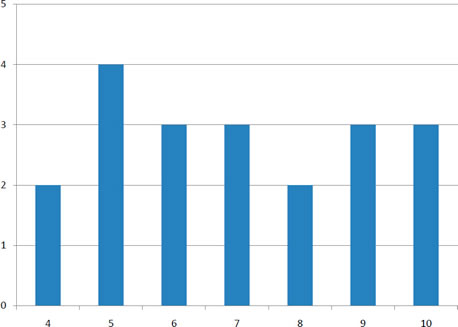
Мінливість відноситься до того, як «розкинута» група балів. Щоб побачити, що ми маємо на увазі під розкидом, розглянемо графіки на малюнку\(\PageIndex{1}\). Ці графіки представляють оцінки на двох вікторини. Середній бал для кожної вікторини є\(7.0\). Незважаючи на рівність засобів, можна помітити, що розподіли досить різні. Зокрема, оцінки на\(\text{Quiz 1}\) більш щільно упаковані, а ті\(\text{Quiz 2}\), на більш поширені. Відмінності між студентами були набагато більшими\(\text{Quiz 2}\), ніж на\(\text{Quiz 1}\).
\(\text{Quiz 1}\)
\(\text{Quiz 1}\)
Малюнок\(\PageIndex{1}\) : Гістограми двох вікторин
Терміни мінливість, поширення та дисперсія є синонімами та стосуються того, наскільки розповсюджений розподіл. Так само, як і в розділі про центральну тенденцію, де ми обговорювали заходи центру розподілу балів, в цьому розділі ми обговоримо міри мінливості розподілу. Існує чотири часто використовувані міри мінливості: діапазон, інтерквартильний діапазон, дисперсія та стандартне відхилення. У наступних кількох абзацах ми розглянемо кожну з цих чотирьох мір мінливості більш детально.
Діапазон
Діапазон - це найпростіший показник мінливості для обчислення, і той, з яким ви напевно стикалися багато разів у своєму житті. Діапазон просто найвищий бал мінус найнижчий бал. Візьмемо кілька прикладів. Який діапазон наступної групи чисел:\({10, 2, 5, 6, 7, 3, 4}\)? Ну, найбільше число\(10\), і найнижче число\(2\), так що\(10 - 2 = 8\). Асортимент є\(8\). Візьмемо інший приклад. Ось набір даних з\(10\) числами:\({99, 45, 23, 67, 45, 91, 82, 78, 62, 51}\). Що таке асортимент? Найвище число\(99\) і найменша кількість\(23\), так\(99 - 23\) дорівнює\(76\); діапазон є\(76\). Тепер розглянемо дві вікторини, показані на малюнку\(\PageIndex{1}\). На\(\text{Quiz 1}\), найнижчий бал\(5\) і найвищий бал\(9\). Тому асортимент є\(4\). Діапазон на\(\text{Quiz 2}\) був більшим: найнижчий бал був\(4\) і найвищий бал був\(10\). Тому асортимент є\(6\).
Міжквартильний діапазон
Інтерквартильний діапазон (IQR) - це діапазон середини\(50\%\) балів у розподілі. Обчислюється вона наступним чином:
\[IQR = 75^{th} percentile - 25^{th} percentile\]
Бо\(\text{Quiz 1}\),\(75^{th}\) процентиль є\(8\) і\(25^{th}\) процентиль є\(6\). Таким чином, інтерквартильний діапазон\(2\). Для\(\text{Quiz 2}\), який має більший розкид,\(75^{th}\)\(25^{th}\) процентиль є\(9\), процентиль є\(5\), а міжквартильний діапазон є\(4\). Нагадаємо, що при обговоренні коробкових ділянок\(75^{th}\) процентиль називався верхнім шарніром, а\(25^{th}\) процентиль - нижнім. Використовуючи цю термінологію, інтерквартильний діапазон називається\(H\) -spread.
Пов'язана міра мінливості називається напівінтерквартильним діапазоном. Напівінтерквартильний діапазон визначається просто як інтерквартильний діапазон, розділений на\(2\). Якщо розподіл симетричний, медіана плюс або мінус напівінтерквартильний діапазон містить половину балів у розподілі.
дисперсія
Мінливість також може бути визначена з точки зору того, наскільки близькі оцінки в розподілі до середини розподілу. Використовуючи середнє значення як міру середини розподілу, дисперсія визначається як середня квадратна різниця балів від середнього. Дані з\(\text{Quiz 1}\) наведені в табл\(\PageIndex{1}\). Середній бал є\(7.0\). Тому графа «Відхилення від середнього» містить рахунок мінус\(7\). Стовпець «Відхилення у квадраті» - це просто попередня колонка в квадраті.
| Окуляри | Відхилення від середнього | Квадратне відхилення |
|---|---|---|
| 9 | 2 | 4 |
| 9 | 2 | 4 |
| 9 | 2 | 4 |
| 8 | 1 | 1 |
| 8 | 1 | 1 |
| 8 | 1 | 1 |
| 8 | 1 | 1 |
| 7 | 0 | 0 |
| 7 | 0 | 0 |
| 7 | 0 | 0 |
| 7 | 0 | 0 |
| 7 | 0 | 0 |
| 6 | -1 | 1 |
| 6 | -1 | 1 |
| 6 | -1 | 1 |
| 6 | -1 | 1 |
| 6 | -1 | 1 |
| 6 | -1 | 1 |
| 5 | -2 | 4 |
| 5 | -2 | 4 |
| Засоби | ||
| 7 | 0 | 1.5 |
Одне, що важливо помітити, це те, що середнє відхилення від середнього є\(0\). Так буде завжди. Середнє значення відхилень в квадраті дорівнює\(1.5\). Тому дисперсія є\(1.5\). Аналогічні розрахунки з\(\text{Quiz 2}\) показують, що його дисперсія є\(6.7\). Формула для дисперсії така:
\[s^2=\frac{\sum (X-\mu )^2}{N}\]
де\(\sigma ^2\) дисперсія,\(\mu\) це середнє значення, і\(N\) число чисел. Для\(\text{Quiz 1}\),\(\mu = 7\) і\(N = 20\).
Якщо дисперсія у вибірці використовується для оцінки дисперсії в сукупності, то попередня формула занижує дисперсію і повинна використовуватися наступна формула:
\[s^2=\frac{\sum (X-M)^2}{N-1}\]
де\(s^2\) - оцінка дисперсії і\(M\) є вибірковим середнім. Зверніть увагу, що\(M\) це середнє значення вибірки, взятої з популяції із середнім значенням\(\mu\). Так як на практиці дисперсія зазвичай обчислюється в зразку, найчастіше використовується ця формула. Моделювання «оцінка дисперсії» ілюструє ухил у формулі з\(N\) в знаменнику.
Візьмемо конкретний приклад. Припустимо, що\({1, 2, 4,\: and\; 5 }\) бали були відібрані з більшої кількості населення. Щоб оцінити дисперсію в популяції, ви б обчислили\(s^2\) наступним чином:
\[M = \dfrac {1 + 2 + 4 + 5}{4} = \dfrac {12}{4} = 3\]
\[\begin{align*} s^2 &= \dfrac{[(1-3)^2 + (2-3)^2 + (4-3)^2 + (5-3)^2]}{(4-1)}\\ &= \dfrac{(4 + 1 + 1 + 4)}{3}\\ &= \dfrac{10}{3}\\ &= 3.333 \end{align*}\]
Існують альтернативні формули, які можуть бути простішими у використанні, якщо ви робите розрахунки за допомогою ручного калькулятора. Слід зазначити, що ці формули схильні до помилки округлення, якщо ваші значення дуже великі і/або у вас надзвичайно велика кількість спостережень.
\[\sigma ^2=\cfrac{\sum X^2-\cfrac{(\sum X)^2}{N}}{N}\]
і
\[s^2=\cfrac{\sum X^2-\cfrac{(\sum X)^2}{N}}{N-1}\]
Для цього прикладу,
\[\sum X^2=1^2+2^2+4^2+5^2=46\]
\[\dfrac {(\sum X)^2}{N}=\dfrac {(1+2+4+5)^2}{4}=\dfrac {144}{4}=36\]
\[\sigma ^2=\dfrac {(46-36)}{4}=2.5\]
\[s^2=\dfrac {(46-36)}{3}=3.333\; \; \text{as with the other formula}\]
Стандартне відхилення
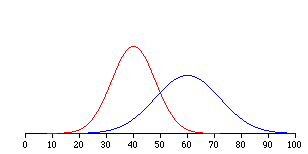
Стандартне відхилення - це просто квадратний корінь дисперсії. Це робить стандартні відхилення двох розподілів вікторини\(1.225\) і\(2.588\). Стандартне відхилення є особливо корисною мірою мінливості, коли розподіл є нормальним або приблизно нормальним (див. Розділ про нормальні розподіли), оскільки частка розподілу в межах заданої кількості стандартних відхилень від середнього може бути розрахована. Наприклад,\(68\%\) розподіл знаходиться в межах одного стандартного відхилення від середнього і приблизно\(95\%\) від розподілу знаходиться в межах двох стандартних відхилень від середнього. Тому, якби у вас був нормальний розподіл із\(50\) середнім значенням і стандартним відхиленням\(10\), то\(68\%\) розподіл був би між\(50 - 10 = 40\) і\(50 +10 =60\). Аналогічно,\(95\%\) про розподіл буде між\(50 - 2 \times 10 = 30\) і\(50 + 2 \times 10 = 70\). Символ стандартного відхилення населення є\(\sigma\); символом оцінки, обчисленої у вибірці, є\(s\). \(\PageIndex{2}\)На малюнку показані два нормальних розподілу. Червоний розподіл має середнє значення\(40\) і стандартне відхилення\(5\); синій розподіл має середнє значення\(60\) і стандартне відхилення\(10\). Для червоного розподілу\(68\%\) розподіл - між\(35\) і\(45\); для синього розподілу\(68\%\) - між\(50\) і\(70\).