ЦІЛІ НАВЧАННЯ
- Як визначаються ціни на поновлювані ресурси?
- Коли слід збирати дерева?
Дерево росте повільно, але є поновлюваним, тому аналіз розділу 11.4 «Видобуток ресурсів» не допомагає нам зрозуміти, коли вирубати дерево найвигідніше. Розглянемо збір врожаю для використання целюлози та паперу. При цьому кількість деревної тріски - це те, що має значення для рентабельності вирубування дерева, а біомаса дерева дає пряму вказівку на це. Припустимо, біомаса продається за чистою ціною р, у якої з неї віднімаються витрати на збирання та пересадку, а біомаса дерева - b (t), коли дереву t років. Це трохи спрощує аналіз, щоб використовувати безперервне дисконтування часу\(\begin{equation}\mathrm{e}-\rho \mathrm{t}=(11+r) \mathrm{t}, \text { where } \rho=\log (1+r)\end{equation}\)
Розглянемо політику вирубки дерев, коли їм Т-років. Це індукує цикл різання довжиною T. Нове дерево дасть поточну вартість прибутку
\ почати {рівняння} e −ρt pb (T) + e −2ρt pb (T) + e −3ρt pb (T) +... = e −ρ t pb (T) 1− e −ρt = pb (T) e ρ T −1. \ end {рівняння}
Цей прибуток виникає тому, що перше скорочення відбувається в момент T, при дисконтуванні e - ρ T, і дає чистий приріст pb (T). Потім процес починається спочатку, при цьому друге дерево вирубується під час 2 Т, і так далі.
Максимізація прибутку дає умову першого порядку про оптимальну довжину циклу Т
\ begin {рівняння} 0=\ математика {d}\ математика {dT}\ математика {pb} (\ математика {T})\ математика {e}\ rho\ mathrm {T} -1=\ математика {p}\ mathrm {b} ^ {\ прайм} (\ mathrm {T})\ mathrm {e}\ rho\ mathrm {T} -1-\ mathrm {pb} (\ mathrm {T})\ rho\ text {e}\ rho\ mathrm {T} (\ mathrm {e}\ rho\ mathrm {T} -1) 2\ кінець {рівняння}
Це можна переставити на врожайність
\ begin {рівняння}\ математика {b} ^ {\ прайм} (\ mathrm {T})\ математика {b} (\ mathrm {T}) =\ rho 1-\ mathrm {e} -\ rho\ mathrm {T}\ кінець {рівняння}
Ліва сторона цього рівняння - швидкість росту дерева. Права сторона - це приблизно коефіцієнт дисконтування безперервного часу, принаймні, коли T великий, оскільки це, як правило, для дерев, які зазвичай знаходяться на 20-80-річному циклі, залежно від виду. Це основа для висновку: трохи зрубати дерево, перш ніж воно виросте за процентною ставкою. Чим вище процентні ставки, тим коротший цикл, за який слід вирубувати дерева.
Використання целюлози та паперу дерев є особливим, оскільки дерево буде подрібнено на деревну тріску. Що відбувається, коли об'єкт повинен дістати дошки з дерева, а більші дошки продавати за більше? Зокрема, вигідніше отримати 4 × 4, ніж два 2 × 4с. Подвоєння діаметра дерева, що приблизно піднімає біомасу в шість-вісім разів, більше, ніж збільшує вартість деревини за рахунок збільшення біомаси.
Виявляється, наша теорія вже здатна впоратися з цією справою. Єдина адаптація - це зміна інтерпретації функції b. Тепер, замість того, щоб представляти біомасу, b (t) повинен представляти значення в дошках дерева, якому t років. (Параметр p може бути встановлений в одиницю.) Єдина поправка до правила вирубки дерев полягає в наступному: Найвигідніший момент часу спилювати дерево відбувається трохи раніше того часу, коли вартість (в дошках) дерева зростає за процентною ставкою.
Наприклад, омари стають більш цінними в міру зростання. Час максимізації прибутку для збору омарів регулюється тим же рівнянням, де b (T) - це значення омарів у віці T. Заборона врожаю омарів віком до T є засобом страхування максимального вилову омарів та запобігання перелову.
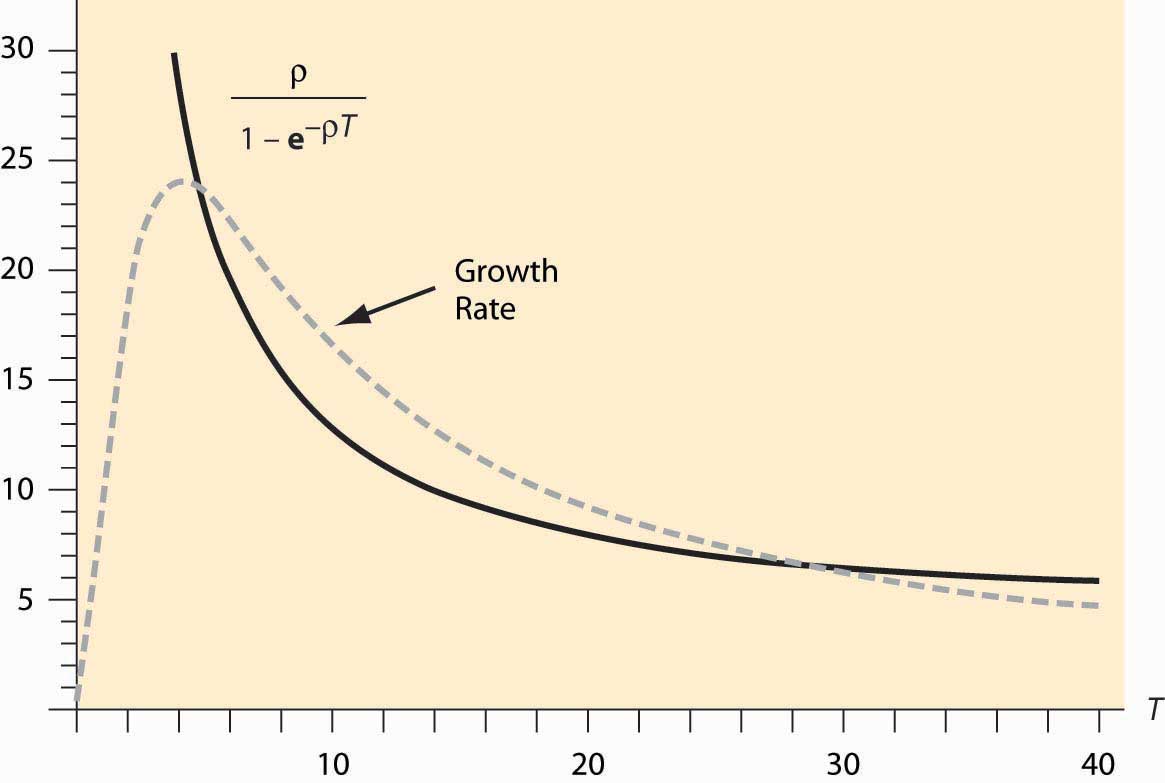
Реалізація формули проілюстрована на малюнку 11.3 «Оптимальне рішення для Т». Пунктирна лінія представляє темп зростання b ′ (T) b (T), тоді як суцільна лінія представляє ставку дисконтування, яка була встановлена на рівні 5%. Зауважте, що найкращий час для вирубки дерев - це коли їм приблизно 28, 7 років, і в той час вони ростуть на 6,5%. Малюнок 11.3 «Оптимальне рішення для T» також ілюструє ще одну особливість оптимізації - може бути кілька варіантів вирішення проблеми оптимізації, а рішення для максимізації прибутку передбачає\(\begin{equation}b^{\prime}(T) b(T)\end{equation}\) скорочення\(\begin{equation}\rho 1-\mathrm{e}-\rho \mathrm{T}\end{equation}\) зверху.
Малюнок 11.3 Оптимальне рішення для Т
Міністерство внутрішніх справ США відповідає за продаж прав на деревину на федеральних землах. Відомство використовує політику максимального сталого врожаю, щоб визначити конкретний час, коли дерево вирубують. Максимально стійкий урожай максимізує довгострокове середнє значення вирубаних дерев; тобто максимізує b (T) T.
Максимальна стійка прибутковість насправді є окремим випадком розглянутої тут політики і виникає для коефіцієнта дисконту 0. Виявляється (завдяки формулі, відомій по-різному як правило L'Hôpital або L'hospital), що\(\begin{equation}\lim \rho \rightarrow 0 \rho 1-\mathrm{e}-\rho \mathrm{T}=1 \mathrm{T}\end{equation}\).
Таким чином, правило\(\begin{equation}\mathrm{b}^{\prime}(T) \mathrm{b}(T)=\rho 1-\mathrm{e}-\rho \mathrm{T} \rightarrow 1 \mathrm{T} \text { as } \rho \rightarrow 0\end{equation}\), і це якраз те саме правило, яке виникає при максимальній стійкій врожайності.
Таким чином, Департамент внутрішніх справ діє так, ніби процентна ставка дорівнює нулю, коли її немає. Обґрунтування полягає в тому, що відділ оцінює майбутні покоління на тому ж рівні, що і нинішні покоління, тобто збільшує пропозицію для майбутніх поколінь, одночасно трохи завдаючи шкоди нинішньому поколінню покупців. Основним наслідком політики департаменту щодо максимальної стійкої врожайності є примусове різання деревини навіть тоді, коли ціни низькі під час рецесій.

