14.8: Множники Лагранжа

Last updated
Save as PDF

Page ID: 61908

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Використовувати метод множників Лагранжа для вирішення задач оптимізації з одним обмеженням.
Використовувати метод множників Лагранжа для вирішення задач оптимізації з двома обмеженнями.

Розв'язування задач оптимізації функцій двох і більше змінних може бути аналогічним вирішенню таких задач в однозмінному численні. Однак методи боротьби з декількома змінними дозволяють нам вирішувати більш різноманітні задачі оптимізації, для яких нам потрібно мати справу з додатковими умовами або обмеженнями. У цьому розділі ми розглянемо один з найбільш поширених і корисних методів вирішення задач оптимізації з обмеженнями.

Мультиплікатори Лагранжа

У попередньому розділі була досліджена прикладна ситуація, яка передбачає максимізацію функції прибутку з урахуванням певних обмежень. У цьому прикладі обмеження включали максимальну кількість м'ячів для гольфу, які можуть бути вироблені і продані в$1$ місяць$(x),$ і максимальну кількість рекламних годин, які можуть бути придбані на місяць$(y)$. Припустимо, вони були об'єднані в єдине бюджетне обмеження$20x+4y≤216$, наприклад, що враховували як витрати на виробництво м'ячів для гольфу, так і кількість рекламних годин, придбаних на місяць. Мета все ж полягає в тому, щоб максимізувати прибуток, але зараз існує інший тип обмеження на значення$x$ і$y$. Це обмеження і відповідна функція прибутку

\[f(x,y)=48x+96y−x^2−2xy−9y^2 \nonumber \]

є прикладом задачі оптимізації, а функція$f(x,y)$ називається об'єктивною функцією. Далі$f(x,y)$ йде графік різних кривих рівня функції.

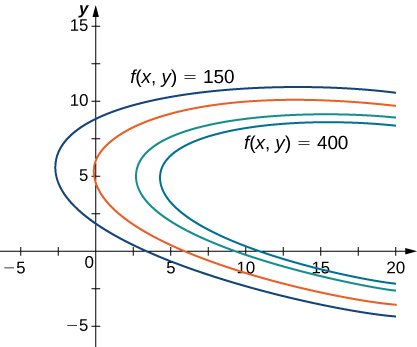
Серія обертаються еліпсів, які стають все більшими. Найменша з них маркується f (x, y) = 400, а найбільша маркується f (x, y) = 150. — Малюнок$\PageIndex{1}$: Графік, що показує криві рівня функції,$f(x,y)=48x+96y−x^2−2xy−9y^2$ що відповідають$c=150,250,350,$ і$400.$

На$\PageIndex{1}$ малюнку значення$c$ представляє різні рівні прибутку (тобто значення функції$f$). У міру$c$ збільшення значення крива зміщується вправо. Оскільки наша мета - максимізувати прибуток, ми хочемо вибрати криву якнайдалі вправо. Якби не було обмежень на кількість м'ячів для гольфу, які компанія могла б виробляти, або кількість доступних одиниць реклами, то ми могли б виробляти стільки м'ячів для гольфу, скільки хочемо, і не було б максимального прибутку для компанії. На жаль, у нас є бюджетне обмеження, яке моделюється нерівністю$20x+4y≤216.$ Щоб побачити, як це обмеження взаємодіє з функцією прибутку, на малюнку$\PageIndex{2}$ показаний графік лінії,$20x+4y=216$ накладеної на попередній графік.

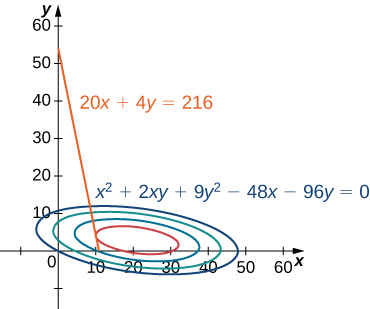
Серія обертаються еліпсів, які стають все більшими. На найменшому еліпсі, який є червоним, є дотична лінія, позначена рівнянням 20x+ 4y = 216, яка, здається, торкається еліпса поблизу (10, 4). — Малюнок$\PageIndex{2}$: Графік кривих рівня функції,$f(x,y)=48x+96y−x^2−2xy−9y^2$ що відповідає$c=150,250,350,$ і$395$. Червоний графік - це функція обмеження.

Як вже говорилося раніше, максимальний прибуток виникає, коли крива рівня знаходиться якнайдалі вправо. Однак рівень виробництва, відповідний цьому максимальному прибутку, також повинен задовольняти бюджетному обмеженню, тому точка, в якій відбувається цей прибуток, також повинна лежати на (або ліворуч) червоній лінії на малюнку$\PageIndex{2}$. Огляд цього графіка показує, що ця точка існує там, де пряма є дотичною до кривої рівня$f$. Проби і помилки виявляють, що цей рівень прибутку, здається$395$,$y$ є навколо, коли$x$ і обидва просто менше, ніж$5$. Повертаємося до вирішення цієї проблеми пізніше в цьому розділі. З теоретичної точки зору, в точці, де крива прибутку дотична до лінії обмеження, градієнт обох функцій, оцінених в цій точці, повинен вказувати в одному (або протилежному) напрямку. Нагадаємо, що градієнт функції більше однієї змінної є вектором. Якщо два вектора вказують в однакових (або протилежних) напрямках, то один повинен бути постійним кратним іншому. Ця ідея лежить в основі методу множників Лагранжа.

Метод множників Лагранжа: одне обмеження

Теорема$\PageIndex{1}$:$g$ Дозволяти$f$ і бути функції двох змінних з неперервними частинними похідними в кожній точці деякої відкритої множини$f$, що містить гладку криву$g(x,y)=0.$ Припустимо$g(x,y)=0$, що при обмеженні точками на кривій має локальний екстремум в точці$(x_0,y_0)$ і що$\vecs ∇g(x_0,y_0)≠0$. Потім йде число,$λ$ зване множником Лагранжа, для якого

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0). \nonumber \]

Доказ

Припустимо, що обмежений екстремум виникає в точці$(x_0,y_0).$ Крім того, ми припускаємо, що рівняння$g(x,y)=0$ можна плавно параметризувати як

$x=x(s) \; \text{and}\; y=y(s)$

де$s$ - параметр довжини дуги з контрольною точкою$(x_0,y_0)$ в$s=0$. Тому кількість$z=f(x(s),y(s))$ має відносний максимальний або відносний мінімум$s=0$, і це означає, що$\dfrac{dz}{ds}=0$ в цей момент. З ланцюгового правила,

\[\begin{align*} \dfrac{dz}{ds} &=\dfrac{∂f}{∂x}⋅\dfrac{∂x}{∂s}+\dfrac{∂f}{∂y}⋅\dfrac{∂y}{∂s} \\[4pt] &=\left(\dfrac{∂f}{∂x}\hat{\mathbf i}+\dfrac{∂f}{∂y}\hat{\mathbf j}\right)⋅\left(\dfrac{∂x}{∂s}\hat{\mathbf i}+\dfrac{∂y}{∂s}\hat{\mathbf j}\right)\\[4pt] &=0, \end{align*}\]

де всі похідні оцінюються на$s=0$. Однак першим фактором у точковому добутку є градієнт$f$, а другий коефіцієнт - вектор дотичної одиниці$\vec{\mathbf T}(0)$ до кривої обмеження. Оскільки точка$(x_0,y_0)$ відповідає$s=0$, то з цього рівняння випливає, що

\[\vecs ∇f(x_0,y_0)⋅\vecs{\mathbf T}(0)=0, \nonumber \]

що означає, що градієнт є або нульовим вектором,$\vecs 0$ або він є нормальним для кривої обмеження при обмеженому відносному екстремумі. Однак крива обмеження$g(x,y)=0$ є кривою рівня для функції,$g(x,y)$ так що якщо$\vecs ∇g(x_0,y_0)≠0$ потім$\vecs ∇g(x_0,y_0)$ є нормальним для цієї кривої на$(x_0,y_0)$ Це випливає, то, що є деякі скалярні$λ$ такі, що

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0) \nonumber \]

$\square$

Щоб застосувати теорему$\PageIndex{1}$ до задачі оптимізації, подібної до проблеми виробника м'ячів для гольфу, нам потрібна стратегія вирішення проблем.

Стратегія вирішення проблем: кроки для використання множників Лагранжа

Визначте$f(x,y)$ цільову функцію та функцію обмеження$g(x,y).$ Чи передбачає задача оптимізації максимізації або мінімізації цільової функції?
Налаштуйте систему рівнянь за наступним шаблоном:\[\begin{align} \vecs ∇f(x_0,y_0) &=λ\vecs ∇g(x_0,y_0) \\[4pt] g(x_0,y_0) &=0 \end{align}. \nonumber \]
Вирішити для$x_0$ і$y_0$.
Найбільша з значень$f$ при розв'язках, знайдених в кроці,$3$ максимізує$f$; найменші з цих значень мінімізуються$f$.

Приклад$\PageIndex{1}$: Using Lagrange Multipliers

Використовуйте метод множників Лагранжа, щоб знайти мінімальне значення$f(x,y)=x^2+4y^2−2x+8y$ підлягає обмеженню$x+2y=7.$

Рішення

Давайте слідувати стратегії вирішення проблем:

1. Мета функції полягає$f(x,y)=x^2+4y^2−2x+8y.$ в тому, щоб визначити функцію обмеження, ми повинні спочатку відняти$7$ з обох сторін обмеження. Це$x+2y−7=0.$ дає функцію обмеження дорівнює лівій стороні, так що$g(x,y)=x+2y−7$. Задача просить нас вирішити для мінімального значення$f$, з урахуванням обмежень (рис.$\PageIndex{3}$).

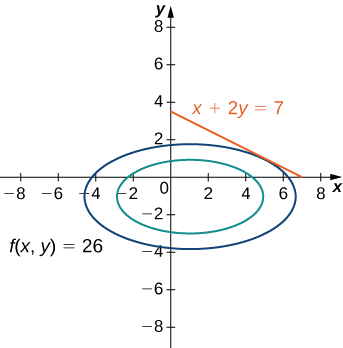
Два обертаються еліпса, один всередині іншого. На найбільшому еліпсі, який позначений f (x, y) = 26, є дотична лінія, позначена рівнянням x + 2y = 7, яка, здається, торкається еліпса поблизу (5, 1). — Малюнок$\PageIndex{3}$: Графік кривих рівня функції,$f(x,y)=x^2+4y^2−2x+8y$ що відповідає$c=10$ і$26$. Червоний графік - це функція обмеження.

2. Потім ми повинні обчислити градієнти обох$f$ і$g$:

\[\begin{align*} \vecs \nabla f \left( x, y \right) &= \left( 2x - 2 \right) \hat{\mathbf{i}} + \left( 8y + 8 \right) \hat{\mathbf{j}} \\ \vecs \nabla g \left( x, y \right) &= \hat{\mathbf{i}} + 2 \hat{\mathbf{j}}. \end{align*}\]

Рівняння$\vecs \nabla f \left( x_0, y_0 \right) = \lambda \vecs \nabla g \left( x_0, y_0 \right)$ стає

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \left( \hat{\mathbf{i}} + 2 \hat{\mathbf{j}} \right), \nonumber \]

які можна переписати як

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \hat{\mathbf{i}} + 2 \lambda \hat{\mathbf{j}}. \nonumber \]

Далі встановлюємо коефіцієнти$\hat{\mathbf{i}}$ і$\hat{\mathbf{j}}$ рівні один одному:

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda. \end{align*}\]

Рівняння$g \left( x_0, y_0 \right) = 0$ стає$x_0 + 2 y_0 - 7 = 0$. Тому система рівнянь, яку потрібно розв'язати, є

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda \\ x_0 + 2 y_0 - 7 &= 0. \end{align*}\]

3. Це лінійна система з трьох рівнянь в трьох змінних. Починаємо з вирішення другого рівняння для$λ$ і підстановки його в перше рівняння. Це дає$λ=4y_0+4$, тому підставляючи це в перше рівняння дає\[2x_0−2=4y_0+4.\nonumber \] Розв'язування цього рівняння для$x_0$ дає$x_0=2y_0+3$. Потім підставляємо це в третє рівняння:

\[\begin{align*} (2y_0+3)+2y_0−7 =0 \\[4pt]4y_0−4 =0 \\[4pt]y_0 =1. \end{align*}\]

Так як$x_0=2y_0+3,$ це дає$x_0=5.$

4. Далі, ми оцінюємо$f(x,y)=x^2+4y^2−2x+8y$ в точці$(5,1)$,\[f(5,1)=5^2+4(1)^2−2(5)+8(1)=27. \nonumber \] Щоб переконатися, що це відповідає мінімальному значенню на функцію обмеження, давайте спробуємо деякі інші точки на обмеження з обох сторін точки$(5,1)$, такі як перехоплення$g(x,y)=0$, Які є$(7,0)$ і$(0,3.5)$.

Отримуємо$f(7,0)=35 \gt 27$ і$f(0,3.5)=77 \gt 27$.

Таким чином, виявляється, що$f$ має відносний$27$ мінімум at$(5,1)$, з урахуванням заданого обмеження.

Вправа$\PageIndex{1}$

Використовуйте метод множників Лагранжа, щоб знайти максимальне значення

\[f(x,y)=9x^2+36xy−4y^2−18x−8y \nonumber \]

за умови обмеження$3x+4y=32.$

Підказка: Використовувати стратегію розв'язання задач для методу множників Лагранжа.
Відповідь: Підлягає заданому обмеженню,$f$ має максимальне значення$976$ в точці$(8,2)$.

Давайте тепер повернемося до проблеми, поставленої на початку розділу.

Приклад$\PageIndex{2}$: Golf Balls and Lagrange Multipliers

Виробник м'ячів для гольфу Pro-T розробив модель прибутку, яка залежить від$x$ кількості проданих м'ячів для гольфу на місяць (вимірюється тисячами) та кількості годин на місяць реклами y, відповідно до функції

\[z=f(x,y)=48x+96y−x^2−2xy−9y^2, \nonumber \]

де$z$ вимірюється тисячами доларів. Функція бюджетних обмежень, що стосуються витрат на виробництво тисяч м'ячів для гольфу та рекламних одиниць, дається$20x+4y=216.$ Знайти значення$x$ і$y$ які максимізувати прибуток, і знайти максимальний прибуток.

Рішення:

Знову ж таки, дотримуємося стратегії вирішення проблем:

Мета функції полягає$f(x,y)=48x+96y−x^2−2xy−9y^2.$ в тому, щоб визначити функцію обмеження, ми спочатку віднімаємо$216$ з обох сторін обмеження, потім розділити обидві сторони на$4$, що дає$5x+y−54=0.$ функція обмеження дорівнює лівій стороні, тому$g(x,y)=5x+y−54.$ проблема просить нас вирішити для максимальне значення$f$, з урахуванням цього обмеження.
Отже, ми обчислюємо градієнти обох$f$ і$g$:\[\begin{align*} \vecs ∇f(x,y) &=(48−2x−2y)\hat{\mathbf i}+(96−2x−18y)\hat{\mathbf j}\\[4pt]\vecs ∇g(x,y) &=5\hat{\mathbf i}+\hat{\mathbf j}. \end{align*}\] рівняння$\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)$ стає\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ(5\hat{\mathbf i}+\hat{\mathbf j}),\nonumber \] яке можна переписати, як\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ5\hat{\mathbf i}+λ\hat{\mathbf j}.\nonumber \] Ми потім встановлюємо коефіцієнти$\hat{\mathbf i}$ і$\hat{\mathbf j}$ рівні один одному:\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ. \end{align*}\] Рівняння$g(x_0,y_0)=0$ стає$5x_0+y_0−54=0$. Тому система рівнянь, яку потрібно розв'язати, є\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ \\[4pt]5x_0+y_0−54 =0. \end{align*}\]
Ми використовуємо ліву частину другого рівняння для заміни$λ$ в першому рівнянні:\[\begin{align*} 48−2x_0−2y_0 &=5(96−2x_0−18y_0) \\[4pt]48−2x_0−2y_0 &=480−10x_0−90y_0 \\[4pt] 8x_0 &=432−88y_0 \\[4pt] x_0 &=54−11y_0. \end{align*}\] Тоді ми підставляємо це в третє рівняння:\[\begin{align*} 5(54−11y_0)+y_0−54 &=0\\[4pt] 270−55y_0+y_0-54 &=0\\[4pt]216−54y_0 &=0 \\[4pt]y_0 &=4. \end{align*}\] Оскільки$x_0=54−11y_0,$ це дає$x_0=10.$
Потім ми підставляємо$(10,4)$ в$f(x,y)=48x+96y−x^2−2xy−9y^2,$ який дає\[\begin{align*} f(10,4) &=48(10)+96(4)−(10)^2−2(10)(4)−9(4)^2 \\[4pt] &=480+384−100−80−144 \\[4pt] &=540.\end{align*}\] Тому максимальний прибуток, який може бути досягнутий,$$540,000$ з урахуванням бюджетних обмежень, - це рівень виробництва м'ячів$10,000$ для гольфу та$4$ годин реклами, купленої на місяць. Давайте перевіримо, щоб переконатися, що це дійсно максимум. Кінцеві точки лінії, яка визначає обмеження,$(10.8,0)$ і$(0,54)$ Давайте оцінюємо$f$ в обох цих точках:\[\begin{align*} f(10.8,0) &=48(10.8)+96(0)−10.8^2−2(10.8)(0)−9(0^2) \\[4pt] &=401.76 \\[4pt] f(0,54) &=48(0)+96(54)−0^2−2(0)(54)−9(54^2) \\[4pt] &=−21,060. \end{align*}\] Друге значення являє собою втрату, оскільки не виробляються м'ячі для гольфу. Жодне з цих значень не перевищує$540$, тому здається, що наш екстремум є максимальним значенням$f$, з урахуванням заданого обмеження.

Вправа$\PageIndex{2}$: Optimizing the Cobb-Douglas function

Компанія визначила, що рівень її виробництва визначається функцією$f(x,y)=2.5x^{0.45}y^{0.55}$ Кобба-Дугласа, яка$x$ представляє загальну кількість робочих годин у$1$ році та$y$ представляє загальний капітал для компанії. Припустимо$1$ одиницю витрат праці$$40$ і$1$ одиницю капітальних витрат$$50$. Використовуйте метод множників Лагранжа, щоб знайти максимальне значення$f(x,y)=2.5x^{0.45}y^{0.55}$ підлягає бюджетному обмеженню$$500,000$ в рік.

Підказка: Використовувати стратегію розв'язання задач для методу множників Лагранжа.
Відповідь: З урахуванням даного обмеження, максимальний рівень виробництва$13890$ відбувається з$5625$ робочими годинами та$$5500$ загальним капіталом.

У випадку об'єктивної функції з трьома змінними та єдиною функцією обмеження можна також використовувати метод множників Лагранжа для розв'язання задачі оптимізації. Прикладом об'єктивної функції з трьома змінними може бути функція Кобба-Дугласа у Вправи$\PageIndex{2}$:$f(x,y,z)=x^{0.2}y^{0.4}z^{0.4},$ де$x$ представляє вартість робочої сили,$y$ представляє вкладення капіталу та$z$ представляє вартість реклами. Метод такий же, як і для методу з функцією двох змінних; рівняння, що підлягають розв'язанню

\[\begin{align*} \vecs ∇f(x,y,z) &=λ\vecs ∇g(x,y,z) \\[4pt] g(x,y,z) &=0. \end{align*}\]

Приклад$\PageIndex{3}$: Lagrange Multipliers with a Three-Variable objective function

Максимізувати функцію, що$f(x,y,z)=x^2+y^2+z^2$ підлягає обмеженню$x+y+z=1.$

Рішення

1. Мета функції полягає$f(x,y,z)=x^2+y^2+z^2.$ в тому, щоб визначити функцію обмеження, ми віднімаємо$1$ з кожної сторони обмеження:$x+y+z−1=0$ що дає функцію обмеження як$g(x,y,z)=x+y+z−1.$

2. Далі ми обчислюємо$\vecs ∇f(x,y,z)$ і$\vecs ∇g(x,y,z):$\[\begin{align*} \vecs ∇f(x,y,z) &=⟨2x,2y,2z⟩ \\[4pt] \vecs ∇g(x,y,z) &=⟨1,1,1⟩. \end{align*}\] Це призводить до рівнянь\[\begin{align*} ⟨2x_0,2y_0,2z_0⟩ &=λ⟨1,1,1⟩ \\[4pt] x_0+y_0+z_0−1 &=0 \end{align*}\], які можна переписати в наступному вигляді:\[\begin{align*} 2x_0 &=λ\\[4pt] 2y_0 &=λ \\[4pt] 2z_0 &=λ \\[4pt] x_0+y_0+z_0−1 &=0. \end{align*}\]

3. Оскільки кожне з перших трьох рівнянь має$λ$ на правій стороні, ми знаємо, що$2x_0=2y_0=2z_0$ і всі три змінні рівні один одному. Підстановка$y_0=x_0$ і$z_0=x_0$ в останнє рівняння дає$3x_0−1=0,$ так$x_0=\frac{1}{3}$$y_0=\frac{1}{3}$ і і$z_0=\frac{1}{3}$ яке відповідає критичній точці на кривій обмеження.

4. Потім ми оцінюємо$f$ в точці$\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)$:\[f\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)=\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2=\dfrac{3}{9}=\dfrac{1}{3} \nonumber \] Отже, можливий екстремум функції є$\frac{1}{3}$. Щоб переконатися, що це мінімум, виберіть інші точки, які задовольняють обмеженню з обох боків точки, яку ми отримали вище, і обчислити$f$ в цих точках. Наприклад,\[\begin{align*} f(1,0,0) &=1^2+0^2+0^2=1 \\[4pt] f(0,−2,3) &=0^2++(−2)^2+3^2=13. \end{align*}\] Обидва ці значення більше$\frac{1}{3}$, ніж, приводячи нас до думки, що екстремум є мінімумом, з урахуванням даного обмеження.

Вправа$\PageIndex{3}$

Використовуйте метод множників Лагранжа, щоб знайти мінімальне значення функції

\[f(x,y,z)=x+y+z \nonumber \]

за умови обмеження$x^2+y^2+z^2=1.$

Підказка: Використовувати стратегію розв'язання задач для методу множників Лагранжа з цільовою функцією трьох змінних.
Відповідь: Оцінка$f$ в обох точках, які ми отримали, дає нам,\[\begin{align*} f\left(\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3}\right) =\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}=\sqrt{3} \\ f\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right) =−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}=−\sqrt{3}\end{align*}\] так як обмеження є безперервним, ми порівнюємо ці значення і робимо висновок, що$f$ має відносний мінімум$−\sqrt{3}$ в точці$\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right)$, з урахуванням даного обмеження.

Проблеми з двома обмеженнями

Метод множників Лагранжа може бути застосований до задач з більш ніж одним обмеженням. В даному випадку об'єктивною функцією,$w$ є функція трьох змінних:

\[w=f(x,y,z) \nonumber \]

і вона підпорядковується двом обмеженням:

\[g(x,y,z)=0 \; \text{and} \; h(x,y,z)=0. \nonumber \]

Є два множника Лагранжа,$λ_1$ і$λ_2$, і система рівнянь стає

\[\begin{align*} \vecs ∇f(x_0,y_0,z_0) &=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0) \\[4pt] g(x_0,y_0,z_0) &=0\\[4pt] h(x_0,y_0,z_0) &=0 \end{align*}\]

Приклад$\PageIndex{4}$: Lagrange Multipliers with Two Constraints

Знайти максимальне і мінімальне значення функції

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

з урахуванням обмежень$z^2=x^2+y^2$ і$x+y−z+1=0.$

Рішення

Давайте слідувати стратегії вирішення проблем:

Мета функції полягає$f(x,y,z)=x^2+y^2+z^2.$ в тому, щоб визначити функції обмеження, ми спочатку віднімаємо$z^2$ з обох сторін першого обмеження, яке дає$x^2+y^2−z^2=0$, так$g(x,y,z)=x^2+y^2−z^2$. Друга функція обмеження:$h(x,y,z)=x+y−z+1.$
Потім ми обчислюємо градієнти$f,g,$ і$h$:\[\begin{align*} \vecs ∇f(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}+2z\hat{\mathbf k} \\[4pt] \vecs ∇g(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}−2z\hat{\mathbf k} \\[4pt] \vecs ∇h(x,y,z) &=\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}. \end{align*}\] рівняння$\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)$ стає\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=λ_1(2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}−2z_0\hat{\mathbf k})+λ_2(\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}), \nonumber \] яке може бути переписано як\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=(2λ_1x_0+λ_2)\hat{\mathbf i}+(2λ_1y_0+λ_2)\hat{\mathbf j}−(2λ_1z_0+λ_2)\hat{\mathbf k}. \nonumber \] Далі, ми встановлюємо коефіцієнти$\hat{\mathbf i}$ і$\hat{\mathbf j}$ рівні один одному:\[\begin{align*}2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2. \end{align*}\] Два рівняння, що виникають з обмежень є $z_0^2=x_0^2+y_0^2$і$x_0+y_0−z_0+1=0$. Поєднання цих рівнянь з попередніми трьома рівняннями дає\[\begin{align*} 2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2 \\[4pt]z_0^2 &=x_0^2+y_0^2 \\[4pt]x_0+y_0−z_0+1 &=0. \end{align*}\]
Перші три рівняння містять змінну$λ_2$. Розв'язування третього рівняння для$λ_2$ і заміна в перше і друге рівняння зменшує кількість рівнянь до чотирьох:\[\begin{align*}2x_0 &=2λ_1x_0−2λ_1z_0−2z_0 \\[4pt] 2y_0 &=2λ_1y_0−2λ_1z_0−2z_0\\[4pt] z_0^2 &=x_0^2+y_0^2\\[4pt] x_0+y_0−z_0+1 &=0. \end{align*}\] Далі вирішуємо перше і друге рівняння для$λ_1$. Перше рівняння дає$λ_1=\dfrac{x_0+z_0}{x_0−z_0}$, друге рівняння дає$λ_1=\dfrac{y_0+z_0}{y_0−z_0}$. Ми ставимо праву частину кожного рівняння рівною один одному і перехресно множимо:\[\begin{align*} \dfrac{x_0+z_0}{x_0−z_0} &=\dfrac{y_0+z_0}{y_0−z_0} \\[4pt](x_0+z_0)(y_0−z_0) &=(x_0−z_0)(y_0+z_0) \\[4pt]x_0y_0−x_0z_0+y_0z_0−z_0^2 &=x_0y_0+x_0z_0−y_0z_0−z_0^2 \\[4pt]2y_0z_0−2x_0z_0 &=0 \\[4pt]2z_0(y_0−x_0) &=0. \end{align*}\] Отже, або$z_0=0$ або$y_0=x_0$. Якщо$z_0=0$, то першим стає обмеження$0=x_0^2+y_0^2$. Єдиним реальним рішенням цього рівняння є$x_0=0$ і$y_0=0$, який дає впорядковану трійку$(0,0,0)$. Цей момент не задовольняє другому обмеженню, тому він не є рішенням. Далі розглянемо$y_0=x_0$, що зменшує кількість рівнянь до трьох:\[\begin{align*}y_0 &= x_0 \\[4pt] z_0^2 &= x_0^2 +y_0^2 \\[4pt] x_0 + y_0 -z_0+1 &=0. \end{align*} \nonumber \] підставляємо перше рівняння в друге і третє рівняння:\[\begin{align*} z_0^2 &= x_0^2 +x_0^2 \\[4pt] &= x_0+x_0-z_0+1 &=0. \end{align*} \nonumber \] Потім, вирішуємо друге рівняння для$z_0$, яке дає$z_0=2x_0+1$. Потім ми підставляємо це в перше рівняння\[\begin{align*} z_0^2 &= 2x_0^2 \\[4pt] (2x_0^2 +1)^2 &= 2x_0^2 \\[4pt] 4x_0^2 + 4x_0 +1 &= 2x_0^2 \\[4pt] 2x_0^2 +4x_0 +1 &=0, \end{align*}\] і використовуємо квадратичну формулу для вирішення для$x_0$:\[ x_0 = \dfrac{-4 \pm \sqrt{4^2 -4(2)(1)} }{2(2)} = \dfrac{-4\pm \sqrt{8}}{4} = \dfrac{-4 \pm 2\sqrt{2}}{4} = -1 \pm \dfrac{\sqrt{2}}{2}. \nonumber \] Відкликати$y_0=x_0$, так що це вирішує$y_0$ також. Тоді,\[z_0 = 2x_0 +1 =2 \left( -1 \pm \dfrac{\sqrt{2}}{2} \right) +1 = -2 + 1 \pm \sqrt{2} = -1 \pm \sqrt{2} . \nonumber \] отже$z_0=2x_0+1$, є два впорядкованих триплетних рішення:\[\left( -1 + \dfrac{\sqrt{2}}{2} , -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) \; \text{and} \; \left( -1 -\dfrac{\sqrt{2}}{2} , -1 -\dfrac{\sqrt{2}}{2} , -1 -\sqrt{2} \right). \nonumber \]
Ми підставляємо$\left(−1+\dfrac{\sqrt{2}}{2},−1+\dfrac{\sqrt{2}}{2}, −1+\sqrt{2}\right) $ в$f(x,y,z)=x^2+y^2+z^2$, який дає\[\begin{align*} f\left( -1 + \dfrac{\sqrt{2}}{2}, -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) &= \left( -1+\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 + \dfrac{\sqrt{2}}{2} \right)^2 + (-1+\sqrt{2})^2 \\[4pt] &= \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + (1 -2\sqrt{2} +2) \\[4pt] &= 6-4\sqrt{2}. \end{align*}\] Потім, ми підставляємо$\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2}\right)$ в$f(x,y,z)=x^2+y^2+z^2$, який дає\[\begin{align*} f\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2} \right) &= \left( -1-\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 - \dfrac{\sqrt{2}}{2} \right)^2 + (-1-\sqrt{2})^2 \\[4pt] &= \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + (1 +2\sqrt{2} +2) \\[4pt] &= 6+4\sqrt{2}. \end{align*}\]$6+4\sqrt{2}$ максимальне значення і$6−4\sqrt{2}$ є мінімальним значенням$f(x,y,z)$, з урахуванням заданих обмежень.

Вправа$\PageIndex{4}$

Використовуйте метод множників Лагранжа, щоб знайти мінімальне значення функції

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

з урахуванням обмежень$2x+y+2z=9$ і$5x+5y+7z=29.$

Підказка: Використовувати стратегію розв'язання задач для методу множників Лагранжа з двома обмеженнями.
Відповідь: $f(2,1,2)=9$є мінімальним значенням$f$, з урахуванням заданих обмежень.

Ключові концепції

Цільова функція в поєднанні з одним або декількома обмеженнями є прикладом задачі оптимізації.
Для розв'язання задач оптимізації застосовується метод множників Лагранжа, використовуючи чотириступінчасту стратегію розв'язання задач.

Ключові рівняння

Метод множників Лагранжа, одне обмеження

$\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)$

$g(x_0,y_0)=0$

Метод множників Лагранжа, два обмеження

$\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)$

$g(x_0,y_0,z_0)=0$

$h(x_0,y_0,z_0)=0$

Глосарій

обмеження: нерівність або рівняння за участю однієї або декількох змінних, яка використовується в задачі оптимізації; обмеження встановлює обмеження на можливі рішення задачі

множник Лагранжа: константа (або константи), що використовується в методі множників Лагранжа; у випадку однієї константи вона представлена змінною$λ$

метод множників Лагранжа: метод розв'язання задачі оптимізації з урахуванням одного або декількох обмежень

об'єктивна функція: функція, яка повинна бути максимізована або мінімізована в задачі оптимізації

проблема оптимізації: обчислення максимального або мінімального значення функції декількох змінних, часто з використанням множників Лагранжа

Метод множників Лагранжа: одне обмеження

Доказ

Стратегія вирішення проблем: кроки для використання множників Лагранжа

Приклад\(\PageIndex{1}\): Using Lagrange Multipliers

Вправа\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\): Golf Balls and Lagrange Multipliers

Вправа\(\PageIndex{2}\): Optimizing the Cobb-Douglas function

Приклад\(\PageIndex{3}\): Lagrange Multipliers with a Three-Variable objective function

Вправа\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\): Lagrange Multipliers with Two Constraints

Вправа\(\PageIndex{4}\)