6.6: Моменти та центри мас
- Page ID
- 61711
- Знайдіть центр маси об'єктів, розподілених уздовж лінії.
- Знайдіть центр маси тонкої пластинки.
- Використовуйте симетрію, щоб допомогти знайти центроїд тонкої пластини.
- Застосовуємо теорему Паппуса для обсягу.
У цьому розділі ми розглянемо центри мас (також звані центроїдами, при певних умовах) і моменти. Основною ідеєю центру мас є поняття точки балансування. Багато з нас бачили виконавців, які крутять пластини на кінцях палиць. Виконавці намагаються тримати кілька з них обертаються, не дозволяючи жодному з них впасти. Якщо ми подивимось на одну тарілку (не обертаючи її), на тарілці є солодка пляма, де вона ідеально балансує на палиці. Якщо ми покладемо палицю де-небудь, крім цього солодкого плями, тарілка не врівноважується, і вона падає на землю. (Ось чому виконавці крутять пластини; спина допомагає утримувати пластини від падіння, навіть якщо палиця знаходиться не зовсім в потрібному місці.) Математично це солодке пляма називається центром маси тарілки.
У цьому розділі ми спочатку розглядаємо ці поняття в одновимірному контексті, потім розширюємо наш розвиток, щоб розглянути центри мас двовимірних областей і симетрії. Останній, ми використовуємо центроїди, щоб знайти обсяг певних твердих тіл шляхом застосування теореми Паппуса.
Центр мас і моментів
Почнемо з погляду на центр маси в одновимірному контексті. Розглянемо довгу тонку дріт або стрижень мізерно малої маси, що спирається на точку опори, як показано на малюнку\(\PageIndex{1a}\). Тепер припустимо, ми розміщуємо об'єкти, що мають маси\(m_1\)\(d_1\) і\(m_2\) на відстанях і\(d_2\) від точки опори відповідно, як показано на малюнку\(\PageIndex{1b}\).
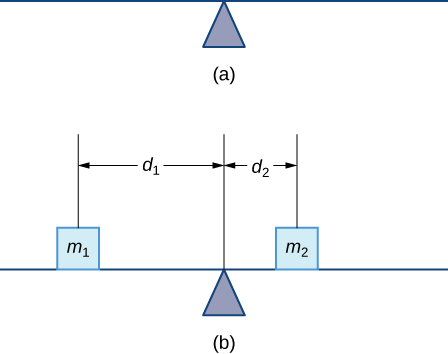
Найбільш поширеним реальним прикладом такої системи є гойдалки на ігровому майданчику, або teeter-totter, коли діти різної ваги сидять на різній відстані від центру. На гойдалках, якщо одна дитина сидить на кожному кінці, важча дитина опускається вниз, а легша дитина піднімається в повітря. Якщо важча дитина ковзає у напрямку до центру, хоча, гойдалки балансує. Застосовуючи це поняття до мас на стрижні, відзначимо, що маси врівноважують один одного тоді і тільки тоді, коли
\[m_1d_1=m_2d_2. \nonumber \]
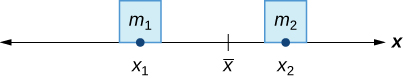
У прикладі гойдалок ми врівноважували систему, переміщуючи маси (дітей) щодо точки опори. Однак нас дійсно цікавлять системи, в яких маси не дозволяють рухатися, а замість цього ми збалансуємо систему, рухаючи точку опори. Припустимо, у нас є дві точкові маси\(m_2\),\(m_1\) причому, розташовані на числовій лінії в точках\(x_1\) і\(x_2\), відповідно (рис.\(\PageIndex{2}\)). Центр маси - це точка\(\bar{x}\), де слід розмістити точку опори, щоб зробити баланс системи.
Таким чином, ми маємо
\[ \begin{align*} m_1|x_1−\bar{x}| &=m_2|x_2−\bar{x}| \\[4pt] m_1(\bar{x}−x_1) &=m_2(x_2−\bar{x}) \\[4pt] m_1\bar{x}−m_1x_1 &=m_2x_2−m_2\bar{x} \\[4pt] \bar{x}(m_1+m_2) &=m_1x_1+m_2x_2 \end{align*} \nonumber \]
або
\[ \bar{x} =\dfrac{m_1x_1+m_2x_2}{m_1+m_2} \label{COM} \]
Вираз в чисельнику Equation\ ref {COM}\(m_1x_1+m_2x_2\), називається першим моментом системи щодо походження. Якщо контекст зрозумілий, ми часто скидаємо слово першим і просто називаємо цей вираз моментом системи. Вираз в знаменнику,\(m_1+m_2\), - це загальна маса системи. Таким чином, центр мас системи - це точка, в якій можна було б сконцентрувати загальну масу системи, не змінюючи моменту.
Ця ідея не обмежується лише двома точковими масами. Загалом, якщо\(n\) маси,\(m_1,m_2,…,m_n,\) розміщуються на числовій лінії в точках\(x_1,x_2,…,x_n,\) відповідно, то центр мас системи задається
\[ \bar{x}=\dfrac{\displaystyle {\sum_{i=1}^nm_ix_i}}{\displaystyle {\sum_{i=1}^nm_i}} \nonumber \]
\(m_1,m_2,…,m_n\)Дозволяти точкові маси, розміщені на числовій лінії в точках\(x_1,x_2,…,x_n\), відповідно, і нехай\(\displaystyle m=\sum_{i=1}^nm_i\) позначають загальну масу системи. Потім момент системи щодо походження задається
\[M=\sum_{i=1}^nm_ix_i \label{moment} \]
а центр маси системи задається
\[\bar{x}=\dfrac{M}{m}. \label{COM2a} \]
Ми застосуємо цю теорему в наступному прикладі.
Припустимо, чотири точкові маси розміщуються на числовій лінії наступним чином:
- \(m_1=30\,kg,\)розміщений на\(x_1=−2m\)
- \(m_2=5\,kg,\)розміщений на\(x_2=3m\)
- \(m_3=10\,kg,\)розміщений на\(x_3=6m\)
- \(m_4=15\,kg,\)розміщений на\(x_4=−3m.\)
Рішення
Знайдіть момент системи щодо походження і знайдіть центр мас системи.
Для початку нам потрібно обчислити момент системи (Equation\ ref {moment}):
\[ \begin{align*} M &=\sum_{i=1}^4m_ix_i \\[4pt] &= −60+15+60−45 \\[4pt] &=−30. \end{align*}\]
Тепер, щоб знайти центр мас, нам знадобиться загальна маса системи:
\[ \begin{align*} m &=\sum_{i=1}^4m_i \\[4pt] &=30+5+10+15 \\[4pt] &= 60\, kg \end{align*}\]
Тоді ми маємо (від Рівняння\ ref {coM2a})
\(\bar{x}–=\dfrac{M}{m}=−\dfrac{30}{60}=−\dfrac{1}{2}\).
Центр маси розташований на 1/2 м зліва від початку.
Припустимо, чотири точкові маси розміщуються на числовій лінії наступним чином:
- \(m_1=12\,kg\)розміщений на\(x_1=−4m\)
- \(m_2=12\,kg\)розміщений на\(x_2=4m\)
- \(m_3=30\,kg\)розміщений на\(x_3=2m\)
- \(m_4=6\,kg,\)розміщений на\(x_4=−6m.\)
Знайдіть момент системи щодо походження і знайдіть центр мас системи.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
\(M=24,\bar{x}=\dfrac{2}{5}m\)
Ми можемо узагальнити це поняття, щоб знайти центр мас системи точкових мас у площині. \(m_1\)Дозволяти точка маса розташована\((x_1,y_1)\) в точці в площині. Потім момент\(M_x\) маси по відношенню до\(x\) -осі задається по\(M_x=m_1y_1\). Аналогічно момент\(M_y\) по відношенню до\(y\) -осі задається
\[M_y=m_1x_1. \nonumber \]
Зверніть увагу, що\(x\) -координата точки використовується для обчислення моменту щодо\(y\) -осі, і навпаки. Причина в тому, що\(x\) -координата дає відстань від маси точки до\(y\) -осі, а\(y\) -координата дає відстань до\(x\) -осі (див. Наступний малюнок).

Якщо у нас є кілька точкових мас у\(xy\) -площині, ми можемо використовувати моменти щодо\(x\) - і\(y\) -осей для обчислення\(x\) - і\(y\) -координат центру маси системи.
Дозволяти\(m_1\)\(m_2\),,...,\(m_n\) бути точковими масами, розташованими в\(xy\) -площині в точках\((x_1,y_1),(x_2,y_2),…,(x_n,y_n),\) відповідно, і нехай\(\displaystyle m=\sum_{i=1}^nm_i\) позначають загальну масу системи. Тоді моменти\(M_x\) і\(M_y\) системи щодо\(x\) - і\(y\) -осей, відповідно, задаються
\[M_x=\sum_{i=1}^nm_iy_i \label{COM1} \]
і
\[M_y=\sum_{i=1}^nm_ix_i. \label{COM2} \]
Також координатами центру мас\((\bar{x},\bar{y})\) системи є
\[\bar{x}=\dfrac{M_y}{m} \label{COM3} \]
і
\[\bar{y}=\dfrac{M_x}{m}. \label{COM4} \]
Наступний приклад демонструє, як до центру маси можуть застосовуватися формули (Equations\ ref {COM1} -\ ref {COM4}).
Припустимо, три точкові маси розміщуються в\(xy\) -площині наступним чином (припустимо, координати задані в метрах):
- \(m_1=2\,kg\)розміщений на\((−1,3),\)
- \(m_2=6\,kg\)розміщений на\((1,1),\)
- \(m_3=4\,kg\)розміщений на\((2,−2).\)
Знайдіть центр маси системи.
Рішення
Спочатку обчислюємо загальну масу системи:
\[m=\sum_{i=1}^3m_i=2+6+4=12\,kg. \nonumber \]
Далі ми знаходимо моменти щодо\(x\) - і\(y\) -осей:
\[\begin{align*} M_y &=\sum_{i=1}^3m_ix_i=−2+6+8=12, \\[4pt] M_x &=\sum_{i=1}^3m_iy_i=6+6−8=4. \end{align*}\]
Тоді у нас є
\[\bar{x}=\dfrac{M_y}{m}=\dfrac{12}{12}=1 \nonumber \]
і
\[\bar{y}=\dfrac{M_x}{m}=\dfrac{4}{12}=\dfrac{1}{3}. \nonumber \]
Центр маси системи знаходиться\((1,1/3),\) в метрах.
Припустимо, три точкові маси розміщуються на числовій лінії наступним чином (припустимо, координати задані в метрах):
- \(m_1=5\,kg,\)розміщений на\((−2,−3),\)
- \(m_2=3\, kg,\)розміщений на\((2,3),\)
- \(m_3=2\, kg,\)розміщений на\((−3,−2).\)
Знайдіть центр маси системи.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
\((−1,−1)\)м
Центр маси тонких пластин
Поки ми розглянули системи точкових мас на прямій і в площині. Тепер, замість того, щоб мати масу системи, зосереджену в дискретних точках, ми хочемо подивитися на системи, в яких маса системи розподіляється безперервно по тонкому аркушу матеріалу. Для наших цілей ми припускаємо, що лист досить тонкий, щоб до нього можна було ставитися так, ніби він двомірний. Такий лист називається ламіном. Далі ми розробляємо прийоми, щоб знайти центр маси пластинки. У цьому розділі ми також припускаємо, що щільність пластинки постійна.
Ламіни часто представлені двовимірною областю в площині. Геометричний центр такої області називається її центроїдом. Оскільки ми припустили, що щільність пластинки постійна, центр маси пластинки залежить тільки від форми відповідної області в площині; від щільності він не залежить. При цьому центр маси пластинки відповідає центроїду окресленої області в площині. Як і в системах точкових мас, нам потрібно знайти загальну масу пластинки, а також моменти ламіни по відношенню до\(x\) - і\(y\) -осей.
Спочатку розглянемо пластинку у формі прямокутника. Нагадаємо, що центр маси пластинки - це точка, де пластинка балансує. Для прямокутника ця точка є горизонтальним і вертикальним центром прямокутника. Виходячи з цього розуміння, зрозуміло, що центр маси прямокутної ламіни - це точка, де перетинаються діагоналі, що є результатом принципу симетрії, і це заявлено тут без доказів.
Якщо область\(R\) симетрична щодо лінії\(l\), то центроїд\(R\) лежить на\(l\).
Перейдемо до більш загальних ламінам. Припустимо, у нас є пластинка, обмежена вище графіком безперервної функції\(f(x)\), нижче\(x\) -віссю, а зліва і справа лініями\(x=a\) і\(x=b\), відповідно, як показано на наступному малюнку.
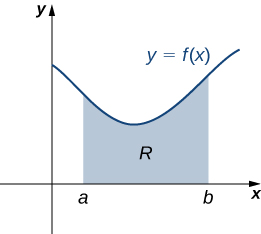
Як і в системах точкових мас, для знаходження центру мас пластинки нам потрібно знайти загальну масу пластинки, а також моменти пластинки по відношенню до\(x\) - і\(y\) -осей. Як ми робили багато разів раніше, ми наближаємо ці величини, розділивши інтервал\([a,b]\) і будуючи прямокутники.
Бо\(i=0,1,2,…,n,\) нехай\(P={x_i}\) буде звичайна перегородка\([a,b]\). Нагадаємо, що ми можемо вибрати будь-яку точку в межах інтервалу\([x_{i−1},x_i]\) як нашу\(x^∗_i\). У цьому випадку ми\(x^∗_i\) хочемо бути x -координатою центроїда наших прямокутників. Таким чином, для\(i=1,2,…,n\), ми вибираємо\(x^∗_i∈[x_{i−1},x_i]\) таку, що\(x^∗_i\) є середньою точкою інтервалу. Тобто,\(x^∗_i=(x_{i−1}+x_i)/2\). Тепер для\(i=1,2,…,n,\) побудови прямокутника висоти\(f(x^∗_i)\)\([x_{i−1},x_i].\) на Центр маси цього прямокутника,\((x^∗_i,(f(x^∗_i))/2),\) як показано на наступному малюнку.
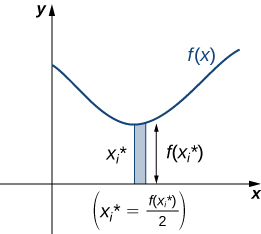
Далі нам потрібно знайти загальну масу прямокутника. \(ρ\)Дозволяти представляти щільність пластинки (зверніть увагу, що\(ρ\) є постійною). При цьому\(ρ\) виражається в перерахунку на масу на одиницю площі. Таким чином, щоб знайти загальну масу прямокутника, помножимо площу прямокутника на\(ρ\). Потім маса прямокутника задається по\(ρf(x^∗_i)Δx\).
Щоб отримати приблизну масу пластинки, складаємо маси всіх прямокутників, щоб вийшло
\[m≈\sum_{i=1}^nρf(x^∗_i)Δx. \label{eq51} \]
Рівняння\ ref {eq51} є сумою Рімана. Беручи межу, як\(n→∞\) дає точну масу пластинки:
\[ \begin{align*} m &=\lim_{n→∞}\sum_{i=1}^nρf(x^∗_i)Δx \\[4pt] &=ρ∫^b_af(x)dx. \end{align*}\]
Далі обчислюємо момент пластинки по відношенню до осі х. Повертаючись до представницького прямокутника, згадаємо його центр мас\((x^∗_i,(f(x^∗_i))/2)\). Нагадаємо також, що трактування прямокутника так, ніби це точкова маса, розташована в центрі маси, не змінює моменту. Таким чином, момент прямокутника щодо осі х задається масою прямокутника\(ρf(x^∗_i)Δx\), помноженої на відстань від центру мас до осі х:\((f(x^∗_i))/2\). Тому момент щодо осі х прямокутника\(ρ([f(x^∗_i)]^2/2)Δx.\) складаємо моменти прямокутників і приймаючи межу одержуваної суми Рімана, бачимо, що момент ламіни по відношенню до осі х дорівнює
\[ \begin{align*}M_x &=\lim_{n→∞}\sum_{i=1}^nρ\dfrac{[f(x^∗_i)]^2}{2}Δx \\[4pt] &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx.\end{align*}\]
Виводимо момент щодо осі y аналогічно, зазначивши, що відстань від центру мас прямокутника до осі y дорівнює\(x^∗_i\). Тоді момент пластинки по відношенню до осі y задається
\[ \begin{align*}M_y &=\lim_{n→∞}\sum_{i=1}^nρx^∗_if(x^∗)i)Δx\\[4pt] &=ρ∫^b_axf(x)dx.\end{align*}\]
Знаходимо координати центру мас шляхом ділення моментів на загальну масу, щоб дати\(\bar{x}=M_y/m\) і\(\bar{y}=M_x/m\). Якщо ми уважно подивимося на вирази для\(M_x,M_y\), і\(m\), ми помічаємо, що константа\(ρ\) скасовує, коли\(\bar{x}\) і\(\bar{y}\) обчислюються.
Ми узагальнюємо ці висновки в наступній теоремі.
Нехай R позначає область, обмежену вище графіком безперервної функції\(f(x)\), нижче - віссю x, а зліва і справа лініями\(x=a\) і\(x=b\) відповідно. Нехай\(ρ\) позначимо щільність пов'язаної з нею пластинки. Тоді ми можемо зробити такі твердження:
- Маса пластинки становить\[m=ρ∫^b_af(x)dx. \label{eq4a} \]
- Моменти\(M_x\) і\(M_y\) ламіни по відношенню до осей x - і y -відповідно є\[M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx\label{eq4b} \] і\[M_y=ρ∫^b_axf(x)dx.\label{eq4c} \]
- Координати центру мас\((\bar{x},\bar{y})\) є\[\bar{x}=\dfrac{M_y}{m} \label{eq4d} \] і\[\bar{y}=\dfrac{M_x}{m}. \label{eq4e} \]
У наступному прикладі ми використовуємо цю теорему, щоб знайти центр маси пластинки.
Нехай R - область, обмежена вище графіком функції\(f(x)=\sqrt{x}\) і нижче по осі x через інтервал\([0,4]\). Знайдіть центроїд області.
Рішення
Регіон зображений на наступному малюнку.
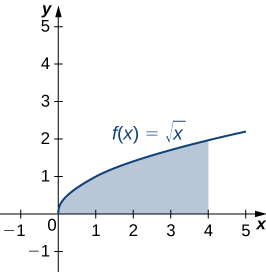
Оскільки нас просять лише центроїд області, а не масу або моменти пов'язаної пламіни, ми знаємо, що постійна щільності\(ρ\) скасовується з розрахунків в кінцевому підсумку. Тому заради зручності припустимо\(ρ=1\).
Для початку нам потрібно обчислити загальну масу (Equation\ ref {eq4a}):
\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^4_0\sqrt{x}dx \\[4pt] &=\dfrac{2}{3}x^{3/2}∣^4_0 \\[4pt] &=\dfrac{2}{3}[8−0] \\[4pt] &=\dfrac{16}{3}. \end{align*}\]
Далі обчислюємо моменти (Рівняння\ ref {eq4d}):
\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=∫^4_0\dfrac{x}{2}dx \\[4pt] &=\dfrac{1}{4}x^2∣^4_0 \\[4pt] &=4 \end{align*}\]
і (Рівняння\ ref {eq4c}):
\[ \begin{align*} M_y &=ρ∫^b_axf(x)dx \\[4pt] &=∫^4_0x\sqrt{x}dx \\[4pt] &=∫^4_0x^{3/2}dx \\[4pt] &=\dfrac{2}{5}x^{5/2}∣^4_0 \\[4pt] &=\dfrac{2}{5}[32−0] \\[4pt] &=\dfrac{64}{5}. \end{align*}\]
Таким чином, ми маємо (Рівняння\ ref {eq4d}):
\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m} \\[4pt] &=\dfrac{64/5}{16/3} \\[4pt] &=\dfrac{64}{5}⋅\dfrac{3}{16} \\[4pt] &=\dfrac{12}{5} \end{align*}\]
і (Рівняння\ ref {eq4e}):
\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y} \\[4pt] &=\dfrac{4}{16/3} \\[4pt] &=4⋅\dfrac{3}{16} \\[4pt] &=\dfrac{3}{4}. \end{align*}\]
Центроїд області - це\((12/5,3/4).\)
\(R\)Дозволяти область обмежена вище графіком функції\(f(x)=x^2\) і нижче по осі x через інтервал\([0,2].\) Знайти центроїд області.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
Центроїд області - це\((3/2,6/5).\)
Ми можемо адаптувати цей підхід, щоб знайти центроїди більш складних регіонів. Припустимо, наша область обмежена вище графіком безперервної функції\(f(x)\), як і раніше, але тепер, замість того, щоб нижня межа для області була осі x, припустимо, область обмежена нижче графіком другої безперервної функції\(g(x)\), як показано на малюнку\(\PageIndex{7}\).
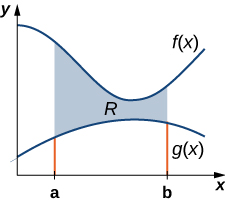
Знову поділяємо інтервал\([a,b]\) і будуємо прямокутники. Представницький прямокутник зображений на малюнку\(\PageIndex{8}\).
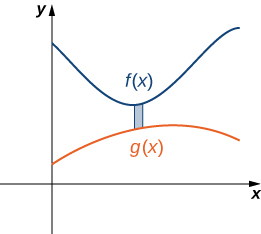
Зверніть увагу, що центроїд цього прямокутника є\((x^∗_i,(f(x^∗_i)+g(x^∗_i))/2)\). Ми не будемо розглядати всі деталі розробки суми Рімана, але давайте розглянемо деякі ключові кроки. При розробці формул для маси пластинки і моменту щодо осі y задається висота кожного прямокутника\(f(x^∗_i)−g(x^∗_i)\), що призводить до виразу\(f(x)−g(x)\) в integrands.
При розробці формули для моменту щодо осі х момент кожного прямокутника знаходять множенням площі прямокутника,\(ρ[f(x^∗_i)−g(x^∗_i)]Δx,\) на відстань центроїда від\(x\) -осі\((f(x^∗_i)+g(x^∗_i))/2\), що дає\(ρ(1/2){[f(x^∗_i)]^2−[g(x^∗_i)]^2}Δx\). Підсумовуючи ці висновки, ми дійдемо до наступної теореми.
\(R\)Позначимо область, обмежену вище графіком безперервної функції\(f(x),\) нижче графіком неперервної функції\(g(x)\), а зліва і справа - лініями\(x=a\) і\(x=b\) відповідно. Нехай\(ρ\) позначимо щільність пов'язаної з нею пластинки. Тоді ми можемо зробити такі твердження:
- Маса пластинки становить\[m=ρ∫^b_a[f(x)−g(x)]dx. \nonumber \]
- Моменти\(M_x\) і\(M_y\) пластинки по відношенню до осей х і у відповідно є\[M_x=ρ∫^b_a12([f(x)]^2−[g(x)]^2)dx \nonumber \] і\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
- Координати центру мас\(\bar{x},\bar{y})\) є\[\bar{x}=\dfrac{M_y}{m} \nonumber \] і\[\bar{y}=\dfrac{M_x}{m} \nonumber \]
Ми проілюструємо цю теорему в наступному прикладі.
Нехай R - область, обмежена вище графіком функції\(f(x)=1−x^2\) і нижче графіком функції\(g(x)=x−1.\) Знайти центроїд області.
Рішення
Регіон зображений на наступному малюнку.
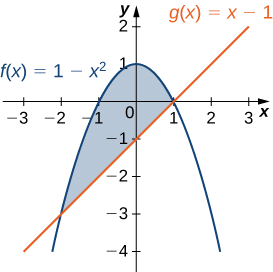
Графіки функцій перетинаються в\((−2,−3)\) і\((1,0)\), тому ми інтегруємо від −2 до 1. Ще раз, заради зручності, припустимо\(ρ=1\).
Для початку нам потрібно розрахувати загальну масу:
\[ \begin{align*} m &=ρ∫^b_a[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}[1−x^2−(x−1)]dx \\[4pt] &=∫^1_{−2}(2−x^2−x)dx \\[4pt] &=\left[2x−\dfrac{1}{3}x^3−\dfrac{1}{2}x^2\right]∣^1_{−2} \\[4pt] &=\left[2−\dfrac{1}{3}−\dfrac{1}{2}\right]−\left[−4+\dfrac{8}{3}−2\right]\\[4pt] &=\dfrac{9}{2}. \end{align*}\]
Далі обчислюємо моменти:
\[ \begin{align*} M_x&=ρ∫^b_a\dfrac{1}{2}([f(x)]^2−[g(x)]^2)dx \\[4pt] &=\dfrac{1}{2}∫^1_{−2}((1−x^2)^2−(x−1)^2)dx\\[4pt] &=\dfrac{1}{2}∫^1_{−2}(x^4−3x^2+2x)dx \\[4pt] &=\dfrac{1}{2} \left[\dfrac{x^5}{5}−x^3+x^2\right]∣^1_{−2}\\[4pt] &=−\dfrac{27}{10} \end{align*}\]
і
\[ \begin{align*} M_y &=ρ∫^b_ax[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}x[(1−x^2)−(x−1)]dx\\[4pt] &=∫^1_{−2}x[2−x^2−x]dx\\[4pt] &=∫^1_{−2}(2x−x^4−x^2)dx \\[4pt] &=\left[x^2−\dfrac{x^5}{5}−\dfrac{x^3}{3}\right]∣^1_{−2}\\[4pt] &=−\dfrac{9}{4}. \end{align*}\]
Тому у нас є
\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m}\\[4pt] &=−\dfrac{9}{4}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{1}{2} \end{align*}\]
і
\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y}\\[4pt] &=−\dfrac{27}{10}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{3}{5}. \end{align*}\]
Центроїд області - це\((−(1/2),−(3/5)).\)
\(R\)Дозволяти область, обмежена вище графіком функції\(f(x)=6−x^2\) і нижче графіком функції\(g(x)=3−2x.\) Знайти центроїд області.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
Центроїд області - це\((1,13/5).\)
Принцип симетрії
Принцип симетрії ми заявляли раніше, коли дивилися на центроїд прямокутника. Принцип симетрії може стати великою підмогою при знаходженні центроїдів областей, які є симетричними. Розглянемо наступний приклад.
Нехай R - область, обмежена вище графіком функції\(f(x)=4−x^2\) і нижче по осі x. Знайдіть центроїд області.
Рішення
Регіон зображений на наступному малюнку
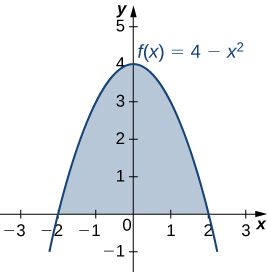
Область симетрична по відношенню до осі y. Тому x-координата центроїда дорівнює нулю. Нам потрібно тільки розрахувати\(\bar{y}\). Ще раз, заради зручності, припустимо\(ρ=1\).
Спочатку розрахуємо загальну масу:
\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^2_{−2}(4−x^2)dx \\[4pt] &=\left[4x−\dfrac{x^3}{3}\right]∣^2_{−2} \\[4pt] &=\dfrac{32}{3}. \end{align*}\]
Далі обчислюємо моменти. Нам знадобляться тільки\(M_x\):
\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=\dfrac{1}{2}∫^2_{−2}\left[4−x^2\right]^2dx =\dfrac{1}{2}∫^2_{−2}(16−8x^2+x^4)dx \\[4pt] &=\dfrac{1}{2}\left[\dfrac{x^5}{5}−\dfrac{8x^3}{3}+16x\right]∣^2_{−2}=\dfrac{256}{15} \end{align*}\]
Тоді у нас є
\[\bar{y}=\dfrac{M_x}{y}=\dfrac{256}{15}⋅\dfrac{3}{32}=\dfrac{8}{5}. \nonumber \]
Центроїд області - це\((0,8/5).\)
\(R\)Дозволяти область обмежена вище графіком функції\(f(x)=1−x^2\) і нижче по\(x\) -осі. Знайдіть центроїд області.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
Центроїд області - це\((0,2/5).\)
Великий каньйон Skywalk відкрився для публіки 28 березня 2007 року. Це інженерне диво - це оглядовий майданчик у формі підкови, підвішений на 4000 футів над річкою Колорадо на західному краю Гранд-Каньйону. Його кришталево чиста скляна підлога дозволяє приголомшливий вид на каньйон внизу (див. Наступний малюнок).

Skywalk - це консольна конструкція, що означає, що оглядовий майданчик простягається над ободом каньйону, без видимих засобів підтримки під ним. Незважаючи на відсутність видимих опорних стійок або підкосів, консольні конструкції сконструйовані так, щоб бути дуже стійкими, і Skywalk не є винятком. Оглядовий майданчик міцно прикріплений до опорних стовпів, які простягаються на 46 футів вниз в корінну скелю. Структура була побудована, щоб протистояти вітрам 100 миль/год і землетрусу магнітудою 8,0 в межах 50 миль, і здатна підтримувати понад 70 000 000 фунтів.
Одним з факторів, що впливають на стійкість Skywalk, є центр ваги конструкції. Ми розрахуємо центр ваги Skywalk, і вивчимо, як змінюється центр ваги, коли туристи виходять на оглядовий майданчик.
Оглядовий майданчик має П-подібну форму. Ноги U мають ширину 10 футів і починаються на суші, під центром відвідувачів, 48 футів від краю каньйону. Платформа простягається на 70 футів над краєм каньйону.
Щоб обчислити центр мас конструкції, розглядаємо її як пластинку і використовуємо двовимірну область в xy-площині для представлення платформи. Ми починаємо з поділу регіону на три субрегіони, щоб ми могли розглянути кожен субрегіон окремо. Перша область, позначена\(R_1\), складається з вигнутої частини U. моделюємо у\(R_1\) вигляді напівкруглого кільця, з внутрішнім радіусом 25 футів і зовнішнім радіусом 35 футів, центрованим у початку (рис.\(\PageIndex{12}\)).
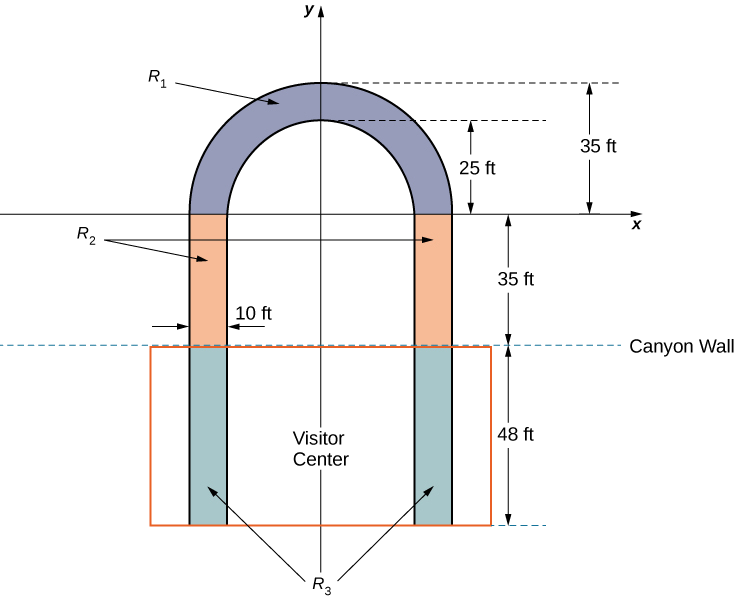
Ноги платформи, що простягаються 35 футів між\(R_1\) стіною каньйону, складають другий субрегіон,\(R_2\). Останній, кінці ніг, які простягаються 48 футів під центром відвідувачів, складають третій субрегіон,\(R_3\). Припустимо, що щільність пламіни постійна і припустимо, що загальна вага платформи становить 1 200 000 фунтів (не враховуючи вагу центру відвідувачів; ми розглянемо це пізніше). Використовувати\(g=32\;ft/sec^2\).
- Обчислити площу кожної з трьох підобластей. Зверніть увагу, що області областей\(R_2\) і\(R_3\) повинні включати тільки області ніг, а не відкритий простір між ними. Круглі відповіді на найближчий квадратний фут.
- Визначте масу, пов'язану з кожним з трьох підобластей.
- Обчисліть центр маси кожної з трьох підобластей.
- Тепер розглядайте кожну з трьох підобластей як точкову масу, розташовану в центрі маси відповідної субобласті. Використовуючи це уявлення, обчислити центр маси всієї платформи.
- Припустимо, що центр відвідувачів важить 2,200,000 фунтів, з центром маси, відповідним центру\(R_3\) маси з.Трактування центру відвідувачів як точкової маси, перерахуйте центр маси системи. Як змінюється центр маси?
- Хоча Skywalk був побудований для обмеження кількості людей на оглядовому майданчику до 120, платформа здатна підтримувати до 800 осіб вагою 200 фунтів кожен. Якби всі 800 чоловік були допущені на платформу, і всі вони пішли в найдальший кінець платформи, як би вплинув на центр ваги системи? (Включіть центр відвідувачів у розрахунки та представляйте людей точковою масою, розташованою на найдальшому краю платформи, 70 футів від стіни каньйону.)
Теорема Паппуса
Цей розділ закінчується обговоренням теореми Паппуса за об'ємом, яка дозволяє знайти обсяг конкретних видів твердих тіл за допомогою центроїда. (Існує також теорема Паппуса для площі поверхні, але вона набагато менш корисна, ніж теорема про обсяг.)
\(R\)Дозволяти область в площині і нехай l бути лінія в площині, яка не перетинається\(R\). Тоді обсяг твердого тіла обертання, утвореного\(R\) обертанням навколо l, дорівнює площі,\(R\) помноженої на відстань d, пройдену центроїдом\(R\).
Ми можемо довести випадок, коли область обмежена вище графіком функції,\(f(x)\) а нижче - графіком функції\(g(x)\) через інтервал\([a,b]\), і для якої віссю обертання є\(y\) -вісь. В даному випадку площа області - це\(\displaystyle A=∫^b_a[f(x)−g(x)]\,dx\). Оскільки віссю обертання є\(y\) -вісь, то відстань, пройдене центроїдом області, залежить тільки від\(x\) -координати центроїда\(\bar{x}\), яка
\[x=\dfrac{M_y}{m}, \nonumber \]
де
\[m=ρ∫^b_a[f(x)−g(x)]dx \nonumber \]
і
\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Потім,
\[d=2π\dfrac{\displaystyle {ρ∫^b_ax[f(x)−g(x)]dx}}{\displaystyle{ρ∫^b_a[f(x)−g(x)]dx}} \nonumber \]
і таким чином
\[d⋅A=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Однак, використовуючи метод циліндричних оболонок, ми маємо
\[V=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Отже,
\[V=d⋅A \nonumber \]
і доказ є повним.
□
\(R\)Дозволяти коло радіуса 2 по центру\((4,0).\) Використовуйте теорему Паппуса для об'єму, щоб знайти об'єм тора, породженого обертанням\(R\) навколо\(y\) -осі.
Рішення
Область і тор зображені на наступному малюнку.
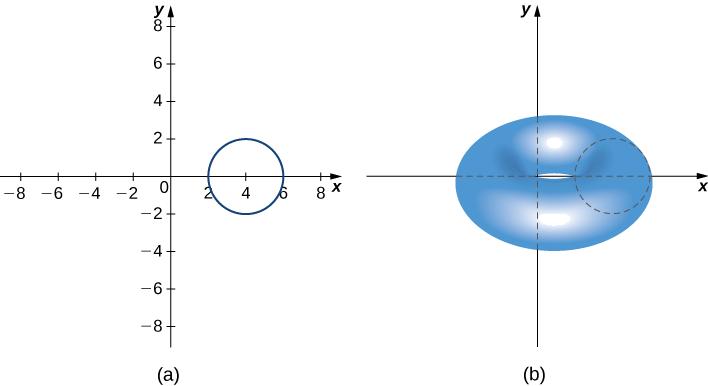
Область\(R\) - це коло радіусом 2, тому площа R дорівнює\(A=4π\;\text{units}^2\). За принципом симетрії центроїд R є центром кола. Центроїд рухається навколо\(y\) -осі по круговому шляху радіусом 4, тому центроїд подорожує\(d=8π\) одиницями. Тоді обсяг тора дорівнює\(A⋅d=32π^2\) одиницям 3.
Нехай R - коло радіуса 1 по центру\((3,0).\) Використовуйте теорему Паппуса для об'єму, щоб знайти об'єм тора, породженого обертанням R навколо\(y\) осі.
- Підказка
-
Скористайтеся процесом з попереднього прикладу.
- Відповідь
-
\(6π^2\)одиниць 3
Ключові концепції
- Математично центр маси системи - це точка, в якій загальна маса системи може бути зосереджена без зміни моменту. Вільно кажучи, центр маси можна розглядати як точку балансування системи.
- Для точкових мас, розподілених по числовій лінії, момент системи щодо початку є\(\displaystyle M=\sum^n_{i=1}m_ix_i.\) Для точкових мас, розподілених в площині, моменти системи щодо\(x\) - і\(y\) -осей відповідно є\(\displaystyle M_x=\sum^n_{i=1}m_iy_i\) і\(\displaystyle M_y=\sum^n_{i=}m_ix_i\) відповідно.
- Для ламіни, обмеженої вище функцією\(f(x)\), моменти системи щодо\(x\) - і\(y\) -осей, відповідно, є\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) і\(\displaystyle M_y=ρ∫^b_axf(x)\,dx.\)
- \(x\)- і\(y\) -координати центру мас можна знайти, розділивши моменти навколо\(y\) -осі і навколо\(x\) -осі відповідно на загальну масу. Принцип симетрії говорить, що якщо область симетрична по відношенню до лінії, то центроїд області лежить на лінії.
- Теорема Паппуса для обсягу говорить, що якщо область обертається навколо зовнішньої осі, обсяг отриманого твердого тіла дорівнює площі області, помноженої на відстань, пройдену центроїдом області.
Ключові рівняння
- Маса пластинки
\(\displaystyle m=ρ∫^b_af(x)dx\)
- Моменти ламіни
\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\text{ and }M_y=ρ∫^b_axf(x)\,dx\)
- Центр маси пластинки
\(\bar{x}=\dfrac{M_y}{m}\text{ and }\bar{y}=\dfrac{M_x}{m}\)
Глосарій
- центр маси
- точка, в якій можна було б сконцентрувати загальну масу системи, не змінюючи момент
- центроїд
- центроїд області - геометричний центр області; пламіни часто представлені областями в площині; якщо пластинка має постійну щільність, центр маси пластинки залежить тільки від форми відповідної плоской області; в цьому випадку центр маси пластинки відповідає центроїд представницького регіону
- ламіна
- тонкий лист матеріалу; ламіни досить тонкі, що в математичних цілях вони можуть розглядатися так, ніби вони двовимірні
- момент
- якщо n мас розташовані на числовій лінії, то момент системи щодо початку заданий\(\displaystyle M=\sum^n_{i=1}m_ix_i\); якщо замість цього розглядати область в площині, обмежену вище функцією\(f(x)\) через інтервал\([a,b]\), то моменти області по відношенню до\(x\) - і \(y\)-осі задаються\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) і\(\displaystyle M_y=ρ∫^b_axf(x)\,dx\), відповідно
- принцип симетрії
- принцип симетрії стверджує, що якщо область\(R\) симетрична навколо лінії\(I\), то центроїд\(R\) лежить на\(I\)
- теорема Паппуса для обсягу
- ця теорема стверджує, що обсяг твердого тіла обертання, утвореного обертанням області навколо зовнішньої осі, дорівнює площі області, помноженої на відстань, пройдену центроїдом області
