6.5: Фізичні програми інтеграції

Цілі навчання

• Визначте масу одновимірного об'єкта за його лінійною функцією щільності.
• Визначте масу двовимірного кругового об'єкта за його радіальною функцією щільності.
• Обчисліть виконану роботу змінною силою, що діє уздовж лінії.
• Розрахуйте роботу, виконану при перекачуванні рідини з однієї висоти на іншу.
• Знайдіть гідростатичну силу проти зануреної вертикальної пластини.

У цьому розділі ми розглянемо деякі фізичні програми інтеграції. Почнемо з розрахунку маси з функції щільності. Потім звертаємо свою увагу на роботу, і закриваємо ділянку з вивченням гідростатичної сили.

Маса і щільність

Ми можемо використовувати інтеграцію для розробки формули розрахунку маси на основі функції щільності. Спочатку розглянемо тонкий стрижень або дріт. Орієнтуйте стрижень так, щоб він вирівнявся з$x$ -віссю, з лівим кінцем стрижня на$x=a$ і правим кінцем стрижня на$x=b$ (рис.$\PageIndex{1}$). Зверніть увагу, що хоча ми зображуємо стрижень з деякою товщиною на малюнках, для математичних цілей ми припускаємо, що стрижень досить тонкий, щоб його розглядали як одновимірний об'єкт.

Малюнок$\PageIndex{1}$: Ми можемо обчислити масу тонкого стрижня, орієнтованого вздовж$x$ -осі, інтегруючи його функцію щільності.

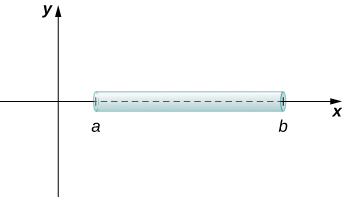
Якщо стрижень має постійну щільність$ρ$, наведену в перерахунку на масу на одиницю довжини, то маса стрижня - це всього лише твір щільності і довжини стрижня:$(b−a)ρ$. Однак, якщо щільність стрижня не постійна, проблема стає трохи складнішою. Коли щільність стрижня змінюється від точки до точки, ми використовуємо функцію лінійної щільності$ρ(x)$, для позначення щільності стрижня в будь-якій точці,$x$. $ρ(x)$Дозволяти інтегрується лінійна функція щільності. Тепер, для$i=0,1,2,…,n$ нехай$P={x_i}$ буде регулярний поділ інтервалу$[a,b]$, а для$i=1,2,…,n$ вибрати довільну точку$x^∗_i∈[x_{i−1},x_i]$. $\PageIndex{2}$На малюнку зображений представницький сегмент вудилища.

Малюнок$\PageIndex{2}$: Представницький сегмент стрижня.

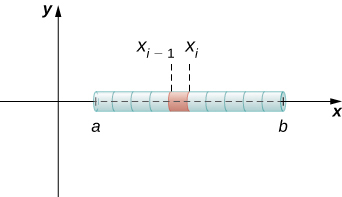
Маса$m_i$ відрізка стрижня від$x_{i−1}$ до$x_i$ наближена

$$\begin{align*} m_i ≈ρ(x^∗_i)(x_i−x_{i−1}) \\[4pt] =ρ(x^∗_i)Δx. \end{align*} \nonumber$$

Додавання мас всіх сегментів дає нам наближення для маси всього стрижня:

$$\begin{align*} m =\sum_{i=1}^nm_i \\[4pt] ≈\sum_{i=1}^nρ(x^∗_i)Δx. \end{align*} \nonumber$$

Це сума Рімана. Взявши межу як$n→∞$, отримаємо вираз для точної маси стрижня:

$$\begin{align*} m =\lim_{n→∞}\sum_{i=1}^nρ(x^∗_i)Δx \\[4pt] =\int ^b_aρ(x)dx. \end{align*} \nonumber$$

Цей результат ми констатуємо в наступній теоремі.

Формула маси — щільності одновимірного об'єкта

З огляду на тонкий стрижень, орієнтований уздовж$x$ -осі над інтервалом$[a,b]$, нехай$ρ(x)$ позначимо лінійну функцію щільності, що дає щільність стрижня$x$ в точці інтервалу. Потім маса стрижня задається

$$m=\int ^b_aρ(x)dx. \label{density1}$$

Ми застосуємо цю теорему в наступному прикладі.

Приклад$\PageIndex{1}$: Calculating Mass from Linear Density

Розглянемо тонкий стрижень, орієнтований на$x$ -осі через інтервал$[π/2,π]$. Якщо щільність стрижня задана$ρ(x)=\sin x$, яка маса стрижня?

Рішення

Застосовуючи рівняння\ ref {density1} безпосередньо, ми маємо

$$\begin{align*} m =\int ^b_aρ(x)dx \nonumber \\[4pt] = \int ^π_{π/2}\sin x \,dx \nonumber \\[4pt] = −\cos x \Big|^π_{π/2} \nonumber \\[4pt] = 1. \nonumber \end{align*}$$

Вправа$\PageIndex{1}$

Розглянемо тонкий стрижень, орієнтований на$x$ -осі через інтервал$[1,3]$. Якщо щільність стрижня задається$ρ(x)=2x^2+3,$ тим, яка маса стрижня?

Підказка

Скористайтеся процесом з попереднього прикладу.

Рішення

$70/3$

Тепер ми розширимо цю концепцію, щоб знайти масу двовимірного радіусного диска$r$. Як і зі стрижнем, який ми розглядали в одновимірному випадку, тут ми припускаємо, що диск досить тонкий, щоб в математичних цілях ми могли розглядати його як двовимірний об'єкт. Ми припускаємо, що щільність задана через масу на одиницю площі (називається щільністю площі), і далі припустимо, що щільність змінюється тільки по радіусу диска (називається радіальною щільністю). Орієнтуємо диск в$xy-plane$, з центром у початку. Потім щільність диска може розглядатися як функція$x$, позначається$ρ(x)$. Ми припускаємо$ρ(x)$, що інтегрується. Оскільки щільність є функцією$x$, ми розділимо інтервал від$[0,r]$ вздовж$x$ -осі. Для$i=0,1,2,…,n$, нехай$P={x_i}$ буде регулярний поділ інтервалу$[0,r]$, а для$i=1,2,…,n$, вибираємо довільну точку$x^∗_i∈[x_{i−1},x_i]$. Тепер за допомогою розділу розбийте диск на тонкі (двовимірні) шайби. Диск і представницька шайба зображені на наступному малюнку.

Малюнок$\PageIndex{3}$: (а) Тонкий диск у xy -площині. (б) представницька шайба.

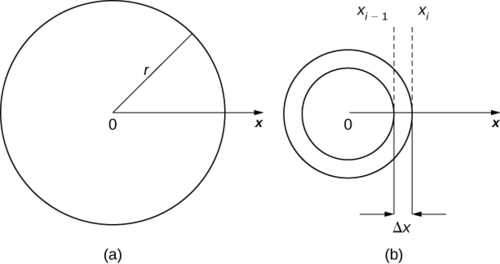
Тепер ми наближаємо щільність і площу шайби, щоб розрахувати приблизну масу,$m_i$. Зверніть увагу, що площа шайби задається

$$\begin{align*} A_i =π(x_i)^2−π(x_{i−1})^2 \\[4pt] =π[x^2_i−x^2_{i−1}] \\[4pt] =π(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =π(x_i+x_{i−1})Δx. \end{align*}$$

Ви можете згадати, що у нас був вираз, подібний до цього, коли ми обчислювали обсяги оболонками. Як ми там робили, використовуємо$x^∗_i≈(x_i+x_{i−1})/2$ для наближення середній радіус шайби. Отримуємо

$$A_i=π(x_i+x_{i−1})Δx≈2πx^∗_iΔx. \nonumber$$

Використовуючи$ρ(x^∗_i)$ для наближення щільності шайби, наближаємо масу шайби на

$$m_i≈2πx^∗_iρ(x^∗_i)Δx. \nonumber$$

Складаючи маси шайб, ми бачимо, що маса$m$ всього диска наближена

$$m=\sum_{i=1}^nm_i≈\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx. \nonumber$$

Ми знову визнаємо це як суму Рімана, і беремо межу, як$n→∞.$ Це дає нам

$$\begin{align*} m =\lim_{n→∞}\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx \\[4pt] =\int ^r_02πxρ(x)dx. \end{align*}$$

Ми узагальнюємо ці висновки в наступній теоремі.

Формула маси — щільності кругового об'єкта

$ρ(x)$Дозволяти інтегрується функція, що представляє радіальну щільність диска радіуса$r$. Потім маса диска задається

$$m=\int ^r_02πxρ(x)dx. \label{massEq1}$$

Приклад$\PageIndex{2}$: Calculating Mass from Radial Density

$ρ(x)=\sqrt{x}$Дозволяти представляти радіальну щільність диска. Обчисліть масу диска радіусом 4.

Рішення

Застосовуючи рівняння\ ref {MasseQ1}, знаходимо

$$\begin{align*} m =\int ^r_02πxρ(x)dx \nonumber \\[4pt] =\int ^4_02πx\sqrt{x}dx=2π\int ^4_0x^{3/2}dx \nonumber \\[4pt] =2π\dfrac{2}{5}x^{5/2}∣^4_0=\dfrac{4π}{5}[32] \nonumber \\[4pt] =\dfrac{128π}{5}.\nonumber \end{align*}$$

Вправа$\PageIndex{2}$

$ρ(x)=3x+2$Дозволяти представляти радіальну щільність диска. Обчисліть масу диска радіусом 2.

Підказка

Скористайтеся процесом з попереднього прикладу.

Рішення

$24π$

Робота, виконана силою

Ми зараз розглянемо роботу. У фізиці робота пов'язана з силою, яка часто інтуїтивно визначається як поштовх або тяга на предмет. Коли сила рухає об'єкт, ми говоримо, що сила працює над об'єктом. Іншими словами, робота може розглядатися як кількість енергії, необхідної для переміщення об'єкта. Згідно з фізикою, коли ми маємо постійну силу, робота може виражатися як добуток сили і відстані.

В англійській системі одиницею сили є фунт, а одиницею відстані є стопа, тому робота дається в фут-фунтах. У метричній системі використовуються кілограми і метри. Один ньютон - сила, необхідна для прискорення$1$ кілограма маси зі швидкістю$1$ м/сек ². Таким чином, найпоширенішою одиницею роботи є ньютон-метр. Цю ж одиницю ще називають джоулем. Обидва визначаються як кілограми разів метрів в квадраті за секунди в квадраті$(kg⋅m^2/s^2).$

Коли ми маємо постійну силу, справи йдуть досить легко. Однак рідко, щоб сила була постійною. Наприклад, робота, виконана для стиснення (або подовження) пружини, змінюється залежно від того, наскільки пружина вже була стиснута (або розтягнута). Більш детально ми розглянемо пружини далі в цьому розділі.

Припустимо, у нас є змінна сила$F(x)$, яка рухає об'єкт у позитивному напрямку вздовж$x$ -осі від точки$a$ до точки$b$. Щоб розрахувати виконану роботу, розділимо інтервал$[a,b]$ і оцінюємо виконану роботу по кожному підінтервалу. Отже, для$i=0,1,2,…,n$, нехай$P={x_i}$ буде регулярний поділ інтервалу$[a,b]$, а для$i=1,2,…,n$, вибираємо довільну точку$x^∗_i∈[x_{i−1},x_i]$. Щоб обчислити виконану роботу по переміщенню об'єкта з точки$x_{i−1}$ в точку$x_i$, ми припускаємо, що сила приблизно постійна протягом інтервалу, і використовуємо$F(x^∗_i)$ для наближення сили. Робота, виконана за інтервал$[x_{i−1},x_i]$, то, дається

$$W_i≈F(x^∗_i)(x_{i}−x_{i−1})=F(x^∗_i)Δx. \nonumber$$

Тому робота, виконана за інтервал$[a,b]$, приблизно

$$W=\sum_{i=1}^nW_i≈\sum_{i=1}^nF(x^∗_i)Δx. \nonumber$$

Беручи межу цього виразу як$n→∞$ дає нам точне значення для роботи:

$$\begin{align*} W =\lim_{n→∞}\sum_{i=1}^nF(x^∗_i)Δx \\[4pt] =\int ^b_aF(x)dx. \end{align*}$$

Таким чином, ми можемо визначити роботу наступним чином.

Визначення: Робота

Якщо змінна сила$F(x)$ переміщує об'єкт у позитивному напрямку вздовж$x$ -осі з точки$a$ в точку$b$, то робота, виконана над об'єктом, є

$$W=\int ^b_aF(x)dx. \label{work}$$

Зверніть увагу,$F$ що якщо константа, то інтеграл оцінює, до$F⋅(b−a)=F⋅d,$ якої є формула, яку ми виклали на початку цього розділу.

Тепер давайте розглянемо конкретний приклад виконаної роботи по стисненню або подовженню пружини. Розглянемо блок, прикріплений до горизонтальної пружини. Блок рухається вперед-назад, коли пружина розтягується і стискається. Хоча в реальному світі нам довелося б враховувати силу тертя між блоком і поверхнею, на якій він спирається, ми ігноруємо тертя тут і припускаємо, що блок спирається на поверхню без тертя. Коли пружина знаходиться на своїй природній довжині (в спокої), система, як кажуть, знаходиться в рівновазі. У такому стані пружина ні витягнута, ні стискається, і в такому положенні рівноваги блок не рухається до тих пір, поки не буде введено деяке зусилля. Орієнтуємо систему таку, яка$x=0$ відповідає положенню рівноваги (рис.$\PageIndex{4}$).

0 і позначений розтягнутим." style="width: 439px; height: 484px;" width="439px" height="484px" src="https://math.libretexts.org/@api/dek...06_05_004.jpeg">

Малюнок$\PageIndex{4}$: Блок, прикріплений до горизонтальної пружини в рівновазі, стиснутий і подовжений.

Відповідно до закону Гука, сила, необхідна для стиснення або розтягування пружини з положення рівноваги, дається$F(x)=kx$, для деякої постійної$k$. Значення k залежить від фізичних характеристик пружини. Константа$k$ називається постійною пружини і завжди позитивна. Ми можемо використовувати цю інформацію для розрахунку виконаної роботи зі стиснення або подовження пружини, як показано в наступному прикладі.

Приклад$\PageIndex{3}$: The Work Required to Stretch or Compress a Spring

Припустимо, для стиснення пружини$0.2$ m з положення рівноваги потрібна сила$10$ N (в негативному напрямку). Скільки проводиться робота по витягуванню пружини$0.5$ m з положення рівноваги?

Рішення

Спочатку знайдіть постійну пружини,$k$. Коли$x=−0.2$, ми$F(x)=−10,$ так знаємо

$$\begin{align*} F(x) =kx \\[4pt] −10 =k(−0.2) \\[4pt] k =50 \end{align*}$$

а$F(x)=50x.$ потім, для розрахунку роботи, інтегруємо силову функцію, отримуючи

$$\begin{align*} W = \int ^b_aF(x)dx \\[4pt] =\int ^{0.5}_050 x \,dx \\[4pt] =\left. 25x^2 \right|^{0.5}_0 \\[4pt] =6.25. \end{align*}$$

Роботу, виконану для розтягування пружини, є$6.25$ Дж.

Вправа$\PageIndex{3}$

Припустимо, що потрібно сила$8$ lb, щоб розтягнути$6$ пружину в. з положення рівноваги. Скільки роботи робиться для розтягування пружини$1$ футів з положення рівноваги?

Підказка

Скористайтеся процесом з попереднього прикладу. Будьте обережні з одиницями.

Рішення

$8$фут-фунт

Робота, виконана в насосі

Розглянемо виконану роботу по відкачуванню води (або якоїсь іншої рідини) з бака. Проблеми з накачуванням трохи складніше, ніж проблеми з пружиною, оскільки багато розрахунків залежать від форми та розміру бака. Крім того, замість того, щоб турбуватися про роботу, виконану для переміщення однієї маси, ми дивимося на роботу, виконану для переміщення об'єму води, і для переміщення води з дна резервуара потрібно більше роботи, ніж для переміщення води з верхньої частини резервуара.

Ми розглядаємо процес в контексті циліндричного резервуара, потім розглянемо пару прикладів з використанням танків різної форми. Припустимо, циліндричний резервуар радіусом$4$$10$ м і висотою м заповнений на глибину 8 м. скільки потрібно роботи, щоб перекачати всю воду через верхній край бака?

Перше, що нам потрібно зробити, це визначити систему відліку. Дозволяємо$x$ представляти вертикальну відстань нижче верхньої частини бака. Тобто ми орієнтуємо$x$ -вісь вертикально, при цьому початок у верхній частині резервуара, а напрямок вниз - позитивним (рис.$\PageIndex{5}$).

Малюнок$\PageIndex{5}$: Скільки потрібно робіт, щоб спорожнити ємність, частково заповнену водою?

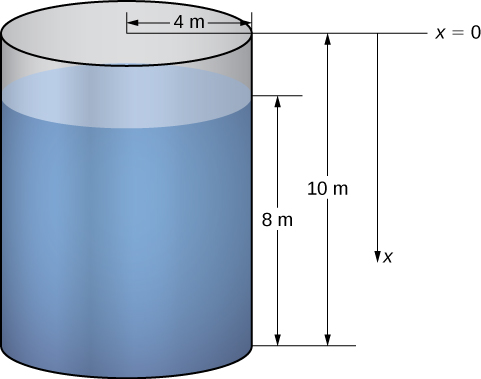
Використовуючи цю систему координат, вода поширюється від$x=2$ до$x=10$. Тому ділимо інтервал$[2,10]$ і дивимося на роботу, необхідну для підняття кожного окремого «шару» води. Отже, для$i=0,1,2,…,n$, нехай$P={x_i}$ буде регулярний поділ інтервалу$[2,10]$, а для$i=1,2,…,n$, вибираємо довільну точку$x^∗_i∈[x_{i−1},x_i]$. На малюнку$\PageIndex{6}$ зображений представницький шар.

Малюнок$\PageIndex{6}$: Представницький шар води.

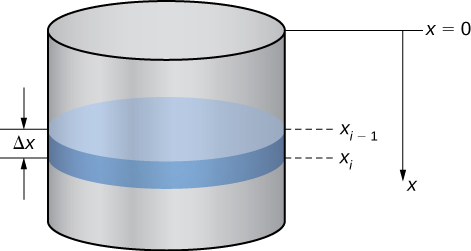
У проблемах з накачуванням сила, необхідна для підйому води до верхньої частини бака, - це сила, необхідна для подолання сили тяжіння, тому вона дорівнює вазі води. З огляду на, що вага-щільність води є$9800 \, \text{N/m}^3$$62.4\,\text{lb/ft}^3$, або, розрахунок обсягу кожного шару дає нам вагу. У цьому випадку ми маємо

$$V=π(4)^2Δx=16πΔx. \nonumber$$

Потім сила, необхідна для підняття кожного шару,

$$F=9800⋅16πΔx=156,800πΔx. \nonumber$$

Зверніть увагу, що цей крок стає трохи складніше, якщо у нас є нециліндричний бак. Ми розглянемо нециліндричний резервуар в наступному прикладі.

Нам також потрібно знати відстань, на яку воду потрібно піднімати. Виходячи з нашого вибору систем координат, ми можемо використовувати$x^∗_i$ як наближення відстані, яку шар повинен бути піднятий. Тоді робота по підняттю$i^{\text{th}}$ шару води$W_i$ йде приблизно

$$W_i≈156,800πx^∗_iΔx. \nonumber$$

Складаючи роботу для кожного шару, ми бачимо приблизну роботу по спустошенню резервуара, яку дає

$$\begin{align*} W =\sum_{i=1}^nW_i \\[4pt] ≈\sum_{i=1}^n156,800πx^∗_iΔx.\end{align*}$$

Це сума Рімана, тому беручи ліміт, як$n→∞,$ ми отримуємо

$$\begin{align*} W =\lim_{n→∞}\sum^n_{i=1}156,800πx^∗_iΔx \\[4pt] = 156,800π\int ^{10}_2xdx \\[4pt] =156,800π \left( \dfrac{x^2}{2}\right)\bigg|^{10}_2=7,526,400π≈23,644,883. \end{align*}$$

Робота, необхідна для спорожнення бака, становить приблизно 23,650 000 Дж.

Для проблем з накачуванням розрахунки варіюються в залежності від форми бака або контейнера. Наступна стратегія вирішення проблем викладає покроковий процес вирішення задач прокачування.

Стратегія вирішення проблем: рішення проблем з накачуванням

1. Намалюйте малюнок танка і виберіть відповідну рамку відліку.
2. Розрахуйте обсяг представницького шару води.
3. Помножте обсяг на вагу-щільність води, щоб отримати силу.
4. Розрахуйте відстань, на яку повинен бути піднятий шар води.
5. Помножте силу і відстань, щоб отримати оцінку роботи, необхідної для підняття шару води.
6. Підсумуйте роботу, необхідну для підняття всіх верств. Цей вислів є оцінкою роботи, необхідної для відкачування потрібної кількості води, і воно у вигляді суми Рімана.
7. Візьміть ліміт як$n→∞$ і оцініть отриманий інтеграл, щоб отримати точну роботу, необхідну для відкачування потрібної кількості води.

Зараз ми застосовуємо цю стратегію вирішення проблем у прикладі з нециліндричним резервуаром.

Приклад$\PageIndex{4}$: A Pumping Problem with a Noncylindrical Tank

Припустимо, резервуар у формі перевернутого конуса, з висотою$12$ ft і радіусом основи$4$ ft. Бак заповнений для початку, і вода перекачується через верхній край бака до тих пір, поки висота води, що залишилася в резервуарі, не складе$4$ футів. Скільки потрібно роботи, щоб відкачати цю кількість води?

Рішення

Танк зображений на малюнку$\PageIndex{7}$. Як ми робили в прикладі з циліндричним резервуаром, ми орієнтуємо$x$ вісь -вертикально, причому походження у верхній частині резервуара, а напрямок вниз - позитивним (крок 1).

Малюнок$\PageIndex{7}$: Бак для води у формі перевернутого конуса.

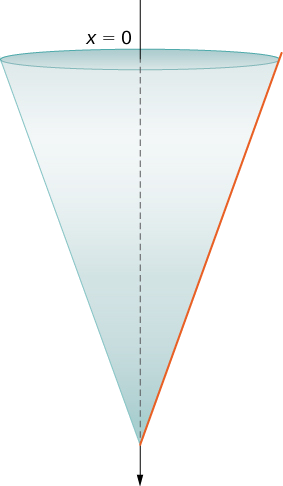
Бак починається повністю і закінчується$4$ футом води, що залишився, тому, виходячи з обраної нами системи відліку, нам потрібно розділити інтервал$[0,8]$. Потім, для$i=0,1,2,…,n$, нехай$P={x_i}$ буде регулярний поділ інтервалу$[0,8]$, а для$i=1,2,…,n$, вибираємо довільну точку$x^∗_i∈[x_{i−1},x_i]$. Ми можемо наблизити обсяг шару за допомогою диска, потім за допомогою аналогічних трикутників знайти радіус диска (рис.$\PageIndex{8}$).

Малюнок$\PageIndex{8}$: За допомогою аналогічних трикутників виражаємо радіус диска з водою.

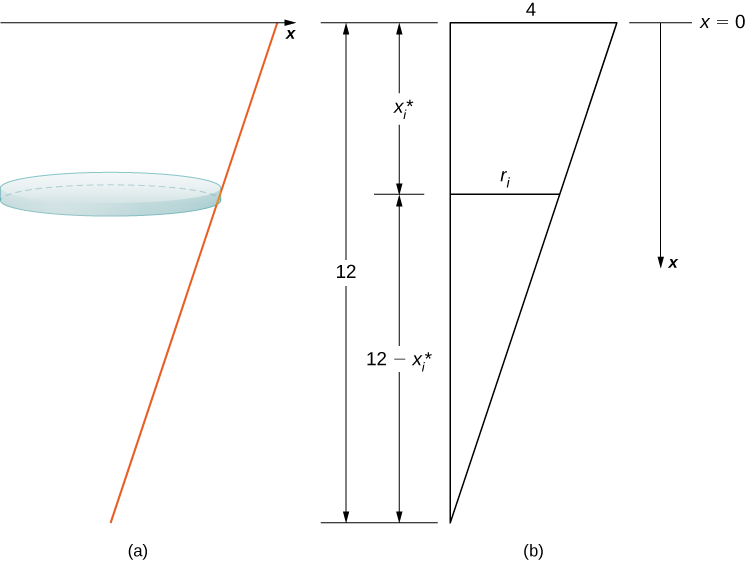
З властивостей подібних трикутників ми маємо

$$\begin{align*} \dfrac{r_i}{12−x^∗_i} =\dfrac{4}{12} \tag{step 1} =\dfrac{1}{3} \\[4pt] 3r_i =12−x^∗_i \\[4pt] r_i =\dfrac{12−x^∗_i}{3} \\[4pt] =4−\dfrac{x^∗_i}{3}. \end{align*}$$

Тоді обсяг диска дорівнює

$$V_i=π \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 2}$$

Вага-щільність води становить$62.4$ фунт/фут ³, тому сила, необхідна для підйому кожного шару, приблизно

$$F_i≈62.4π\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx \tag{step 3}$$

Виходячи зі схеми, відстань, на яку повинна бути піднята вода, становить приблизно$x^∗_i$ фути (крок 4), тому приблизна робота, необхідна для підняття шару, є

$$W_i≈62.4πx^∗_i\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 5}$$

Підсумовуючи роботи, необхідні для підняття всіх верств, отримуємо приблизну величину загальної роботи:

$$W=\sum_{i=1}^nW_i≈\sum_{i=1}^n62.4πx^∗_i \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 6}$$

Приймаючи ліміт, як$n→∞,$ ми отримуємо

$$\begin{align*} W =\lim_{n→∞}\sum^n_{i=1}62.4πx^∗_i(4−\dfrac{x^∗_i}{3})^2Δx \\[4pt] = \int ^8_062.4πx \left(4−\dfrac{x}{3}\right)^2dx \\[4pt] = 62.4π\int ^8_0x \left(16−\dfrac{8x}{3}+\dfrac{x^2}{9}\right)\,dx=62.4π\int ^8_0 \left(16x−\dfrac{8x^2}{3}+\dfrac{x^3}{9}\right)\,dx \\[4pt] =62.4π\left[8x^2−\dfrac{8x^3}{9}+\dfrac{x^4}{36}\right]\bigg|^8_0=10,649.6π≈33,456.7. \end{align*}$$

Потрібно приблизно$33,450$ фут-фунт роботи, щоб спорожнити бак до потрібного рівня.

Вправа$\PageIndex{4}$

Танк має форму перевернутого конуса, з висотою$10$ футів і радіусом основи 6 футів. Резервуар заповнюється на глибину 8 футів для початку, і вода перекачується через верхній край резервуара, поки 3 фути води не залишаться в резервуарі. Скільки потрібно роботи, щоб відкачати цю кількість води?

Підказка

Скористайтеся процесом з попереднього прикладу.

Рішення

Приблизно$43,255.2$ фут-фунт

Гідростатична сила і тиск

У цьому останньому розділі ми дивимося на силу і тиск, що чиниться на предмет, занурений у рідину. В англійській системі сила вимірюється в фунтах. У метричній системі він вимірюється в ньютонах. Тиск - це сила на одиницю площі, тому в англійській системі ми маємо фунти на квадратний фут (або, можливо, частіше, фунти на квадратний дюйм, позначається psi). У метричній системі у нас є ньютони на квадратний метр, які також називають паскалями.

Почнемо з простого випадку плити площі,$A$ зануреної горизонтально у воду на глибині s (рис.$\PageIndex{9}$). Тоді сила, що чиниться на плиту, - це просто вага води над нею, який задається$F=ρAs$, де$ρ$ - щільність ваги води (вага на одиницю об'єму). Щоб знайти гідростатичний тиск - тобто тиск, який чинить вода на занурений об'єкт, ми ділимо силу на площу. Так що тиск є$p=F/A=ρs$.

Малюнок$\PageIndex{9}$: Плита, занурена горизонтально у воду.

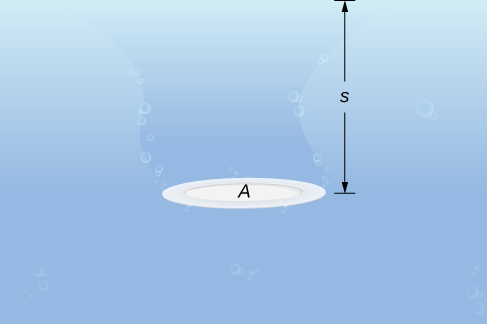
За принципом Паскаля тиск на заданій глибині однаково на всі боки, тому не має значення, занурена плита горизонтально або вертикально. Отже, поки ми знаємо глибину, ми знаємо тиск. Ми можемо застосувати принцип Паскаля, щоб знайти силу, що діє на поверхні, такі як греблі, орієнтовані вертикально. Ми не можемо застосувати формулу$F=ρAs$ безпосередньо, оскільки глибина змінюється від точки до точки на вертикально орієнтованій поверхні. Отже, як ми робили багато разів раніше, ми формуємо розділ, суму Рімана, і, врешті-решт, певний інтеграл для обчислення сили.

Припустимо, тонка пластинка занурена в воду. Ми вибираємо нашу систему відліку таким чином, що$x$ -вісь орієнтована вертикально, причому напрямок вниз є позитивним, а точка$x=0$ відповідає логічній точці відліку. Нехай$s(x)$ позначають глибину в точці х. примітка ми часто дозволяємо$x=0$ відповідати поверхні води. При цьому глибина в будь-якій точці просто задається$s(x)=x$. Однак у деяких випадках ми можемо захотіти вибрати іншу точку відліку для$x=0$, тому ми приступаємо до розробки в більш загальному випадку. Останнім, нехай$w(x)$ позначимо ширину пластини в точці$x$.

Припустимо, що верхній край пластини знаходиться в точці,$x=a$ а нижній край пластини знаходиться в точці$x=b$. Потім, для$i=0,1,2,…,n$, нехай$P={x_i}$ буде регулярний поділ інтервалу$[a,b]$, а для$i=1,2,…,n$, вибираємо довільну точку$x^∗_i∈[x_{i−1},x_i]$. Перегородка ділить пластину на кілька тонких прямокутних смуг (рис.$\PageIndex{10}$).

Малюнок$\PageIndex{10}$: Тонка пластина, занурена вертикально у воду.

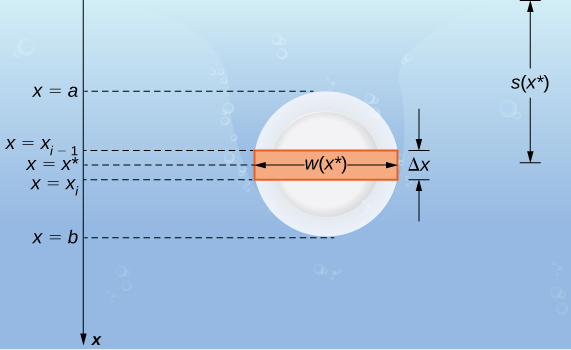
Давайте тепер оцінимо силу на представницькій смузі. Якщо смужка досить тонка, ми можемо ставитися до неї так, ніби вона знаходиться на постійній глибині,$s(x^∗_i)$. У нас тоді є

$$F_i=ρAs=ρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber$$

Склавши зусилля, отримуємо оцінку сили на тарілку:

$$F≈\sum_{i=1}^nF_i=\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber$$

Це сума Рімана, тому взяття межі дає нам точну силу. Отримуємо

$$F=\lim_{n→∞}\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i)=\int ^b_aρw(x)s(x)dx. \label{eqHydrostatic}$$

Оцінка цього інтеграла дає нам силу на тарілці. Ми підсумовуємо це в наступній стратегії вирішення проблем.

Стратегія вирішення проблем: пошук гідростатичної сили

1. Намалюйте малюнок і виберіть відповідну рамку відліку. (Зауважте, що якщо ми виберемо кадр відліку, відмінний від використовуваного раніше, нам, можливо, доведеться відповідно налаштувати Equation\ ref {eqHydrostatic}.)
2. Визначте функції глибини і ширини,$s(x)$ і$w(x).$
3. Визначте вагу-щільність будь-якої рідини, з якою ви працюєте. Вага-щільність води дорівнює$62.4 \,\text{lb/ft}^3$, або$9800 \,\text{N/m}^3$.
4. Використовуйте рівняння для обчислення загальної сили.

Приклад$\PageIndex{5}$: Finding Hydrostatic Force

Жолоб для води довжиною 15 футів має кінці у формі перевернутих рівнобедрених трикутників, з основою 8 футів і висотою 3 фути. Знайдіть силу на одному кінці корита, якщо корито наповнене водою.

Рішення

$\PageIndex{11}$На малюнку зображено жолоб і більш детальний вигляд одного кінця.

Малюнок$\PageIndex{11}$: (а) Жолоб для води з трикутним перетином. (b) Розміри одного кінця жолоба для води.

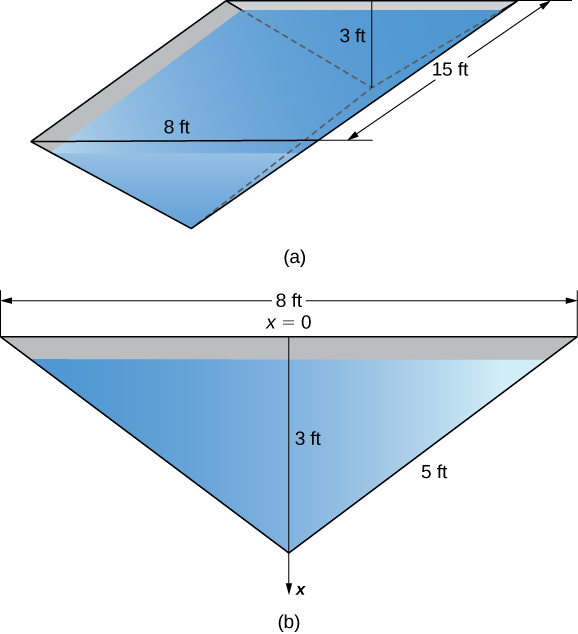
Виберіть кадр відліку з$x$ віссю -орієнтованою вертикально, а напрямок вниз - позитивним. Виберіть верхню частину корита як точку, відповідну$x=0$ (крок 1). Отже, функція глибини є$s(x)=x$. Використовуючи подібні трикутники, ми бачимо, що$w(x)=8−(8/3)x$ (крок 2). Тепер вагова щільність води дорівнює$62.4 \,\text{lb/ft}^3$ (крок 3), тому застосовуючи Equation\ ref {eqHydrostatic}, отримаємо

$$\begin{align*} F =\int ^b_aρw(x)s(x)dx \\[4pt] = \int ^3_062.4 \left(8−\dfrac{8}{3}x\right) x \,dx=62.4\int ^3_0 \left(8x−\dfrac{8}{3}x^2 \right)dx \\[4pt] = \left.62.4 \left[4x^2−\dfrac{8}{9}x^3\right]\right|^3_0=748.8. \end{align*}$$

Вода чинить силу 748,8 фунтів на кінець корита (крок 4).

Вправа$\PageIndex{5}$

Водяний жолоб довжиною 12 м має кінці у формі перевернутих рівнобедрених трикутників, з основою 6 м і висотою 4 м Знайдіть силу на одному кінці корита, якщо жолоб наповнений водою.

Підказка

Дотримуйтесь стратегії вирішення проблем і процесу з попереднього прикладу.

Рішення

$156,800$N

Приклад$\PageIndex{6}$: Finding Hydrostatic Force

Тепер ми повертаємо нашу увагу на греблю Гувера, згадану на початку цієї глави. Фактична гребля арочна, а не рівна, але ми збираємося зробити деякі спрощуючі припущення, щоб допомогти нам з розрахунками. Припустимо, що обличчя греблі Гувера має форму рівнобедреної трапеції з нижньою основою 750 футів, верхньою основою 1250 футів і висотою 750 футів (див. Наступний малюнок).

Коли водосховище заповнене, максимальна глибина озера Мід становить близько 530 футів, а поверхня озера приблизно на 10 футів нижче вершини греблі (див. Наступний малюнок).

Малюнок$\PageIndex{12}$: Спрощена модель греблі Гувера з передбачуваними розмірами.

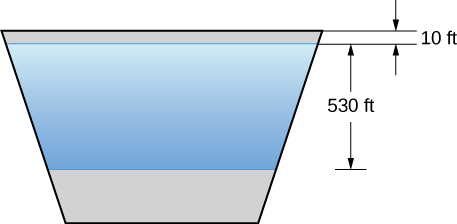
1. Знайдіть силу на обличчі греблі, коли водосховище заповнене.
2. Південний захід Сполучених Штатів переживає посуху, а поверхня озера Мід знаходиться приблизно на 125 футів нижче, де було б, якби водосховище було заповнено. Яка сила на обличчі греблі за цих обставин?

Рішення:

а.

Починаємо з встановлення системи відліку. Як завжди, ми вибираємо орієнтувати$x$ -вісь вертикально, причому напрямок вниз є позитивним. Цього разу, однак, ми збираємося дозволити$x=0$ представляти верхню частину греблі, а не поверхню води. Коли водосховище заповнене, поверхня води знаходиться на$10$ футах нижче вершини греблі, так$s(x)=x−10$ (див. Наступний малюнок).

Малюнок$\PageIndex{13}$: Спочатку вибираємо систему відліку.

Щоб знайти функцію width, знову переходимо до аналогічних трикутників, як показано на малюнку нижче.

Малюнок$\PageIndex{14}$: Використовуємо аналогічні трикутники для визначення функції ширини греблі. (а) передбачувані розміри греблі; (б) виділення подібних трикутників.

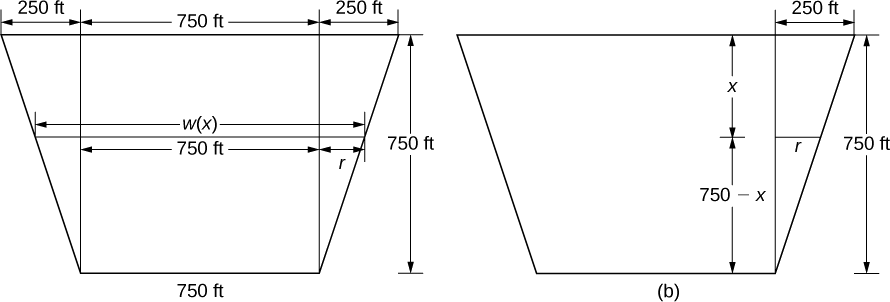
З малюнка ми бачимо, що$w(x)=750+2r$. Використовуючи властивості подібних трикутників, отримаємо$r=250−(1/3)x$. Таким чином,

$$w(x)=1250−\dfrac{2}{3}x \tag{step 2}$$

Використовуючи вагову щільність$62.4$ фунт/фут ^{3 (крок 3}) і застосовуючи Equation\ ref {eqHydrostatic}, отримаємо

\ [\ почати {вирівнювати*} F =\ int^b_a ρw (x) s (x)\, dx\\ [4pt]
=\ int ^ {540} _ {10} 62.4\ ліворуч (1250−\ dfrac {2} {3} х\ праворуч) (x−10)\, dx\\ [4pt]
=62.4\ int ^ {540} _ {10} −\ dfrac {2} {3} [x^2−1885x+18750]\, dx\\ [4pt]
=−62,4\ ліворуч (\ dfrac {2} {3}\ праворуч)\ ліворуч [\ dfrac {x^3} {3} −\ dfrac {1885x^2} {2} +18750x\ праворуч]\ big|^ {540} _ {10} ≈8,832 245,000\,\ текст {lb} =4,416,122,5\,\ текст {t}. \ end {вирівнювати*}\]

Зверніть увагу на зміну від фунтів до тонн ($2000$фунт =$1$ тонна) (крок 4). Це змінює нашу функцію$s(x)$ глибини та наші межі інтеграції. У нас є$s(x)=x−135$. Нижня межа інтеграції - 135. Залишається верхня межа$540$. Оцінюючи інтеграл, отримуємо

\ [\ почати {вирівнювати*} F =\ int^b_aρ w (x) s (x)\, dx\\ [4pt]
=\ int ^ {540} _ {135} 62.4\ ліворуч (1250−\ dfrac {2} {3} х\ праворуч) (x−135)\, dx\\ [4pt]
=−62.4 (\ dfrac {2} 3})\ int ^ {540} _ {135} (x−1875) (x−135)\, dx=−62.4\ ліворуч (\ dfrac {2} {3}\ праворуч)\ int ^ {540} _ {135} (x^2−2010x+253125)\, dx\\ [4pt]
=−62.4\ ліворуч (\ dfrac {2} {3}\ праворуч)\ лівий [\ dfrac {x^3} {3} −1005x^2+253125x\ праворуч]\ великий | ^ {540} _ {135} ≈5 015 230 000\,\ текст {lb} =2,507 615\,\ текст {t}. \ end {вирівнювати*}\]

Вправа$\PageIndex{6}$

Коли водойма знаходиться на середньому рівні, поверхня води приблизно на 50 футів нижче, де вона була б, якби водойма була заповнена. Яка сила на обличчі греблі за цих обставин?

Підказка

Змініть функцію глибини$s(x),$ та межі інтеграції.

Рішення

Приблизно 7 164 520 000 фунтів або 3 582 260 т

Ключові поняття

• Кілька фізичних застосувань певного інтеграла поширені в техніці та фізиці.
• Певні інтеграли можуть бути використані для визначення маси об'єкта, якщо відома його функція щільності.
• Робота також може бути розрахована з інтеграції силової функції, або при протидії силі тяжіння, як в задачі накачування.
• Певні інтеграли також можуть бути використані для обчислення сили, що чиниться на об'єкт, занурений в рідину.

Ключові рівняння

• Маса одновимірного об'єкта

$\displaystyle m=\int ^b_aρ(x)dx$

• Маса кругового об'єкта

$\displaystyle m=\int ^r_02πxρ(x)dx$

• Робота, виконана над об'єктом

$\displaystyle W=\int ^b_aF(x)dx$

• Гідростатична сила на плиті

$\displaystyle F=\int ^b_aρw(x)s(x)dx$

Глосарій

функція щільності

функція щільності описує, як маса розподіляється по об'єкту; це може бути лінійна щільність, виражена через масу на одиницю довжини; щільність площі, виражена через масу на одиницю площі; або об'ємна щільність, виражена через масу на одиницю об'єму; ваго-щільність також використовується для опису вага (а не маса) на одиницю об'єму

Закон Гука

цей закон стверджує, що сила, необхідна для стиснення (або подовження) пружини, пропорційна відстані, яку пружина була стиснута (або розтягнута) від рівноваги; іншими словами$F=kx$, де$k$ постійна

гідростатичний тиск

тиск, що чиниться водою на занурений об'єкт

робота

кількість енергії, необхідної для переміщення об'єкта; у фізиці, коли сила постійна, робота виражається як добуток сили і відстані