3.8: Неявна диференціація
- Page ID
- 62261
- Знайти похідну складної функції за допомогою неявної диференціації.
- Використовуйте неявне диференціювання для визначення рівняння дотичної прямої.
Ми вже вивчали, як знайти рівняння дотичних ліній до функцій і швидкість зміни функції в певній точці. У всіх цих випадках ми мали явне рівняння для функції та чітко диференціювали ці функції. Припустимо замість цього, що ми хочемо визначити рівняння дотичної лінії до довільної кривої або швидкість зміни довільної кривої в точці. У цьому розділі ми вирішуємо ці завдання шляхом знаходження похідних функцій, які визначають\(y\) неявно в терміні\(x\).
неявна диференціація
У більшості обговорень математики, якщо залежна змінна\(y\) є функцією незалежної змінної\(x\), ми виражаємо y термінами\(x\). Якщо це так, ми говоримо, що\(y\) це явна функція\(x\). Наприклад, коли ми пишемо рівняння\(y=x^2+1\), ми визначаємо y явно з точки зору\(x\). З іншого боку, якщо зв'язок між функцією\(y\) та змінною\(x\) виражається рівнянням, де не\(y\) виражається повністю через терміни\(x\), ми говоримо, що рівняння визначається\(y\) неявно з точки зору\(x\). Наприклад, рівняння\(y−x^2=1\) визначає функцію\(y=x^2+1\) неявно.
Неявна диференціація дозволяє знайти нахили дотичних до кривих, які явно не є функціями (вони провалюють тест вертикальної лінії). Ми використовуємо ідею, що частини\(y\) є функціями, які задовольняють заданому рівнянню, але що y насправді не є функцією\(x\).
Загалом, рівняння визначає функцію неявно, якщо функція задовольняє цьому рівнянню. Рівняння може визначати безліч різних функцій неявно. Наприклад, функції
\[y=\sqrt{25−x^2}\nonumber \]
і
\[y=\begin{cases}\sqrt{25−x^2}, & \text{if }−5≤x<0\\ −\sqrt{25−x^2}, & \text{if }0≤x≤5\end{cases}\nonumber \]
які проілюстровані на малюнку\(\PageIndex{1}\), є лише двома з багатьох функцій, визначених неявно рівнянням\(x^2+y^2=25\).
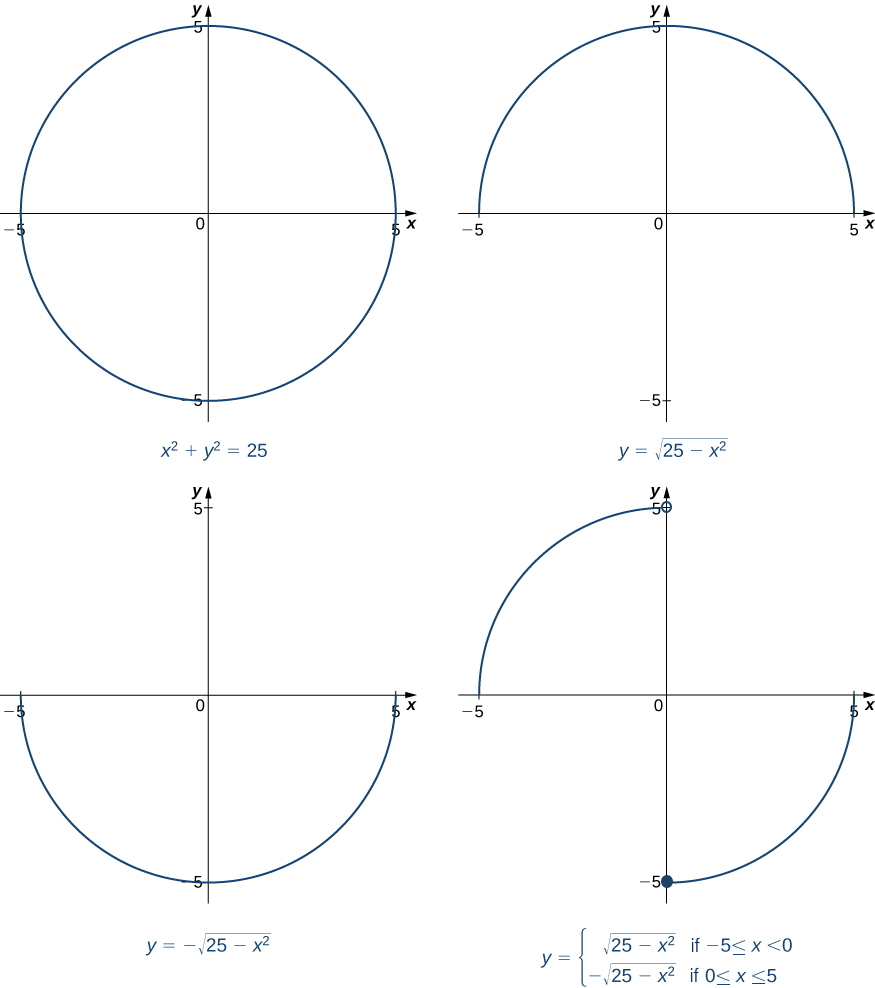
Якщо ми хочемо знайти нахил прямої дотичної до графіка\(x^2+y^2=25\) в точці\((3,4)\), ми могли б оцінити похідну функції\(y=\sqrt{25−x^2}\) в\(x=3\). З іншого боку, якщо ми хочемо нахил дотичної лінії в точці\((3,−4)\), ми могли б використовувати похідну від\(y=−\sqrt{25−x^2}\). Однак не завжди легко вирішити функцію, визначену неявно рівнянням. На щастя, техніка неявної диференціації дозволяє знайти похідну від неявно визначеної функції, ніколи не вирішуючи для функції явно. Процес знаходження з\(\dfrac{dy}{dx}\) використанням неявної диференціації описано в наступній стратегії розв'язання задач.
Щоб виконати неявну диференціацію на рівнянні, що визначає функцію\(y\) неявно через змінну\(x\), скористайтеся наступними кроками:
- Візьміть похідну обох сторін рівняння. Майте на увазі, що\(y\) це функція\(x\). Отже, тоді як\[\dfrac{d}{dx}(\sin x)=\cos x\nonumber \] і\[\dfrac{d}{dx}(\sin y)=\cos y\cdot\dfrac{dy}{dx}\nonumber \] тому, що ми повинні використовувати правило ланцюга для диференціації\(\sin y\) щодо\(x\).
- Перепишіть рівняння так, щоб всі члени\(dy/dx\), що містять, були зліва, а всі члени,\(dy/dx\) які не містять, - праворуч.
- Фактор\(dy/dx\) зліва.
- \(dy/dx\)Розв'яжіть for шляхом ділення обох сторін рівняння відповідним алгебраїчним виразом.
Припускаючи,\(y\) що визначено неявно рівнянням\(x^2+y^2=25\), знайдіть\(\dfrac{dy}{dx}\).
Рішення
Дотримуйтесь кроків стратегії вирішення проблем.
| \(\dfrac{d}{dx}(x^2+y^2)=\dfrac{d}{dx}(25)\) | Крок 1. Диференціювати обидві сторони рівняння. |
| \(\dfrac{d}{dx}(x^2)+\dfrac{d}{dx}(y^2)=0\) | Крок 1.1. Скористайтеся правилом суми зліва. Праворуч\(\dfrac{d}{dx}(25)=0\). |
| \(2x+2y\dfrac{dy}{dx}=0\) | Крок 1.2. Візьміть похідні, так\(\dfrac{d}{dx}(x^2)=2x\) і\(\dfrac{d}{dx}(y^2)=2y\dfrac{dy}{dx}\). |
| \(2y\dfrac{dy}{dx}=−2x\) | Крок 2. Тримайте умови з\(\dfrac{dy}{dx}\) ліворуч. Решта терміни перемістіть вправо. |
| \(\dfrac{dy}{dx}=−\dfrac{x}{y}\) | Крок 4. Розділіть обидві сторони рівняння на\(2y\). (Крок 3 в даному випадку не застосовується.) |
Аналіз
Зверніть увагу, що результуючий вираз for\(\dfrac{dy}{dx}\) є термінами як незалежної змінної, так\(x\) і залежної змінної\(y\). Хоча в деяких випадках це може бути можливо\(\dfrac{dy}{dx}\) висловити\(x\) лише термінами, як правило, це неможливо зробити.
Припускаючи,\(y\) що визначено неявно рівнянням\(x^3\sin y+y=4x+3\), знайдіть\(\dfrac{dy}{dx}\).
Рішення
| \(\dfrac{d}{dx}(x^3\sin y+y)=\dfrac{d}{dx}(4x+3)\) | Крок 1: Диференціюйте обидві сторони рівняння. |
| \(\dfrac{d}{dx}(x^3\sin y)+\dfrac{d}{dx}(y)=4\) | Крок 1.1: Застосуйте правило суми зліва. Праворуч,\(\dfrac{d}{dx}(4x+3)=4\). |
| \(\left(\dfrac{d}{dx}(x^3)⋅\sin y+\dfrac{d}{dx}(\sin y)⋅x^3\right)+\dfrac{dy}{dx}=4\) | Крок 1.2: Використовуйте правило продукту, щоб знайти\(\dfrac{d}{dx}(x^3\sin y)\). Спостерігайте за цим\(\dfrac{d}{dx}(y)=\dfrac{dy}{dx}\). |
| \(3x^2\sin y+(\cos y\dfrac{dy}{dx})⋅x^3+\dfrac{dy}{dx}=4\) | Крок 1.3: Ми знаємо\(\dfrac{d}{dx}(x^3)=3x^2\). Використовуйте правило ланцюга для отримання\(\dfrac{d}{dx}(\sin y)=\cos y\dfrac{dy}{dx}\). |
| \(x^3\cos y\dfrac{dy}{dx}+\dfrac{dy}{dx}=4−3x^2\sin y\) | Крок 2: Зберігайте всі терміни, що\(\dfrac{dy}{dx}\) містяться ліворуч. Перемістіть всі інші терміни вправо. |
| \(\dfrac{dy}{dx}(x^3\cos y+1)=4−3x^2\sin y\) | Крок 3: Фактор\(\dfrac{dy}{dx}\) зліва. |
| \(\dfrac{dy}{dx}=\dfrac{4−3x^2\sin y}{x^3\cos y+1}\) | Крок 4: Вирішіть для\(\dfrac{dy}{dx}\), розділивши обидві сторони рівняння на\(x^3\cos y+1\). |
Знайти,\(\dfrac{d^2y}{dx^2}\) якщо\(x^2+y^2=25\).
Рішення
У\(\PageIndex{1}\) прикладі ми це показали\(\dfrac{dy}{dx}=−\dfrac{x}{y}\). Ми можемо взяти похідну обох сторін цього рівняння, щоб знайти\(\dfrac{d^2y}{dx^2}\).
\ (\ begin {align*}\ dfrac {d^2y} {dx^2} &=\ dfrac {d} {dy}\ ліворуч (−\ dfrac {x} {y}\ праворуч) &\ text {диференціювати обидві сторони}\ dfrac {dx} {y}.\ [4pt]
== −\ dfrac {\ left (1⋅y−x\ dfrac {dy} {dx}\ праворуч)} {y^2} &\ text {Використовуйте правило частки, щоб знайти}\ dfrac {d} {dy}\ left (−\ dfrac {x} {y} \ праворуч).\\ [4pt]
&=\ dfrac {−y+x\ dfrac {dy} {dx}} {y^2} &\ текст {спростити.}\\ [4pt]
&=\ dfrac {−y+x\ ліворуч (−\ dfrac {x} {y}\ праворуч)} {y^2} &\ text {Заміна}\ frac {dy} {dx} =−\ dfrac {x} {y}.\\ [4pt]
&=\ dfrac {−y^2−x^2} {y^3} &\ текст {спростити.} \ end {вирівнювати*}\)
На даний момент ми знайшли вираз для\(\dfrac{d^2y}{dx^2}\). Якщо ми виберемо, ми можемо спростити вираз далі, нагадавши, що\(x^2+y^2=25\) і зробивши цю підстановку в чисельнику для отримання\(\dfrac{d^2y}{dx^2}=−\dfrac{25}{y^3}\).
Знайти\(\dfrac{dy}{dx}\) для\(y\) визначеного неявно рівнянням\(4x^5+\tan y=y^2+5x\).
- Підказка
-
Дотримуйтесь стратегії вирішення проблем, не забуваючи застосовувати правило ланцюга для диференціації\(\tan y\) і\(y^2\).
- Відповідь
-
\[\dfrac{dy}{dx}=\dfrac{5−20x^4}{\sec^2y−2y} \nonumber \]
Пошук дотичних ліній неявно
Тепер, коли ми побачили техніку неявної диференціації, ми можемо застосувати її до задачі знаходження рівнянь дотичних ліній до кривих, описаних рівняннями.
Знайдіть рівняння прямої дотичної до кривої\(x^2+y^2=25\) в точці\((3,−4)\).
Рішення
Хоча ми могли б знайти це рівняння без використання неявної диференціації, використання цього методу значно полегшує його. У\(\PageIndex{1}\) прикладі ми знайшли\(\dfrac{dy}{dx}=−\dfrac{x}{y}\).
Нахил дотичної лінії знаходять шляхом підстановки\((3,−4)\) в цей вираз. Отже, нахил дотичної лінії дорівнює\(\dfrac{dy}{dx}\Big|_{(3,−4)}=−\dfrac{3}{−4}=\dfrac{3}{4}\).
Використовуючи точку\((3,−4)\) і ухил\(\dfrac{3}{4}\) в рівнянні точка-нахил прямої, отримаємо рівняння\(y=\dfrac{3}{4}x−\dfrac{25}{4}\) (рис.\(\PageIndex{2}\)).
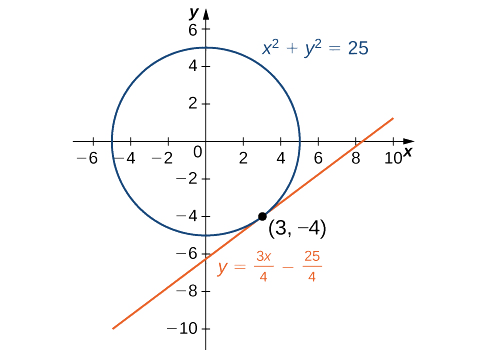
Знайдіть рівняння прямої дотичної до графіка\(y^3+x^3−3xy=0\) в точці\(\left(\frac{3}{2},\frac{3}{2}\right)\) (рис.\(\PageIndex{3}\)). Ця крива відома як листок (або лист) Декарта.
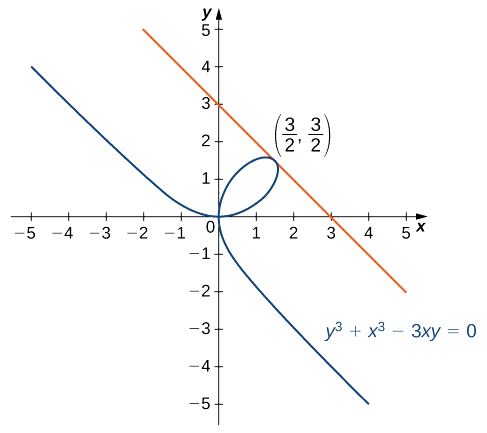
Рішення
Почніть з пошуку\(\dfrac{dy}{dx}\).
\(\dfrac{d}{dx}\big(y^3+x^3−3xy\big)=\dfrac{d}{dx}\big(0\big)\)
\(3y^2\dfrac{dy}{dx}+3x^2−\left(3y+3x\dfrac{dy}{dx}\right)=0\)
\(3y^2\dfrac{dy}{dx}+3x^2−3y-3x\dfrac{dy}{dx}=0\)
\(\left(3y^2-3x\right)\dfrac{dy}{dx}=3y-3x^2\)
\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\).
Далі\(\left(\frac{3}{2},\frac{3}{2}\right)\) підставляємо в,\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\) щоб знайти нахил дотичної лінії:
\(\dfrac{dy}{dx}\Bigg|_{\left(\frac{3}{2},\frac{3}{2}\right)}=−1\).
Нарешті, підставляємо в рівняння точки-нахилу прямої, щоб отримати
\(y=−x+3\).
У простій відеогрі ракета рухається по еліптичній орбіті, шлях якої описується рівнянням\(4x^2+25y^2=100\). Ракета може вести вогонь ракетами по лініях, дотичним до її шляху. Мета гри полягає в тому, щоб знищити вхідний астероїд, що рухається вздовж позитивної\(x\) осі в бік\((0,0)\). Якщо ракета вистрілює ракету, коли вона розташована за адресою\(\left(3,\frac{8}{5}\right)\), де вона буде перетинатися з\(x\) віссю?
Рішення
Щоб вирішити цю задачу, ми повинні визначити, де пряма дотична до графа
\(4x^2+25y^2=100\)at\(\left(3,\frac{8}{5}\right)\) перетинає\(x\) -вісь. Почніть з пошуку\(\dfrac{dy}{dx}\) неявно.
Диференціюючи, ми маємо
\(8x+50y\dfrac{dy}{dx}=0.\)
Рішення для\(\dfrac{dy}{dx}\),
у нас є
\(\dfrac{dy}{dx}=−\dfrac{4x}{25y}\).
Нахил дотичної лінії дорівнює\(\dfrac{dy}{dx}\Bigg|_{\left(3,\frac{8}{5}\right)}=−\dfrac{3}{10}\). Рівняння дотичної прямої є\(y=−\dfrac{3}{10}x+\dfrac{5}{2}\). Щоб визначити, де пряма перетинає\(x\) -вісь, вирішіть\(0=−\dfrac{3}{10}x+\dfrac{5}{2}\). Рішення є\(x=\dfrac{25}{3}\). Ракета перетинає\(x\) -вісь в точці\(\left(\frac{25}{3},0\right)\).
Знайдіть рівняння прямої дотичної до гіперболи\(x^2−y^2=16\) в точці\((5,3)\).
- Підказка
-
\(\dfrac{dy}{dx}=\dfrac{x}{y}\)
- Відповідь
-
\(y=\dfrac{5}{3}x−\dfrac{16}{3}\)
Ключові концепції
- Використовується неявна диференціація для пошуку похідних неявно визначених функцій (функцій, визначених рівняннями).
- Використовуючи неявне диференціювання, ми можемо знайти рівняння дотичної лінії до графіка кривої.
Глосарій
- неявна диференціація
- це техніка обчислення\(\dfrac{dy}{dx}\) для функції, визначеної рівнянням, що здійснюється шляхом диференціації обох сторін рівняння (пам'ятаючи розглядати змінну\(y\) як функцію) та розв'язування для\(\dfrac{dy}{dx}\)
