2.5: Точне визначення межі
- Page ID
- 62365
- Опишіть епсилон-дельта визначення межі.
- Застосуйте визначення epsilon-delta, щоб знайти межу функції.
- Охарактеризуйте визначення епсилон-дельта односторонніх меж та нескінченних меж.
- Використовуйте визначення epsilon-delta, щоб довести граничні закони.
До теперішнього часу ви перейшли від самого неформального визначення межі у введенні цієї глави до інтуїтивного розуміння межі. На цьому етапі ви повинні мати дуже сильне інтуїтивне відчуття того, що означає межа функції і як ви можете її знайти. У цьому розділі ми перетворюємо це інтуїтивне уявлення про обмеження в формальне визначення, використовуючи точну математичну мову. Формальне визначення межі цілком можливо одне з найскладніших визначень, з якими ви зіткнетеся на початку вивчення обчислення; однак, це добре варто будь-яких зусиль, які ви докладаєте, щоб узгодити його з інтуїтивним поняттям межі. Розуміння цього визначення є ключем, який відкриває двері для кращого розуміння обчислення.
Кількісна оцінка близькості
Перш ніж заявити про формальне визначення межі, ми повинні представити кілька попередніх ідей. Нагадаємо, що відстань між двома точками\(a\) і\(b\) на числовій лінії задається |\(a−b\) |.
- Твердження |\(f(x)−L |<ε\) можна інтерпретувати як: Відстань між\(f(x)\) і\(L\) менше\(ε\).
- Твердження\(0<|x−a|<δ\) може трактуватися як:\(x≠a\) і відстань між\(x\) і\(a\) менше\(δ\).
Також важливо подивитися на наступні еквіваленти за абсолютним значенням:
- Заява |\(f(x)−L|<ε\) еквівалентна твердженню\(L−ε<f(x)<L+ε\).
- \(0<|x−a|<δ\)Заява еквівалентна заяві\(a−δ<x<a+δ\) і\(x≠a\).
За допомогою цих роз'яснень ми можемо констатувати формальне визначення межі епсилон-дельта.
\(f(x)\)Дозволяти визначатися для всього\(x≠a\) відкритого інтервалу, що містить\(a\). \(L\)Дозволяти бути дійсним числом. Тоді
\[\lim_{x→a}f(x)=L \nonumber \]
якщо, для кожного\(ε>0\), існує такий\(δ>0\), що якщо\(0<|x−a|<δ\), то\(|f(x)−L|<ε\).
Це визначення може здатися досить складним з математичної точки зору, але його стає легше зрозуміти, якщо розбити його по словосполученню. Саме твердження включає в себе те, що називається універсальним квантором (для кожного\(ε>0\)), екзистенціальним квантором (існує а\(δ>0\)), і, нарешті, умовним твердженням (якщо\(0<|x−a|<δ\), то\(|f(x)−L|<ε)\). Давайте подивимося на таблицю\(\PageIndex{1}\), яка розбиває визначення і перекладає кожну частину.
| Визначення | Переклад |
|---|---|
| 1. Для кожного\(ε>0\), | 1. За кожну позитивну\(ε\) віддаленість від\(L\), |
| 2. існує\(δ>0\), | 2. Є позитивна віддаленість\(δ\) від\(a\), |
| 3. такий, що | 3. такий, що |
| 4. якщо\(0<|x−a|<δ\), то\(|f(x)−L|<ε\). | 4. якщо\(x\) ближче, ніж\(δ\) до\(a\) і\(x≠a\),\(f(x)\) то ближче, ніж\(ε\) до\(L\). |
Ми можемо краще впоратися з цим визначенням, подивившись на визначення геометрично. \(\PageIndex{1}\)На малюнку показані можливі значення\(δ\)\(ε>0\) для різних варіантів для заданої функції\(f(x)\)\(a\), числа та обмеження\(L\) на\(a\). Зверніть увагу, що як ми вибираємо менші значення\(ε\) (відстань між функцією і межа), ми завжди можемо знайти досить\(δ\) маленький, так що якщо ми вибрали\(x\)\(δ\) значення в межах\(a\), то значення\(f(x)\) знаходиться в межах\(ε\) межі \(L\).
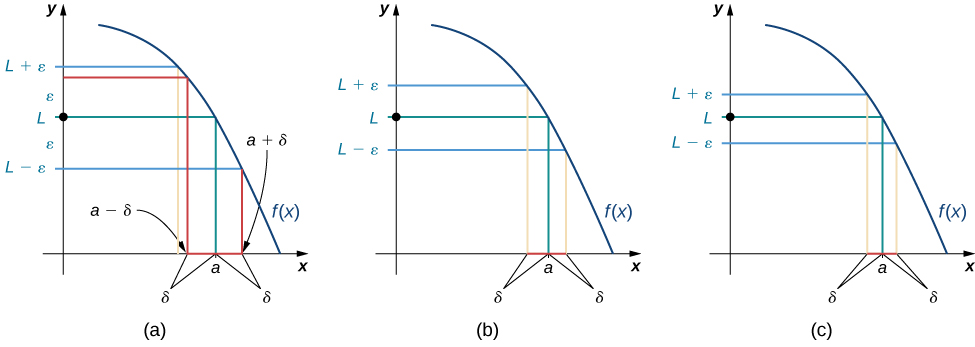
Відвідайте наступний аплет, щоб поекспериментувати з пошуком значень\(δ\) для вибраних значень\(ε\):
Приклад\(\PageIndex{1}\) показує, як можна використовувати це визначення, щоб довести твердження про обмеження певної функції при вказаному значенні.
Доведіть це\(\displaystyle \lim_{x→1} \;(2x+1)=3\).
Рішення
Нехай\(ε>0\).
Перша частина визначення починається «Для кожного\(ε>0\)» Це означає, що ми повинні довести, що все, що слід, вірно незалежно від того, яке позитивне значення\(ε\) вибрано. Зазначаючи «Нехай»\(ε>0\), ми сигналізуємо про наш намір зробити це.
Вибираємо\(δ=\frac{ε}{2}\).
Визначення продовжується з «існує»\(δ>0\). фраза «існує існує» в математичному твердженні завжди є сигналом для полювання на смітника. Іншими словами, ми повинні піти і знайти\(δ\). Отже, звідки саме\(δ=ε/2\) взялися? Існує два основних підходи до відстеження вниз\(δ\). Один метод суто алгебраїчний, а інший - геометричний.
Почнемо з вирішення проблеми з алгебраїчної точки зору. Оскільки в кінцевому підсумку ми хочемо\(|(2x+1)−3|<ε\), ми починаємо з маніпулювання цим виразом:\(|(2x+1)−3|<ε\) еквівалентно\(|2x−2|<ε\), що, в свою чергу, еквівалентно\(|2||x−1|<ε\). Останнє, це еквівалентно\(|x−1|<ε/2\). Таким чином, здавалося б,\(δ=ε/2\) доречно.
Ми також можемо знайти\(δ\) за допомогою геометричних методів. Малюнок\(\PageIndex{2}\) демонструє, як це робиться.
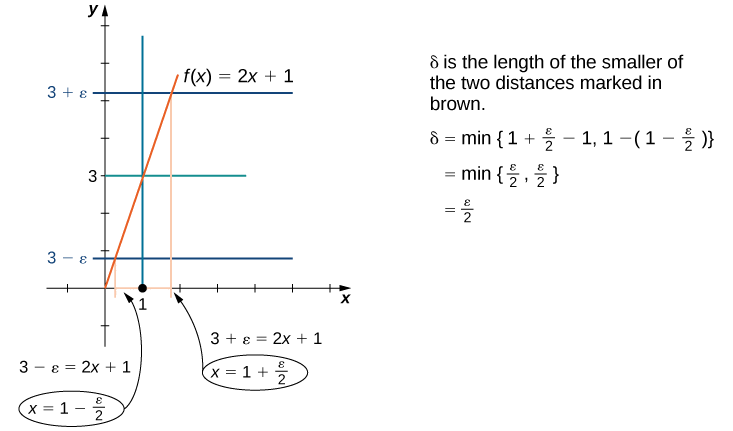
Припустимо\(0<|x−1|<δ\). Коли\(δ\) був обраний, наша мета - показати, що якщо\(0<|x−1|<δ\), то\(|(2x+1)−3|<ε\). Щоб довести будь-яке твердження виду «Якщо це, то що», ми починаємо з припущення «це» і намагаємося отримати «що».
Таким чином,
\(|(2x+1)−3|=|2x−2|\)властивість абсолютного значення
\(=|2(x−1)|\)
\(=|2||x−1|\)\(|2|=2\)
\(=2|x−1|\)
\(<2⋅δ \)ось де ми використовуємо припущення, що\(0<|x−1|<δ\)
\(=2⋅\frac{ε}{2}=ε\)ось де ми використовуємо наш вибір\(δ=ε/2\)
Аналіз
У цій частині доказу ми почали з\(|(2x+1)−3|\) і використовували наше припущення\(0<|x−1|<δ\) в ключовій частині ланцюга нерівностей,\(|(2x+1)−3|\) щоб стати меншим за ε. Ми могли б так само легко маніпулювати передбачуваною нерівністю\(|(2x+1)−3|<ε\),\(0<|x−1|<δ\) щоб досягти наступного:
\(0<|x−1|<δ⇒|x−1|<δ\)
\(⇒−δ<x−1<δ\)
\(⇒−\frac{ε}{2}<x−1<\frac{ε}{2}\)
\(⇒−ε<2x−2<ε\)
\(⇒|2x−2|<ε\)
\(⇒|(2x+1)−3|<ε.\)
Тому\(\displaystyle \lim_{x→1} \;(2x+1)=3.\) (Завершивши доказ, ми констатуємо, чого ми досягли.)
Після видалення всіх зауважень ось остаточний варіант доказу:
Нехай\(ε>0\).
Вибираємо\(δ=ε/2\).
Припустимо\(0<|x−1|<δ\).
Таким чином,
\ (\ почати {вирівнювати*} | (2x+1) −3| &= |2x−2|\\ [4pt]
&=|2 (x−1) |\\ [4pt] &=|2||x−1|\\ [4pt]
&=2|x−1|\\ [
4pt]
&<2⋅δ\ [4pt] &= 2⋅\\ [4pt] &<2⋅\ [4пт]
&<2⋅\ [4pt] &=2⋅\\ фрак ε} {2}\\ [4пт]
&=ε. \ end {вирівнювати*}\)
Тому,\(\displaystyle \lim_{x→1} \;(2x+1)=3\).
Наступна стратегія вирішення проблем узагальнює тип доказу, який ми розробили в прикладі\(\PageIndex{1}\).
- Почнемо доказ з наступного твердження: Нехай\(ε>0\).
- Далі нам потрібно отримати значення для\(δ\). Після того, як ми отримали це значення, робимо наступну заяву, заповнюючи бланк з нашим вибором\(δ\): Вибираємо\(δ=\) _______.
- Наступним твердженням у доказі має бути (на цьому етапі ми заповнюємо наше задане значення для\(a\)): Припустимо\(0<|x−a|<δ\).
- Далі, виходячи з цього припущення, нам потрібно показати\(|f(x)−L|<ε\), що, де\(f(x)\) і\(L\) знаходяться наша функція\(f(x)\) і наша межа\(L\). У якийсь момент нам потрібно використовувати\(0<|x−a|<δ\).
- Ми завершуємо наш доказ твердженням: Отже,\(\displaystyle \lim_{x→a}f(x)=L\).
Завершіть доказ того,\(\displaystyle \lim_{x→−1}\;(4x+1)=−3\) заповнивши заготовки.
Нехай _____.
Виберіть\(δ=\) _______.
Припустимо\(0<|x\) −_______|\(<δ\).
Таким чином, |________−________|=_________________________________\(ε\).
Рішення
Починаємо з заповнення прогалин, де вибір задається визначенням. Таким чином, ми маємо
Нехай\(ε>0\).
Виберіть\(δ\) =_______.
Припустимо\(0<|x−(−1)|<δ\). (або еквівалентно,\(0<|x+1|<δ\).)
Таким чином,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ\) _______\(ε\).
Орієнтуючись на фінальну лінію доказу, ми бачимо, що слід вибирати\(δ=\frac{ε}{4}\).
Тепер ми завершуємо остаточне написання доказу:
Нехай\(ε>0\).
Вибираємо\(δ=\frac{ε}{4}\).
Припустимо\(0<|x−(−1)|<δ\) (або еквівалентно,\(0<|x+1|<δ\).)
Таким чином,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ=4(ε/4)=ε\).
Завершіть доказ того,\(\displaystyle \lim_{x→2}\;(3x−2)=4\) заповнивши заготовки.
Нехай _______.
Виберіть\(δ\) =_______.
Припустимо\(0<|x−\) ____\(|<\) ____.
Таким чином,
|_______−____|\(=\) __________________________________\(ε\).
Тому,\(\displaystyle \lim_{x→2}\;(3x−2)=4\).
- Підказка
-
Дотримуйтесь начерків Стратегії вирішення проблем, яку ми повністю розробили на прикладі\(\PageIndex{2}\).
- Відповідь
-
Нехай\(ε>0\); вибрати\(δ=\frac{ε}{3}\); припустити\(0<|x−2|<δ\).
Таким чином,\(|(3x−2)−4|=|3x−6|=|3|⋅|x−2|<3⋅δ=3⋅(ε/3)=ε\).
Тому,\(\displaystyle \lim_{x→2}(3x−2)=4\).
У Прикладах\(\PageIndex{1}\) і\(\PageIndex{2}\) докази були досить простими, оскільки функції, з якими ми працювали, були лінійними. У прикладі ми бачимо\(\PageIndex{3}\), як змінити доказ для розміщення нелінійної функції.
Доведіть це\(\displaystyle \lim_{x→2}x^2=4\).
Рішення
1. Нехай\(ε>0\). Перша частина визначення починається «Для кожного»\(ε>0\), тому ми повинні довести, що все, що слід, вірно незалежно від того, яке позитивне значення\(ε\) вибрано. Зазначаючи «Нехай»\(ε>0\), ми сигналізуємо про наш намір зробити це.
2. Без втрати спільності припустимо\(ε≤4\). Два питання представляють себе: Чому ми хочемо\(ε≤4\) і чому це нормально робити це припущення? У відповідь на перше питання: Пізніше, в процесі вирішення для\(δ\), ми виявимо, що\(δ\) передбачає кількість\(\sqrt{4−ε}\). Отже, нам і потрібно\(ε≤4\). У відповідь на друге питання: Якщо ми зможемо виявити\(δ>0\), що «працює» для\(ε≤4\), то він буде «працювати» і для будь-якого\(ε>4\). Майте на увазі, що, хоча завжди нормально ставити верхню межу на ε, ніколи не можна ставити нижню межу (крім нуля)\(ε\).
3. Вибираємо\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). Малюнок\(\PageIndex{3}\) показує, як ми зробили цей вибір\(δ\).
![Цей графік показує, як знайти дельту геометрично для заданого епсилона для наведеного вище доказу. Спочатку функція f (x) = x^2 витягується з [-1, 3]. На осі у відзначається запропонована межа 4, а лінія y=4 проводиться для перетину з функцією at (2,4). Для даного епсилона на осі y вище і нижче 4 відзначаються точки 4 + епсилон і 4 — епсилон. Сині лінії малюються від цих точок для перетину з функцією, де рожеві лінії малюються від точки перетину до осі х. Ці лінії приземляються по обидві сторони від x = 2. Далі ми вирішуємо для цих значень x, які повинні бути позитивними тут. Перший - x^2 = 4 — епсилон, що спрощує x = sqrt (4-епсилон). Наступним є x^2 = 4 + епсилон, що спрощує x = sqrt (4 + епсилон). Дельта є меншою з двох відстаней, тому вона становить min (2 — sqrt (4 — epsilon) і sqrt (4 + epsilon) — 2).](https://math.libretexts.org/@api/deki/files/12354/2.5.2.png)
4. Ми повинні показати: Якщо\(0<|x−2|<δ\), то\(|x^2−4|<ε\), так ми повинні почати з припущення
\(0<|x−2|<δ.\)
Нам насправді не потрібно\(0<|x−2|\) (іншими словами\(x≠2\)) для цього доказу. Так як\(0<|x−2|<δ⇒|x−2|<δ\), це нормально, щоб кинути\(0<|x−2|\).
\(|x−2|<δ.\)
Отже,
\(−δ<x−2<δ.\)
Нагадаємо, що\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). Таким чином,\(δ≥2−\sqrt{4−ε}\) а отже\(−(2−\sqrt{4−ε})≤−δ\). Ми також використовуємо\(δ≤\sqrt{4+ε}−2\) тут. Ми можемо запитати в цей момент: чому ми замінили\(2−\sqrt{4−ε}\)\(δ\) на лівій стороні нерівності і\(\sqrt{4+ε}−2\) на правій стороні нерівності? Якщо ми подивимося на Малюнок\(\PageIndex{3}\), то побачимо, що\(2−\sqrt{4−ε}\) відповідає відстані\(2\) зліва від\(x\) -осі і\(\sqrt{4+ε}−2\) відповідає відстані праворуч. Таким чином,
\(−(2−\sqrt{4−ε})≤−δ<x−2<δ≤\sqrt{4+ε}−2.\)
Спрощуємо вираз зліва:
\(−2+\sqrt{4−ε}<x−2<\sqrt{4+ε}−2\).
Потім до всіх частин нерівності додаємо 2:
\(\sqrt{4−ε}<x<\sqrt{4+ε}.\)
Квадратуємо всі частини нерівності. Це нормально, оскільки всі частини нерівності позитивні:
\(4−ε<x^2<4+ε.\)
Віднімаємо\(4\) з усіх частин нерівності:
\(−ε<x^2−4<ε.\)
Останній,
\(|x^2−4|<ε.\)
5. Тому
\(\displaystyle \lim_{x→2}x^2=4.\)
Знайти δ відповідне\(ε>0\) для доказу того, що\(\displaystyle \lim_{x→9}\sqrt{x}=3\).
- Підказка
-
Намалюйте графік, подібний до графіка в прикладі\(\PageIndex{3}\).
- Відповідь
-
Вибираємо\(δ=\text{min}\{9−(3−ε)^2,\;(3+ε)^2−9\}\).
Геометричний підхід до доведення того, що межа функції приймає певне значення, працює досить добре для деяких функцій. Також неоціненним є розуміння формального визначення межі, яку надає цей метод. Однак ми також можемо підійти до граничних доказів з чисто алгебраїчної точки зору. У багатьох випадках алгебраїчний підхід може не тільки надати нам додаткове розуміння визначення, але й може виявитися простішим. Крім того, алгебраїчний підхід є основним інструментом, який використовується для доказів тверджень про межі. Для прикладу\(\PageIndex{4}\), візьмемо чисто алгебраїчний підхід.
Доведіть, що\(\displaystyle \lim_{x→−1}\;(x^2−2x+3)=6.\)
Рішення
Давайте використаємо наш контур із Стратегії вирішення проблем:
1. Нехай\(ε>0\).
2. Виберіть\(δ=\text{min}\{1,ε/5\}\). Цей вибір\(δ\) може здатися дивним на перший погляд, але він був отриманий, подивившись на нашу кінцеву бажану нерівність:\(∣(x^2−2x+3)−6∣<ε\). Ця нерівність еквівалентна\(|x+1|⋅|x−3|<ε\). У цей момент спокуса просто вибрати\(δ=\frac{ε}{x−3}\) дуже сильна. На жаль, наш вибір\(δ\) повинен залежати тільки від ε і жодної іншої змінної. Якщо ми можемо замінити\(|x−3|\) числовим значенням, наша проблема може бути вирішена. Це місце, де припущення\(δ≤1\) вступає в гру. Вибір\(δ≤1\) тут довільний. Ми могли б так само легко використовувати будь-яке інше позитивне число. У деяких доказах може знадобитися більша уважність у цьому виборі. Тепер, оскільки\(δ≤1\) і\(|x+1|<δ≤1\), ми можемо це показати\(|x−3|<5\). Отже,\(|x+1|⋅|x−3|<|x+1|⋅5\). У цей момент ми розуміємо, що нам теж потрібно\(δ≤ε/5\). Таким чином, вибираємо\(δ=\text{min}\{1,ε/5\}\).
3. Припустимо\(0<|x+1|<δ\). Таким чином,
\[|x+1|<1\text{ and }|x+1|<\frac{ε}{5}. \nonumber \]
Оскільки\(|x+1|<1\), можна зробити висновок, що\(−1<x+1<1\). Таким чином, віднімаючи\(4\) з усіх частин нерівності, отримаємо\(−5<x−3<−1\). Отже,\(|x−3|<5\). Це дає нам
\[\left|(x^2−2x+3)−6\right|=|x+1|⋅|x−3|<\frac{ε}{5}⋅5=ε.\nonumber \]
Тому
\[\lim_{x→−1}\;(x^2−2x+3)=6.\nonumber \]
Завершіть доказ цього\(\displaystyle \lim_{x→1}x^2=1\).
Нехай\(ε>0\); вибрати\(δ=\text{min}\{1,ε/3\}\); припустити\(0<|x−1|<δ\).
Оскільки\(|x−1|<1\), можна зробити висновок, що\(−1<x−1<1\). Таким чином,\(1<x+1<3\). Отже,\(|x+1|<3\).
- Підказка
-
Використовуйте\(\PageIndex{4}\) Example як орієнтир.
- Відповідь
-
\(∣x^2−1∣=|x−1|⋅|x+1|<ε/3⋅3=ε\)
Ви виявите, що, загалом, чим складніша функція, тим більша ймовірність того, що алгебраїчний підхід найлегший у застосуванні. Алгебраїчний підхід також більш корисний для доведення тверджень про межі.
Доведення граничних законів
Зараз ми продемонструємо, як використовувати визначення межі епсилон-дельта для побудови суворого доказу одного з граничних законів. Нерівність трикутника використовується в ключовій точці доказу, тому ми спочатку розглянемо це ключове властивість абсолютного значення.
Нерівність трикутника стверджує, що якщо\(a\) і\(b\) є будь-якими дійсними числами, то\(|a+b|≤|a|+|b|\).
Доведемо наступний граничний закон: Якщо\(\displaystyle \lim_{x→a}f(x)=L\) і\(\displaystyle \lim_{x→a}g(x)=M\), то\(\displaystyle \lim_{x→a}\;(f(x)+g(x))=L+M\).
Нехай\(ε>0\).
Вибирайте\(δ_1>0\) так, щоб якщо\(0<|x−a|<δ_1\), то\(|f(x)−L|<ε/2\).
Вибирайте\(δ_2>0\) так, щоб якщо\(0<|x−a|<δ_2\), то\(|g(x)−M|<ε/2\).
Виберіть\(δ=\text{min}\{δ_1,δ_2\}\).
Припустимо\(0<|x−a|<δ\).
Таким чином,
\(0<|x−a|<δ_1\)і\(0<|x−a|<δ_2\).
Отже,
\ [\ почати {вирівнювати*} | (f (x) +г (х)) − (L+М) |&=| (ф (х) −Л) + (г (х) −М) |\\ [4pt]
&≤|f (x) −L|+|г (х) −М |\\ [4pt]
&<\ frac {ε} {2} +\ frac {2} +\ frac {ε} {2} =ε\ кінець {align*}. \ номер\]
□
Зараз ми досліджуємо, що означає, щоб межа не існувала. Обмеження\(\displaystyle \lim_{x→a}f(x)\) не існує, якщо немає дійсного числа,\(L\) для якого\(\displaystyle \lim_{x→a}f(x)=L\). Таким чином, для всіх дійсних чисел\(L\),\(\displaystyle \lim_{x→a}f(x)≠L\). Щоб зрозуміти, що це означає, розглянемо кожну частину визначення\(\displaystyle \lim_{x→a}f(x)=L\) разом зі своїм протилежним. Переклад визначення наведено в табл\(\PageIndex{2}\).
| Визначення | Навпаки |
|---|---|
| 1. Для кожного\(ε>0\), | 1. Існує\(ε>0\) так, що |
| 2. існує такий\(δ>0\), щоб | 2. для кожного\(δ>0\), |
| 3. якщо\(0<|x−a|<δ\), то\(|f(x)−L|<ε\). | 3. Є\(x\) ситне\(0<|x−a|<δ\) так, що\(|f(x)−L|≥ε\). |
Нарешті, ми можемо констатувати, що це означає, щоб межа не існувала. Межі\(\displaystyle \lim_{x→a}f(x)\) не існує\(L\), якщо для кожного дійсного числа існує дійсне число\(ε>0\) так, що для всіх\(δ>0\), є\(x\) задовольняє\(0<|x−a|<δ\), так що\(|f(x)−L|≥ε\). Давайте застосуємо це в прикладі,\(\PageIndex{5}\) щоб показати, що обмеження не існує.
Показати, що\(\displaystyle \lim_{x→0}\frac{|x|}{x}\) не існує. Графік\(f(x)=|x|/x\) показаний тут:
0, і це лінія без нахилу, яка починається з осі y у відкритому колі (1,0)." src="https://math.libretexts.org/@api/dek...2355/2.5.3.png">
Рішення
Припустимо, що\(L\) це кандидат на ліміт. Виберіть\(ε=1/2\).
Нехай\(δ>0\). Або\(L≥0\) або\(L<0\). Якщо\(L≥0\), то нехай\(x=−δ/2\).
Таким чином,
\(|x−0|=∣−\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
і
\(\left|\frac{∣−\frac{δ}{2}∣}{−\frac{δ}{2}}−L\right|=|−1−L|=L+1≥1>\frac{1}{2}=ε\).
З іншого боку, якщо\(L<0\), то нехай\(x=δ/2\). Таким чином,
\(|x−0|=∣\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
і
\(\left|\frac{∣\frac{δ}{2}∣}{\frac{δ}{2}}−L\right|=|1−L|=|L|+1≥1>\frac{1}{2}=ε\).
Таким чином, при будь-якому значенні\(L\),\(\displaystyle \lim_{x→0}\frac{|x|}{x}≠L.\)
Односторонні межі
Подібно до того, як ми спочатку отримали інтуїтивне розуміння обмежень, а потім перейшли до більш суворого визначення межі, ми тепер переглядаємо односторонні межі. Для цього ми модифікуємо визначення межі epsilon-delta, щоб дати формальні визначення epsilon-delta для меж праворуч і ліворуч у точці. Ці визначення вимагають лише незначних змін від визначення межі. При визначенні межі праворуч нерівність\(0<x−a<δ\) замінює\(0<|x−a|<δ\), що гарантує, що ми враховуємо лише значення\(x\), які більше (праворуч)\(a\). Аналогічно, при визначенні межі зліва нерівність\(−δ<x−a<0\) замінюється\(0<|x−a|<δ\), що гарантує, що ми враховуємо лише значення\(x\), що менше (зліва від)\(a\).
Обмеження праворуч:\(f(x)\) Дозволяти визначатися на відкритому інтервалі форми\((a,b)\), де\(a<b\). Тоді
\[\lim_{x→a^+}f(x)=L \nonumber \]
якщо для кожного\(ε>0\), існує такий\(δ>0\), що якщо\(0<x−a<δ\), то\(|f(x)−L|<ε\).
Обмеження ліворуч:\(f(x)\) Дозволяти визначатися через відкритий інтервал форми\((b,c)\), де\(b<c\). Потім,
\[\lim_{x→c^−}f(x)=L \nonumber \]
якщо для кожного\(ε>0\), існує\(δ>0\) таке, що якщо\( −δ<x−c<0\), то\(|f(x)−L|<ε\).
Доведіть, що
\[\lim_{x→4^+}\sqrt{x−4}=0.\nonumber \]
Рішення
Нехай\(ε>0\).
Виберіть\(δ=ε^2\). Оскільки ми в кінцевому підсумку хочемо\(∣\sqrt{x−4}−0∣<ε\), ми маніпулюємо цією нерівністю, щоб отримати\(\sqrt{x−4}<ε\) або, що еквівалентно\(0<x−4<ε^2\), зробити\(δ=ε^2\) чіткий вибір. Ми також можемо визначити\(δ\) геометрично, як показано на малюнку\(\PageIndex{4}\).
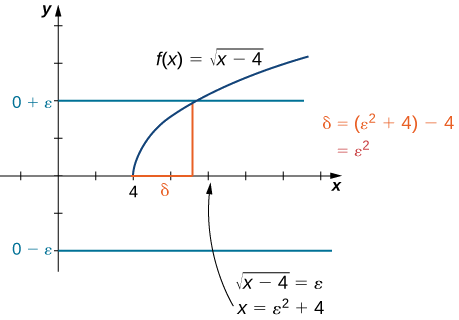
Припустимо\(0<x−4<δ\). Таким чином,\(0<x−4<ε^2\). Отже,\(0<\sqrt{x−4}<ε\). Нарешті,\(\left|\sqrt{x−4}−0\right|<ε\). Тому,\(\displaystyle \lim_{x→4^+}\sqrt{x−4}=0\).
Знайдіть\(δ\) відповідне\(ε\) для доказу цього\(\displaystyle \lim_{x→1^−}\sqrt{1−x}=0\).
- Підказка
-
Намалюйте графік і використовуйте\(\PageIndex{6}\) Example як керівництво для вирішення.
- Відповідь
-
\(δ=ε^2\)
Нескінченні межі
Ми завершуємо процес перетворення наших інтуїтивних ідей різних типів меж у строгі формальні визначення, проводячи формальне визначення нескінченних меж. Щоб мати\(\displaystyle \lim_{x→a}f(x)=+∞\), ми хочемо,\(f(x)\) щоб значення функції стали більшими і більшими, як\(x\) підходи\(a\). Замість вимоги, що\(|f(x)−L|<ε\) для довільно малого,\(ε\) коли\(0<|x−a|<δ\) для малого досить\(δ\), ми хочемо\(f(x)>M\) для довільно великих позитивних,\(M\) коли\(0<|x−a|<δ\) для малих досить\(δ\). Малюнок\(\PageIndex{5}\) ілюструє цю ідею, показуючи значення\(δ\) для послідовно більших значень\(M\).
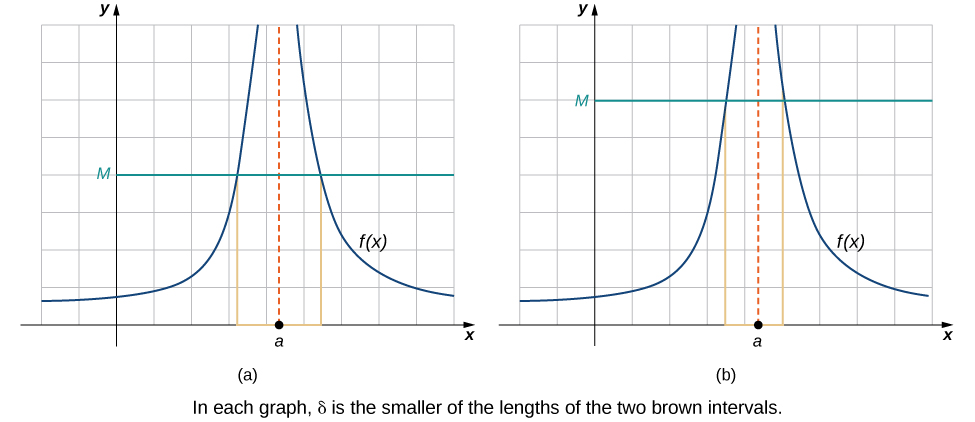
Малюнок\(\PageIndex{5}\): Ці графіки побудови значень\(δ\) for,\(M\) щоб показати це\(\displaystyle \lim_{x→a}f(x)=+∞\).
Нехай\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have an infinite limit
\[\lim_{x→a}f(x)=+∞ \nonumber \]
якщо для кожного\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)>M\).
Нехай\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have a negative infinite limit
\[\lim_{x→a}f(x)=−∞ \nonumber \]
якщо для кожного\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)<−M\).
Доведіть, що\(\displaystyle \lim_{x→3}\frac{1}{(x-3)^2}=\infty.\)
Рішення
Ми використовуємо дуже схожий підхід до нашої попередньої стратегії вирішення проблем. Спочатку знаходимо відповідний\(δ>0\). Потім пишемо наш доказ.
Крок 1: Спочатку знаходимо відповідний\(δ>0\).
1. \(M\)Дозволяти бути будь-яке дійсне число таке, що\(M>0\).
2. Нехай\(f(x) = \dfrac{1}{(x-3)^2} > M\). Потім вирішуємо для виразу\(x - 3\).
Множення обох сторін нерівності на позитивну величину\((x - 3)^2\) і ділення обох сторін на позитивну величину\(M\) дає нам:
\[ \frac{1}{M} > (x-3)^2 \nonumber \]
Взявши квадратний корінь з обох сторін, маємо,
\[ \sqrt{\frac{1}{M}} > |x - 3|. \qquad \quad\left(\text{Remember that }\sqrt{x^2} = |x|.\right)\nonumber \]
Переписування цього твердження дає нам,\(0 < |x-3| < \sqrt{\dfrac{1}{M}}\). З цього вибираємо\(δ = \sqrt{\dfrac{1}{M}}\).
Крок 2: Тепер пишемо доказ.
3. Нехай\(δ = \sqrt{\dfrac{1}{M}}\) і припустимо\(0 < |x-3| < δ = \sqrt{\dfrac{1}{M}}\).
Таким чином,
\[ |x-3| < \sqrt{\frac{1}{M}}. \nonumber \]
Квадрат обидві сторони дає нам,
\[ (x-3)^2 < \frac{1}{M}. \nonumber \]
Беручи взаємні обидві сторони (і пам'ятаючи, що це змінить напрямок нерівності),
\[ \dfrac{1}{(x-3)^2} > M. \nonumber \]
Тому ми довели, що
\[\lim_{x→3}\frac{1}{(x-3)^2}=\infty.\nonumber \]
Дуже схоже доказ знадобиться для ліміту, який дорівнює\(-\infty\).
Зверніть увагу, що односторонній лімітний підхід часто потрібно буде приймати з цим типом ліміту. Наприклад, довести:\(\displaystyle \lim_{x\to 0^+}\frac{1}{x} = \infty\).
Ключові поняття
- Інтуїтивне поняття межі може бути перетворено в суворе математичне визначення, відоме як визначення межі епсилон-дельта.
- Визначення epsilon-delta може бути використано для доведення тверджень про межі.
- Визначення межі епсилон-дельта може бути змінено для визначення односторонніх меж.
- Подібне визначення нескінченної межі може бути використано для доведення тверджень про нескінченні межі.
Глосарій
- epsilon-дельта визначення межі
- \(\displaystyle \lim_{x→a}f(x)=L\)якщо для кожного\(ε>0\), існує\(δ>0\) такий, що якщо\(0<|x−a|<δ\), то\(|f(x)−L|<ε\)
- нерівність трикутника
- Якщо\(a\) і\(b\) є будь-якими дійсними числами, то\(|a+b|≤|a|+|b|\)
- формальне визначення нескінченної межі
- \(\displaystyle \lim_{x→a}f(x)=\infty\)якщо для кожного\(M>0\), існує\(δ>0\) такий, що якщо\(0<|x−a|<δ\), то\(f(x)>M\)
\(\displaystyle \lim_{x→a}f(x)=-\infty\) якщо для кожного\(M>0\), існує\(δ>0\) такий, що якщо\(0<|x−a|<δ\), то\(f(x)<-M\)
Автори та атрибуція
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College), added Example \(\PageIndex{7}\) and entries for infinite limits under Key Concepts and the Glossary.
