7.6: Рідкі сили

У невдалій ситуації, коли автомобіль заїжджає в водойму, загальноприйнята думка полягає в тому, що тиск води на двері швидко буде настільки великим, що вони будуть ефективно невідкритими. (Методи виживання припускають негайно відкрити двері, скотити або розбити вікно, або чекати, поки вода заповнить інтер'єр, в цей момент тиск вирівнюється і двері відкриються. Див. Епізод #72, щоб подивитися, як Адам Севідж перевіряє ці параметри.) Як це може бути правдою? Скільки сил потрібно, щоб відкрити двері зануреного автомобіля? У цьому розділі ми знайдемо відповідь на це питання, вивчивши сили, що чиниться рідинами.

Почнемо з тиску, яке пов'язане з силою наступними рівняннями:

$$\text{Pressure} = \frac{\text{Force}}{\text{Area}}\quad \Leftrightarrow \quad\text{Force} = \text{Pressure}\times\text{Area}.$$

У розрізі рідин ми маємо наступне визначення.

Визначення 26: Тиск рідини

$w$Дозволяти бути вага-щільність рідини. Тиск, що$p$ чиниться на предмет на глибині$d$ в рідині, є$p = w\cdot d$.

Ми використовуємо це визначення, щоб знайти силу, що чиниться на горизонтальному аркуші, враховуючи площу листа.

Приклад$\PageIndex{1}$: Computing fluid force

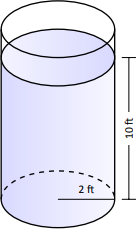
1. Циліндричний резервуар для зберігання має радіус 2 фути і вміщує 10 футів рідини з щільністю ваги 50 фунт/фут$^3$ (рис$\PageIndex{1}$.) Яку силу чинить рідина на підставу циліндра?

Малюнок$\PageIndex{1}$: Циліндричний резервуар на прикладі$\PageIndex{1}$.

1. Прямокутний резервуар, основою якого є квадрат 5 футів, має круглий люк внизу радіусом 2 фути. Резервуар вміщує 10 футів рідини з щільністю ваги 50 фунт/фут$^3$. (Малюнок$\PageIndex{2}$). Яку силу чинить на люк рідиною?

Малюнок$\PageIndex{2}$: Прямокутний резервуар на прикладі$\PageIndex{1}$.

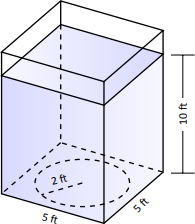
Рішення

1. Використовуючи Definition 26, обчислюємо, що тиск, що чиниться на основу циліндра, становить$w\cdot d = 50 \text{ lb/ft}^3\times 10\text{ ft} = 500$ фунт/фут$^2$. Площа підстави -$\pi\cdot 2^2 = 4\pi$ фути$^2$. Отже, сила, яку надає рідина, $$F = 500\times 4\pi = 6283\text{ lb}. \nonumber$$ Зауважте, що ми ефективно просто обчислили вагу рідини в резервуарі.
2. Розміри бака в цій проблемі не мають значення. Все, що нас турбують, - це розміри люка і глибина залягання рідини. Оскільки розміри люка такі ж, як і підставу бака в попередній частині цього прикладу, як і глибина, ми бачимо, що сила рідини однакова. Тобто,$F = 6283$ lb.

Ключова концепція, яку слід зрозуміти тут, полягає в тому, що ми ефективно вимірюємо вагу 10-футового стовпа води над люком. Розмір бака, що утримує рідину, значення не має.

Попередній приклад демонструє, що обчислення сили, що чиниться на горизонтально орієнтованій пластині, порівняно легко обчислити. А як щодо вертикально орієнтованої пластини? Наприклад, припустимо, у нас є круглий ілюмінатор, розташований збоку від підводного човна. Як ми обчислюємо силу рідини, що чиниться на неї?

Принцип Паскаля стверджує, що тиск, який чинить рідина на глибині, однакове у всіх напрямках. Таким чином, тиск на будь-яку частину пластини, яка знаходиться на 1 фут нижче поверхні води, однаковий незалежно від того, як пластина орієнтована. (Таким чином, занурений на велику глибину порожнистий куб буде не просто «роздавлений» зверху, але і боки будуть м'ятися. Рідина буде чинити силу з усіх боків куба.)

Тому розглянемо вертикально орієнтовану пластину, як показано на малюнку,$\PageIndex{3}$ занурену в рідину з ваговою щільністю$w$. Яка загальна сила рідини, що чиниться на цю пластину? Знаходимо цю силу, спочатку наблизивши силу на малих горизонтальних смугах.

Малюнок$\PageIndex{3}$: Тонка вертикально орієнтована пластина, занурена в рідину з щільністю ваги w.

Нехай верх плити буде на глибині,$b$ а дно нехай знаходиться на глибині$a$. (Зараз ми припускаємо, що поверхня рідини знаходиться на глибині 0, так що якщо дно пластини 3 футів під поверхнею, ми маємо$a=-3$. До цього ми повернемося пізніше.) Розбиваємо інтервал$[a,b]$ на$n$ підінтервали

$$a = y_1 < y_2 < \cdots <y_{n+1} = b,$$

з$i\,^\text{th}$ підінтервалом, що має довжину$\Delta y_i$. Сила, що$F_i$ чиниться на пластину в$i\,^\text{th}$ субінтервалі, дорівнює$F_i = \text{Pressure}\times \text{Area}.$

Тиск - глибина$\times w$. Ми наближаємо глибину цієї тонкої смуги, вибираючи$d_i$ будь-яке значення в$[y_i,y_{i+1}]$; глибина приблизно$-d_i$. (Наша конвенція$d_i$ має негативне число,$-d_i$ так і позитивне.) Для зручності ми дозволяємо$d_i$ бути кінцевою точкою підінтервалу; ми дозволяємо$d_i = y_i$.

Площа тонкої смужки приблизно довжина$\times$ ширини. Ширина - це$\Delta y_i$. Довжина є функцією деякого$y$ -значення$c_i$ в$i\,^\text{th}$ підінтервалі. Ми заявляємо, що довжина є$\ell(c_i)$. Таким чином

\ [\ begin {align*}
F_i &=\ текст {Тиск}\ раз\ текст {Площа}\\
&= -y_i\ cdot w\ times\ ell (c_i)\ cdot\ Дельта y_i.
\ end {align*}\]

Щоб наблизити загальну силу, складаємо приблизні сили на кожну з$n$ тонких смужок:

$$F = \sum_{i=1}^n F_i \approx \sum_{i=1}^n -w\cdot y_i\cdot\ell(c_i)\cdot\Delta y_i.$$

Це, звичайно ж, ще один Ріман Сум. Ми можемо знайти точну силу, взявши межу, оскільки підінтервальні довжини йдуть до 0; ми оцінюємо цю межу з певним інтегралом.

Ключова ідея 30: сила рідини на вертикально орієнтованій пластині

Нехай вертикально орієнтована пластина буде занурена в рідину з щільністю ваги,$w$ де верхня частина пластини знаходиться в,$y=b$ а внизу знаходиться в$y=a$. $\ell(y)$Дозволяти довжина пластини в$y$.

1. Якщо$y=0$ відповідає поверхні рідини, то сила, що чиниться на тарілку рідиною, дорівнює $$F=\int_a^b w\cdot(-y)\cdot\ell(y) dy.$$
2. Загалом, нехай$d(y)$ представляють відстань між поверхнею рідини і пластини в$y$. Тоді сила, що чиниться на тарілку рідиною, становить

$$F=\int_a^b w\cdot d(y)\cdot\ell(y)\ dy.$$

Приклад$\PageIndex{2}$: Finding fluid force

Розглянемо тонку пластину у формі рівнобедреного трикутника, як показано на малюнку,$\PageIndex{4}$ занурену у воду з ваговою щільністю 62,4 фунт/фут$^3$. Якщо дно пластини знаходиться на 10 футів нижче поверхні води, яка загальна сила рідини, що чиниться на цю пластину?

Малюнок$\PageIndex{4}$: Тонка пластинка у формі рівнобедреного трикутника в прикладі 7.6.2.

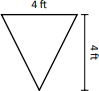
Рішення

Ми підходимо до цієї проблеми двома різними способами, щоб проілюструвати різні способи реалізації Key Idea 30. Спочатку дозволимо$y=0$ представляти поверхню води, потім розглянемо альтернативну умовність.

Малюнок$\PageIndex{5}$: Ескіз трикутної пластини в прикладі 7.6.2 з умовою, що рівень води знаходиться на рівні y = 0.

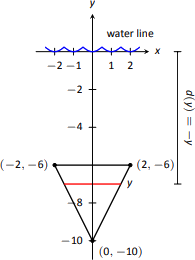
1. Ми дозволяємо$y=0$ представляти поверхню води; тому дно пластини знаходиться в$y=-10$. Центруємо трикутник на$y$ -осі, як показано на малюнку$\PageIndex{5}$. Глибина плити на$y$$-y$ вказана ключовою ідеєю. Розглянемо тепер довжину пластини в$y$.
   
   Нам потрібно знайти рівняння лівого і правого країв пластини. Права сторона - це лінія, яка з'єднує точки$(0,-10)$ і$(2,-6)$: ця лінія має рівняння$x=1/2(y+10)$. (Знайти рівняння в знайомому$y=mx+b$ форматі і вирішити для$x$.) Аналогічно і ліву сторону описує рядок$x=-1/2(y+10)$. Загальна довжина - це відстань між цими двома$\ell(y)=1/2(y+10) - (-1/2(y+10)) = y+10.$
   
   лініями: Загальна сила рідини тоді $$\begin{align*}F &= \int_{-10}^{-6} 62.4(-y)(y+10) dy \\ &= 62.4\cdot \frac{176}{3} \approx 3660.8\text{ lb}.\end{align*}$$
2. Іноді здається простіше зорієнтувати тонку пластину ближче до походження. Наприклад, розглянемо умовність про те, що дно трикутної пластини знаходиться на$(0,0)$, як показано на малюнку$\PageIndex{6}$. Рівняння лівої і правої сторін знайти нескладно. Вони$y=2x$ і$y=-2x$, відповідно, які ми переписуємо як$x= 1/2y$ і$x=-1/2y$. Таким чином, функція довжини є$\ell(y) = 1/2y-(-1/2y) = y$.
   
   Оскільки поверхня води знаходиться на 10 футів над основою плити, ми маємо, що поверхня води знаходиться на$y=10$. Таким чином функція глибини - це відстань між$y=10$ і$y$;$d(y) = 10-y$. Обчислюємо загальну силу рідини так: $$\begin{align*}F &=\int_0^4 62.4(10-y)(y)\ dy \\ &\approx 3660.8\text{ lb}.\end{align*}$$

Малюнок$\PageIndex{6}$: Ескіз трикутної пластини в прикладі 7.6.2 з умовністю про те, що основа трикутника знаходиться на$(0,0)$.

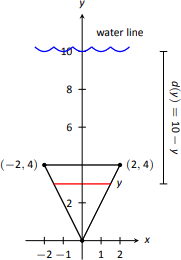
Правильна відповідь, звичайно, не залежить від розміщення пластини в координатній площині до тих пір, поки ми послідовні.

Приклад$\PageIndex{3}$: Finding fluid force

Знайдіть загальну силу рідини на дверях автомобіля, занурених до нижньої частини вікна у воду, де двері автомобіля - прямокутник довжиною 40 дюймів і висотою 27 дюймів (виходячи з розмірів Fiat Grande Punto 2005 року).

Рішення

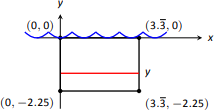
Двері автомобіля, як прямокутник, намальована на малюнку$\PageIndex{7}$. Його довжина -$10/3$ фути, а висота - 2,25 фута. Ми приймаємо конвенцію про те, що верхня частина дверей знаходиться на поверхні води, обидві з яких знаходяться на$y=0$. Використовуючи вагову щільність води 62,4 фунт/фут$^3$, ми маємо загальну силу як

\ [\ почати {вирівнювати*}
F &=\ int_ {-2.25} ^0 62,4 (-y) 10/3 день\\
&=\ int_ {-2.25} ^0 -208y dy\\
&= -104y^2\ Big|_ {-2.25} ^0\\
&= 526,5\ текст {фунт}
\ end {вирівнювати*}\]

Більшості дорослих було б дуже важко застосувати понад 500 фунтів сили до дверей автомобіля, сидячи всередині, що робить двері фактично неможливим для відкриття. Це суперечить інтуїтивності, оскільки більшість припускають, що двері було б відносно легко відкрити. Правда полягає в тому, що це не так, отже, поради щодо виживання, згадані на початку цього розділу.

Малюнок$\PageIndex{7}$: Ескіз занурених дверей автомобіля в прикладі 7.6.2.

Приклад$\PageIndex{4}$: Finding fluid force

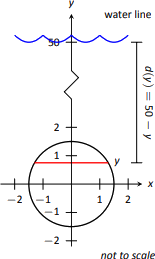
Будується підводна оглядова вежа з кільцевими оглядовими ілюмінатори, що дозволяють відвідувачам побачити підводне життя. Кожен вертикально орієнтований ілюмінатор повинен мати діаметр 3 футів, центр якого повинен бути розташований 50 футів під водою. Знайдіть загальну силу рідини, що чиниться на кожен ілюмінатор. Крім того, обчислити силу рідини на горизонтально орієнтованому ілюмінаторі, який знаходиться під 50 футів води.

Малюнок$\PageIndex{8}$: Вимірювання сили рідини на підводному ілюмінаторі в прикладі 7.6.4.

Рішення

Ми розміщуємо центр ілюмінатора біля початку, тобто поверхня води знаходиться на$y=50$ і функція глибини буде$d(y)=50-y$; див$\PageIndex{8}$. Рис.

Рівняння кола з радіусом 1,5 є$x^2+y^2=2.25$; рішення для$x$ нас є$x=\pm \sqrt{2.25-y^2}$, де позитивний квадратний корінь відповідає правій стороні кола, а негативний квадратний корінь відповідає лівій стороні кола. Таким чином, функція довжини на глибині$y$ є$\ell(y) = 2\sqrt{2.25-y^2}$. Інтеграція на$[-1.5,1.5]$ нас є:

\ [\ почати {вирівнювати*}
F &= 62.4\ int_ {-1.5} ^ {1.5} 2 (50-й)\ sqrt {2.25-y^2} ду\\
&= 62,4\ int_ {-1.5} ^ {1,5}\ великий (100\ sqrt {2.25-y^2} - 2y\ sqrt {2.25-y^2}\ великий) dy\\
&= 6240\ int_ {-1.5} ^ {1.5}\ великий (\ sqrt {2.25-y^2}\ великий) dy - 62,4\ int_ {-1.5} ^ {1.5}\ великий (2y\ sqrt {2.25-y^2}\ великий 2) день. \\
\ кінець {вирівнювати*}\]

Другий інтеграл вище можна оцінити за допомогою підстановки. Нехай$u=2.25-y^2$ с$du = -2y\,dy$. Нові межі:$u(-1.5)=0$ і$u(1.5)=0$; новий інтеграл буде інтегруватися від$u=0$ до$u=0$, отже, інтеграл дорівнює 0.

Перший інтеграл вище знаходить площу половини кола радіусом 1,5, таким чином, перший інтеграл оцінюється до$6240\cdot\pi\cdot1.5^2/2 = 22,054$. Таким чином, загальна сила рідини на вертикально орієнтованому ілюмінаторі становить$22,054$ фунт.

Знайти силу на горизонтально орієнтованому ілюмінаторі простіше: $$F =\ text {Pressure}\ times\ text {Area} = 62.4\ cdot50\ times\ pi\ cdot1.5^2 = 22,054\ text {lb} .$$ Що ці дві сили рівні не випадково; виявляється, що сила рідини, прикладена до вертикально орієнтованої окружності, центр якої знаходиться на глибині$d$ така ж, як сила, прикладена до горизонтально орієнтованого кола на глибині$d$.

Ми закінчуємо цю главу нагадуванням про справжні навички, які мають бути розроблені тут. Ми насправді не стурбовані здатністю знаходити сили рідини або обсяги твердих тіл обертання. Робота, виконана змінною силою, важлива, хоча вимірювання роботи, виконаної при натягуванні мотузки вгору скелі, ймовірно, не є.

Те, що ми насправді стурбовані, - це здатність вирішувати певні проблеми, спочатку наближаючи рішення, потім уточнюючи наближення, а потім визнання, якщо/коли цей процес уточнення призводить до певного інтегралу через межу. Знання формул, знайдених всередині спеціальних полів у цій главі, корисно, оскільки це допомагає вирішувати проблеми, знайдені у вправах, а інші математичні навички зміцнюються правильним застосуванням цих формул. Однак, що ще важливіше, зрозуміти, як була побудована кожна з цих формул. Кожен є результатом підсумовування наближень; кожне підсумовування було сумою Рімана, що дозволяє нам взяти межу і знайти точну відповідь через певний інтеграл.

Наступна глава стосується зовсім іншої теми: послідовності та серії. Коротше кажучи, послідовність - це список чисел, де ряд - це підсумовування списку чисел. Ці, здавалося б, прості ідеї призводять до дуже потужної математики.

Дописувачі та атрибуція

• Template:ContribApexCalc