6.1: Додавання та віднімання
- Page ID
- 67125
Вам знадобляться: Позитивні та негативні лічильники (Матеріальні карти 18A і 18B)
Пам'ятайте, що цілі числа складаються з нуля і рахункових чисел: 0, 1, 2, 3, 4, 5,. Коли школярі вперше бачать числовий рядок, вони зазвичай зосереджуються на цілих числах, і числовий рядок виглядає приблизно так:
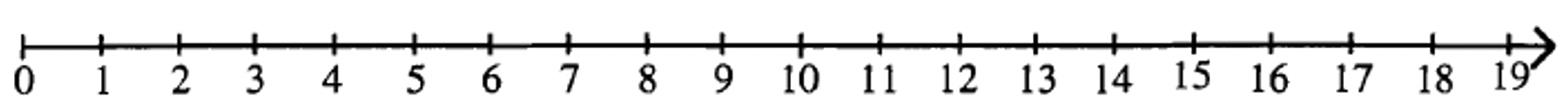
У цій моделі числовий рядок починається з нуля, а стрілка вправо вказує на те, що вона йде на невизначений термін вправо. Насправді, є нескінченно багато чисел (або точок) між будь-якими двома числами на числовій лінії. Наприклад, декілька з нескінченної кількості точок від 1 до 2 - це 3/2, 4/3, 5/4, 6/5, 7/5, 8/5 тощо На числовій лінії також є нескінченно багато ірраціональних чисел. Ірраціональні числа не можна записати як співвідношення двох цілих чисел, подібно до того, як ми представляємо скорочені дроби. Прикладами деяких ірраціональних чисел між 3 і 4 є\(\sqrt{11}\)\(\sqrt{15}\),, 3.10110111..., і\(\pi\). Всупереч поширеній думці,\(\pi\) не дорівнює 3,14 і\(\pi\). не дорівнює 22/7. І 3,14, і 22/7 є раціональними числами (на відміну від\(\pi\) яких є ірраціональним числом, НЕ раціональним числом), а 3,14 і 22/7 є лише наближеннями, які зазвичай використовуються при обчисленні с\(\pi\). Ірраціональні числа будуть вивчені і розглянуті більш детально в іншому модулі.
Гаразд, давайте повернемося до нашого обговорення числового рядка. Числовий рядок, показаний на початку цього набору вправ, насправді є лише половиною рядка, так що називати його числовим рядком дійсно неправильно. Горизонтальна лінія йде нескінченно як в лівому, так і в правому напрямку, а не тільки вправо. Числа праворуч від нуля називаються додатними числами. Числа зліва від нуля називаються від'ємними числами. Нуль — єдине число, яке не має знака — воно не є ні позитивним, ні негативним. Для кожного додатного числа існує відповідне від'ємне число, яке на заданому числовому рядку дорівнює відстані від нуля, що і додатне число, але воно знаходиться зліва від нуля. Числа на однаковій відстані від нуля, але з протилежних сторін називаються «протилежностями». Негативні числа представлені так: -5 читається «негативна п'ятірка», -20 читається «негативна двадцятка» і т.д. так, 5 і -5 - протилежності, 20 і -20 - протилежності, а нуль - протилежність собі.
Для кожної позначки на цифровому рядку заповніть відсутні цифри
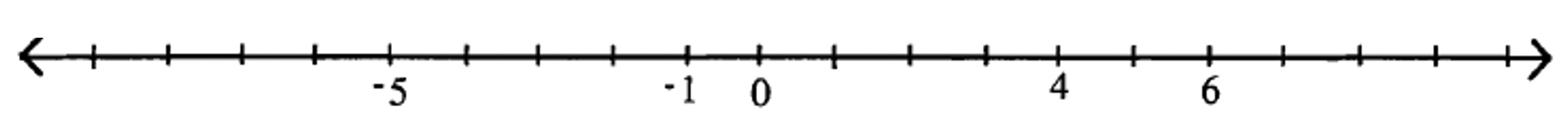
Визначення: Набір натуральних чисел (які також прийнято називати натуральними числами або числами підрахунку) записується як: {1, 2, 3, 4,...}. Позитивні числа також можуть бути записані з позитивним знаком перед ним. Наприклад, 4 може бути написано +4.
Безліч цілих чисел містить як нуль, так і натуральні числа і записується як: {0, 1, 2, 3,...}.
Означення: Безліч від'ємних цілих чисел містить точно всі протилежності всіх натуральних чисел.
1. Запишіть множину від'ємних цілих чисел:
Означення: Безліч цілих чисел складається з нуля, натуральних чисел і від'ємних цілих чисел.
2. Запишіть безліч цілих чисел:
Означення: Абсолютне значення числа на числовій лінії визначається як відстань, що точка знаходиться від нуля. Оскільки абсолютне значення визначається з точки зору відстані, воно ніколи не може бути негативним. Щоб оцінити абсолютне значення числа, вкажіть відстань, яке воно знаходиться від нуля.
Абсолютне значення 5 дорівнює 5, так як відстань від 5 до 0 дорівнює 5 одиницям. Абсолютне значення -5 також дорівнює 5, так як відстань від -5 до 0 також становить 5 одиниць.
Оцініть абсолютне значення кожного з наступних чисел:
| а. 4: ____ | б. -8: ____ | c. 2: ____ | д. -1: ____ | е. 0: ____ |
Для позначення абсолютного значення числа укладемо його між двома вертикальними лініями. «Абсолютне значення -15 дорівнює 15» пишеться так: | -15 | = 15. Щоб спростити задачу зі знаком абсолютного значення, спочатку потрібно спростити частину всередині знака абсолютного значення. Отже, якщо частина всередині знака абсолютного значення не просто числівник, подумайте про частину всередині як про те, що знаходиться в дужках, і спростіть її спочатку. Потім візьміть абсолютне значення числівника. Ви повинні будете зробити це для частини c і f вправи 4.
Спростіть кожне з наступних дій:
| а. | 7 | = ______ | в. | 7 — 3 | = _______ | |
| д.\(|\frac{3}{7}|\) = ______ | е.\(|-\frac{3}{7}|\) = ______ | ф. | 2\(\cdot\) 5 — 4 | = _______ |
Напишіть два числівники, які мають абсолютне значення 6 ______ і _______
Напишіть два числівники, які мають абсолютне значення 19 ______ і ______
Запишіть всі числівники, які мають абсолютне значення нуль _______
Запишіть всі числівники, які мають абсолютне значення -10 (від'ємне 10) _______
Кожне додатне і від'ємне число може бути представлено спрямованим відрізком лінії, який називається вектором.
В основному вектор виглядає як стрілка. Він має дві властивості: має певну довжину (звану «величиною») і вказує в певному напрямку. Оскільки ми будемо використовувати горизонтальні числові лінії, ми будемо малювати горизонтальні вектори. Стрілка, що вказує вправо, буде позначати позитивне число, а стрілка, що вказує вліво, - негативне число.
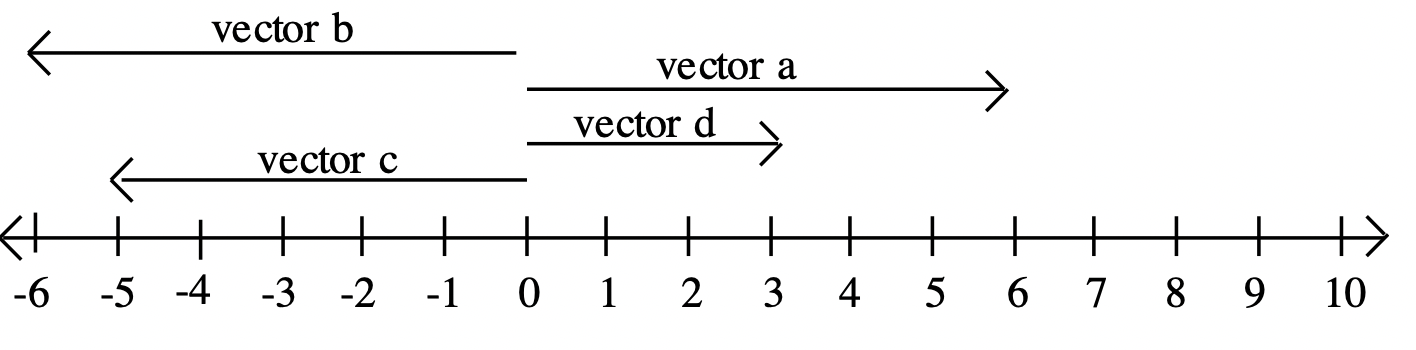
Нижче наведено числовий рядок з деякими векторами, показаними вище. Вектор a має довжину 6 одиниць і стрілка вказує вправо. Тому вона являє собою число +6. Вектор b також має довжину 6 одиниць, але він вказує ліворуч. Тому вона являє собою число -6. Обидва вектори мають величину 6.

- Яке число представляє вектор c? _________
- Яке число представляє вектор d? _________
Кожен вектор має початкову точку (початкову точку вектора) і кінцеву точку (кінцеву точку, де показана стрілка). Якщо початкова точка вектора розміщена на нулі, числову лінію можна використовувати як зручний маркер — кінцева точка вектора просто розміщується на представленому числі. Але не потрібно представляти його таким чином, як ви могли бачити з усіх векторів, показаних у вищезазначених прикладах. Вектори a, b, c і d могли бути намальовані з початковою точкою на нулі, як показано нижче. Якщо ви намалюєте вектор з початковою точкою на нулі, число, яке представляє вектор, є просто тим самим числом на числовій лінії, де знаходиться його кінцева точка.
Інший спосіб мислення про цифри - думати про них з точки зору «дій». Ви можете думати про цифру «5» як дію переміщення 5 пробілів вправо. Коли ви малюєте вектор, що представляє 5, це спосіб показати цю конкретну дію. Ви можете думати про число «-3" як дію переміщення 3 пробілів вліво. Коли ви малюєте вектор, що представляє -3, це спосіб показати цю конкретну дію.
Числова лінія, поряд з цією ідеєю мислення про числа з точки зору дій, може бути використана для складання чисел разом.
Визначення: Щоб додати два числа, m і n, ви ВИКОНАЄТЕ першу дію, m Знак додавання означає NOW DO другу дію, n. Відповіддю на задачу (яка є сумою: m + n) є єдиною дією, яка могла бути виконана для досягнення того ж результату, що і виконання окремих дій у спадкоємство.
Розглянемо цей практичний спосіб мислення про нього. Подумайте про ходьбу на схід як позитивне число, а ходьба на захід - як негативне число. Якщо ви йшли 5 блоків на схід, потім 7 кварталів на захід, потім 3 квартали на схід, ви б один блок на схід від початкової відправної точки. Це може бути спосіб подумати над проблемою: 5 + (-7) + 3 = 1.
- Виберіть початкову точку і намалюйте вектор m (який є способом представлення дії m) з його початковою точкою у зазначеній початковій точці.
- Знак додавання означає початок з кінцевої точки попередньої дії DO наступної дії. Отже, малюємо вектор n, помістивши початкову точку n в кінцевій точці вектора m.
- Сума, m + n, - це те саме число, яке буде представлено вектором з початковою точкою, розміщеною на початковій початковій точці та кінцевою точкою на кінцевій кінцевій кінцевій точці після останньої дії.
Тільки для ЗРУЧНОСТІ найпростіше завжди використовувати числовий рядок і вибрати нуль як початкову точку початку. Роблячи це, відповідь на проблему буде там, де кінцева точка останньої дії приземлилася на числовому рядку.
Перш ніж йти далі, важливо відзначити, що не обов'язково відзначати кожну точку на числовій лінії. Насправді це неможливо, оскільки на числовій лінії нескінченно багато точок. Однак зазвичай є гарною ідеєю позначити нуль і принаймні одну точку по обидва боки нуля. Відзначте цифровий рядок таким чином, щоб було зручно виконувати завдання.
Ми скористаємося вищевказаною процедурою, щоб додати наступні цифри. Для цих прикладів і для вправ почніть з нуля для зручності. Намалюйте перший вектор. Потім трохи підніміться вгору, щоб намалювати другий вектор, щоб було очевидно, який вектор був намальований першим, а який був намальований останнім. Для кожного числа в сумі має бути один вектор. Оскільки ми ставимо початкову точку першого вектора на нуль, ми можемо констатувати відповідь, зазначивши, де кінцева точка останнього вектора приземлилася на числовій лінії.
4 + 2.
Рішення
Починаючи з нуля, ВИКОНАЙТЕ дію 4 (яке показано малюванням вектора, що представляє 4), потім, починаючи з точки, де закінчилося перша дія, ВИКОНАЙТЕ дію 2 (показано малюванням вектора, що представляє 2).
Відповідь - 6, оскільки кінцева точка останнього вектора приземлилася на 6.
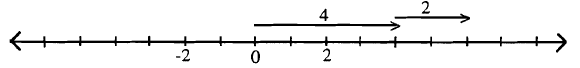
-5 + 3.
Рішення
Починаючи з нуля, ВИКОНАЙТЕ дію -5 (що показано малюванням вектора, що представляє -5), потім ВИКОНАЙТЕ дію 3 (показано малюванням вектора, що представляє 3).
Відповідь -2, оскільки кінцева точка останнього вектора приземлилася на -2.
-3 + -4.
Рішення
Починаючи з нуля, виконайте дію -3 (показано малюванням вектора, що представляє -3), потім ВИКОНАЙТЕ дію -4 (показано малюванням вектора, що представляє -4).
Відповідь -7, оскільки кінцева точка останнього вектора приземлилася на -7.
-4 + 8.
Рішення
Починаючи з нуля, ВИКОНАЙТЕ дію -4 (що показано малюванням вектора, що представляє -4), потім ВИКОНАЙТЕ дію 8 (показано малюванням вектора, що представляє 8).
Відповідь 4, оскільки кінцева точка останнього вектора приземлилася на 4.
50 + -35.
Починаючи з нуля, виконайте дію 50 (показано малюванням вектора, що представляє 50), потім ВИКОНАЙТЕ дію -35 (показано малюванням вектора, що представляє -35).
Відповідь 15, оскільки кінцева точка останнього вектора приземлилася на 15.

ВКРАЙ ВАЖЛИВО, щоб ви ПОЗНАЧИЛИ свій номер рядка. В іншому випадку незрозуміло, що являє собою кожен вектор. Не варто вважати, що кожна позначка стоїть на 1 одиниці. Без мітки принаймні одного числа на кожній стороні нуля в останньому прикладі можна припустити, що останній показаний приклад представляв 10 + -7 і що відповідь була 3.
Використовуйте вектори на числовому рядку, щоб скласти наступні числа разом. Позначте та позначте свою цифру з принаймні нулем та точкою з обох боків.
Ось приклад того, як робити такі проблеми:
-4 + 8 + (-5) = -1, оскільки кінцева точка останнього вектора приземлилася на -1.

|
а. 5 + (-8) = _____ з ______________________________________________ 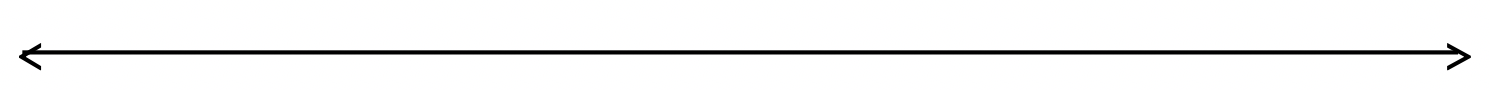 |
|
б. -7 + (-2) = _____ з _____________________________________________ 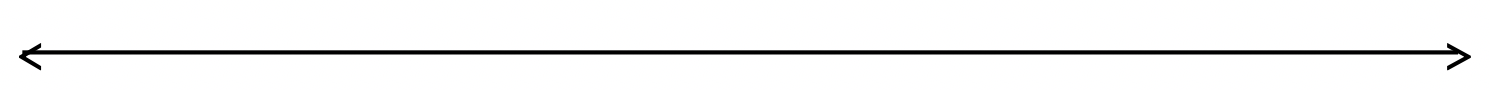 |
|
c. -5 + 9 = _____ з _____________________________________________ 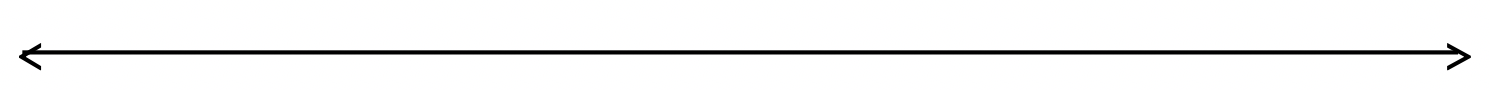 |
|
д. 7 + (-6) = _____ з ______________________________________________ 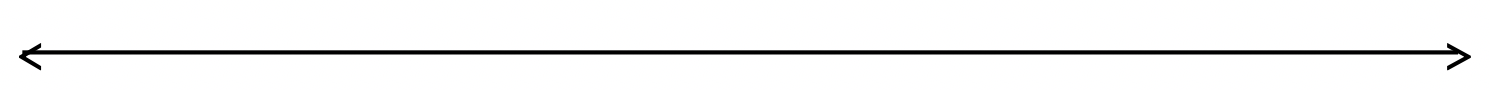 |
|
е. -7 + 5 = _____ з __________________________________________________ 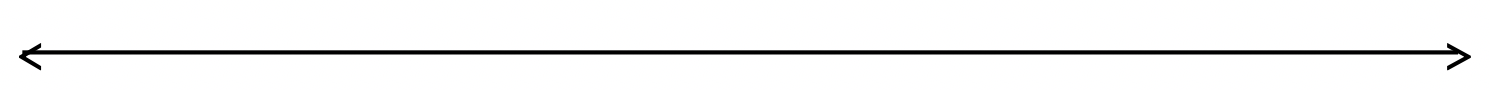 |
|
ф. -100 + 40 = _____ з ______________________________________________ 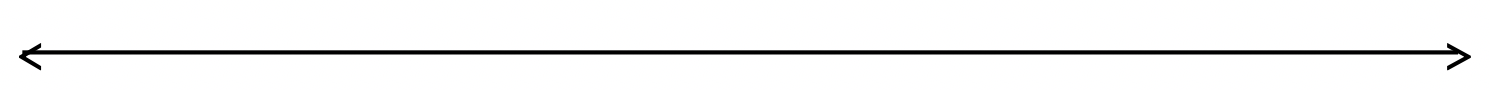 |
|
г. -3 + (-2) + 4 = _____ з ___________________________________________ 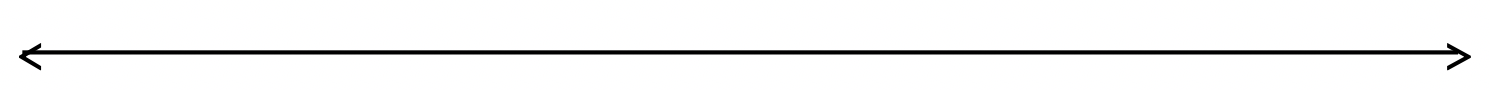 |
|
ч. 4 + (-12) + 5 = _____ з __________________________________________________ 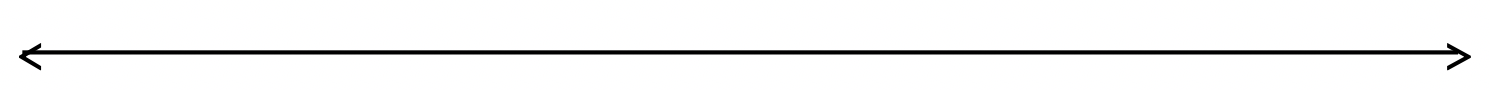 |
Іноді ви побачите вертикальні числові лінії замість горизонтальних числових ліній. При цьому позитивні числа йдуть вгору, і представляються вертикальними векторами зі стрілкою вгору. Так само від'ємні числа опускаються вниз і представлені вертикальними векторами, спрямованими вниз. Приклад вертикальної цифрової лінії показаний праворуч.
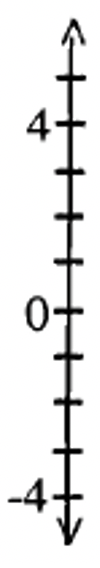
Існує загальне використання використання вертикальної цифрової лінії. Ви можете придумати один? Подивіться, якщо ви можете придумати будь-який і запишіть тут.
Якщо вам потрібна підказка для вправи 11, подумайте про погоду.
Ми будемо продовжувати думати про дії, коли ми використовуємо вектори для виконання завдань віднімання.
Визначення: Щоб відняти число, m, ви скасуєте дію, m що означає, що ви РОБИТЕ ПРОТИЛЕЖНІСТЬ дії m.
Незалежно від того, чи робите ви проблему віднімання, проблему додавання або обидва в одній задачі, відповідь на проблему - це єдина дія, яку можна було б зробити для досягнення того ж результату, що і виконання окремих дій послідовно.
Ви можете думати про віднімання як скасування деякої помилки.
Розглянемо варіацію на оригінальному прикладі, наданому для додавання. Щоб освіжити вашу пам'ять, ось така проблема: Подумайте про ходьбу на схід як позитивне число, а ходьба на захід - як негативне число. Якщо ви йшли 5 блоків на схід, потім 7 кварталів на захід, потім 3 квартали на схід, ви б один блок на схід від початкової відправної точки. Це може бути спосіб подумати над проблемою: 5 + (-7) + 3 = 1.
Уявіть, що ви йшли 5 кварталів на схід, потім 2 квартали на захід, а потім зрозуміли, що ви зробили помилку. Ви не повинні були ходити 2 квартали на захід. Вам потрібно буде скасувати цю помилку. Що б ви зробили, щоб скасувати цю помилку і повернутися туди, де ви були, перш ніж ви йшли 2 квартали на захід від аварії?
У вправі 12, я сподіваюся, ви зрозуміли, що вам потрібно пройти 2 блоки на схід, щоб скасувати свою помилку. Щоб перевести кроки, зроблені в #12, ми могли б написати 5 + (-2) — (-2) = 5. Ось як ми пояснюємо і показуємо дії за допомогою векторів на числовому рядку.
5 + (-2) — (-2): Починаючи з нуля, ВИКОНАЙТЕ дію 5 (показано малюванням вектора, що представляє 5), потім ВИКОНАЙТЕ дію -2 (показано малюванням вектора, що представляє -2), потім скасуйте дію -2 (що означає ЗРОБИТИ ПРОТИЛЕЖНІСТЬ дії -2, яка полягає у виконанні дії +2, показано малюванням вектора, що представляє +2).
Відповідь дорівнює 5, оскільки кінцева точка останнього вектора приземлилася на 5.

Порядок використання векторів для додавання або віднімання двох чисел:
- Якщо перше число дорівнює m, виберіть початкову точку і намалюйте вектор m (який є способом представлення дії m) з його початковою точкою у вказаній початковій точці.
- Якщо наступний знак - додавання, виконайте наступну дію, намалювавши вектор, що представляє наступне число, розмістивши початкову точку цього вектора в кінцевій точці попереднього вектора. Якщо, з іншого боку, наступним знаком є віднімання, скасуйте наступну дію. Отже, намалюйте вектор, що представляє протилежний наступному числу, помістивши початкову точку цього вектора в кінцевій точці попереднього вектора.
- Якщо є інший знак додавання або віднімання, поверніться до кроку 2. В іншому випадку на цьому етапі ми можемо знайти відповідь. Відповідь - це те саме число, яке було б представлено вектором із початковою точкою, розміщеною на початковій початковій точці та кінцевою точкою на кінцевій кінцевій кінцевій точці після останньої дії.
Знову ж таки, використовувати нуль як початкову точку ЗРУЧНО, оскільки відповідь на проблему буде там, де кінцева точка останньої дії приземлилася на числовому рядку.
Ми будемо використовувати вищевказану процедуру для обчислення наступних проблем. Для цих прикладів і для вправ почніть з нуля для зручності. Намалюйте перший вектор. Потім трохи підніміться вгору, щоб намалювати другий вектор, щоб було очевидно, який вектор був намальований першим, а який був намальований останнім. Для кожного числа у задачі має бути один вектор. Оскільки ми ставимо початкову точку першого вектора на нуль, ми можемо констатувати відповідь, зазначивши, де кінцева точка останнього вектора приземлилася на числовій лінії.
4 — (-2).
Рішення
Починаючи з нуля, ВИКОНАЙТЕ дію 4 (що показано малюванням вектора, що представляє 4), потім СКАСУВАТИ дію -2 (що означає ЗРОБИТИ ПРОТИЛЕЖНЕ дії -2, тобто зробити дію +2, показану малюванням вектора, що представляє +2).
Відповідь - 6, оскільки кінцева точка останнього вектора приземлилася на 6.
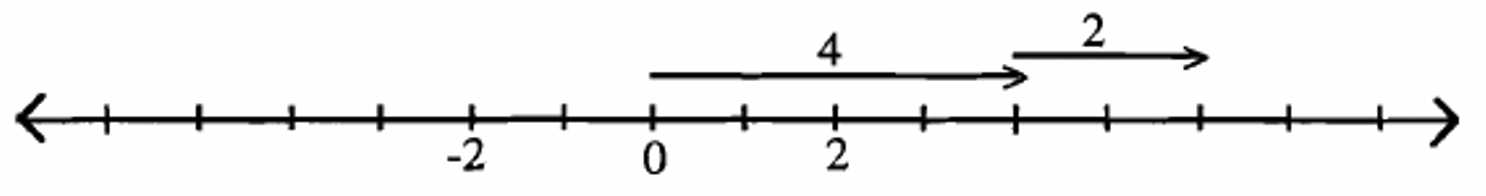
-5 — (-3).
Рішення
Починаючи з нуля, ВИКОНАЙТЕ дію -5 (показано малюванням вектора, що представляє -5), потім СКАСУВАТИ дію -3 (що означає ЗРОБИТИ ПРОТИЛЕЖНІСТЬ дії -3, тобто ВИКОНАТИ дію +3, показану малюванням вектора, що представляє +3).
Відповідь -2, оскільки кінцева точка останнього вектора приземлилася на -2.
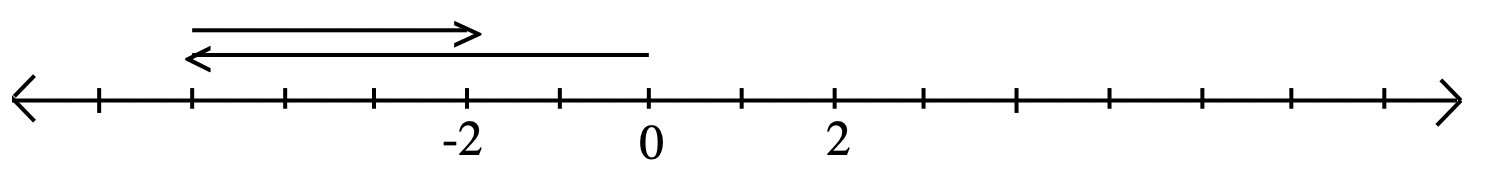
-3 — (+4).
Рішення
Починаючи з нуля, ВИКОНАЙТЕ дію -3 (показано малюванням вектора, що представляє -3), потім СКАСУВАТИ дію +4 (що означає ЗРОБИТИ ПРОТИЛЕЖНІСТЬ дії +4, тобто ВИКОНАТИ дію -4, показану малюванням вектора, що представляє -4).
Відповідь -7, оскільки кінцева точка останнього вектора приземлилася на -7.

-4 — (-8).
Рішення
Починаючи з нуля, ВИКОНАЙТЕ дію -4 (показано малюванням вектора, що представляє -4), потім скасуйте дію -8 (що означає ЗРОБИТИ ПРОТИЛЕЖНЕ дії -8, тобто зробити дію +8, показану малюванням вектора, що представляє +8).
Відповідь 4, оскільки кінцева точка останнього вектора приземлилася на 4.

50 + (-35).
Рішення
Починаючи з нуля, виконайте дію 50 (показано малюванням вектора, що представляє 50), потім ВИКОНАЙТЕ дію -35 (показано малюванням вектора, що представляє -35).
Відповідь 15, оскільки кінцева точка останнього вектора приземлилася на 15.
ВКРАЙ ВАЖЛИВО, щоб ви ПОЗНАЧИЛИ свій номер рядка. В іншому випадку незрозуміло, що являє собою кожен вектор. Не варто вважати, що кожна позначка стоїть на 1 одиниці. Без мітки принаймні одного числа на кожній стороні нуля в останньому прикладі можна припустити, що останній показаний приклад представляв 10 + (-7) і що відповідь була 3.
Використовуйте вектори на числовому рядку, щоб скласти наступні числа разом. Позначте та позначте свою цифру з принаймні нулем та точкою з обох боків.
Ось приклад того, як робити такі проблеми:
-4 + 8 + (-5) = -1, оскільки кінцева точка останнього вектора приземлилася на -1.

|
а. 5 — (+8) = _____ з __________________________________________.  |
|
б. -7 — (+2) = _____ з __________________________________________.  |
|
в. -5 — (-9) = _____ з _____________________________________________.  |
|
д. 7 — (+6) = _____ з __________________________________________.  |
|
е. -7 — (-5) = _____ з __________________________________________.  |
|
ф. -100 — (-40) = _____ з __________________________________________.  |
|
г. -3 — (+2) — (-4) = _____ з ______________________________________________.  |
|
ч. 4 — (+12) + 5 = _____ з __________________________________________.  |
На даний момент було б корисно, якби ви озирнулися на приклади на сторінках 4 і 5 і порівняли їх з останніми прикладами, показаними на сторінках 8 і 9. Приклади на сторінках 8 та 9 включають віднімання, тоді як приклади на сторінках 4 та 5 є проблемами додавання. Використовуючи ідею додавання та віднімання за допомогою векторів та підхід дії (або DO або UNDO дію), проблеми, виконані з векторами на числовій лінії, виглядають точно так само. Те ж саме вірно, якщо ви подивитеся на проблеми у вправах 10 і 13. Якось тоді здається зв'язок між відніманням і додаванням. Ми складемо все разом після того, як ми досліджуємо зовсім інший спосіб додавання та віднімання, на цей раз за допомогою маніпуляцій.
Іншим способом представлення позитивних і негативних чисел є використання колекції позитивних і негативних лічильників. Вам потрібно використовувати лічильники одного кольору для представлення позитивних чисел (кожен лічильник = +1) і лічильники іншого кольору для представлення негативних чисел. Якщо ви використовуєте матеріальні картки, кожен зелений квадрат буде представляти +1, а кожен червоний квадрат - -1. Ми виявимо, що існує багато способів представлення того ж числа за допомогою цих лічильників. Вийдіть з лічильників, щоб зробити наступні вправи.
Найпростіший спосіб представити додатне число, x, - це мати колекцію x зелених лічильників. Найпростіший спосіб представити від'ємне число, -y, - це мати колекцію y червоних лічильників. Наприклад, 4 червоні лічильники представлятимуть -4, а 3 зелених - +3. У цих вправах я іноді представляю позитивний лічильник або квадратом або колом з позитивним знаком (+) або «G» всередині, або просто «G». Аналогічно негативний лічильник буде представлений або квадратом або колом з негативним знаком (-) або «R» всередині, або просто «R».
Яке число представлено кожною з наступних колекцій?
|
а. 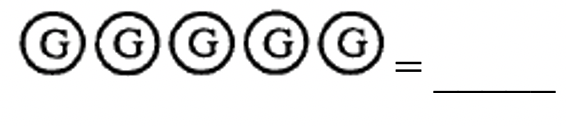 |
б РРРРРРР = ______ |
|
c. 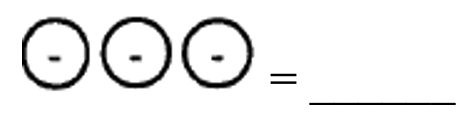 |
д. 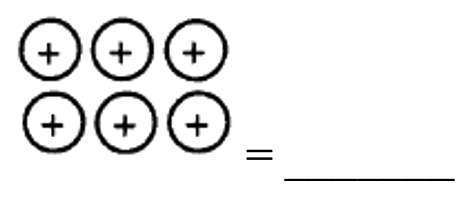 |
Під кожним номером уявити число, показуючи колекцію лічильників.
| б. 2 |
Вправа 16
Яке число, на вашу думку, представляє колекція нижче? ______ Поясніть чому.
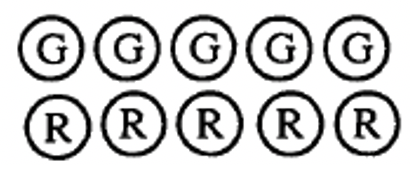
У вправі 14 було 5 позитивів і 5 негативів. Ви придумали відповідь нуль? Якщо так, то ви на правильному шляху. В основному, коли позитивний лічильник парний з негативним лічильником, вони зводять нанівець один одного. Кожен раз, коли існує така ж кількість позитивних лічильників, що і негативні лічильники, у вас є подання числа, нуль.
Використовуючи позитивні та негативні лічильники, покажіть три різних уявлення про нуль.
| а. | б. | c. |
Давайте подивимося, чи зможете ви розібратися, яке число представляє кожна колекція.
Вкажіть число, представлене кожною колекцією
|
a Наведена нижче колекція представляє _____ 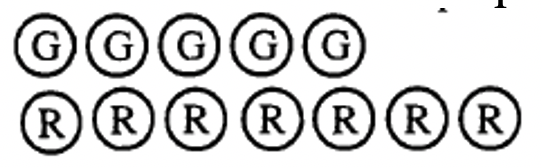 |
b Наведена нижче колекція представляє _____ 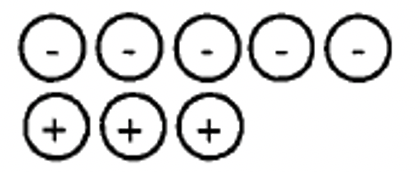 |
|
c Наведена нижче колекція представляє _____ 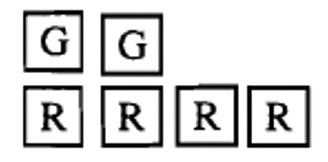 |
d Наведена нижче колекція представляє _____ 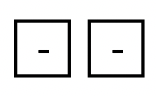 |
|
e Наведена нижче колекція представляє _____ RRRRRRGG |
f Наведена нижче колекція представляє _____ ГРГРГРРРРРГГГГГ |
|
g Наведена нижче колекція представляє _____ 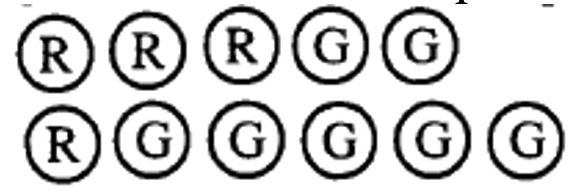 |
h Наведена нижче колекція представляє _____ 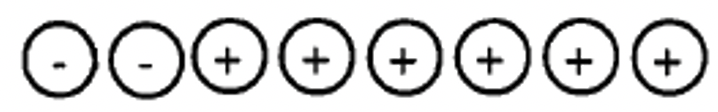 |
Як ви думаєте, ви це зробили? Сподіваюся, ви придумали відповідь -2 для а-д. Якщо так, то ви повинні переконатися, що різні колекції можуть представляти одне і те ж число. Кожне спарювання негативу з позитивом в основному «скасовує один одного». Тому, щоб з'ясувати, яке число представляє конкретна колекція, просто з'єднайте якомога більше позитивів з негативами (червоно-зелені пари), і видаліть або ігноруйте ці лічильники. Потім порахуйте лічильники того «кольору» або «знака», який залишився. Можливо, ви помітили, що було легше обчислити a-d, тому що пари були легше побачити.
Використовуючи позитивні і негативні лічильники, знайдіть 3 різних представлення 4. Зробіть це з вашими фактичними позитивними та негативними маніпуляціями в першу чергу. Потім покажіть його на папері.
| а. | б. | c. |
Використовуючи позитивні (зелені) і негативні (червоні) лічильники, показати 3 різних представлення -4. Потім покажіть три різні уявлення нижче.
| а. | б. | c. |
Давайте перейдемо до того, як ми можемо використовувати лічильники для додавання цілих чисел. Щоб додати цілі числа, просто створіть колекцію лічильників, що представляють кожне число, яке потрібно додати, і об'єднати лічильники. Потім знайдіть число, яке представляє отримана колекція. Зробіть це, спочатку спарюючи будь-які позитиви та негативи та видаливши їх з купи.
Показати два різних способи використання лічильників, щоб додати 4 + (-7).
Перший спосіб:
По-перше, об'єднайте колекцію, що представляє 4 (4G) і колекцію, що представляє -7 (7R):
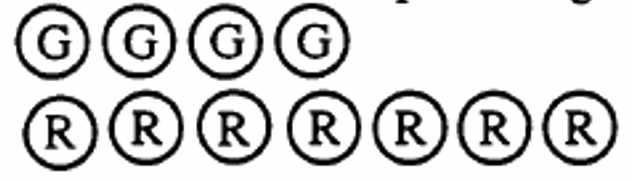
По-друге, видаліть будь-які червоно-зелені пари:
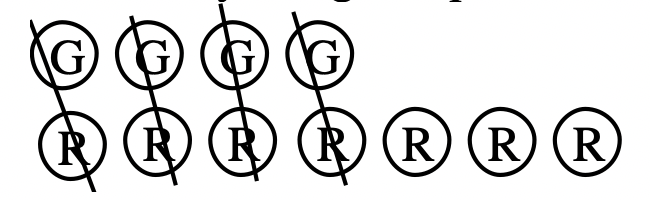
По-третє, порахуйте залишилися лічильники:
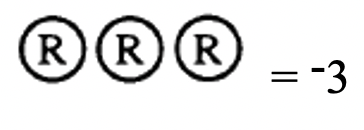
Тому 4 + (-7) = -3.
Другий спосіб:
Спочатку об'єднайте колекцію, що представляє 4 (8G та 4R) та колекцію, що представляє 7 (8R та 1G):
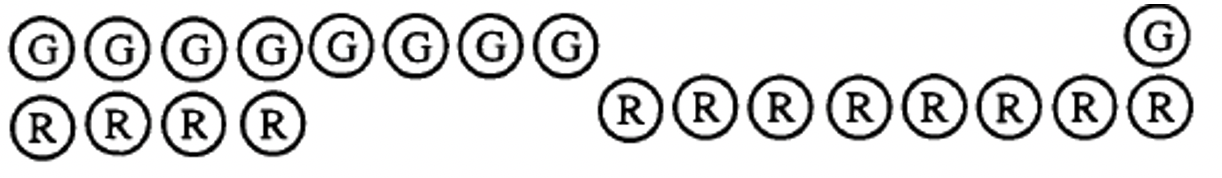
По-друге, видаліть будь-які червоно-зелені пари:
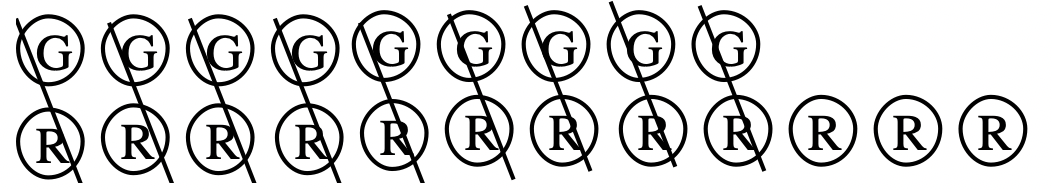
По-третє, порахуйте, які лічильники залишилися:

Тому 4 + (-7) = -3.
Звичайно, більш простий і прямий спосіб - це перший спосіб, але результат однаковий навіть тоді, коли на першому кроці використовуються складні уявлення чисел.
Використовуйте червоний і зелений лічильники, щоб додати наступні цілі числа. Виконуйте ці проблеми, використовуючи актуальні маніпулятори. Потім поясніть і покажіть кроки нижче
Хоча віднімання трохи складніше за допомогою лічильників, вони забезпечують дійсно цікавий спосіб показати, як віднімати негативні числа.
Використовуючи лічильники, m — n означає вилучити колекцію лічильників, що представляють n, із колекції лічильників, що представляють m. Число, яке представляє отримана колекція, є різницею (відповіддю).
Це означає, що ми повинні почати з колекції лічильників, що представляють m. Для того, щоб вилучити колекцію, що представляє n, має бути можливим вилучити колекцію, що представляє n, зі збірки, що використовується для m. Іноді початкової збірки, обраної для m, буде недостатньо, і колекцію потрібно змінити. додаючи кілька червоно-зелених пар до колекції, що представляє m. Зазвичай ми починаємо з простого представлення m лічильників і дивимося, чи можна видалити або забрати подання n лічильників. Якщо так, то робимо ніж і знаходимо число, яке представляє отримана колекція. Давайте спробуємо це на деяких прикладах, використовуючи фізичні моделі (маніпулятори), а потім потренуємося показувати це на папері.
4 — 2
Це означає вилучити збірку, що представляє 2, з колекції, що представляє 4.
Крок 1: Зробіть колекцію, що представляє 4 (4 зелених лічильника):\(\not{GG}\) GG
Крок 2: Вийміть колекцію, що представляє 2 (2 зелених лічильника):
Крок 3: Залишилася колекція (GG) представляє 2. Отже, 4 — 2 = 2.
-5 — (-3)
Це означає вилучити збірку, що представляє -3, з колекції, що представляє -5.
Крок 1: Зробіть колекцію, що представляє -5 (5 червоних лічильників): RRRRR
Крок 2: Вийміть колекцію, що представляє -3 (3 червоні лічильники):
Крок 3: Залишилася колекція (RR) представляє -2. Отже, -5 — (-3) = -2.
3 — 5
Це означає вилучити збірку, що представляє 5, з колекції, що представляє 3.
Крок 1: Зробіть колекцію, що представляє 3 (3 зелених лічильника): GGG
О НІ! Наступним кроком буде винести подання 5 (5 зелених лічильників), але помітити, що це неможливо, тому що є тільки 3 зелені лічильники для початку. Сюди потрібно вставити додатковий крок. Нам потрібно переробити уявлення 3, щоб можна було вийняти 5 зелені. Має сенс, що ми завжди можемо вставити деякі зелено-червоні пари до подання 3 (кожна зелено-червона пара є ефектом додавання нуля), не змінюючи подання 3. В даному прикладі має сенс додати ще 2 червоно-зелені пари, щоб в колекції було 5 зелених і 2 червоних. Це все одно буде колекція, що представляє 3. Цей додатковий крок часто необхідний при виконанні завдань віднімання з цілими числами.
Крок 2: Додайте 2 червоно-зелені пари до колекції, що представляє 3: GGGRGRG
Крок 3: Вийміть колекцію, що представляє 5 (5 зелених лічильників):\(\begin{aligned} & \fbox{GGGGG} \\ & \text{RR} \end{aligned}\)
Крок 4: Залишилася колекція (RR) представляє -2. Отже, 3 — 5 = -2
Для кожної задачі вкажіть, що означає проблема (Наприклад, 4 - (- 9) означає видалити колекцію лічильників, що представляють -9 з колекції лічильників, що представляють 4), а потім пояснити і показати кожен крок, який потрібно зробити, щоб знайти відповідь. Кожна проблема вимагає 3 або 4 кроків. Ви повинні робити ці проблеми за допомогою маніпуляцій, і, як ви це робите, пояснити і показати кроки на папері.
|
а. 6 — 3 Це означає Показати всі кроки нижче. |
|
б. 4 — 6 Це означає Показати всі кроки нижче. |
|
с. -7 — (- 6) Це означає Показати всі кроки нижче. |
|
д. -3 — (- 7) Це означає Показати всі кроки нижче. |
|
е. 4 — (- 3) Це означає Показати всі кроки нижче. |
|
ф. -2 — 5 Це означає Показати всі кроки нижче. |
|
г. 5 — 5 Це означає Показати всі кроки нижче. |
|
ч. 5 — (- 5) Це означає Показати всі кроки нижче. |
|
i. -4 — (- 4) Це означає Показати всі кроки нижче. |
|
дж. -6 — 6 Це означає Показати всі кроки нижче. |
Створіть, що означає проблема з точки зору використання позитивних і негативних лічильників і показати всі кроки, щоб (а) відняти 5 - 8, а потім (b) додати 5 + (-8).
| а. 5 — 8 |
| c Що ви помітили про свої відповіді на a і b? |
Сподіваємось, ви помітили, що видалення колекції, що представляє 8 з колекції, що представляє 5, призвело до того ж результату, що і об'єднання колекції, що представляє 5 та -8.
Іншими словами, віднімання 8 дало той же результат, що і додавання -8.
- Використовуйте фактичні маніпулятори. Почніть з колекції щонайменше 4 червоних і деяких зелених лічильників і напишіть, що у вас є нижче:
- Видаліть 4 червоні лічильники з вашої колекції. Покажіть цей крок, перекреслюючи або обводячи 4 червоні лічильники у вашій колекції вище. Після видалення цих червоних лічильників, який номер колекція частково а тепер представляє? ______
- Почніть спочатку. Почніть з об'єднання оригінальної колекції, яку ви мали в частині a, з 4 зеленими лічильниками (додайте 4 зелені лічильники до оригінальної колекції). Нижче покажіть, як виглядає колекція зараз.
- Яке число представляє ваша підсумкова колекція? ______
Вправи 21 і 22 ілюструють дуже важливий факт про віднімання. Віднімання числа дає той самий результат, що і додавання протилежного числа. Вправи 10 і 13, і приклади, що передують кожному з цих вправ, також проілюстрували цей факт.
Зверніть увагу, що червоні і зелені лічильники, або позитивні і негативні лічильники протилежні.
Поясніть, що означає 7 — 4, а потім викладіть інший спосіб отримати той же результат.
Рішення
7 - 4 означає видалити колекцію, що представляє 4 з колекції, що представляє 7. Це дає той самий результат, що і об'єднання колекції, що представляє 7, з колекцією, що представляє протилежну 4, тобто об'єднати колекцію, що представляє 7, з колекцією, що представляє -4 (що означає об'єднати 7G з 4R). Отже, 7 - 4 = 7 + (- 4).
Поясніть, що означає 2 — (- 6), а потім викладіть інший спосіб отримати той же результат.
Рішення
2 - (- 6) означає вилучити колекцію, що представляє -6 з колекції
представляючи 2. Це дає той самий результат, що і об'єднання колекції, що представляє 2, з колекцією, що представляє протилежність -6, тобто об'єднати колекцію, що представляє 2, з колекцією, що представляє 6 (що означає об'єднати 2G з 6G). Отже, 2 - (- 6) = 2 + 6.
Поясніть, що означає кожна проблема, а потім викладіть інший спосіб отримати той самий результат
| б. 4 — 8 |
Перепишіть кожне віднімання як еквівалентну задачу додавання.
| а. 4 — 5 = _____________ |
Перепишіть кожну проблему так, щоб вона була тільки в плані додавання. Іншими словами, змініть лише кожну частину віднімання на еквівалентну частину додавання. Не обчислюйте відповідь.
Заповніть пробіли:
- Віднімання 6 - це те саме, що і додавання _____.
- Віднімання -8 - це те саме, що і додавання _____.
- Віднімання додатного числа - це те саме, що додавання ______________ числа, де це _____________ число протилежне початковому додатному числу.
- Віднімання від'ємного числа - це те саме, що додавання ______________ числа, де це _____________ число протилежне вихідному від'ємному числу.
- Віднімання числа - це те саме, що і додавання _______________ цього числа.
Єдине, на що ви повинні звернути пильну увагу, - це різниця між знаком віднімання та числом, яке віднімається. Коли ви переписуєте проблему віднімання як еквівалентну проблему додавання, ви повинні пам'ятати, щоб змінити число, яке було
віднімається до його протилежності. Це, звичайно, неправда, що 6 - 3 це те ж саме, що 6 + 3. Але правда, що 6 мінус (позитивний 3) дорівнює 6 плюс (від'ємний 3); або 6 - 3 = 6 + (- 3).
Не потрібно змінювати задачі віднімання на еквівалентні завдання додавання. Це, однак, іноді дуже корисно, оскільки проблема додавання може бути простішою для роботи. І якщо все віднімання можна записати як додавання, то потрібно лише вивчити правила додавання і застосувати їх до всіх завдань додавання або віднімання. Дозвольте мені сказати, що хоча це гарна ідея знати правила додавання і віднімання, ще важливіше мати можливість повернутися до основних понять і мати можливість використовувати маніпулятиви, щоб зрозуміти, що насправді означає додавання і віднімання.
Якщо ви заповнили правильну відповідь на 28е, то у вас є. Взаємозв'язок між додаванням і відніманням полягає в цьому факті.
Кожну задачу віднімання можна переписати як еквівалентну проблему додавання. Замість того, щоб віднімати число, ви можете додати протилежне цьому числу.
Визначення: Нехай m і n - будь-яке ціле число. Потім, m — n = m + (- n). Це називається Додавання протилежного. Пам'ятайте: -n не обов'язково негативний! Якщо n позитивний, -n від'ємний, але якщо n виявляється негативним (n - це просто змінна), то -n буде позитивним.
Повернемося до числового рядка і використаємо вектори у поєднанні з відсутнім підходом додавання для обчислення задачі віднімання. Зауважте, що це зовсім інший підхід від того, як ми це робили на початку набору вправ, коли ми робили це з виконанням і скасуванням дій. Для початку давайте розглянемо визначення віднімання з використанням підходу відсутніх доповнень.
Означення: Віднімання (Missing Addend Approach) Різниця двох чисел, m і n, записаних m — n - це число c таке, що n + c = m. Іншими словами, якщо до відніманого додається c, n, то сума - минуенд, m. Відповідь, c, називається відсутнім додатком.
Розглянемо завдання 7 — 3. Відсутній підхід доповнення стверджує, що відповіддю на цю проблему віднімання буде число, яке при додаванні до числа, показаного після знака віднімання, дорівнює числу, що передує знаку віднімання. Оскільки 3 - це число після знака віднімання, ми повинні знайти число, яке потрібно додати до 3, яке дасть відповідь 7. Використовуючи числову лінію, це означає, що якщо ви розміщуєте початкову точку вектора на 3, який вектор повинен бути намальований (відсутнє додаток все ще може розглядатися як яка дія повинна відбутися), щоб кінцева точка приземлилася на 7? Намалюйте вектор з початковою точкою на 3, а кінцевою точкою - 7. Переконайтеся, що стрілка на кінці вектора вказує на 7.
Число, яке представляє вектор, є відповіддю на задачу. Ми намагаємося знайти той відсутній додаток, який є вектором, який ми малюємо. Ілюстрація для 7 — 3 показана нижче. Вектор має довжину 4 і вказує праворуч, тому відповідь 4, який я написав над вектором (позначений і позначений відсутнім додатком), щоб вказати відповідь на проблему.

Знову ж таки, зверніть увагу, що це зовсім інший підхід до віднімання. Це зовсім не схоже на те, як ми це робили на початку набору вправ, коли ми робили це, зробивши одну дію, а потім скасувавши іншу, а потім побачивши, що одна дія могла б досягти того ж результату.
Використовуючи підхід відсутніх доповнень, показано лише один вектор, а число, яке представляє вектор, є відповіддю на задачу. Іншими словами, вектор представляє відсутні додатки, які ви шукаєте, що є різницею двох чисел. Відповідь на задачу віднімання можна знайти, намалювавши вектор, поставивши початкову точку вектора на відніманні (число, показане відразу після знака віднімання), і поставивши кінцеву точку на мінуенді (число, що передує знаку віднімання). Зверніть увагу, що це визначення має сенс лише при відніманні двох чисел, на відміну від додавання та/або віднімання декількох чисел.
Процедура віднімання двох цілих чисел за допомогою векторів та підхід відсутніх доповнень: Щоб знайти різницю m та n, намалюйте вектор з початковою точкою на n та кінцевою точкою на m. Намальований вектор є відсутнім додатком і є відповіддю на задачу: m — n.
Важливо розрізняти знак віднімання і віднімання (число, показане після знака віднімання). Також важливо не забути поставити початкову точку вектора, яка буде представляти відсутні додатки на відніманні (число ПІСЛЯ знака віднімання, і кінцева точка на minuend (число, показане перед знаком віднімання). Один метод, який я іноді використовую, - це обвести мінуенд і віднімання, а потім намалювати стрілку від відніманого до мінуенду, тому я пам'ятаю, щоб намалювати вектор з його початковою точкою на відніманому та кінцевою точкою на мінуенді.
Спробуємо проблему 2 — 9. Потім 9 + ____ = 2. Обведіть мінуенд і відніміть і намалюйте стрілку від відніманого до мінуенду перед тим, як намалювати вектор.
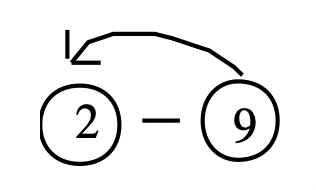
На числовій лінії намалюйте вектор з початковою точкою на 9, а кінцевою точкою - 2. Намальований спрямований вектор представляє відповідь: -7.
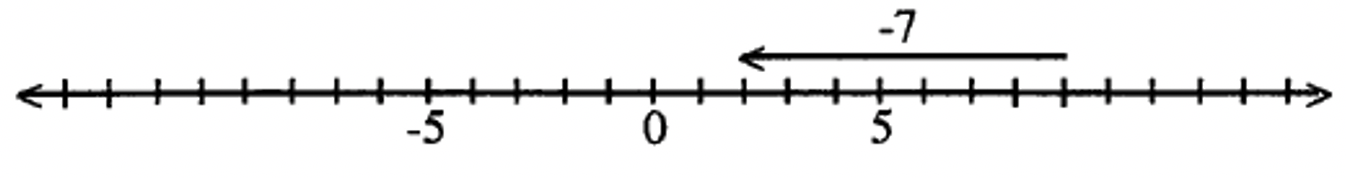
12 - (- 8). Потім -8 + ____ = 12.
Обведіть мінуенд і відніміть і намалюйте стрілку від відніманого до мінуенду перед тим, як намалювати вектор.
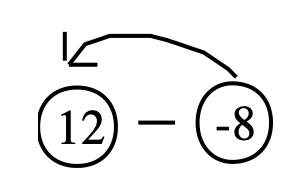
Зверніть увагу, що коли ви малюєте стрілку від віднімання до мінуенду, стрілка вказує ліворуч у фактичній задачі віднімання. Але це не має нічого спільного з тим, чи буде стрілка на векторі, який ви малюєте на цифровій лінії, буде вказувати вліво або вправо. Він вказує на мінуенд. Для цього прикладу зверніть увагу, що на відсутньому векторі доповнення, намальованому нижче, він вказує праворуч, і що відповідь на цю задачу є позитивним числом.
Помістіть початкову точку вектора на -8, а кінцеву точку на 12. Вектор, намальований нижче, показує відповідь: 20.
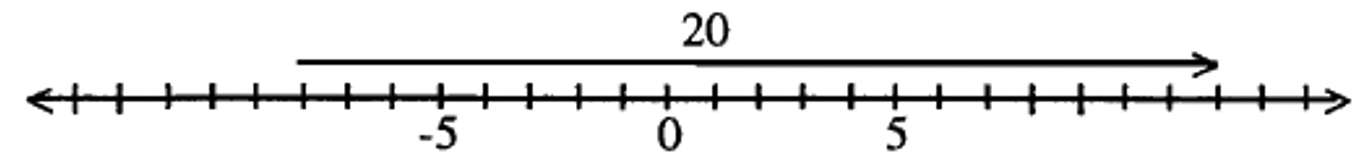
Перш ніж продовжувати, подумайте про можливість використання підходу відсутніх доповнень і навіть не отримання вектора.
- Іншими словами, що робити, якщо початкова і кінцева точка вектора знаходилася на одному і тому ж числі? Це виглядало б як точка, а не вектор. Коли це станеться?
- Якою була б відповідь на проблему, де це сталося?
Знайти відповідь на наступні задачі віднімання можна за допомогою векторів на числовому рядку у поєднанні з підходом відсутніх доповнень. Намалюйте стрілку від відніманого до мінуенду, як показано в останніх двох прикладах. Перш ніж намалювати відсутні додатки, що представляють відповідь на задачу, позначте та позначте свою цифрову лінію щонайменше 0 та однією точкою з кожного боку від нуля. Потім намалюйте вектор, який представляє відповідь на кожну задачу, і позначте вектор цим числом.
|
а. 10 — 4 = ______ 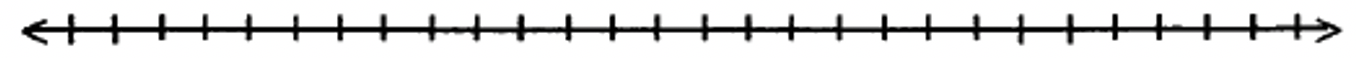 |
|
б. -7 — 5 = ______ 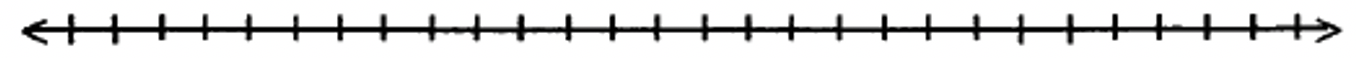 |
|
с. 8 - (- 3) = ______ 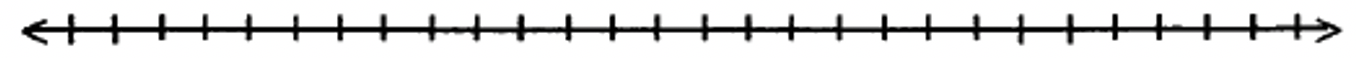 |
|
д. -9 — (- 1) = ______ 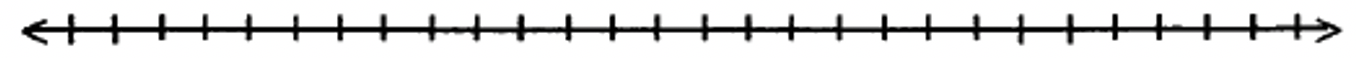 |
|
е. 3 — 10 = ______ 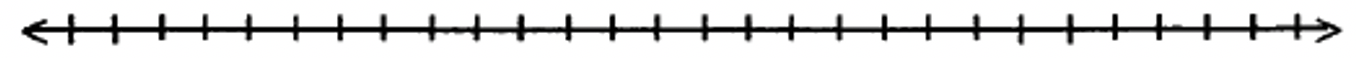 |
|
ф. -5 — (- 8) = ______ 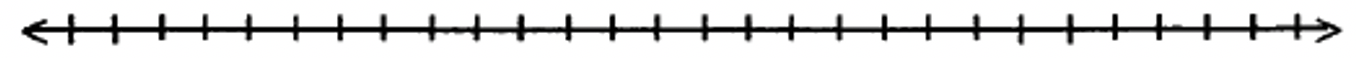 |
|
г. 6 - (- 6) = ______  |
|
ч. 9 — 9 = ______  |
Подивившись на вектори a - c нижче, з'ясуйте, яка задача віднімання виконувалася, а потім викладіть відповідь. Наприклад, вектор d прийшов від виконання завдання -1 — 5, оскільки початкова точка цього вектора знаходиться на 5, а кінцева точка - на -1. Оскільки вектор d має довжину 6 одиниць і йде вліво, він являє собою число -6. Отже, вектор d буде дорівнює: -1 — 5 = -6.
| a Вектор a: | b Вектор b: | c Вектор c: |

Одна річ, яку я люблю використовувати відсутню модель додавання, щоб показати віднімання, полягає в тому, що вона працює однаково добре при відніманні з більшими цілими числами. Просто приблизні, де цілі числа знаходяться на числовому рядку по відношенню до себе і нулю. Відповідь має сенс за допомогою моделі.
Наступні приклади показують, як використовувати вектори на числовому рядку у поєднанні з підходом відсутніх доповнень для пошуку цих відмінностей: 58 — 87, -130 — 55 та -130 — -55.
58 — 87.
Рішення
Намалюйте вектор від 87 до 58. Оскільки вектор вказує вліво, відповідь негативна, а довжина вектора становить 29 одиниць довжини, 87 — 58. Отже, 58 - 87 = -29.

-130 — 55.
Рішення
Намалюйте вектор від 55 до -130. Оскільки вектор вказує вліво, відповідь негативна, а довжина вектора становить 185 одиниць довжини, так як вона становить 130 одиниць від -130 до 0 плюс ще 55 одиниць від 0 до 55. Отже, -130 - 55 = -185.
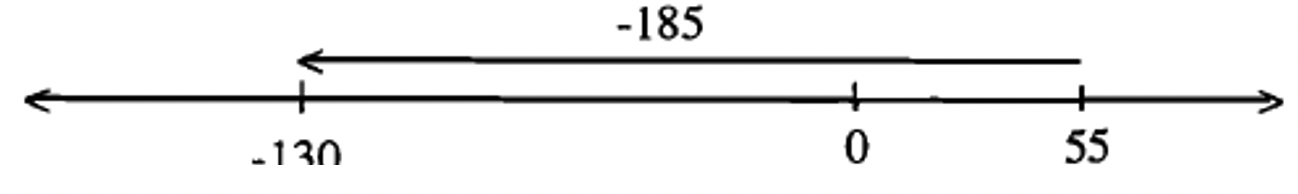
-55 - (-130).
Намалюйте вектор від -130 до -55. Оскільки вектор вказує вправо, відповідь позитивна, а довжина вектора становить 130 — 55, або 75 одиниць довжини. Отже, -55 - (-130) = 75.

Позначте та позначте числовий рядок щонайменше нулем, мінуендом (числом перед знаком віднімання) та відніманням (число, яке віднімається). Потім скористайтеся вектором, щоб знайти відповідь на проблему. Позначте вектор, який є відповіддю
|
а. -92 — (-71) = _______  |
|
б. 92 - (- 81) = _______  |
|
в. -110 - (- 200) = _______  |
|
д. -122 — 76 = _______  |
|
е. 208 — 389 = _______  |
Нарешті, ось набір правил, які завжди можна використовувати для додавання та віднімання цілих чисел без використання маніпуляцій. Поки ці правила будуть працювати завжди, краще спочатку зрозуміти, звідки взялися ці правила і чому вони працюють. Виконуючи вправи в цьому наборі вправ, тепер ви повинні мати краще розуміння того, що означає складати і віднімати з позитивними і негативними числами.
- Будь-яку задачу віднімання можна переписати як еквівалентну задачу додавання, використовуючи визначення додавання протилежного. Після того, як всі проблеми віднімання переписуються як еквівалентні проблеми додавання, залишається лише додавання, і тому нам потрібні лише правила для додавання, які слідують.
- Щоб додати числа, які мають подібні знаки (всі позитивні або всі негативні), додайте абсолютні значення чисел. Знаком відповіді буде знак вихідних чисел.
- Щоб скласти два числа з несхожими знаками (один позитивний і один негативний), візьміть різницю абсолютних значень двох чисел. Знак відповіді буде таким же, як і знак числа з більшим абсолютним значенням. Якщо абсолютні значення чисел збігаються, відповідь дорівнює нулю.
Мені ніколи не подобалося, як формулювалися ці визначення, але це математичний спосіб висловити, як саме отримати відповідь. Ось як я думаю про правила.
По-перше, я зазвичай переписую кожне віднімання як еквівалентну проблему додавання, якщо тільки це не віднімається два цілих числа. У такому випадку, якщо перше ціле число більше другого цілого числа, я роблю регулярне віднімання цілого числа. Якщо велике ціле число віднімається з меншого цілого числа, я знаю, що відповідь негативна і просто ставлю негативне число перед відповіддю.
Ось як я думаю про додавання чисел, які мають подібні знаки:
- Скажімо, ви додавали 8 + 9. Вони обидва позитивні. Таким чином, ви просто додаєте два цілих числа разом, як зазвичай, і відповідь все ще позитивна. Це все одно, що мати 8 доларів у банку, і внести ще 9 доларів. Тепер у вас в банку 17 доларів. Отже, я сподіваюся, що не дивно, що 8 + 9 = 17.
- Припустимо, ви додавали -8 + (- 9). Вони обидва негативні. Це як бути в боргах, і заглиблюватися в відділ Таким чином, ви просто додаєте два цілих числа разом, як зазвичай, але відповідь негативна. Це як завдячити комусь 8 доларів, а потім позичити ще 9 доларів. Тепер ви заборгували цій людині 17 доларів. Отже, -8 + (- 9) = - 17.
Ось як я думаю про додавання чисел, які мають несхожі знаки.
- Припустимо, ви додавали 24 + (-10). Тепер це приклад додавання двох чисел з несхожими знаками. Оскільки знаки різні, я ігнорую їх ознаки і приймаю їх РІЗНИЦЮ - це те ж саме, що просто віднімання їх абсолютних значень. Коли я ігнорую їх ознаки, я віднімаю меншу кількість від більшого числа. Потім, щоб визначити, позитивний чи негативний знак відповіді, я бачу, який з них переважує інший (чи є більше негативів чи позитивів?) — це те ж саме, що взяти знак того, що має абсолютне значення. 24 + (-10) можна вважати 24 доларами в банку і писати чек на 10 доларів. У вас все ще залишилося 14 доларів у банку. Отже, 24 + (-10) = 14.
- Якби ви додавали -24 + 10, проблема буде виконана так само, як і попередня, за винятком того, що в цьому випадку негативи переважують позитивні, тому остаточна відповідь негативна. Це як завдячити комусь 24 долари і платити їм 10 доларів. Тепер ви заборгували їм лише 14 доларів. Отже, -24 + 10 = -14.
- Скажімо, ви додавали 14 + -14 або додавали -83 + 83. В обох цих прикладах я додаю протилежності. У певному сенсі один скасовує інший. Таким чином, обидва рівні нулю. Це також можна зробити, думаючи про те, який знак переважує інший. Але жоден не переважує іншого, і це ще одна причина, що відповідь не є ні негативною, ні позитивною, а дорівнює нулю.
Використовуючи правила на початку попередньої сторінки, або те, як я думаю про це, або, можливо, якимось іншим способом ви думаєте про це, що ви впевнені, працює і має сенс, ви повинні мати можливість додавати та віднімати цілі числа з упевненістю. Ви повинні вміти пояснювати значення операцій, а також мати можливість використовувати маніпуляції та числові рядки, щоб допомогти іншим навчитися складати та віднімати з цілими числами та розуміти
Виконайте наступні арифметичні задачі, спочатку змінивши віднімання на додавання протилежного. Потім додайте два числа одночасно, працюючи зліва направо. Покажіть свої кроки.
Виконайте наступні арифметичні задачі, спочатку змінивши віднімання на додавання протилежного. Потім додайте числа з подібними знаками разом, щоб у вас була сума позитивного і негативного числа. Потім складіть ці два числа разом. Покажіть свої кроки.
Пам'ятайте, що для того, щоб набір був закритий під додавання, сума будь-яких двох елементів у наборі завжди буде в наборі. Щоб набір був закритий під віднімання, різниця будь-яких двох елементів у множині завжди буде в множині. Щоб довести, що множина не закрита під додавання або віднімання, потрібно надати контрприклад.
Для кожного з наступних наборів визначте, чи закритий набір під заданою операцією. Надайте контрприклад, якщо він не закритий
| а Цілі числа при додаванні? | б Цілі числа під відніманням? |
| c Позитивні цілі числа при додаванні? | d Позитивні цілі числа під відніманням? |
| e Від'ємні цілі числа при додаванні? | f Від'ємні цілі числа під відніманням? |
| г. {-1, 0, 1} під додаванням? | h. {-1, 0, 1} під віднімання? |
