3.3: Моделювання приросту населення

Last updated
Save as PDF

Page ID: 66598

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Як ми бачили, стохастичне моделювання значно складніше, ніж детерміноване моделювання. У міру того, як моделювання стає більш складним, числове моделювання стає необхідним. Тут, для ілюстрації, ми показуємо, як моделювати індивідуальні реалізації приросту населення.

Наївний підхід використовував би рівень народжуваності$b$ безпосередньо. Протягом короткого часового інтервалу$\Delta t$ кожна особина має$b \Delta t$ ймовірність пологів. Ми можемо вирішити, чи народжує індивід, генеруючи випадкове відхилення (псевдовипадкове число між нулем і одиницею): якщо випадкове відхилення менше$b \Delta t$, то індивід народжує; якщо більше$b \Delta t$, то індивід цього не робить. З$N$ особами в$t$ той час ми просто обчислюємо$N$ випадкові відхилення. Підрахунок кількості випадкових відхилень менше, ніж$b \Delta t$ дозволяє нам оновити чисельність населення до часу$t+\Delta t$. Для точності,$\Delta t$ повинні бути невеликими, що робить це обчислювально-повільним методом.

Існує, однак, набагато ефективніший спосіб імітації зростання населення. Визначте$\tau=\tau(N)$ випадкову величину як час, необхідний для того, щоб популяція виросла від розміру$N$ до розміру$N+1$ через одного народження. Випадкова величина$\tau$ називається інтервент-часом і являє собою минулий час між народженнями. Моделювання від розміру населення$N_{0}$ до розміру$N_{f}$ тоді просто вимагатиме обчислення$N_{f}-N_{0}$ різних випадкових значень$\tau$, відносно простого та швидкого обчислення, якщо ми знаємо функцію щільності ймовірності (pdf) $\tau$.

Відповідно, ми$P(\tau)$ визначаємо бути pdf$\tau$ для чисельності населення$N$. Функція кумулятивного розподілу (cdf)$F(\tau)$, визначена як ймовірність того, що проміжний час менше,$\tau$ що задано

\[F(\tau)=\int_{0}^{\tau} P(\tau) d \tau \nonumber \]

де$P(\tau)=F^{\prime}(\tau)$. Додаткова функція кумулятивного розподілу (ccdf)$G(\tau)$, визначена як ймовірність того, що проміжний час більше, ніж$\tau$ задано$G(\tau)=1-F(\tau)$

Тепер ймовірність того, що проміжний час більше$\tau+\Delta \tau$, ніж, при$\Delta \tau$ малому, дається ймовірністю того, що вона більше ніж в$\tau$ рази більше ймовірності того, що в часовому проміжку немає пологів$\Delta \tau$. Тому$G(\tau+\Delta \tau)$ задовольняє

\[G(\tau+\Delta \tau)=G(\tau)(1-b N \Delta \tau) \nonumber \]

Різниця$G$ та взяття межі$\Delta \tau \rightarrow 0$ дає диференціальне рівняння

\[\frac{d G}{d \tau}=-b N G \nonumber \]

які можуть бути інтегровані з використанням початкової умови$G(0)=1$ для отримання

\[G(\tau)=e^{-b N \tau} \nonumber \]

Від$G(\tau)$, ми можемо знайти

\[F(\tau)=1-e^{-b N \tau}, \quad P(\tau)=b N e^{-b N \tau} \nonumber \]

PDF$P(\tau)$, має вигляд експоненціального розподілу з параметром$b N$.

Тут ми використовуємо добре відомий результат теорії ймовірностей, який дозволяє нам обчислювати$\tau$ за допомогою випадкових відхилень. При$y$ випадковому відхиленні,$\tau$ може бути обчислена з$\tau=F^{-1}(y)$, де$F^{-1}$ знаходиться обернена функція$F .$ Правильна формула для експоненціального розподілу

\[\tau=-\frac{\ln (1-y)}{b N} \nonumber \]

Щоб імітувати чисельність населення, що зростає від$N_{0}$ до$N_{f}$, ми обчислюємо$N_{f}-N_{0}$ випадкові відхилення$y$, а потім обчислюємо відповідні проміжні часи$(3.3.6)$, використовуючи, дбаючи про коригування чисельності населення. $N$у міру зростання чисельності населення.

Нижче ми проілюструємо просту функцію MATLAB, яка імітує одну реалізацію приросту населення від початкового розміру$N_{0}$ до кінцевого розміру$N_{f}$, з народжуваністю$b$.

$clipboard_efdf560ad98aa12e8df103c9f2207bd79.png$

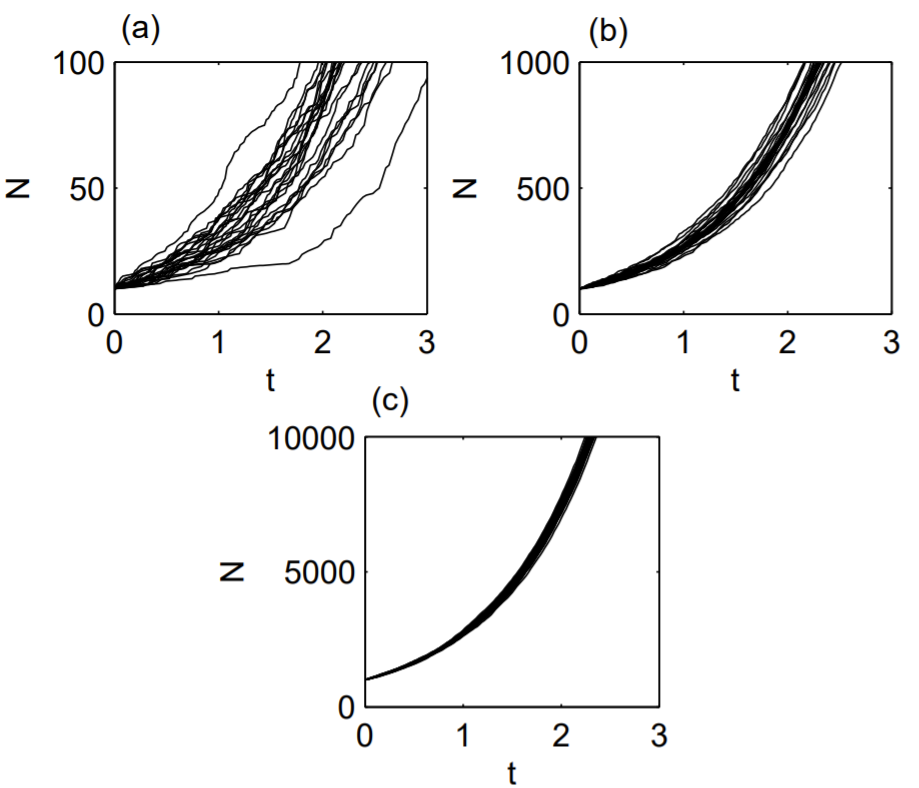
Функція population_growth_simulation.m може керуватися сценарієм MATLAB для обчислення реалізацій зростання населення. Наприклад, наступний сценарій обчислює 25 реалізацій для зростання чисельності населення від 10 до 100 з$b=1$ і графіки всіх реалізацій:

$3.1$На малюнку представлені три графіки, що показують 25 реалізацій приросту населення, починаючи з чисельності населення 10,100 і 1000, і закінчуючи чисельністю населення в 10 разів більше. Зауважте, що дисперсія відносно початкової чисельності населення зменшується зі збільшенням початкової чисельності населення, слідуючи нашому аналітичному результату (3,31). (а)

Малюнок 3.1: Двадцять п'ять реалізацій приросту населення з початковими розмірами населення 10 100 та 1000, у (a), (b) та (c) відповідно.