Skip to main content
LibreTexts - Ukrayinska

4.4: Аргументи

  1. Last updated
  2. Save as PDF
  • Page ID
    66432

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Логічним аргументом є твердження про те, що сукупність приміщень підтверджує висновок. Існує два загальних типи аргументів: індуктивні і дедуктивні аргументи.

    Типи аргументів

    Індуктивний аргумент використовує сукупність конкретних прикладів як свої передумови і використовує їх, щоб запропонувати загальний висновок.

    Дедуктивний аргумент використовує сукупність загальних тверджень як свої передумови і використовує їх, щоб запропонувати конкретну ситуацію як висновок.

    Приклад\(\PageIndex{1}\)

    Аргумент «коли я пішов в магазин минулого тижня, я забув гаманець, а коли сьогодні пішов, забув гаманець. Я завжди забуваю свій гаманець, коли йду в магазин» - це індуктивний аргумент.

    Рішення

    Приміщення:

    • Минулого тижня я забув гаманець
    • Я сьогодні забув гаманець

    Висновок такий:

    • Я завжди забуваю гаманець

    Зверніть увагу, що приміщення є конкретними ситуаціями, при цьому висновок - загальне твердження. В даному випадку це досить слабкий аргумент, так як заснований він всього на двох примірниках.

    Приклад\(\PageIndex{2}\)

    Аргумент «кожен день за минулий рік літак літає над моїм будинком о 14:00 Літак буде літати над моїм будинком щодня о 14:00» є більш сильним індуктивним аргументом, оскільки він базується на більшому наборі доказів.

    Оцінка індуктивних аргументів

    Індуктивний аргумент ніколи не може довести висновок істинний, але він може надати або слабкі, або вагомі докази, щоб припустити, що це може бути правдою.

    Багато наукових теорій, таких як теорія великого вибуху, ніколи не можуть бути доведені. Натомість вони є індуктивними аргументами, підкріпленими найрізноманітнішими доказами. Зазвичай в науці ідея вважається гіпотезою, поки вона не буде добре перевірена, і в цей момент вона закінчує вважати теорією. Загальновідомі наукові теорії, як теорія гравітації Ньютона, витримали роки випробувань та доказів, хоча іноді їх потрібно коригувати на основі нових доказів. Для гравітації це сталося, коли Ейнштейн запропонував теорію загальної відносності.

    Дедуктивний аргумент більш чітко дійсний чи ні, що полегшує їх оцінку.

    Оцінка дедуктивних аргументів

    Дедуктивний аргумент вважається дійсним, якщо всі приміщення вірні, і висновок логічно випливає з цих приміщень. Іншими словами, приміщення вірні, і висновок випливає обов'язково з тих приміщень.

    Приклад\(\PageIndex{3}\)

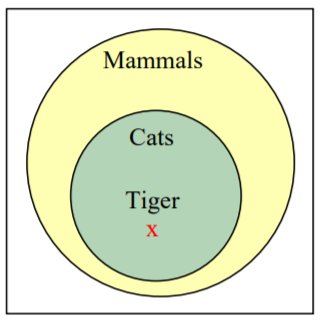
    Аргумент «Всі кішки - ссавці, а тигр - кішка, тому тигр - ссавець» є вагомим дедуктивним аргументом.

    clipboard_e022608486a9ecd90790e715961ed984b.pngПриміщення:

    • Всі кішки - ссавці
    • Тигр - кішка

    Висновок такий:

    • Тигр - ссавець

    Обидва приміщення вірні. Щоб побачити, що приміщення повинні логічно привести до висновку, одним підходом було б використання діаграми Венна. З першої передумови можна зробити висновок, що сукупність кішок є підмножиною безлічі ссавців. З другої передумови нам кажуть, що тигр лежить всередині безлічі кішок. З цього ми бачимо на діаграмі Венна, що тигр також лежить всередині безлічі ссавців, тому висновок дійсний.

    Аналіз аргументів за допомогою діаграм Венна [1]

    Аналіз аргументу за допомогою діаграми Венна

    1. Намалюйте діаграму Венна на основі передумов аргументу
    2. Якщо приміщення недостатньо для того, щоб визначити місце розташування того чи іншого елемента, вкажіть, що.
    3. Аргумент є справедливим, якщо зрозуміло, що висновок повинен бути істинним.
    Приклад\(\PageIndex{4}\)

    Передумова: Усі пожежники знають СЛР

    Передумова: Джилл знає СЛР

    Висновок: Джилл - пожежник

    Рішення

    З першої передумови ми знаємо, що всі пожежники лежать всередині безлічі тих, хто знає СЛР. З другої передумови ми знаємо, що Джилл є членом цього більшого набору, але ми не маємо достатньо інформації, щоб знати, чи є вона також членом меншої підмножини, яка є пожежниками.

    Оскільки висновок не обов'язково випливати з приміщення, це недійсний аргумент, незалежно від того, чи дійсно Джилл є пожежником.

    Важливо зазначити, що незалежно від того, чи є Джилл насправді пожежником, не важливо для оцінки обґрунтованості аргументу; ми стурбовані лише тим, чи достатньо приміщень, щоб довести висновок.

    Спробуйте зараз 2

    Визначаємо обґрунтованість цього аргументу:

    Передумова: Жодна корова не фіолетова

    Передумова: Фідо - це не корова

    Висновок: Фідо фіолетовий

    Крім цих категоричних стильових приміщень форми «всі ___», «деякі ____» та «ні ____», також часто можна побачити приміщення, які є наслідками.

    Приклад\(\PageIndex{5}\)

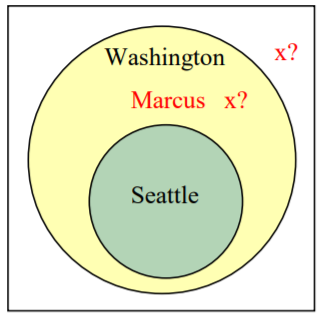    clipboard_ec90b039496bbb36e285b79d7a7845adc.pngПередумова: Якщо ви живете в Сіетлі, ви живете у Вашингтоні.

    Передумова: Маркус не живе в Сіетлі

    Висновок: Маркус не живе у Вашингтоні

    Рішення

    З першої передумови ми знаємо, що безліч людей, які живуть у Сіетлі, знаходиться всередині безлічі тих, хто живе у Вашингтоні. З другої передумови ми знаємо, що Маркус не бреше в Сіетлі, але у нас недостатньо інформації, щоб знати, чи живе Маркус у Вашингтоні чи ні. Це некоректний аргумент.

    Приклад\(\PageIndex{6}\)

    Розглянемо аргумент «Ви одружений чоловік, тому у вас повинна бути дружина».

    Рішення

    Це недійсний аргумент, оскільки є, принаймні, у частині світу, чоловіки, які одружені з іншими чоловіками, тому передумова не недостатня, щоб мати на увазі висновок.

    Деякі аргументи краще аналізувати за допомогою таблиць істинності.

    Приклад\(\PageIndex{7}\)

    Розглянемо аргумент

    Приміщення: Якщо ви купили хліб, то пішли в магазин

    Передумова: Ви купили хліб

    Висновок: Ви пішли в магазин

    Хоча цей приклад, сподіваюся, досить очевидно є вагомим аргументом, ми можемо проаналізувати його за допомогою таблиці істинності, представляючи кожне з приміщень символічно. Потім ми можемо подивитися на наслідки того, що приміщення разом мають на увазі висновок. Якщо таблиця істинності є тавтологією (завжди вірно), то аргумент є дійсним.

    Ми отримаємо\(B\) представляємо «ви купили хліб» і\(S\) представляємо «ви пішли в магазин». Тоді аргументом стає:

    Передумова:\(B → S\)

    Передумова:\(B\)

    Висновок:\(S\)

    Щоб перевірити обґрунтованість, ми дивимося, чи передбачає поєднання обох приміщень висновок; чи правда це\(\left[ (B→S) ⋀ B \right] → S\)?

    Б S Б→С (Б → С) B [(B → S) B] → S
    Т Т Т Т Т
    Т F F F Т
    F Т Т F Т
    F F Т F Т

    Оскільки таблиця істинності для\(\left[ (B→S) ⋀ B \right] → S\) завжди вірна, це вагомий аргумент.

    Спробуйте зараз 3

    Визначте, чи є аргумент дійсним:

    Приміщення: Якщо у мене є лопата, я можу викопати яму.

    Приміщення: Я викопав яму

    Висновок: Тому у мене була лопата

    Аналіз аргументів за допомогою таблиць істинності

    Щоб проаналізувати аргумент за допомогою таблиці істинності:

    1. Представляють кожне з приміщень символічно
    2. Створіть умовний оператор, з'єднавши всі приміщення з і сформувавши попередній, і використовуючи висновок як наслідок.
    3. Створіть таблицю істинності для цього твердження. Якщо він завжди істинний, то аргумент є дійсним.
    Приклад\(\PageIndex{8}\)

    Передумова: Якщо я піду в торговий центр, то куплю нові джинси

    Передумова: Якщо я куплю нові джинси, я куплю сорочку, щоб піти з нею

    Висновок: Якщо я потрапив до торгового центру, куплю сорочку.

    Рішення

    Нехай\(M\) = я йду в торговий центр,\(J\) = купую джинси, а\(S\) = купую сорочку.

    Приміщення і висновок можуть бути викладені як:

    Приміщення: M → J

    Передумова: J → S

    Висновок: M → S

    Ми можемо побудувати таблицю істинності для\([(M→J) ⋀ (J→S)] → (M→S)\)

    М J S М→Дж J→S (М → ДЖ) (ДЖ→С) М→С [(М → ДЖ) (ДЖ→С)] → (М → С)
    Т Т Т Т Т Т Т Т
    Т Т F Т F F F Т
    Т F Т F Т F Т Т
    Т F F F Т F F Т
    F Т Т Т Т Т Т Т
    F Т F Т F F Т Т
    F F Т Т Т Т Т Т
    F F F Т Т Т Т Т

    З таблиці істинності ми бачимо, що це вагомий аргумент.

    Попередня проблема - приклад силогізму.

    Визначення: Силогізм

    Силогізм - це підтекст, похідний від двох інших, де наслідком одного є попередник іншого. Загальна форма силогізму - це:

    Передумова: p → q

    Передумова: q → r

    Висновок: р → р

    Це іноді називають перехідним властивістю для імплікації.

    Приклад\(\PageIndex{9}\)

    Передумова: Якщо я наполегливо працюю, я отримаю підвищення.

    Передумова: Якщо я отримаю підвищення, я куплю човен.

    Висновок: Якщо я не купую човен, я, мабуть, не працював.

    Рішення

    Якщо ми дозволимо W = наполегливо працювати, R = отримати підвищення, а B = покупка човна, то ми можемо символічно представити наш аргумент:

    Передумова: H → R

    Передумова: R → B

    Висновок: ~ B → ~ H

    Ми могли б побудувати таблицю істинності для цього аргументу, але замість цього ми будемо використовувати позначення контрапозитивного, який ми дізналися раніше, щоб відзначити, що імплікація ~ B → ~ H еквівалентна імплікації H → B. Переписаний, ми бачимо, що цей висновок дійсно є логічним силогізмом, похідним з передумов.

    Спробуйте зараз 4

    Чи є цей аргумент справедливим?

    Передумова: Якщо я піду на вечірку, завтра я буду дуже втомлений.

    Передумова: Якщо я піду на вечірку, я побачу друзів.

    Висновок: Якщо я не побачу друзів, завтра не втомлюся.

    Льюїс Керролл, автор книги «Аліса в країні чудес», був учителем математики та логіки, і написав дві книги з логіки. У них він пропонував би приміщення як головоломку, пов'язану за допомогою силогізмів.

    Приклад\(\PageIndex{10}\)

    Вирішити головоломку. Іншими словами, знайдіть логічний висновок з цих приміщень.

    • Всі малюки нелогічні.
    • Ніхто не зневажає, хто може управляти крокодилом.
    • Нелогічних осіб зневажають
    Рішення

    Нехай B = це немовля, D = зневажається, I = нелогічно, а М = може управляти крокодилом.

    Тоді ми можемо записати приміщення як:

    Б → I

    М → ~Д

    I → Д

    З першого і третього передумов можна зробити висновок, що B → D; що немовлят зневажають. Використовуючи контрапозитив другого приміщення, D → ~M, можна зробити висновок, що B → ~M; що немовлята не можуть керувати крокодилами.

    Поки нерозумно, це логічний висновок з даного приміщення.