17.11: Форми вагомих аргументів
- Page ID
- 66448
Замість того, щоб складати таблицю істини для кожного аргументу, ми можемо розпізнати певні поширені форми аргументів, які є дійсними (або недійсними). Якщо ми можемо визначити, що аргумент відповідає одній із загальних форм, ми можемо одразу заявити, чи є він дійсним чи недійсним.
Закон відсторонення застосовується, коли умовний і його попередник даються як приміщення, а наслідком є висновок. Загальна форма така:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & p \\ \text{Conclusion:} & q \end{array}\)
Латинська назва, modus ponens, перекладається як «режим, який підтверджує».
Згадаймо цей аргумент з більш раннього прикладу:
\(\begin{array} {ll} \text{Premise:} & \text{If you bought bread, then you went to the store.} \\ \text{Premise:} & \text{You bought bread.} \\ \text{Conclusion:} & \text{You went to the store.} \end{array}\)
В символічній формі:
\(\begin{array} {ll} \text{Premise:} & b \rightarrow s \\ \text{Premise:} & b \\ \text{Conclusion:} & s \end{array}\)
Цей аргумент має структуру, описану законом відстороненості. (Друга передумова і висновок - це просто дві частини першого приміщення, відокремлені один від одного.) Замість того, щоб скласти таблицю правди, можна сказати, що цей аргумент є справедливим, заявивши, що він задовольняє закону відстороненості.
Закон контрапозиції застосовується, коли умовне і заперечення його наслідку даються як передумови, а заперечення його попередником є висновок. Загальна форма така:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & \sim q \\ \text{Conclusion:} & \sim p \end{array}\)
Латинська назва, modus tollens, перекладається як «режим, який заперечує».
Зверніть увагу, що друга передумова та висновок виглядають як контрапозитив першої передумови\(\sim q \rightarrow \sim p\), але вони були відокремлені. Можна думати про закон контрапозиції як про поєднання закону відстороненості і того факту, що контрапозитив логічно еквівалентний вихідному твердженню.
\(\begin{array} {ll} \text{Premise:} & \text{If I drop my phone into the swimming pool, my phone will be ruined.} \\ \text{Premise:} & \text{My phone isn’t ruined.} \\ \text{Conclusion:} & \text{I didn’t drop my phone into the swimming pool.} \end{array}\)
Якщо ми\(d=\mathrm{I}\) дозволимо кинути телефон в\(r=\) пулі і телефон зруйнований, то ми можемо представити аргумент таким чином:
\(\begin{array} {ll} \text{Premise:} & d \rightarrow r \\ \text{Premise:} & \sim r \\ \text{Conclusion:} & \sim d \end{array}\)
Форма цього аргументу відповідає тому, що нам потрібно викликати закон контрапозиції, тому він є дійсним аргументом.
Чи є цей аргумент справедливим?
\(\begin{array} {ll} \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\ \text{Premise:} & \text{Your toothbrush is dry.} \\ \text{Conclusion:} & \text{You didn’t brush your teeth before bed.} \end{array}\)
- Відповідь
-
Нехай\(b=\) чищені зуби і\(w=\) зубна щітка мокрі.
\(\begin{array} {ll} \text{Premise:} & b \rightarrow w \\ \text{Premise:} & \sim w \\ \text{Conclusion:} & \sim b \end{array}\)
Цей аргумент є справедливим за Законом протиставлення.
Перехідна властивість має в якості своїх приміщень низку умовних, де наслідком одного є попередник наступного. Висновок є умовним з тим самим попередником, що і перша передумова, і тим самим наслідком, що і остаточна передумова. Загальна форма така:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & q \rightarrow r \\ \text{Conclusion:} & p \rightarrow r \end{array}\)
Більш ранній приклад покупки сорочки в торговому центрі є прикладом, що ілюструє перехідну властивість. У ній описується ланцюгова реакція: якщо відбувається перше, то відбувається друге, а якщо відбувається друге, то відбувається третє. Тому, якщо ми хочемо ігнорувати друге, ми можемо сказати, що якщо трапиться перше, то ми знаємо, що станеться третє. Ми не повинні згадувати частину про покупку джинсів, ми можемо просто сказати, що перша подія веде до фінальної події. Ми могли б навіть мати більше двох приміщень; поки вони утворюють ланцюгову реакцію, перехідна властивість дасть нам вагомий аргумент.
\(\begin{array} {ll} \text{Premise:} & \text{If a soccer player commits a reckless foul, she will receive a yellow card.} \\ \text{Premise:} & \text{If Hayley receives a yellow card, she will be suspended for the next match.} \\ \text{Conclusion:} & \text{If Hayley commits a reckless foul, she will be suspended for the next match.} \end{array}\)
Якщо ми\(r=\) дозволимо вчинити безрозсудний фол,\(y=\) отримати жовту картку, і\(s=\) бути призупиненим, то наш аргумент виглядає так:
\(\begin{array} {ll} \text{Premise:} & r \rightarrow y \\ \text{Premise:} & y \rightarrow s \\ \text{Conclusion:} & r \rightarrow s \end{array}\)
Цей аргумент має точну структуру, необхідну для використання перехідної властивості, тому він є дійсним аргументом.
Чи є цей аргумент справедливим?
\(\begin{array} {ll} \text{Premise:} & \text{If the old lady swallows a fly, she will swallow a spider.} \\ \text{Premise:} & \text{If the old lady swallows a spider, she will swallow a bird.} \\ \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\ \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\\text{Premise:} & \text{If the old lady swallows a bird, she will swallow a cat.} \\ \text{Premise:} & \text{If the old lady swallows a cat, she will swallow a dog.} \\\text{Premise:} & \text{If the old lady swallows a dog, she will swallow a goat.} \\ \text{Premise:} & \text{If the old lady swallows a goat, she will swallow a cow.} \\ \text{Premise:} & \text{If the old lady swallows a cow, she will swallow a horse.} \\ \text{Premise:} & \text{If the old lady swallows a horse, she will die, of course.} \\ \text{Conclusion:} & \text{If the old lady swallows a fly, she will die, of course.} \end{array}\)
- Відповідь
-
Цей аргумент справедливий перехідною властивістю, яка може включати більше двох приміщень, доки вони продовжують ланцюгову реакцію. Приміщення\(f \rightarrow s, s \rightarrow b, b \rightarrow c, c \rightarrow d\)\(d \rightarrow g, g \rightarrow w, w \rightarrow h, h \rightarrow x\) можна скоротити до\(f \rightarrow x. \) (Тому що ми вже використовували\(c\) і\(d\) ми вирішили використовувати\(w\) для корови і\(x\) для смерті. Якщо старенька проковтне муху, вона з часом з'їсть коня і помре.
У диз'юнктивному силогізмі приміщення складаються з заяви або та заперечення одного з варіантів. Висновок - інший варіант. Загальна форма така:
\(\begin{array} {ll} \text{Premise:} & p \vee q \\ \text{Premise:} & \sim p \\ \text{Conclusion:} & q \end{array}\)
Порядок двох частин диз'юнкції не важливий. Іншими словами, ми могли б мати приміщення\(p \vee q\)\(\sim q,\) і висновок\(p\)
\(\begin{array} {ll} \text{Premise:} & \text{I can either drive or take the train.} \\ \text{Premise:} & \text{I refuse to drive.} \\ \text{Conclusion:} & \text{I will take the train.} \end{array}\)
Якщо ми дозволимо\(d=I\) їздити і\(t=I\) взяти поїзд, то символічне зображення аргументу:
\(\begin{array} {ll} \text{Premise:} & d \vee t \\ \text{Premise:} & \sim d \\ \text{Conclusion:} & t \end{array}\)
Цей аргумент є справедливим, оскільки має форму диз'юнктивного силогізму. У мене є два варіанти, і один з них не відбудеться, тому інший повинен відбутися.
Чи є цей аргумент справедливим?
\(\begin{array} {ll} \text{Premise:} & \text{Alison was required to write a 10-page paper or give a 5-minute speech.} \\ \text{Premise:} & \text{Alison did not give a 5-minute speech.} \\ \text{Conclusion:} & \text{Alison wrote a 10-page paper.} \end{array}\)
- Відповідь
-
Нехай\(p=\) написав статтю і\(s=\) виступив з промовою.
\(\begin{array} {ll} \text{Premise:} & p \vee s \\ \text{Premise:} & -s \\ \text{Conclusion:} & p \end{array}\)
Цей аргумент справедливий диз'юнктивним силогізмом. Елісон повинна була зробити те чи інше; вона не вибрала промову, тому вона, мабуть, обрала папір.
Майте на увазі, що, коли ви визначаєте обґрунтованість аргументу, ви повинні вважати, що приміщення є істинними. Якщо ви не згодні з одним із приміщень, вам потрібно тримати свою особисту думку поза ним. Ваша робота полягає в тому, щоб зробити вигляд, що приміщення є істинними, а потім визначити, чи змушують вони вас прийняти висновок. Звичайно, ви можете напасти на приміщення в суді чи політичній дискусії, але тут ми зосереджуємось на структурі аргументів, а не на правді того, що вони насправді говорять.
Ми щойно розглянули чотири форми достовірних аргументів; є дві загальні форми, які представляють недійсні аргументи, які також називаються помилками.
Помилковість зворотного виникає, коли умовне та його наслідок даються як передумови, а попередник - висновок. Загальна форма така:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & q \\ \text{Conclusion:} & p \end{array}\)
Зверніть увагу, що друга передумова та висновок виглядають як зворотне перше приміщення\(q \rightarrow p\), але вони були відокремлені. Помилка зворотного невірно намагається стверджувати, що зворотне твердження еквівалентно цьому твердженню.
\(\begin{array} {ll} \text{Premise:} & \text{If I drink coffee after noon, then I have a hard time falling asleep that night.} \\ \text{Premise:} & \text{I had a hard time falling asleep last night.} \\ \text{Conclusion:} & \text{I drank coffee after noon yesterday.} \end{array}\)
Якщо ми даємо\(c=\mathrm{I}\) пити каву після полудня і важко\(h=\mathrm{I}\) засинаємо, то наш аргумент виглядає так:
\(\begin{array} {ll} \text{Premise:} & c \rightarrow h \\ \text{Premise:} & h \\ \text{Conclusion:} & c \end{array}\)
Цей аргумент використовує зворотні міркування, тому він є недійсним аргументом. Може бути багато інших причин, чому я не міг заснути: я міг турбуватися про гроші, мої сусіди, можливо, вирушили феєрверки,...
Чи є цей аргумент справедливим?
\(\begin{array} {ll} \text{Premise:} & \text{If you pull that fire alarm, you will get in big trouble.} \\ \text{Premise:} & \text{You got in big trouble.} \\ \text{Conclusion:} & \text{You must have pulled the fire alarm.} \end{array}\)
- Відповідь
-
Нехай\(f=\) потягнув пожежну сигналізацію і\(t=\) потрапив у велику біду.
\(\begin{array} {ll} \text{Premise:} & f \rightarrow t \\ \text{Premise:} & t \\ \text{Conclusion:} & f \end{array}\)
Помилковість зворотного виникає, коли умовне і заперечення його попередження даються як передумови, а заперечення наслідку - висновок. Загальна форма така:
\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & \sim p \\ \text{Conclusion:} & \sim q \end{array}\)
Знову ж таки, зверніть увагу, що друга передумова і висновок виглядають як зворотна перша передумова\(\sim p \rightarrow \sim q\), але вони були відокремлені. Помилка зворотного неправильно намагається стверджувати, що зворотне твердження еквівалентно цьому твердженню.
\(\begin{array} {ll} \text{Premise:} & \text{If you listen to the Grateful Dead, then you are a hippie.} \\ \text{Premise:} & \text{Sky doesn’t listen to the Grateful Dead.} \\ \text{Conclusion:} & \text{Sky is not a hippie.} \end{array}\)
Якщо ми\(g=\) дозволимо слухати вдячних мертвих і\(h=\) є хіпі, то це аргумент:
\(\begin{array} {ll} \text{Premise:} & g \rightarrow h \\ \text{Premise:} & \sim g \\ \text{Conclusion:} & \sim h \end{array}\)
Цей аргумент є недійсним, оскільки він використовує зворотні міркування. Перша передумова не означає, що всі хіпі слухають вдячних мертвих; там можуть бути хіпі, які замість цього слухають Фіша.
Чи є цей аргумент справедливим?
\(\begin{array} {ll} \text{Premise:} & \text{If a hockey player trips an opponent, he will be assessed a 2-minute penalty.} \\ \text{Premise:} & \text{Alexei did not trip an opponent.} \\ \text{Conclusion:} & \text{Alexei will not be assessed a 2-minute penalty.} \end{array}\)
- Відповідь
-
Нехай\(t=\)\(p=\) спіткнувся і отримав пенальті.
\(\begin{array} {ll} \text{Premise:} & t \rightarrow p \\ \text{Premise:} & \sim t \\ \text{Conclusion:} & \sim p \end{array}\)
Цей аргумент є недійсним, оскільки він має форму помилкового зворотного. Олексій, можливо, отримав штраф за порушення, відмінне від споткання.
Звичайно, аргументи не обмежуються цими шістьма основними формами; деякі аргументи мають більше приміщень або приміщень, які потрібно переставити, перш ніж ви зможете побачити, що насправді відбувається. Існує безліч інших форм аргументів, які є недійсними. Якщо аргумент, здається, не відповідає шаблону будь-якої з цих загальних форм, ви можете використовувати діаграму Венна або таблицю істинності.
Льюїс Керролл, автор книги «Пригоди Аліси в країні чудес», був викладачем математики та логіки, і написав дві книги з логіки. У них він пропонував би приміщення як головоломку, пов'язану за допомогою силогізмів. Наступний приклад - одна з таких головоломок.
Вирішіть головоломку. Іншими словами, знайдіть логічний висновок з цих приміщень.
Всі немовлята нелогічні.
Ніхто не зневажає, хто може управляти крокодилом.
Нелогічних осіб зневажають.
Нехай\(b=\) немовля,\(d=\)\(i=\) зневажається, нелогічний, і\(m=\) може управляти крокодил.
Тоді ми можемо записати приміщення як:
\(b \rightarrow i\)
\(m \rightarrow \sim d\)
\(i \rightarrow d\)
Правильне написання другої передумови може бути складним завданням; його можна перефразувати як «Якщо ви можете керувати крокодилом, то вас не зневажають».
Використовуючи перехідне властивість з першим і третім приміщенням, можна зробити висновок про те\(b \rightarrow d\), що всі малюки зневажають. Використовуючи контрапозитив другої передумови\(d \rightarrow \sim m\), ми можемо потім використовувати перехідну властивість з\(b \rightarrow d\) зробити висновок про те\(b \rightarrow \sim m\), що немовлята не можуть керувати крокодилами. Поки це нерозумно, це логічний висновок з даного приміщення.
\(\begin{array} {ll} \text{Premise:} & \text{If I work hard, I’ll get a raise.} \\ \text{Premise:} & \text{If I get a raise, I’ll buy a boat.} \\ \text{Conclusion:} & \text{If I don’t buy a boat, I must not have worked hard.} \end{array}\)
Якщо ми дозволимо наполегливо\(h=\) працювати,\(r=\) отримувати підвищення та\(b=\) купувати човен, то ми можемо символічно представити наш аргумент:
\(\begin{array} {ll} \text{Premise:} & h \rightarrow r \\ \text{Premise:} & r \rightarrow b \\ \text{Conclusion:} & \sim b \rightarrow \sim h \end{array}\)
Використовуючи перехідне майно з двома приміщеннями, можна зробити висновок\(h \rightarrow b\), що, якщо я багато працюю, то куплю човен. Коли ми дізналися про контрапозитив, ми побачили, що\(h \rightarrow b\) умовний оператор еквівалентний\(\sim b \rightarrow \sim h\). Тому висновок дійсно є логічним силогізмом, отриманим з приміщення.
Чи є цей аргумент справедливим?
\(\begin{array} {ll} \text{Premise:} & \text{If I go to the party, I’ll be really tired tomorrow.} \\ \text{Premise:} & \text{If I go to the party, I’ll get to see friends.} \\ \text{Conclusion:} & \text{If I don’t see friends, I won’t be tired tomorrow.} \end{array}\)
- Відповідь
-
\(p=\)Відпустіть на вечірку,\(t=\) втомлюйтеся і\(f=\) побачите друзів.
\(\begin{array} {ll} \text{Premise:} & p \rightarrow t \\ \text{Premise:} & p \rightarrow f \\ \text{Conclusion:} & -f \rightarrow \sim t \end{array}\)
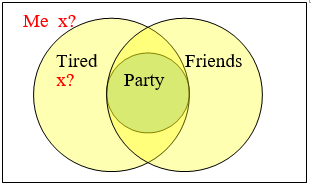Ми могли б спробувати переписати другу передумову, використовуючи контрапозитивний стан\(\sim f \rightarrow \sim p\), але це не дозволяє нам сформувати силогізм. Якщо я не бачу друзів, то я не пішов на вечірку, але цього недостатньо, щоб стверджувати, що завтра не втомлюся. Можливо, я не спав всю ніч, переглядаючи фільми.Діаграма Венна може допомогти, якщо ми правильно її налаштуємо. «Партійний» коло повинен повністю міститися в межах перетину інших кіл. Ми знаємо, що я десь поза колом «друзів», але не можемо визначити, чи перебуваю я в «втомленому» колі. Все, що ми дійсно знаємо точно, це те, що я не пішов на вечірку.