16.5: Криптографія з відкритим ключем
- Page ID
- 66158
Припустимо, що ви підключаєтеся до веб-сайту свого банку. Цілком можливо, що хтось може перехопити будь-яке спілкування між вами і вашим банком, тому ви захочете зашифрувати зв'язок. Проблема полягає в тому, що всі методи шифрування, які ми обговорювали, вимагають, ніж обидві сторони вже домовилися про спільний секретний ключ шифрування. Як ви і ваш банк можете домовитися про ключ, якщо ви ще цього не зробили?
Це стає метою криптографії з відкритим ключем - надати можливість двом сторонам домовитися про ключ без того, щоб третя сторона могла визначити ключ. Метод спирається на односторонню функцію; те, що легко зробити в одну сторону, але важко змінити. Ми вивчимо метод обміну ключами Діффі-Хеллмана-Меркла.
Як приклад розглянемо змішування фарби. Легко змішати фарбу, щоб отримати новий колір, але набагато складніше розділити змішану фарбу на два використані оригінальні кольори [1] [2]
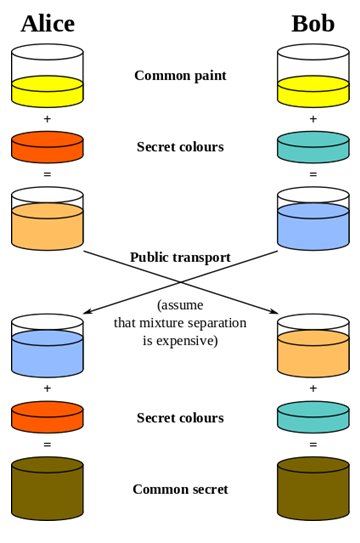Використовуючи цю аналогію, Аліса і Боб публічно погоджуються на загальному стартовому кольорі. Потім кожен змішується в деяких з власного секретного кольору. Потім вони обмінюються своїми змішаними кольорами.
Оскільки розділити кольори важко, навіть якби снупер отримував ці змішані кольори, було б важко отримати оригінальні секретні кольори.
Після того, як вони обмінялися своїми змішаними кольорами, Аліса та Боб обидва додають свій секретний колір до суміші, яку вони отримали від іншої людини. При цьому і Аліса, і Боб тепер мають однаковий загальний таємний колір, оскільки він містить суміш оригінального загального кольору, таємного кольору Аліси та секретного кольору Боба.
Тепер вони мають загальний секретний колір, який вони можуть використовувати як ключ шифрування, хоча ні Аліса, ні Боб не знають секретного кольору іншого.
Так само для снупера немає можливості отримати загальний секретний колір, не відокремлюючи один із змішаних кольорів.
Щоб змусити цей процес працювати для комп'ютерного спілкування, нам потрібно мати результат процесу в спільному номері, щоб діяти як загальний секретний ключ шифрування. Для цього нам знадобиться числова одностороння функція.
Модульна арифметика
Якщо ви згадаєте про поділ цілими числами, ви можете пам'ятати, що знайти результат цілого числа та залишок після ділення.
Модуль пружності [3]
Модуль - це інша назва залишку після ділення.
Наприклад, 17 мод 5 = 2, так як якщо розділити 17 на 5, то отримаємо 3 з залишком 2.
Модульну арифметику іноді називають арифметикою годинника, оскільки аналогові годинники обертаються навколо разів за 12, тобто вони працюють на модулі 12. Якщо годинна стрілка годинника в даний час вказує на 8, то через 5 годин вона буде вказувати на 1. У\(8+5 = 13\) той час як годинник обертається навколо після 12, тому всі часи можна розглядати як модуль 12. Математично 13 мод 12 = 1.
Обчислити: а) 10 мод 3 б) 15 мод 5 с)\(2^{7}\) мод 5
Рішення
а) Оскільки 10 ділиться на 3 є 3 з залишком 1,10 мод\(3=1\)
б) Оскільки 15 ділиться на 5 є 3 без залишку, 15 мод\(5=0\)
в)\(2^{7}=128.128\) ділити на 5 дорівнює 25 з залишком\(3,\) так\(2^{7}\) мод\(5=3\)
Обчислювач: а) 23 мод 7 б) 15 мод 7 c) 2034 мод 7
- Відповідь
-
а) 2 б) 1 в) 4
Нагадаємо, що коли ми ділимо 17 на 5, ми могли б представити результат як 3 залишок 2, як змішане число\(3\frac{2}{5}\), або як десяткове 3.4. Зверніть увагу, що модуль, 2, такий же, як чисельник дробової частини змішаного числа, і що десяткова частина 0,4 еквівалентна дробу. Ми можемо використовувати ці перетворення для обчислення модуля не надто величезних чисел на стандартному калькуляторі.
Розрахувати\(a\) мод\(n\) на стандартному калькуляторі
- Розділити\(a\) на\(n\)
- Відніміть всю частину отриманої кількості
- Помножте\(n\) на, щоб отримати модуль
Розрахувати 31345 мод 419
Рішення
\(\begin{array}{ll} 31345 / 419=74.8090692 & \text{Now subtract 74 to get just the decimal remainder} \\ 74.8090692-74=0.8090692 & \text{Multiply this by 419 to get the modulus} \\ 0.8090692 \times 419=339 & \text{This tells us 0.8090692 was equivalent to }\frac{339}{419} \end{array}\)
У тексті вище була записана лише частина десяткового значення. На практиці слід намагатися уникати записування кроків посередника, а замість цього дозволити калькулятору зберігати якомога більше десяткових значень.
Функція одностороннього руху
Коли ви використовуєте просте число\(p\) як модуль, ви можете знайти спеціальне число, яке називається генератором,\(g,\) так що\(g^{n}\) мод\(p\) призведе до всіх значень від 1 до\(p-1\)
\ (\ почати {масив} {|l|l|l|}
\ hline n & 3^ {n} & 3^ {n}\ mathrm {мод} 7
\\\ лінія 1 & 3\
\\ рядок 2 & 9 & 2\\
\ лінія 3 & 27\\\
\ hline 4 & 81 & 4\\
\ hline 5 & 243 & 5\\
\ hline 6 & 729 & 1\\
\ hline
\ кінець {масив}\)
У таблиці вгорі зверніть увагу, що коли ми даємо значення\(n\) від 1 до\(6,\) ми отримуємо всі значення від 1 до\(6 .\) Це означає 3 є генератором, коли 7 модуль.
Це дає нам нашу односторонню функцію. Хоча легко обчислити значення\(g^{n}\) мода\(n\),\(p\) коли ми знаємо, важко знайти показник\(n\) для отримання конкретного значення.
Наприклад, припустимо, що ми використовуємо\(p=23\) і\(g=5 .\) якщо я\(n\) вибираю бути,\(6,\) я можу досить легко обчислити\(5^{6}\) мод\(23=15625\) мод\(23=8\)
Якщо хтось інший повинен був вам сказати\(5^{n} \bmod 23=7\), це набагато складніше знайти\(n\). У цьому конкретному випадку нам доведеться спробувати 22 різних значень,\(n\) поки ми не знайшли той, який працював - немає ніякого відомого простішого способу знайти\(n\) інший, ніж ворожіння з грубою силою.
При спробі 22 значення не займе занадто багато часу, коли використовуються на практиці набагато більші значення для\(p\) використовуються, як правило, з більш ніж 500 цифр. Спробувати всі можливості було б по суті неможливо.
Обмін ключами
Перш ніж ми зможемо розпочати процес обміну ключами, нам знадобиться ще пара важливих фактів про модульну арифметику.
\(\left(a^{b} \bmod n\right)=(a \bmod n)^{b} \bmod n\)
Обчислити\(12^{5}\) мод 7 за допомогою правила піднесення до степеня.
Рішення
Оцінюється безпосередньо:\(12^{5}=248,832,\) так\(12^{5}\) мод\(7=248,823\) мод\(7=3\)
Використовуючи наведене вище правило,\(12^{5}\) мод\(7=(12 \bmod 7)^{5} \bmod 7=5^{5} \bmod 7=3125 \bmod 7=3\)
Ви можете запам'ятати основне правило показника з алгебри:
\[\left(a^{b}\right)^{c}=a^{b c}=a^{c b}=\left(a^{c}\right)^{b} \nonumber \]
Наприклад:
\[64^{2}=\left(4^{3}\right)^{2}=4^{6}=\left(4^{2}\right)^{3}=16^{3} \nonumber \]
Ми можемо об'єднати модульне правило експоненції з правилом алгебри експоненти, щоб визначити модульне правило потужності експоненти.
\[\left(a^{b} \bmod n\right)^{c} \bmod n=\left(a^{b c} \bmod n\right)=\left(a^{c} \bmod n\right)^{b} \bmod n \nonumber \]
Перевірте наведене вище правило, якщо\(a=3, b=4, c=5,\) і\(n=7\)
Рішення
\(\left(3^{4} \bmod 7\right)^{5} \bmod 7=(81 \bmod 7)^{5} \bmod 7=4^{5} \bmod 7=1024 \bmod 7=2\)
\(\left(3^{5} \bmod 7\right)^{4} \bmod 7=(243 \bmod 7)^{4} \bmod 7=5^{4} \bmod 7=625 \bmod 7=2,\)той же результат.
Використовуйте правило модульної експоненти для обчислення,\(10000 \bmod 7,\) відзначивши\(10000=10^{4}\)
- Відповідь
-
\(10000 \bmod 7=10^{4} \bmod 7=(10 \bmod 7)^{4} \bmod 7=3^{4} \bmod 7=81 \bmod 7=4\)
Це дає нам основу для нашого обміну ключами. Хоча це буде легше зрозуміти в наступному прикладі, ось процес:
- Аліса і Боб публічно погоджуються на цінності простого\(p\) і генератора\(g\).
- Аліса вибирає якийсь секретний номер, в\(a,\) той час як Боб вибирає якийсь секретний номер\(b\).
- Аліса обчислює\(A=g^{2} \bmod p\) і відправляє його Бобу.
- Боб обчислює\(B=g^{b}\) мод\(p\) і відправляє його Алісі.
- Аліса обчислює\(B^{a} \bmod p,\), який є\(\left(g^{b} \bmod p\right)^{a} \bmod p\).
- Боб обчислює\(A^{b} \bmod p,\), що є\(\left(g^{a} \bmod p\right)^{b} \bmod p\).
Модульне правило потужності експоненти говорить нам,\(\left(g^{a} \bmod p\right)^{b} \bmod p=\left(g^{b} \bmod p\right)^{a} \bmod p,\) що Аліса і Боб отримають однакове спільне значення для використання в якості ключа, хоча жоден не знає секретного номера іншого, і жоден підслуховувач не може визначити це значення, знаючи лише\(g, p, A,\) і\(B\)
Аліса і Боб публічно поділяють генератор і простий модуль. У цьому випадку ми будемо використовувати 3 як генератор і 17 як простий.
Рішення
\(\begin{array}{llll} & \textbf{Alice} & & \textbf{Bob} \\ \text{Alice and Bob publically} & g=3, p=17 & \text{Common info} & g=3, p=17 \\ \text{share a generator and prime} & & & \\ \text{modulus.} & & & \\ \text{Each then secretly picks a} & n = 8 & \text{secret number} & n=6 \\ \text{number n of their own.} & & & \\ \text{Each calculates } g^n \bmod p & 3^{8} \bmod 17=16 & & 3^{6} \bmod 17=15 \\ \text{They then exchange these} & A=16 & & B=15 \\ \text{resulting values.} & B=15 & & A=16\\ \text{Each then raises the value} & B^{n} \bmod p= & \text{mix in secret} & A^{n} \bmod p=\\ \text{they received to the power of } & & \text{number} & \\ \text{their secret }n \bmod p & 15^{8} \bmod 17=1 & & 16^{6} \bmod 17=1\\ \text{The result is the shared secret key.} & 1 & \text{shared secret key} & 1 \end{array}\)
Спільні секрети виходять однаковими через модульне правило потужності експоненти
\(\left(a^{b} \bmod n\right)^{c} \bmod n=\left(a^{c} \bmod n\right)^{b} \bmod n .\)Аліса обчислюється,\(\left(3^{6} \bmod 17\right)^{8} \bmod 17\) поки Боб
обчислив,\(\left(3^{8} \bmod 17\right)^{6} \bmod 17,\) що правило говорить, дасть ті ж результати.
Зверніть увагу, що навіть якщо снупер повинен був отримати обидва обмінені цінності\(B=15\),\(A=16\) і вони не можуть отримати спільний секретний ключ від них, не маючи принаймні одного з секретних номерів Аліси або Боба. Немає простого способу отримати секретні числа із загальних значень, оскільки функція була односторонньою функцією.
Використовуючи цей підхід, Аліса та Боб тепер можуть використовувати спільний секретний ключ, отриманий як ключ для стандартного алгоритму шифрування, такого як DES або AES.
Припустимо, ви робите обмін ключами з Кайлі, використовуючи генератор 5 і прайм 23. Ваш секретний номер - 2. Який номер ви надсилаєте Кайлі? Якщо Кайлі надсилає вам значення 8, визначте спільний секретний ключ.
- Відповідь
-
Щоб обчислити число, яке ми надішлемо Кайлі, ми піднімаємо генератор до потужності нашого модуля секретного числа простого:\(5^{2} \bmod 23=25 \bmod 23=2\).
Якщо Кайлі надсилає нам значення,\(8,\) ми визначаємо спільну таємницю, підвищуючи її число до сили нашого модуля секретного числа простим:\(8^{2} \bmod 23=64 \bmod 23=18.18\) був би загальним секретом.
РСА
Існує кілька інших методів відкритого ключа, включаючи RSA, який дуже часто використовується. RSA передбачає розповсюдження відкритого ключа шифрування, який кожен може використовувати для шифрування повідомлень до вас, але який можна розшифрувати лише за допомогою окремого приватного ключа. Ви можете думати про це як надсилання комусь відкритого замка - вони можуть заблокувати інформацію, але ніхто не може розблокувати її без ключа, який ви зберігали в таємниці.
Безпека RSA спирається на складність факторингу великих чисел. Наприклад, легко обчислити, що 53 рази 59 дорівнює 3127, але враховуючи число 12,317, що є добутком двох простих чисел, набагато складніше знайти числа, які множаться, щоб дати це число. Це експоненціально складніше, коли прості числа мають 100 або більше цифр. Припустимо, ми знаходимо два простих числа\(p\) і\(q\) і множимо їх, щоб отримати\(n=p q\). Це число буде дуже важко врахувати. Якщо ми також знаємо\(p\) і\(q\), є ярлики, щоб знайти два числа\(e\) і\(d\) так\(m^{e d} \bmod n=m \bmod n\) для всіх чисел\(m\). Не знаючи факторизації\(n\), знайти ці значення дуже важко.
Щоб використовувати RSA, ми генеруємо два простих числа\(p\) і\(q\) і множимо їх, щоб отримати\(n=p q\). так як ми знаємо факторизацію, ми можемо легко знайти\(e\) і\(d\) тому\(m^{e d}=m \bmod n .\) Тепер, ми\(d .\) замикаємо\(p\)
\(q,\) і потім ми відправляємо значення\(e\) і \(n\)публічно. Щоб зашифрувати повідомлення\(m,\) відправник обчислює\(S=m^{e} \bmod n .\) Як ми бачили раніше, модуль є односторонньою функцією, яка робить оригінальне повідомлення дуже важко відновити\(S\). Однак у нас є приватний ключ,\(d\) який ми можемо використовувати для розшифрування повідомлення. Коли ми отримуємо секретне повідомлення\(S\), ми обчислюємо\(S^{d} \bmod n=\left(m^{e}\right)^{d} \bmod n=m^{e d} \bmod n=m \bmod n,\) відновлення вихідного повідомлення [4].
Припустимо, що Аліса обчислила\(n=3127, e=3,\) і\(d=2011 .\) Покажіть, як Боб зашифрує повідомлення 50 і як Аліса потім розшифрує його.
Рішення
Боб знав би лише своє повідомлення\(m=50\) та відкритий ключ Аліси:\(n=3127\) і\(e=3 .\) Він шифрував би повідомлення шляхом обчислення\(m^{e} \bmod n: 50^{3} \bmod 3127=3047\)
Потім Аліса може розшифрувати це повідомлення, використовуючи свій приватний ключ,\(d\) обчислюючи\(S^{d}\) мод\(n\):
\(3047^{2011} \bmod 3127=50\)
Цей метод відрізняється від Diffie-Hellman-Merkle тим, що не потрібен процес обміну; Боб міг надіслати Алісі зашифроване повідомлення за допомогою відкритого ключа Боба без необхідності попередньо спілкуватися з Алісою, щоб визначити спільний секретний ключ. Це особливо зручно для таких програм, як шифрування електронної пошти, де обидві сторони можуть не бути в Інтернеті одночасно, щоб виконати обмін ключами в стилі Діффі-Хеллмана-Меркла.
[1] uk.wikipedia.org/w/index.php?... nge.svg&сторінка=1
[2] Відеоогляд цього процесу див. http://www.youtube.com/watch?v=YEBfamv-_do
[3] Колись замість того, щоб бачити 17 мод 5 = 2, ви побачите 17 ≡ 2 (мод 5). ≡ Символ означає «конгруентний» і означає, що 17 і 2 еквівалентні, після того, як ви вважаєте модуль 5.
[4] Багато деталей було залишено поза увагою, включаючи те, як визначаються e та d, і чому це все працює. Трохи докладніше див. http://www.youtube.com/watch?v=wXB-V_Keiu8 або http://doctrina.org/How-RSA-Works-With-Examples.html